千年第一定理——勾股定理

文/李明凯

一、勾股定理的历史

在公元前约三千年的古巴比伦人就知道和应用勾股定理，他们还知道许多勾股数组。美国哥伦比亚大学图书馆内收藏着一块编号为“普林顿322”的古巴比伦泥板，上面就记载了很多勾股数。古埃及人在建筑宏伟的金字塔和尼罗河泛滥后测量土地时，也应用过勾股定理。在中国公元前十一世纪，周朝数学家就提出“勾三、股四、弦五”;《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩，勾广三，股修四，经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时，径隅 (就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。

在西方公元前六世纪，希腊数学家毕达哥拉斯 (Pythagoras)证明了勾股定理，因而西方人都习惯地称这个定理为毕达哥拉斯定理。据说毕达哥拉斯发现了这个定理后，即斩了百头牛作庆祝，因此又称“百牛定理”。公元前4世纪，希腊数学家欧几里得 (Euclid，公元前330～公元前275)在巨著《几何原本》(第Ⅰ卷，命题47)中给出一个很好的证明。1876年4月1日，加菲尔德在《新英格兰教育日志》上发表了他对勾股定理的一个证法 (详见加菲尔德证法)。1940年《毕达哥拉斯命题》出版，收集了367种不同的证法。

二、勾股定理的验证推导

1、标准验证:该证明对切即为加菲尔德的梯形证明法

如右图所示:大正方形的面积等于中间正方形的面积加上四个三角形。

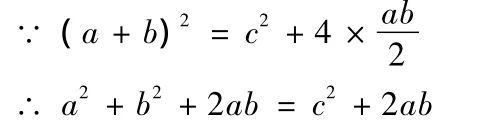
图示

2、毕达哥拉斯定律

任何一个学过代数或几何的人，都会听到毕达哥拉斯定理。这一著名的定理，在许多数学分支、建筑以及测量等方面，有着广泛的应用。古埃及人用他们对这个定理的知识来构造直角。他们把绳子按3，4和5单位间隔打结，然后把三段绳子拉直形成一个三角形。他们知道所得三角形最大边所对的角总是一个直角。毕达哥拉斯定理;给定一个直角三角形，则该直角三角形斜边的平方，等于同一直角三角形两直角边平方的和。反过来也是对的;如果一个三角形两边的平方和等于第三边的平方，则该三角形为直角三角形。

3、加菲尔德证法

加菲尔德在证出此结论5年后，成为美国总统，所以人们又叫它总统定理。

在直角梯形ABDE中，∠AEC=∠CDB=90°，△AEC≅△CDB，

AE=CD=b，AE=BD=a，AC=BC=c

三、勾股定理定理推广和运用的意义

1、逆定理

勾股定理逆定理:如果三角形三边长a，b，c满足a^2+b^2=c^2，那么这个三角形是直角三角形。

勾股定理的逆定理是判断三角形为钝角、锐角或直角的一个简单的方法 (依据)，其中C为最长边:

如果a2+b2=c2，则△ABC是直角三角形。如果a2+b2＞c2，则△ABC是锐角三角形。(若无先前条件C为最长边，则仅满足∠C是锐角)

如果a2+b2＞c2，则△ABC是钝角三角形。

2、推广定理

欧几里得在他的《几何原本》中给出了勾股定理的推广定理:“直角三角形斜边上的一个直边形，其面积为两直角边上两个与之相似的直边形面积之和”。

利用勾股定理求线段长度这是勾股定理的最基本运用，通常是在一个直角三角形中，已知两条边的长度，求第三边。对于这类问题，可以直接代入公式进行计算，比较容易。

3、勾股定理意义

它是几何学中的明珠，它充满魅力，千百年来，人们对它的证明趋之若鹜，其中有著名的数学家、画家，也有业余数学爱好者，有普通的老百姓，也有尊贵的政要权贵，甚至有国家总统。也许是因为勾股定理既重要又简单又实用，更容易吸引人，才使它成百次地反复被人炒作，反复被人论证。1940年出版过一本名为《毕达哥拉斯命题》的勾股定理的证明专辑，其中收集了367种不同的证明方法。实际上还不止于此，有资料表明，关于勾股定理的证明方法已有500余种，仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。这是任何定理无法比拟的

勾股定理作为一个被人类早期发现并证明的重要数学定理之一，对数学的发展产生了不可小视的影响。勾股定理使人们以代数的思想与概念来解决几何问题，正是“数形结合”思想的体现，这样的思想角度是十分重要的。同时，勾股定理的发现推动了人类对数学几何更深的探索;通过勾股定理，我们可以推导出许多其它真命题与定理，这大大地方便了我们对几何问题的解决，也使数学的发展迈出了一大步。