基于聚类混合遗传算法的LRP问题研究

柴宏建 ， 高尚策

（1.东华大学 信息科学与技术学院，上海 201620；2.数字化纺织服装技术教育部工程研究中心 上海 201620）

物流作为“第三利润”的源泉，近年来逐渐成为众多企业、专家和学者的研究热点。物流网络的日趋复杂，以及交通条件的日益改善其地理分布也不断扩大，导致物流网络优化的各个子问题（物流中心选址问题、车辆配送路径问题等）之间的相互影响也越来越大。单纯的中心选址问题在建设物流中心时只考虑运输车辆从中心到需求点的射线型运输方式，忽略了对车辆配送路径进行优化，必然导致运输成本的增加；而车辆配送路径问题只考虑了配送车辆在各需求点之间依次进行配送，虽然对路径进行了优化，提高了运输效率，但由于缺乏对物流中心选址问题的考虑，使得整个物流 网络的成本仍不能降到最低。现实中将中心选址问题和配送路径优化问题放在一起进行综合考虑，逐渐形成了选址-配送联合优化问题（Location-Routing problem，LRP）。 Tai-His Wu[1]等人将LRP问题分解为LAP和VRP两个子问题分别进行求解。Wang，Xuefeng[2]等人运用两阶段混合启发式搜索方法对LRP进行了求解，Maria Albareda[3]等人研究了随机 LRP问题，并建立了两阶段模型，提出了两阶段启发式算法和下界求法。

本文将配送中心选择与配送路径优化问题同时考虑，通过聚类算法[6]将需求点划分为适当的区域，然后针对每个区域，运用改进的混合遗传算法对车辆巡回线路进行优化，克服了传统遗传算法的易陷入局部收敛的缺陷，求得总体成本最小的优化方案。

1 模型建立

1.1 LRP定义

LRP可以表述为:给定一系列候选设施及其位置，在一定时间段内每个客户需求仅由某个确定的设施点出发的车辆来服务，在满足一定的约束条件下，以总配送成本最低为目标函数，确定开放设施的位置及数量，并确定车辆最佳的运输行程路线。其总费用包括设施的建设成本、运输成本以及车辆使用成本等。

本文研究LRP模型基于的假设：客户量、位置及需求已知；候选设施位置及容量已知；各客户需求均能得到满足且每个客户只由一辆车服务；每辆车在完成全部运输任务回到出发点，各线路的总需求小于或等于车辆的容量，车辆类型给定。

1.2 模型参数及决策变量

G={r|r=1，2，…，R}为 R 个候选设施点集合；H={i|i=R+1，R+2，…，R+N}为 N 个客户点集合；S={G}∪{H}为所有候选设施点及客户点集合；V={k|k=1，2，…，K}表示车辆集合；dij表示i到j的两点间的距离；C0表示单位距离运输成本；Ck表示车辆k的使用成本（k∈V）；Fr为设施r开放及运作的平均成本（r∈G）；Qr为设施 r的容量（r∈G）；qj为客户 j的平均需求量（j∈H）；Qk为车辆的容量 （k∈V）；Uik表示客户 i在路线 k 上被访问的次序（i∈H，k∈V）。

决策变量：

1.3 LRP 模型

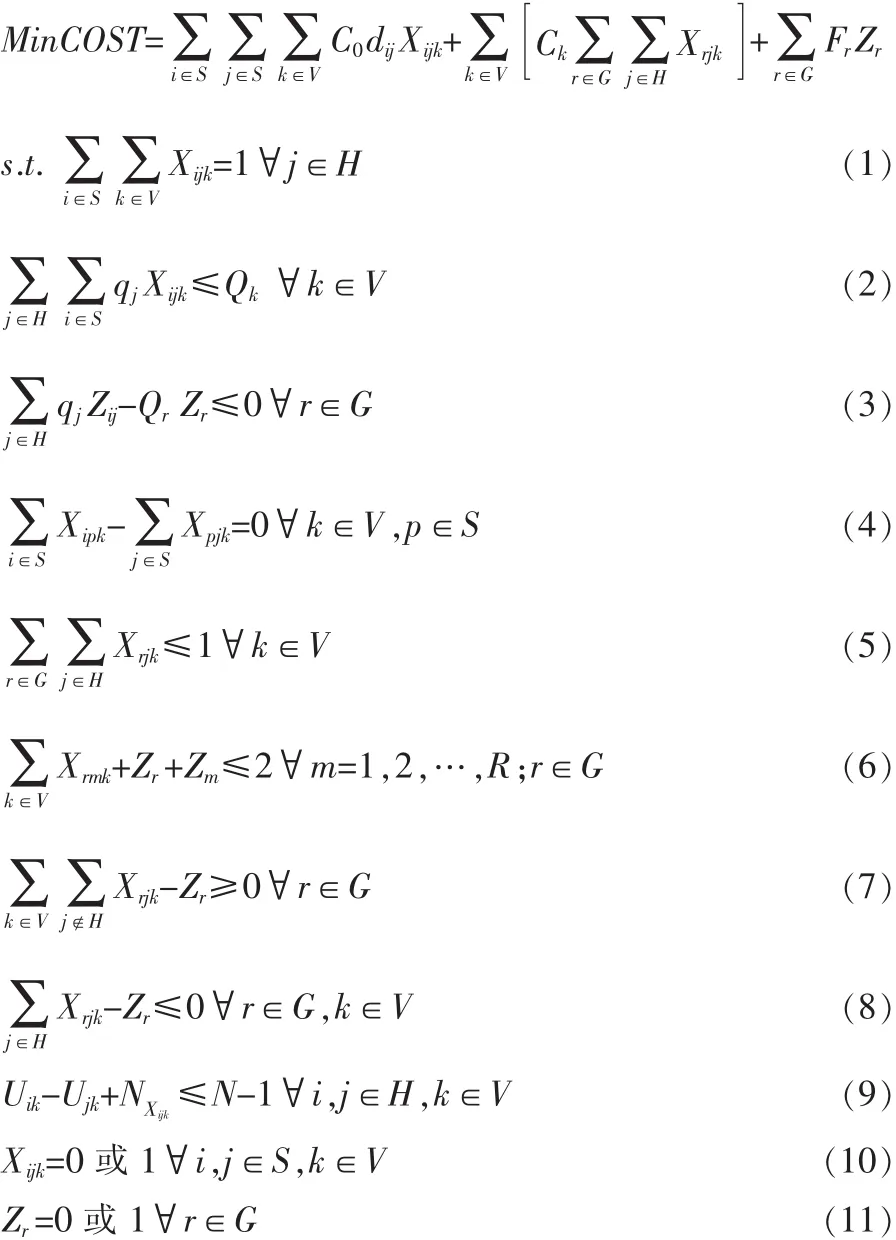
模型的目标函数为总成本最小 （总成本包括车辆使用成本、运输成本及设施建设成本）。约束条件：1）式确保每个客户仅由一车辆提供服务；2）式为车辆容量约束，确保车辆承担的客户总需求不超过车辆容量；3）式为设施约束；4）式为车辆路线连续性约束；5）式确保每辆车只为一个设施服务；6）表示任意两设施相互独立；7）式保证任意开放设施必须有车辆为其服务；9）式为支路消去约束，保证任意路线中含有一个设施；式（10）和式（11）为（0，1）变量约束。

2 算法设计

将物流配送中心及配送路径两方面的优化问题结合在一起进行考虑，建立的双层规划模型具有NP-Hard的性质，用一般的运筹学方法无法解决。因此，在对其进行求解时，一般会分为两个阶段进行求解，先寻求优化模型其中一个层次的最优解，带入模型的另一个目标函数，从而得出整个模型的最优化方案。本文设计基于聚类算法及遗传算法的两阶段混合式算法，并根据实际问题中的不同决策变量，对模型进行求解。

在求解的第一阶段先用聚类算法对最优选址问题进行求解，并根据第一阶段求解得到的物流中心选址，在第二阶段利用遗传算法对各物流中心负责配送的需求点进行配送路径安排，通过不断的迭代实现两阶段之间的协调优化。求解的具体算法流程如图1所示。

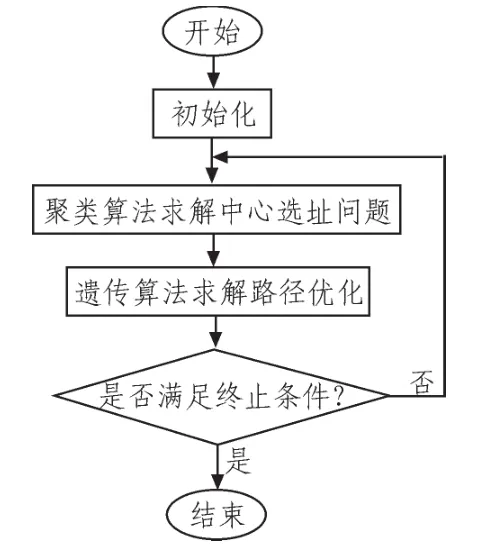
图1 双层规划模型求解算法设计图Fig.1 Flowchart of algorithm design for bilevel programming model

2.1 聚类算法求解上层模型

K-means算法是硬聚类算法，是典型的基于原型的目标函数聚类方法的代表，它是数据点到原型（类别中心）的某种距离和作为优化的目标函数，利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似性测度，它是求对应某一初始聚类中心向量 V=（v1，v2，…，vk）T最优分类，使得评价指标Jc值最小。算法常采用误差平方和准则函数作为聚类准则函数，误差平方和准则函数定义为：Jc=其中，Mi是类Ci中数据对象的均值，p是类Ci中的空间点。

分析误差平方和准则函数发现：K-means算法是一个最优化求解问题，目标函数存在着许多局部极小点，只有一个全局最小点。目标函数的搜索方向总是沿着误差平方和准则函数减小的方向进行。K-means算法采用迭代更新的方法：在每一轮迭代中，依据k个聚类中心将周围的点分别组成k个簇，而重新计算的每个簇的质心（即簇中所有点的平均值）将被作为下一轮迭代的参照点。迭代使得选取的参照点越来越接近真实的簇质心，所以目标函数越来越小，聚类效果越来越好。具体的算法流程图如图2所示。

图2 聚类算法流程图Fig.2 Flowchart of clustering algorithm

2.2 遗传算法求解下层模型

经典的物流配送路径优化问题（VRP）[5]是典型的组合优化问题，属于一类NP完全难问题，具有较高的计算复杂性。它只考虑了少量的约束条件，与现实问题比起来，还过于简单，还不能很好的模拟实际情况.为了更贴近实际情况，车辆路径问题（VRP）可以扩展成多中心车辆路径问题（MDVRP）。求解配送路径优化问题的方法很多，常用的有动态规划法、节约法、扫描法、分区配送算法，方案评价法等。

遗传算法本质上是一种不依赖具体问题的直接搜索方法，具有较强的问题求解能力和较强的鲁棒性，能够解决非线性优化问题。因此遗传算法在物流配送领域越来越受重视。

爬山算法是一种基于邻域搜索技术的、沿着有可能改进解的质量的方向进行的单方向搜索的搜索方法。本文尝试将爬山算法与自适应遗传算法相结合，能有效克服传统遗传算法易陷入局部极小的问题，收敛速度更快。

2.2.1 编码设计

编码是实现问题解空间到遗传编码的转换过程。根据物流配送路径优化问题的特点，我们采用直接排列的编码方法，该方法直接生产N个1~N间的互不重复的自然数的排列，即构成一个个体，按照约束条件依次将个体中的元素（客户）归入各配送路径中。

2.2.2 适应度评估

本文根据上文所确定的编码方法，适应度函数的确定要同时反映解的可行性与对应方案的费用。对于个体r，设其对应的配送路径方案的不可行路径数为Mr（Mr=0表示该个体对应一个可行解），目标函数值为COSTr，则该个体r的适应度函数Fr表示为：

其中，pW为每条不可行路径的惩罚函数 （该权重可以取目标函数取值范围中的一个相对较大的正数）。

2.2.3 改进的自适应交叉和变异操作

交叉和变异概率是影响遗传算法性能的两个重要的参数.Srinvivas[6]最早提出了一种自适应遗传算法，在该算法中，交叉概率Pc和变异概率Pm的值能够随着种群中个体的适应度值的大小来进行自动改变。但是该改进GA在进化初期并不理想，容易陷入局部最优。在Srinvivas自适应遗传算法的基础上我们采用一种典型方法控制两个参数:

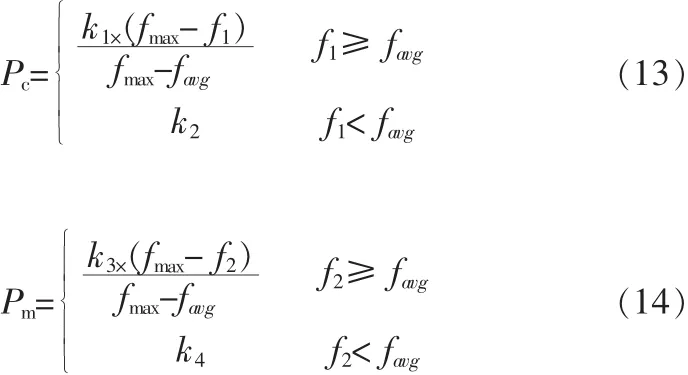
式中，k1，k2，k3，k4是（0，1）之间的常数。 从公式（13）、（14）可知，当个体的适应度值等于最大适应度时，其交叉和变异概率为0，则算法的进化能力会受到限制，所以本文在该自适应算法的基础上提出一种新的自适应交叉和变异概率，如公式（15）、（16）。当个体适应度值等于最大适应度值时，也可按一定的概率进行交叉和变异操作，从而提高了算法的寻优能力，更易跳出局部最优。

其中：f1为要交叉的两个个体中的较大适应度值，f2是要变异个体的适应度值，favg每代群体的平均适应度，fmax为群体中的最大适应度值。Pc1为初始交叉概率，Pm1为初始变异概率。

交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。具体操作为：

Step1:按照自适应交叉概率从种群中选择两个个体，称为父个体 P1，P2。

Step2:其次在父代P1，P2中选取两个非空互余子集D1，D2。

Step3:选取P1中属于D2的基因组成新的基因片段H1，取P2中属于D1的基因组成新的基因片段H2填入到基因片段H1相应的位置得到子代C1。

Step4:同理，选取P2中属于D2的基因组成新的基因片段G2，取P1中属于D1的基因组成新的基因片段G1填入到基因片段G2相应的位置，得到子代C2。

Step5:在生成的两个子代个体C1、C2与父代个体P1、P2组成的4个个体中，比较其适应度值；当两个子代中具有最大适应值的个体大于或等于父代中具有最大适应值的个体时，认为子代优于父代，将子代替换父代；否则，保留父代，让其入下一轮的进化。

利用改进的自适应交叉方法进行交叉运算，不会产生不合理的染色体表现型，可以提高算法的搜索能力和种群的多样性，有效地避免了算法陷入局部最优的情况。

交叉操作之后，我们利用自适应的变异方法处理上一步得到的种群，首先随机选择一个父代，然后再随机生成两个整数a1和 a2（a1，a2∈[1，n×m]），最后交换父代中 a1和 a2位置上的基因。

2.2.4 爬山操作

针对遗传操作产生的每代群体的最优个体，通过邻域搜索实施爬山操作。本文采用基因换位算子实现爬山操作，具体步骤如下：

1）在个体中随机选择两个基因，交换其位置；

2）判断基因换位后的适应值变化，若适应值增加，则用新个体取代原个体；

3）重复 1）、2），直至达到一定交换次数。本文算法流程如图3所示。

图3 改进的算法流程图Fig.3 Flowchart of improved algorithm

3 实验及仿真结果

为了分析此混合遗传算法的可行性及有效性，我们配置的仿真环境是：Windows 7操作系统，Intel（R）Core i5 CPU 2.40 GHz，2 GB内存，Matlab R2009b编译软件，采用数据随机生成的方法，在均匀分布二维区间[0，100]2中随机产生各需求点的坐标（xi，yi），各需求点的需求 qi在均匀分布区间[1，50]2中随机产生，中心个数设为3。根据本文算法求得的聚类中心和最终车辆数目及优化线路分别如图4和图5所示。

4 结束语

本文分析了物流选址及配送路径模型，通过聚类分析的方法，根据成本最小化将各需求点分配到不同的区域，分别由多个配送中心服务；然后运用改进的遗传算法很好的解决了每个区域配送中心的配送路径优化问题，使之更贴近实际，并编写了相应的程序通过数值试验验证了此方法的有效性与优越性。本文的MDVRP中，没有涉及应对动态信息的处理方法，在现实物流配送过程中，配送车辆被派出后，客户可能会变更订单，或者出现预定路线被阻断等突发事件，在下一步的工作中，希望能解决这些问题。

图4 中心选址结果图Fig.4 The figure of center location results

图5 最终车辆路径线路图Fig.5 The figure of final vehicle road

[1]Tai-His Wu，Chinyao Low，Jiunn-Wei Bai.Heuristic solutions to multi-depot location-routing problems[J].Computer&Operation Research，2002（29）:1392-1417.

[2]WangXuefeng，SunXiaoming，FangYang.A two-phase hybrid heuristic search approach to the location-routing problem（C）.ConferenceProceedings-IEEE International Conference on Systems， Man and Cybernetics，2005:3338-3343.

[3]Albareda-Sambola M，Fernández E，Laporte G.Heuristic and lower bound for a stochastic location-routing problem[J].European Journal of Operational Research，2007，179 （3）:940-955.

[4]Barreto S，Ferreira C，Paixao J，et al.Using clustering analysis in acapacitated location-routingproblem[J].European Journal of Operational Research，2007，179（3）:968-977.

[5]Chen Haijun，Chen Yieyin.Application of Hybrid Genetic Algorithm in Vehicle Routing Problem[J].Commputer&Digital Engineering，2005，33（4）:91-95.

[6]Srinivas M，Patnaik L M．Adaptive probabilities of crossover and mutation in genetic algorithms[J]．IEEE Transactions on Systems，Man and Cybernetics，1994，24（4）:17-26.