载人航天器主动热控系统热负荷布局优化

彭 灿，徐向华，梁新刚

(清华大学航天航空学院，热科学与动力工程教育部重点实验室，北京100084)

0 引言

热控系统是载人航天器的重要组成部分。为了给航天员提供舒适的工作和生活环境以及保证各种设备正常工作，热控系统需要将航天员和设备产生的废热排散到太空环境中去。热控系统可以分为被动热控系统和主动热控系统［1］。主动热控系统因具有控制能力强，能够适应极端温度条件等特点［1］而应用广泛。目前人类发展的载人航天器普遍采用以单相流体回路为主的主动热控系统，如“国际空间站”、“神舟”飞船等。通常载人航天器主动热控制系统包括内部热控制系统和外部热控制系统［2］，内部热控系统还可以分为低温内回路和中温内回路，分别提供温度不等的冷源。航天器密封舱内的热负荷分别布置在低温内回路和中温内回路上，由于回路温度水平不同，热负荷在内回路上的布局会影响相应换热器的换热面积，进而影响整个热控系统的质量。

为了满足热控要求，航天器的热控系统通常非常复杂因而质量较大，而航天器的发射费用又极为昂贵，所以在满足热设计要求的前提下，减小热控系统的质量具有非常重要的意义。众多的研究者对热控系统的轻量化进行了研究。Mark等［3］提出空间站B阶段热控系统的设计应该以轻量化为目标。Gianfiglio等［4］在Hermes航天飞机的设计中提出应综合考虑热控系统的重量、安全性和可靠性。Claudio等［5］则进一步指出Hermes航天飞机的热控系统各个组件(如换热器、冷板、阀门、管路等)的选型和设计都应该以轻量化为原则。徐向华等［6］提出了将热控系统轻量化设计转化为以系统质量最小为目标的约束优化问题的设计思路。李明海等［7］从轻量化设计角度提出热泵－蓄冷组合热控方案。张信荣等［8－9］建立了载人航天器热网络系统的物理数学模型，分析了总换热面积最小的冷媒分配原则，并对简单串联热组件的布局进行了优化研究。程雪涛等［10］采用Lagrange乘子法对并联换热网络进行了分析，得到了最佳冷流体分配系数。Zhou等［11］则进一步将Lagrange乘子法应用到双回路主动热控系统的全局轻量化研究中。但对于热负荷应该布置在低温内回路还是中温内回路的选择原则尚未见到报道。

本文将对一定温度的热负荷在热控系统流体回路中的布局进行讨论。在给定的约束条件下参考文献［11］给出的方法进行求解，比较热负荷布置在低温内回路和中温内回路两种方案整个热控系统流体回路总质量。给出一定温度和功率的热负荷的布置原则，并从流体回路换热温差的分配角度给出直观的定性分析，从而为热控系统流体回路的轻量化设计提供一定参考。

1 主动热控系统流体回路方案介绍

本文针对一典型的载人航天器主动热控系统流体回路进行讨论，根据热负荷位置的不同，流体回路系统框图分别如图1和图2所示。流体回路包括低温内回路、中温内回路和外回路。低温内回路和中温内回路采用水作为工质，外回路为了避免结冰而采用全氟三乙胺作为工质。低温内回路工作在较低的温度，为了保证空气中的水蒸气能冷凝除湿，换热器水侧入口温度Tl1设为定值。中温内回路主要用于冷却系统设备，工作温度相对较高。为了简化问题，流体回路中的主要设备抽象成3个换热器、2个冷板和1个辐射器。乘员舱中的空气通过换热器HEl向低温内回路传递热流Ql，换热器空气侧入口温度为Tl0。温度为Tm0功率为Qm的热负荷通过与中温内回路的冷板连接向流体回路散热。低温内回路和中温内回路流体将收集的热量通过两个中间换热器HEe1和HEe2传递给外回路流体，最后通过外回路上的辐射器HEr散发到太空中去。太空的等效的辐射热沉温度为Ts，辐射器表面温度Tr视为均匀。温度为Tx功率为Qx的热负荷通过与冷板HEx连接向流体回路散热。图1所示为方案1，热负荷Qx布置在低温内回路;图2所示为方案2，热负荷Qx布置在中温内回路。本文对这两种方案分别进行以系统总质量为目标的优化分析，比较这两种方案的优劣。

图1 Q x布置在低温内回路流体回路系统Fig．1 Fluid loop system with the heat load arranged in low-temperature internal loop

2 主动热控系统流体回路的数学模型

以方案1为例对主动热控系统流体回路的数学模型进行说明，方案2用同样的方法进行计算。主动热控系统流体回路总质量包括换热器、冷板、辐射器、管道及工质、驱动流体循环的泵及其所需要的电源系统。

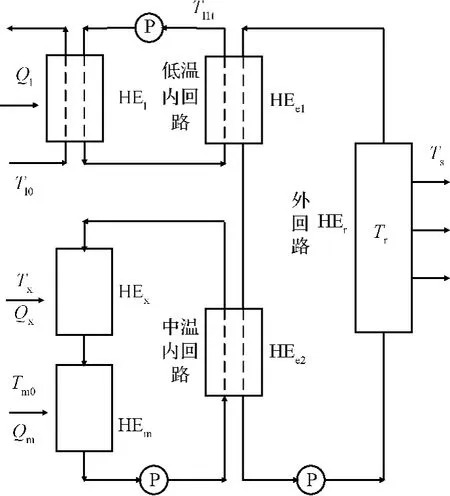
图2 Q x布置在中温内回路流体回路系统Fig．2 Fluid loop system with the heat load arranged in middle-temperature internal loop

流体回路中换热器和冷板的总质量为［12］:

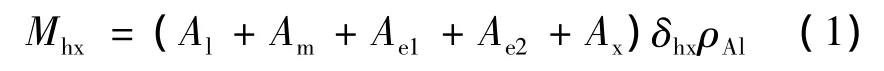
式中:Al、Ae1、Ae2、Am和Ax分别为换热器HEl、HEe1和HEe2，冷板HEm和HEx的换热面积，δhx为换热器和冷板换热面的厚度，换热器和冷板的材料为铝，ρAl为铝的密度。

辐射器的质量为［12］:

式中:Ar为辐射器HEr的面积，φ为辐射器单位面积的质量。

管道和管道中工质的质量分别为:

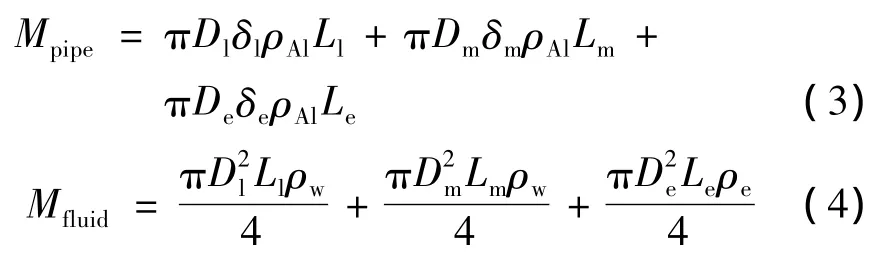
式中:D、L和δ分别表示管径、管长和管道壁厚，下标l、m和e分别表示低温内回路、中温内回路和外回路参数。式中ρw和ρe分别为水和全氟三乙胺的密度。

流体通过管道时压损为［13］:

式中:f为管道中流体的阻力系数，层流时f=64/Re，湍流时f=(1．82lg Re－1．64)－2［14］，Re为雷诺数，g体现弯头或者三通的影响，n为管道弯头或者三通的数量。

流体通过换热器时压损采用等效长度Lhx来表示:

等效长度参考中小型空间站的尺寸估算得到。本文的计算工况(见表1)中低温内回路换热器的等效长度为25 m，中温内回路换热器的等效长度为25 m，外回路换热器的等效长度为30 m。该工况下管道中损失的压降占回路中总压降的30%左右。

泵功率为:

式中:q为质量流量，η为泵效率。

由式(5)～(7)可得整个流体回路消耗的泵功率为:

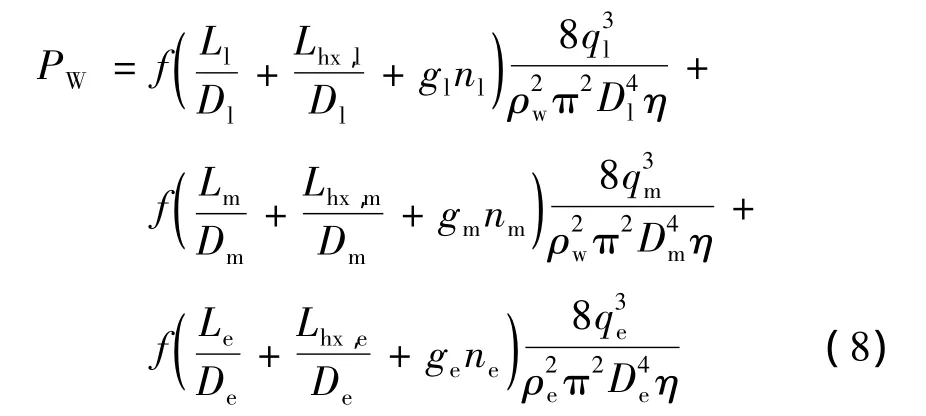
认为泵质量Mpump与功率为线性关系［12］:

式中:χ为比列系数，C为泵的基础质量。

设电源系统质量与功率满足如下关系［12］:

式中:e为电源质量比例系数。

流体回路的总质量为:

流体回路各部分的参数需要满足一定约束条件。

对于换热器有:

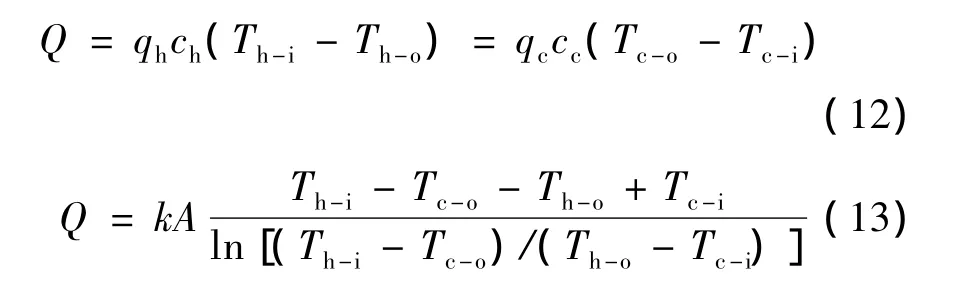
对于冷板有:

对于辐射器有:

式中:Q为热流量，q为质量流量，c为比热容，T为温度，下标h和c分别表示冷热流体，i和o表示换热器或冷板的进出口，Tr和Ts表示辐射器表面温度和太空的等效辐射热沉温度，ε为辐射器的发射率，σ为斯特藩－玻尔兹曼常数，A为换热面积，k为传热系数。

对于冷板传热系数［5］:

对于换热器传热系数:

式中:H为对流换热系数，B为比例系数，δ为换热器换热面厚度，λ为换热面材料导热系数，通常δ很小λ很大，所以换热面的导热热阻可以忽略不计，于是换热器的传热系数为:

在这些约束条件下，参考文献［11］给出的Lagrange乘子法对热控系统流体回路总质量进行分析。其中优化参数包括换热器面积Al、Ae1、Ae2、Am和Ax，管径Dl、Dm和De，质量流量ql、qm和qe，而辐射器的面积为给定值。

3 计算结果及分析

计算模型中选取的主要参数如表1所示。对于每一个给定的Tx利用文献［11］给出的Lagrange乘子法都可以得到一个系统最小质量。图3所示为Qx为900 W时方案1和方案2热控系统流体回路的总质量随Tx的变化。这里所说的总质量不包括辐射器的质量，因为本文优化计算过程中认为辐射器的质量不变。从图3可以看出存在一个临界温度Tx(记为Tx－e)使两种方案的总质量相等，Tx相对较低即小于Tx－e时方案1的总质量比方案2小，随着Tx增大两种方案质量的差别逐渐减小，在Tx相对较高即大于Tx－e时，方案1的总质量超过方案2。也就是说在本文研究范围内，为了使热控系统质量较小，Tx相对较低时热负荷Qx应该布置在低温内回路，Tx相对较高时热负荷Qx应该布置在中温内回路。

表1 主动热控系统流体回路主要参数Table 1 Main parameters of the active thermal control fluid loop

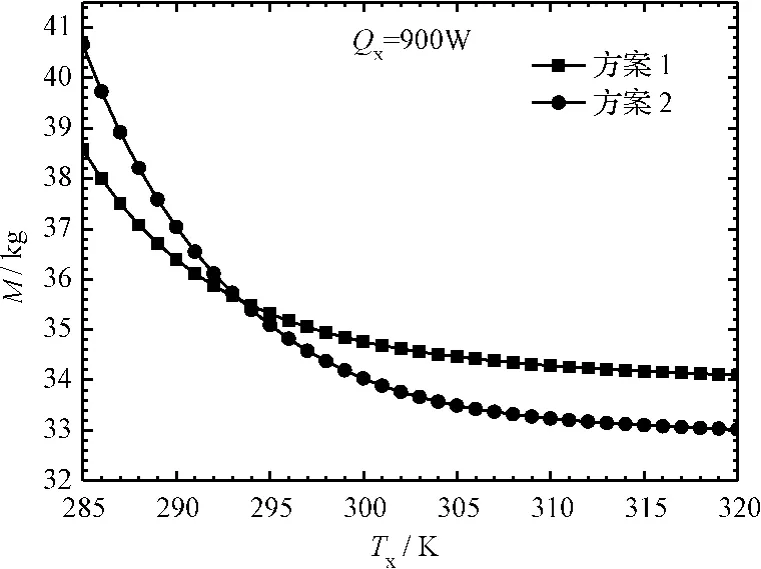
图3 方案1和方案2流体回路的总质量(不包括辐射器的质量)随T x的变化Fig．3 The variations of total system mass(mass of the radiator not included)with T x for case 1 and case 2

以上分析结论预示着热负荷的分布应尽量使得 传热温差分布均匀，不应出现某个传热环节的温差很大，而另外的环节温差很小的情况。为了进一步阐述这一规律，考虑一个简单的串联传热过程，给定的热流量Q0经过两个串联的换热器HE01和HE02，如图4所示。对应的对数平均温差分别为ΔT1和ΔT2;对应的热阻分别为R01和R02;对应的换热面积分别为A01和A02。根据传热关系式有:

式中:q为经过两个冷板的流量;c为流体的比热容;T1和T2分别为上下温度界限;Tm1和Tm2分别HE01入口和出口温度;k1和k2分别为HE01和HE02的换热系数。假设k1=k2，很容易证明，当:

此时ΔT1=ΔT2时，也即是说对数平均温差分布均匀时，两个换热器的换热面积之和最小。

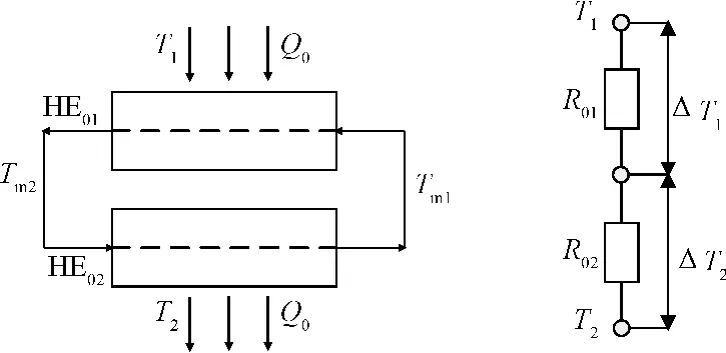
图4 简单串联传热过程示意图Fig．4 Sketch of the simple heat transfer process

那么对于本文讨论的主动热控流体回路，也应该使温差分布趋于均匀，避免温度较低的热负荷布置在中温内回路，而温度较高的热负荷布置在低温内回路。定性上，可从方案1和方案2系统的内外流体回路简化的温差分布示意图(如图5和图6所示)的角度进行分析(并且暂不考虑方案1和方案2回路中流量的变化对温差分布的影响)。图中ΔTx为热负荷Qx和与之进行换热的内回路之间冷板的对数平均温差，ΔTl为低温内回路与外回路之间换热器的对数平均温差，ΔTm为中温内回路与外回路之间换热器的对数平均温差，R1～R7表示流体回路各个换热环节的热阻。R1为辐射器与太空的辐射热阻，R2为外回路与辐射器的换热热阻，R3为换热器HEe1的换热热阻，R4为换热器HEe2的换热热阻，R5为换热器HEl的换热热阻，R6为冷板HEx的换热热阻，R7为冷板HEm的换热热阻。由于中温内回路的平均温度比低温内回路平均温度高，ΔTl比ΔTm小，因此方案1与方案2相比热负荷Qx布置在低温内回路时换热器HEe1增加的换热面积比布置在中温内回路换热器HEe2增加的换热面积大，但方案1的ΔTx比较大，因此冷板HEx的换热面积较小。当热负荷Qx的温度Tx较低时，随着Tx的降低，方案2的ΔTx会变得很小，而换热面积会增加较快。从传热关系式Q=kAΔT来看，当Q一定，换热面积A和对数平均温差ΔT成反比，所以当ΔT较小时，随着ΔT的减小换热面积A会迅速增加。因此当热负荷Qx的温度Tx较小时，方案2系统的总质量较大。当热负荷Qx的温度Tx增加时，方案2的ΔTx会增加，当ΔTx较大时，随着ΔTx的增加换热面积A减小得缓慢，因此冷板HEx布置在低温内回路与中温内回路换热面积的差别变小，而热负荷Qx布置在低温内回路时换热器HEe1增加的换热面积比布置在中温内回路换热器HEe2增加的换热面积大这一因素占主导，因此方案1的系统总质量较大。

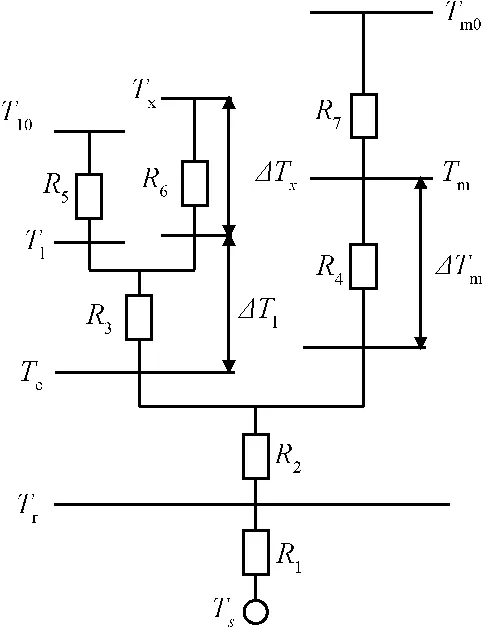
图5 方案1流体回路温差分布示意图Fig．5 The loop temperature difference distribution diagram of case 1

图6 方案2流体回路温差分布示意图Fig．6 The loop temperature difference distribution diagram of case 2

为了进一步验证上述结论，本文还对热负荷Qx和电源质量比例系数e取不同值的情况进行了计算，计算结果如图7和图8所示。结果显示，在本文的研究范围内，Qx和电源质量比例系数e取不同的值时，为了降低热控系统的质量，Tx较小时热负荷Qx应该布置在低温内回路，Tx较大时热负荷Qx应该布置在中温内回路的结论仍然是成立的。并且当Qx和e取不同值时，临界温度Tx－e也不同。

4 结论

本文对给定温度和发热功率的热负荷布置在低温内回路和中温内回路两种方案的主动热控系统流体回路的总质量进行了分析，讨论了热负荷的布置原则，从温差分配角度给出了直观的解释。结果表明:

1)热负荷应该放在低温内回路还是放在中温内回路与温度和发热功率都有关;

2)存在一个热负荷临界温度使两种方案流体回路系统的总质量相等，热负荷温度相对较低时布置在低温内回路可使系统的总质量较小，反之应当布置在中温内回路;

图7 不同Q x时方案1和方案2流体回路的总质量(不包括辐射器质量)随T x的变化Fig．7 The variations of total system mass(mass of the radiator not included)with T x for case 1 and case 2 at different heat loads Q x

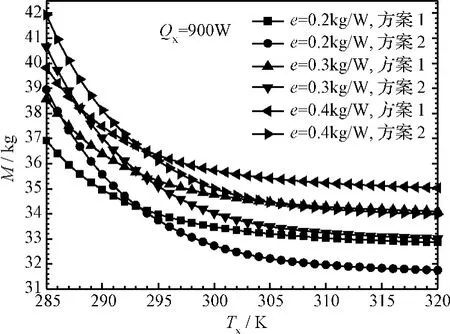
图8 不同电源质量比例系数e时方案1和方案2流体回路的总质量(不包括辐射器质量)随T x的变化Fig．8 The variation of total system mass(mass of the radiator not included)with T x for case 1 and case 2 at different power supply mass ratios e

3)对于串并联的流体回路，对于给定温度上下限的情况，各传热环节的温度选取应尽量使得各部分温差分布趋于均匀。

［1］ 侯增祺，胡金刚．航天器热控制技术［M］．北京:中国科学技术出版社，2007．

［2］National Aeronautics and Space Administration．International space station familiarization［R/OL］．［1998－7－31］．http://www．spaceref．com/iss/ops/iss．familiarization．pdf．

［3］Mark T H，David W P．Preliminary design of the space station internal thermal control sytem［J］．SAE Paper，1985，96(6):712－723．

［4］Gianfiglio G，Ferro C．Hermes thermal control system-a preliminary design［J］．SAE Paper，1988，97(1):288－304．

［5］Claudio F，Antonio M．Hermes thermal control subsystem–design concepts［J］．SAE Paper，1990，99(1):1066－1080．

［6］ 徐向华，程雪涛，梁新刚．载人航天器主动热控制系统流体回路的优化设计［J］．宇航学报，2011，32(10):2285－2293．［Xu Xiang-hua，Cheng Xue-tao，Liang Xin-gang．Design and optimization for fluid loops of active thermal control system in manned spacecraft［J］．Journal of Astronautics，2011，32(10):2285－2293．］

［7］ 李明海，任建勋，梁新刚，等．航天器热控系统中的热泵－蓄冷组合方案［J］．宇航学报，2002，23(2):1－5．［Li Ming-hai，Ren Jian-xun，Liang Xin-gang，et al．An integrated heat pump-ice thermal storage scheme for thermal control system of spacecraft［J］．Journal of Astronautics，2002，23(2):1－5．］

［8］ 张信荣，任建勋，梁新刚，等．载人航天器并联热网络系统的优化分析［J］．清华大学学报(自然科学版)，2002，42(4):462－465．［Zhang Xin-rong，Ren Jian-xun，Liang Xingang，et al．Optimization of the thermal network in parallel connection of manned spacecraft［J］．Journal of Tsinghua University(Scince and Technology)，2002，42(4):462－465．］

［9］ 张信荣，任建勋，梁新刚，等．载人航天器环控生保系统热网络质量的优化［J］．清华大学学报(自然科学版)，2000，40(4):47－50．［Zhang Xin-rong，Ren Jian-xun，Liang Xingang，et al．Mass optimization of thermo-hydraulic network of manned spacecraft environment control and life support system［J］．Journal of Tsinghua University(Scince and Technology)，2000，40(4):47－50．］

［10］ 程雪涛，徐向华，任建勋，等．用Lagrange乘子法优化并联液体冷却网络系统［J］．清华大学学报(自然科学版)，2008，48(8):1359－1361，1367．［Cheng Xue-tao，Xu Xiang-hua，Ren Jian-xun，et al．Optimization of liquid cooling networks with couple parallel connections using Lagrange multipliers［J］．Journal of Tsinghua University(Scince and Technology)，2008，48(8):1359－1361，1367．］

［11］Zhou B，Cheng X T，Liang X G．Conditional extremum optimization analyses and calculation of the active thermal control system mass of manned spacecraft［J］．Applied Thermal Engineering，2013，59(1－2):639－647．

［12］ 张信荣．空间站环控生保系统热管理研究［D］．北京:清华大学，2002．［Zhang Xin-rong．Thermal management of environment control and life support system of space stations［D］．Beijing:Tsinghua University，2002．］

［13］Yamaguchi H．Engineering fluid mechanics［M］．Springer Netherlands，Kyoto，2008．

［14］ 杨世铭，陶文铨．传热学［M］．北京:高等教育出版社，2006．