一种聚类后排序的灰色聚类评价方法

李志亮，罗 芳，阮群生

（宁德师范学院计算机系，福建宁德352100）

一种聚类后排序的灰色聚类评价方法

李志亮，罗 芳，阮群生

（宁德师范学院计算机系，福建宁德352100）

在灰色聚类分析法的基础上，改进传统的白化权函数，并对聚类后的评价对象进行排序，进而构建一个聚类后排序的灰色聚类评价方法.新的评价方法不仅可以对评价对象进行聚类，而且对同一灰类的评价对象进行排序，较好地解决了聚类对象的聚类和排序问题.引用图书馆员实际数据分析说明，构建的灰色聚类评价方法能够有效避免图书馆员工作评价的盲目性，为图书馆员的选拔、聘任和评价提供量化依据.

灰色聚类；排序；灰类；工作评价

高校图书馆是大学生获取课外信息的重要来源.图书馆员作为图书馆主要功能的实行者，其素质的高低和服务质量的好坏对图书馆各项功能的发挥有着重要的影响.合理评价图书馆员的工作，有利于充分调动广大图书馆员的工作积极性，提高图书馆员素质，进而更好地为学生服务.

灰色系统理论[1]主要用于解决含未知因素的问题，灰色聚类法作为其重要组成部分被广泛用于水、大气、土壤环境质量评价[2-4]，证券投资分析[5]，区域经济实力评价[6]等.近几年，许多学者将灰色聚类法应用于高校教学方面[3,7]，通过灰色聚类法构造白化权函数，计算聚类对象的差异性来分析和建立评价模型.基于中心点三角白化权函数能够方便、快捷地划分每个对象所属的各灰类，但存在不清晰的边界划分[8-9]，1993年刘思峰[10]首先提出了端点三角白化权函数，2011年他又对传统白化权函数进一步改进，提出中心点三角白化权函数[11].以上学者对白化权函数进行了研究和改进，并建立了相应的灰色聚类评价方法，但是对于划分为同一灰类的聚类对象没有排序，因此只能将聚类对象划分为相应的灰类，不能对聚类对象进行排名.

本文首先改进传统灰色聚类分析中的白化权函数，并对聚类后划分为同一灰类的聚类对象进行排序，进而构建一个聚类后排序的灰色聚类评价方法.结合高校图书馆员的评价实例来说明灰色聚类和排序过程，为图书馆员的选拔、聘任和评价排序提供量化依据.

1 灰色聚类评价方法的设计

设待考核的对象有m个，评估指标有n个，评估结果有s个，即有s个灰类.对象i关于评估指标j的取值为xij，其中i∈[1,m],j∈[1,n]，对象i划分为第k类，其中k∈[1,s].采用灰色聚类方法对xij的取值进行分析、处理，得到考核人员i的评估结果，即评价考核对象i所属的灰色聚类k.

聚类后排序的灰色聚类评价方法设计步骤如下：

（I）确定灰类数及取值范围

按照建立评估模型的要求，划分灰类数s个.同时将评估指标的取值范围按照实际需求划分为s个区间，它们分别为

[a1,a2],…,[aj,aj+1],…,[as-1,as],[as,as+1]

其中aj的值可以根据现实测量或实际数据的取值获得.

（II）确定灰类的转折点和中心点

按照步骤（I）中的灰类数，逐步确定灰类1的转折点，灰类s的转折点和灰类k的中心点，并分别记为λ1j,λsj,λkj，其中k∈[2,s-1].

（III）构建白化权函数

灰类1采用改进的下限测度白化权函数f1(x),灰类s则采用改进的上限测度白化权函数

jijfs(x).改进的下限测度白化权函数在原来下限测

jij度白化权函数的基础上，有效地将聚类指标的取值范围向左延伸.改进的上限测度白化权函数在原来上限测度白化权函数的基础上，有效地将聚类指标的取值范围向右延伸.灰类1和灰类s的白化权函数定义如下：

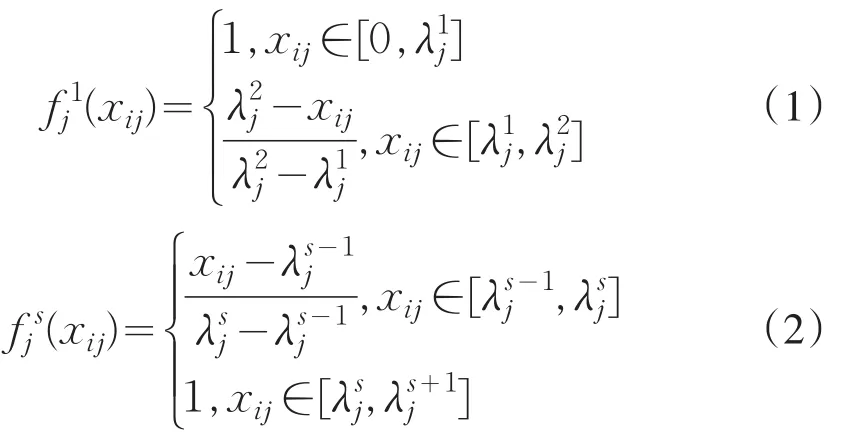
灰类k白化权函数生成过程：中心点为(λkj,1)和(λkj+1,1)，前点为灰类k-2的转折点(λkj-1,0)，后点为灰类k+1的转折点（λkj+2，0），连接前点和中心点、中心点和中心点、中心点和后点，得到灰类k的白化权函数：

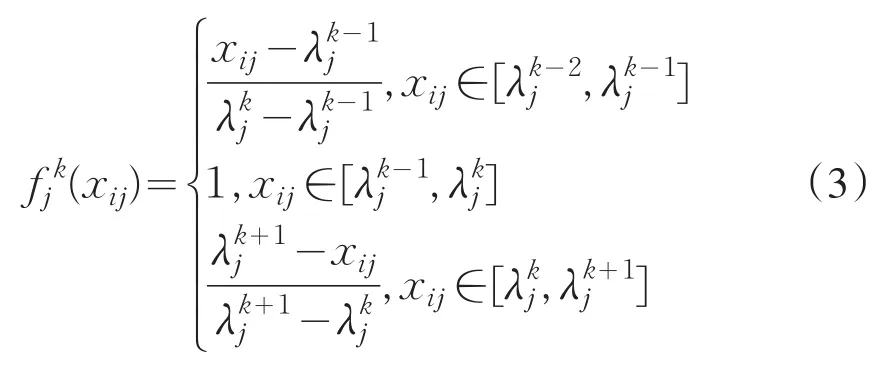
评价方法中构造的白化权函数示意图如图1所示.

图1 构造的白化权函数示意图

（IV）确定灰色聚类指标权重

灰色聚类的权重是对同一灰类划分的权值的衡量指标，一般采用ωj来表示第 j个指标的权重.指标权重分为主观权重和客观权重，主观权重可采用层次分析法计算[12]；客观权重可采用离差最大化法计算[13]；也可以计算主观、客观组合权重系数[14]，通过组合赋权法有效的融合主、客观权重，进而得到灰色聚类的指标权重；当然也可以根据实际数值得到指标权重的值.

（V）计算灰色聚类系数

计算考核对象i对隶属于灰类k的聚类系数σki通过如下公式计算：

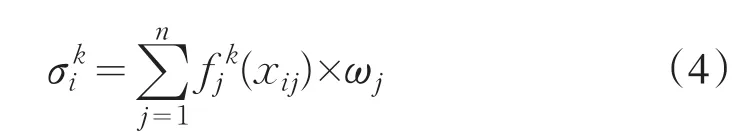
公式（4）中 fjk(xij)是公式（3）中考核对象的 j指标k子类对应的白化权函数，ωj为j指标在考核对象指标中的权重.

（VI）确定灰色聚类

（VII）同一灰类的聚类对象排序

现实中，聚类为同一灰类k中的聚类对象数目多于实际的指标数额，例如“优秀”指标只有1个，而划分为“优秀”灰类的聚类对象有2个或更多.因此需要对不同的聚类对象在该灰类中进行排序，灰色聚类评价方法的排序系数记为δki,若k≠1且k≠s,δki的计算公式为：

由公式（5）和公式（6）计算出同一灰类每个聚类对象的排序系数的大小，按照排序系数δki的大小对属于同一灰类的每个聚类对象进行排序.

2 图书馆员工作评价实例

（I）建立灰色聚类评价矩阵

采用文献[15]中的数据，其中评价对象数为6个，评价指标为5个，量化分值记为xij，其中i为考核对象的编号，i∈[1,6]；j为考核指标的编号，j∈[1,5]，i、j均为整数.将考核对象的评价分为优秀、合格和不合格三种灰类.6名评价对象的评价指标具体评分值见文献[15]表1.由文献[15]表1可得到灰色聚类评价矩阵Ma如下：

（II）灰色聚类评价方法的应用

①确定灰类数及取值范围：灰类数记为s，结合文献[15]中数据，将评价对象的评价分为优秀、合格和不合格三种，所以s=3.其中不合格的取值范围为[40,70]，划分为灰类1；合格的取值范围为[60,86），划分为灰类2；优秀的取值范围为[73,95]，划分为灰类3.

②确定灰类的转折点和中心点：转折点和中心点取平均值，即

③构建灰类的白化权函数：由公式（1）、（2）、（3）得到考核对象的白化权函数：

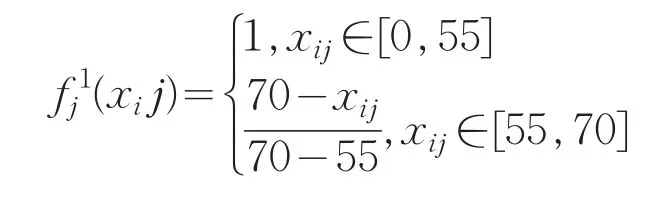
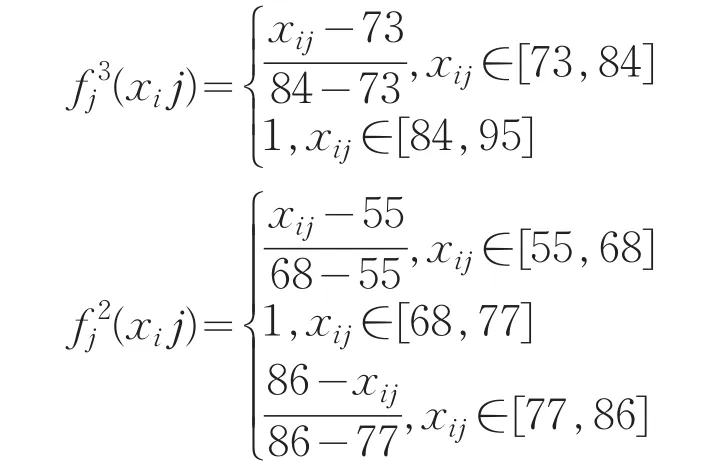
④计算权重：高校图书馆员聚类指标在考核评价中所占权重如表1所示.

表1 图书馆员评价各项指标所占比重

⑤计算灰色聚类系数：聚类系数σki可以很好的反映考核对象i对属于灰类k的聚类程度.聚类系数σki可由公式计算:

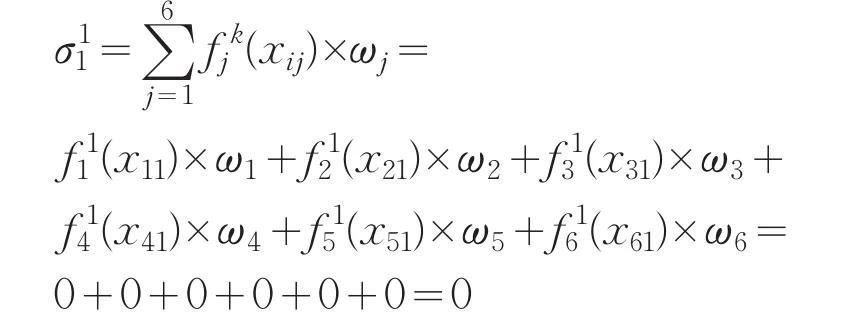
同理可以得到其它考核对象的灰色聚类系数，结果见表2.

表2 考核对象评估聚类系数表

⑥确定灰色聚类：由表2可得到每个考核对象的评价的灰色聚类向量，5个考核对象的灰色聚类向量为

表3 文献[15]和本文方法的聚类结果对比

因为设置灰类的阈值不同，所以最后的聚类结果不同.在现实中，图书馆员工作如果没有重大事故发生，一般评定为“合格”，如果有严重的事故发生，才会评定为“不合格”.因此本文的灰色聚类方法评价结果更与实际情况相符，由于划分为“优秀”灰类的聚类对象可能多于评定为“优秀”的名额指标，因此需要对评价为同一灰类的聚类对象进行排序，尤其是对“优秀”灰类和“不合格”灰类的对象进行排序，按照排序结果进行整体评价.

⑦同一灰类的聚类对象排序：表2可得到划分为该灰类的聚类对象，“优秀”灰类的为考核对象1、考核对象2；“合格”灰类的为考核对象3、考核对象4、考核对象5、考核对象6.由于“优秀”灰类具有2个考核对象，“合格”灰类具有4个考核对象，采用公式6对划分为“优秀”的两个对象进行排序，计算过程为：

虽然灰色聚类中考核对象1、考核对象2都属于“优秀”灰类，但是由于δ31＞δ32，因此考核对象1的排名高于考核对象2.同理可以由公式5求得“良好”灰类中4个聚类对象的排序，“合格”灰类四个考核对象的排序分别为考核对象4、考核对象5、考核对象6、考核对象3.由步骤（VI）和步骤（VII）可得到6个考核对象的最终排名如表4.

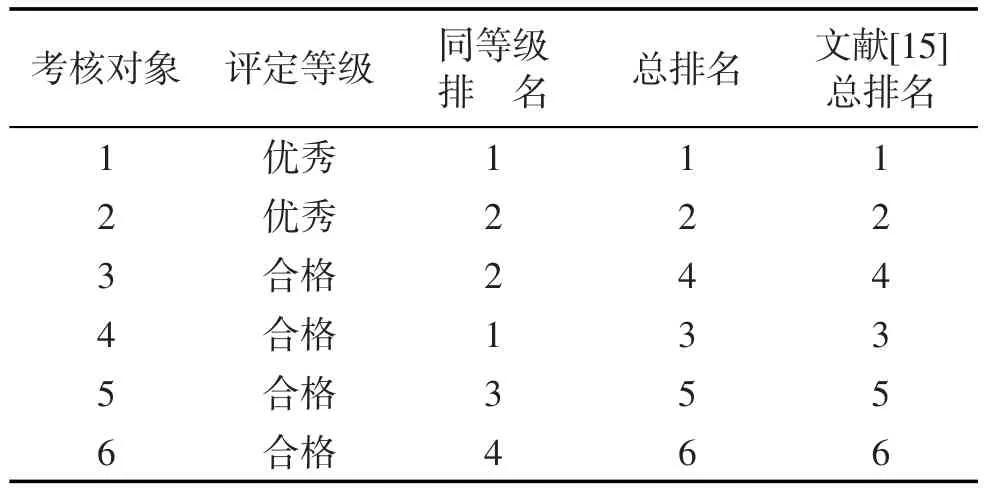
表4 图书馆员评定等级与排名

由表4可以得到6个考核对象最终的排名，本文改进方法和文献[15]采用的评价方法得到的排名顺序一致，但是文献[15]中没有对聚类对象进行排序.本文首先通过对考核对象进行灰类划分，然后对同一灰类的考核对象进行排序，最终得到了全部考核对象的排名.采用聚类后排序的方法，对传统灰色聚类分析法进行改进，为考核对象的排名提供了量化支持，减少了评价过程中的主观性.

3 结语

由于聚类分析具有很强的实用性，所以聚类分析受到了人们的重视并推广应用，其中灰色聚类分析是聚类分析中的新方法，近年来已经逐步发展和完善，通过完善的理论不断应用到很多聚类的领域.灰色聚类分析中的白化权函数对于聚类结果的准确性和实用性具有重要的影响.本文构建了一种改进的聚类后排序的灰色聚类评价方法，首先对白化权函数进行改进，然后通过改进的白化权函数进行灰色聚类，最后对同一灰类的聚类对象进行排序，很好的解决了聚类对象在评价结果中的排序问题，生成一种新的聚类后排序的灰色聚类评价方法.将改进的灰色聚类评价方法应用到图书馆员的工作评价上，验证了排序的灰色聚类方法的实用性，为图书馆员的选拔、聘任和评价提供量化的依据.

[1]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002:1-46.

[2]SMELTZERE,SHAMBAUGHA,STANGELP.Environmentalchangeinlakechamplainrevealedbylongutermmonitoring[J]. JournalofGreatLakesResearch,2012,38(Supplement1):6-18.

[3]赵丹,易英欣.基于灰色聚类评价模型的研究生招生质量研究[J].黑龙江高教研究,2014(11):46-49.

[4]张丽,李广杰,周志广,等.基于灰色聚类的区域地质灾害危险性区域评价[J].自然灾害学报,2009,18(1):164-168.

[5]李星.模糊聚类与灰色聚类在我国证券投资中的应用[D].株洲：湖南工业大学,2012:35-47.

[6]孙晓利,董春,李青元.灰色聚类法在区域经济发展水平综合评价中的应用[J].测绘科学,2008,33(6):160-162.

[7]于俊乐,许青.高校教学管理质量评价信息综合处理方法研究[J].天津师范大学学报,2007,27(2):73-75.

[8]刘思峰,谢乃明.灰色系统理论及其应用[M].第6版.北京:科学出版社,2013:87-95.

[9]LIUSF,XUBIN,JEFFREYFORREST,etal.Onuniformeffect measurefunctionsandaweightedmulti-attributegreytargetdeci⁃ sionmodel[J].JofGreySystem,2013,25(1):1-12.

[10]刘思峰,朱永达.区域评估指标与三角隶属度评估模型[J].农业工程学报,1993,9(2):8-13.

[11]刘思峰,谢乃明.基于改进三角函数白化权函数的灰评估新方法[J].系统工程学报,2011,26(2):244-249.

[12]马农乐,赵中极.基于层次分析法及其改进对确定权重系数的分析[J].水利科技与经济,2006,12(11):732-733.

[13]董一哲,党耀国.基于离差最大化法的灰色聚类方法[J].系统工程理论与实践,2009,29(9):141-146.

[14]陈伟,夏建华.综合主、客观权重信息的最优组合赋权方法[J].数学的实践与认识,2007,37(1):17-21.

[15]王小英,肖新平.基于三角白化函数的灰色聚类决策在图书馆员评价中的应用[C].西安:中国第八届不确定系统年会论文集, 2010:146-152.

【编校：许洁】

AGrayClusteringEvaluationMethodBasedonClusteringandSorting

LIZhiliang,LUOFang,RUANQunsheng
(DepartmentofComputerScience,NingdeNormalUniversity,Ningde,Fujian352100,China)

Onthebasisofthegrayclusteringanalysismethod,thetraditionalwhitenizationweightfunctionwasimproved, andtheevaluationobjectsweresorted,thenthegrayclusteringevaluationmethodwasconstructed.Thenewevaluation methodcannotonlycarryontheclusteringtotheevaluationobjects,butalsosorttheevaluationobjectsofthesamegray class,andsolvetheproblemofclusteringandsortingofclusteringobjects.Byreferencinglibrarians’actualdataanalysis, thegrayclusteringevaluationmethodcaneffectivelyavoidtheblindnessofthelibrarystaffworkevaluation,andprovide quantitativebasisfortheselection,appointmentandevaluationoflibrarystaff.

graycluster;sort;greyclass;jobevaluation

N941.5

A

1671-5365(2015)12-0056-05

李志亮，罗芳，阮群生.一种聚类后排序的灰色聚类评价方法[J].宜宾学院学报,2015,15(12):56-60. LIZL,LUOF,RUANQS.AGrayClusteringEvaluationMethodBasedonClusteringandSorting[J].JournalofYibinUniversi⁃ty,2015,15(12):56-60.

2015-09-27修回：2015-10-11

福建省自然基金项目（2011J01357）；宁德师范学院服务海西项目（2012H405）；福建省大学生创新创业训练计划项目（201410398059）

李志亮（1981-），男，讲师，硕士，研究方向为不确定系统理论

时间：2015-10-1311:33

http://www.cnki.net/kcms/detail/51.1630.z.20151013.1133.002.html