C*代数的离散交叉积

陈本菊，向玉玲，严 倩

（重庆师范大学数学科学学院，重庆401331）

C*代数的离散交叉积

陈本菊，向玉玲，严 倩

（重庆师范大学数学科学学院，重庆401331）

离散群G与C*代数A的交叉积A×αG构成一个新的C*代数，两个离散群G与H构造的半直积G×H仍然构成一个群.交叉积(A×αG)×H与交叉积A×α(G×H)是同构的，因此在一定的条件下C*代数与离散群的交叉积满足结合律.

离散群；C*代数；交叉积；结合律

C*代数主要是应用在量子力学中可观察量的模型代数中.这方面的研究始于维尔纳·海森堡创立的矩阵力学.二十世纪三四十年代Murray和VonNeumann开始算子代数的基础性研究，建立了冯诺依曼代数的系统理论，他们关于中心单代数研究的主要结果之一就是引入交叉积的概念.随后Nakamura开始着重分析研究算子代数的交叉积，特别是描述和构造II1型因子的交叉积.二十世纪五十年代中期，Turumaru明确地给出了C*代数交叉积的概念[1].之后，Nakamura和Takeda紧接着对II1型因子的交叉积进行了一系列的研究[2-3].同时Suzuki研究了算子环的交叉积[4].数学物理学家Doplicher，Kas⁃tler和Robinson为描述一个物理系中的对称性和时间演变过程，引入了共变代数的概念，从而开启了对C*代数在连续群作用下所生成的交叉积的研究[5].交叉积理论不仅可用于算子代数，也可用于非交换几何和物理学.

G×H在如下定义的乘法运算下形成一个群:

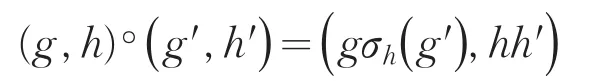
其中g,g′∈G,h,h′∈H.称(G×H,∘)为群G和H在作用σ下的半直积，并记为G×H.在不引起混淆的情况下，简记(g,h)∘(g ′,h′)为(g,h)(g ′,h′).在半直积G×H中单位元是(e,e),(g,h)的逆为:

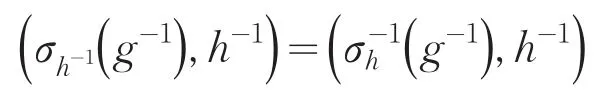
设G是一个可数离散群，则G上的所有平方可和复值函数

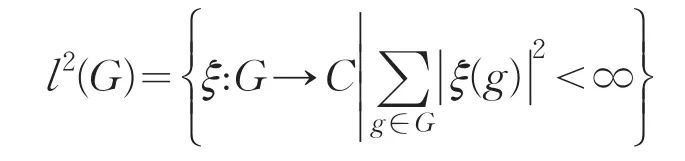
1 准备知识

希尔伯特空间.对于任意h∈G,ξ∈l2(G)，等式(λhξ)(g)=ξ(h-1g )定义了作用在l2(G)上的酉算子λh.此时，h→λh是群G的酉表示，称为群G的左正则表示.称所有算子λg,g∈G生成的C*代数为群

设G和H是有单位元e的可数离散群，σ是从H到G的自同构群Aut(G)内的同态映射.集合G的群C*代数.

设A是作用在Hilbert空间H上的C*代数，α是群G在A上的作用.记定义在G上取值在H中的所有平方可和函数的集合

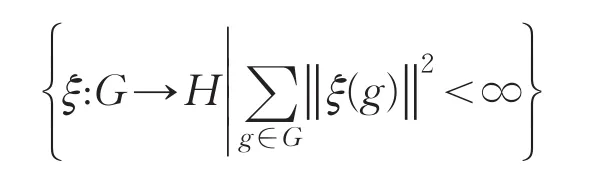
为l2(G,H)，那么l2(G,H)在如下定义的内积:

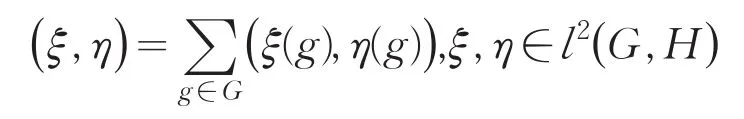
下也形成一个希尔伯特空间.

定义1对于任意的A∈A，定义l2(G,H)上的算子π(A)如下:

(π(A)ξ)(g)=αg-1(A)ξ(g),g∈G,ξ∈l2(G ,H) π是A在希尔伯特空间l2(G,H)上的一个忠实的正规*-表示[6].

引理1l2(G,H)等距同构于H⊗l2(G)[7].

定义2对任意的g∈G，定义l2(G,H)上的有界线性算子λ(g)为:λ(g)=I⊗λg.

定义3称l2(G,H)上由π(A)和λ(G)生成的C*代数为A通过α的交叉积，记作A×αG.

2 主要结果

抽象交叉积与酉实现的交叉积是同构的，因此只考虑酉实现的交叉积.G×H是有单位元e的可数离散群G和H的半直积，A是作用在希尔伯特空间H上的C*代数，α是群G×H在A上的作用.对任意h∈H，义l2(G)上的线性算子Uh为

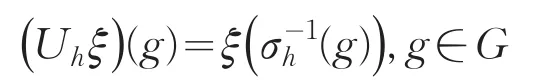
σ是从H到G的自同构群Aut(G)内的同态映射，通过计算可以知道Uh为l2(G)上的酉算子，并且Uh1Uh2=Uh1h2,Uh-1=Uh-1,Ue=I.因此h→Uh是群H 在 l2(G)上的酉表示.类似地，在C*代数A⊗B(l2(G))上 ，对 于 任 意 h∈H ，定 义βh=α(e,h)⊗AdUh，其 中 AdUh(A)=UhAUh*. β∶h→βh是群H在A⊗B(l2(G))上的作用.

记A在希尔伯特空间H⊗l2(G)上的正规忠实表示为π1，C*代数N=A×αG和A在希尔伯特空间H⊗l2(G )⊗l2(H )(= l2(G ×H,H) )上的正规忠实表示分别为π2和π.设ξ∈l2(G,H)，则(U ξ)(g,h)= ξ(σh(g),h),g∈G,h∈H定义了作用在希尔伯特空间l2(G,H)上的有界线性算子U.通过计算有(U*ξ)(g ,h)=ξ(σh-1(g),h).从而有U*U=UU*=I，因此U是一个酉算子.此时π1，π2和π之间有以下关系.

定理1对于任意算子A∈A，有(I⊗U)π(A)(I ⊗U*)=π2(π1(A)).

证明:对任意向量ξ∈H⊗l2(G,H)，(g,h)∈G×H有

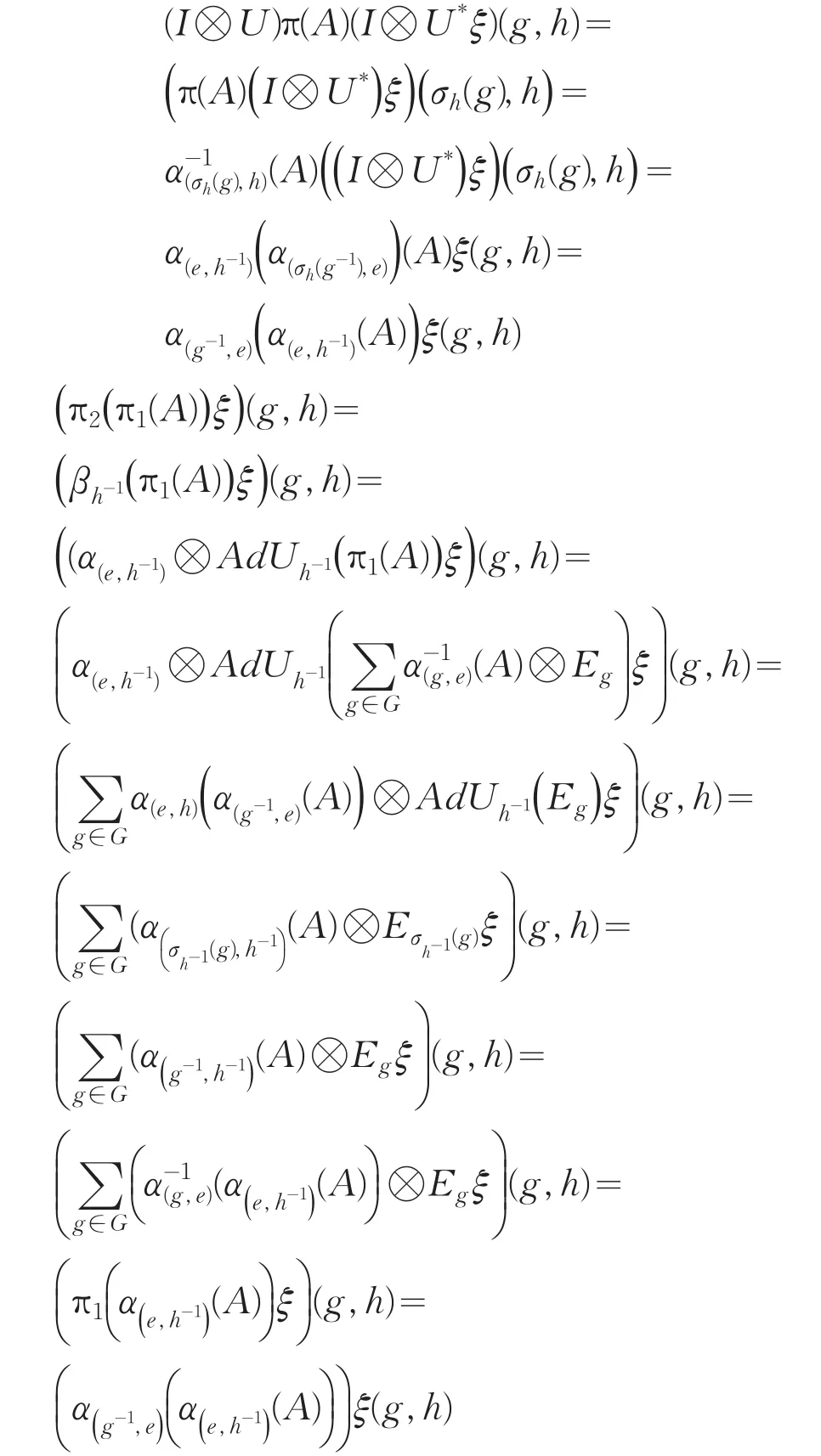
定理2C*代数A在可数离散群G和H的半直积G×H的作用下生成的离散交叉积A×α(G×H)与交叉积(A×αG)×H是*同构的.

证明:由交叉积的定义

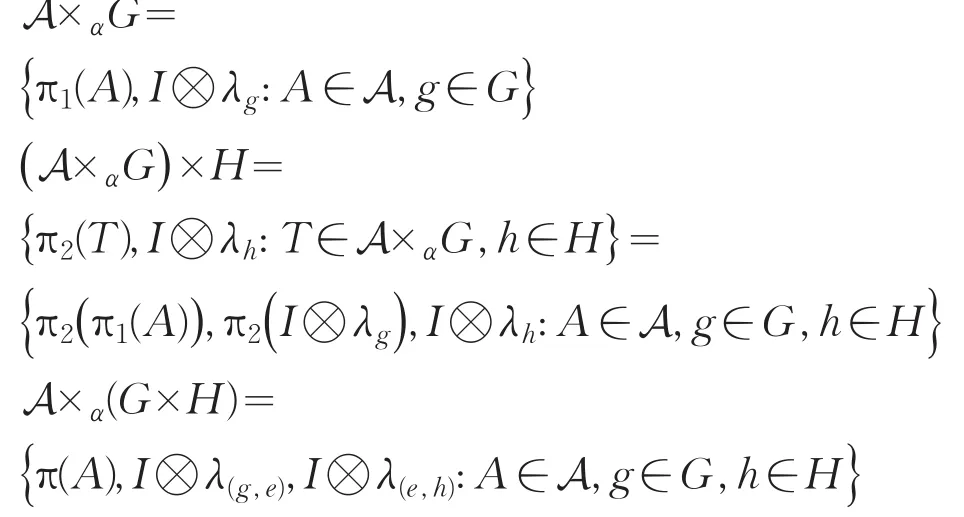
对任意元素 g0∈G,h0∈H,ξ∈l2(G×H),(g,h)∈G×H，有

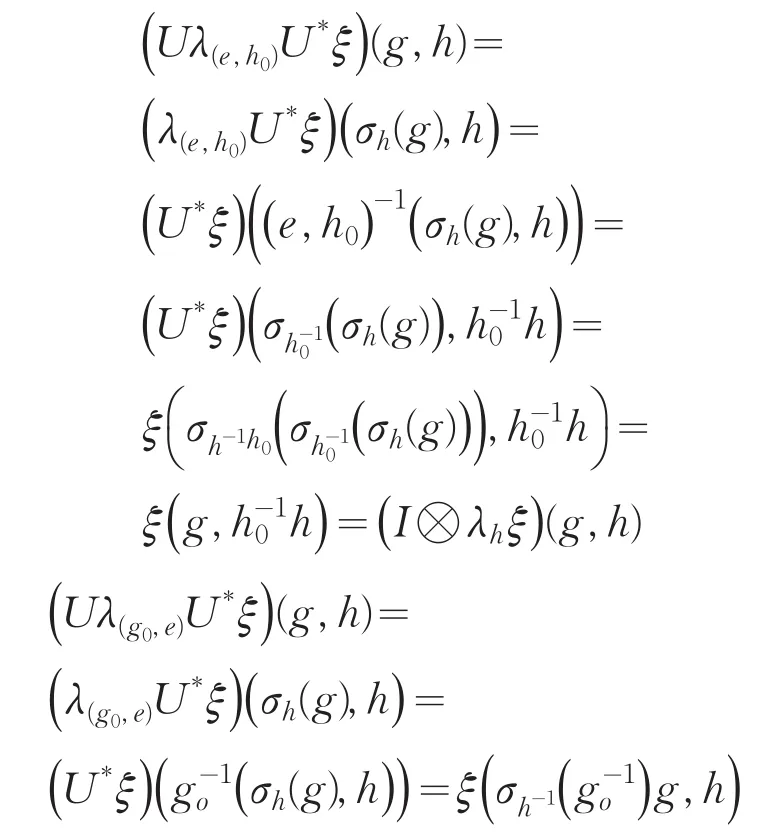
对任意c有

由定理1有

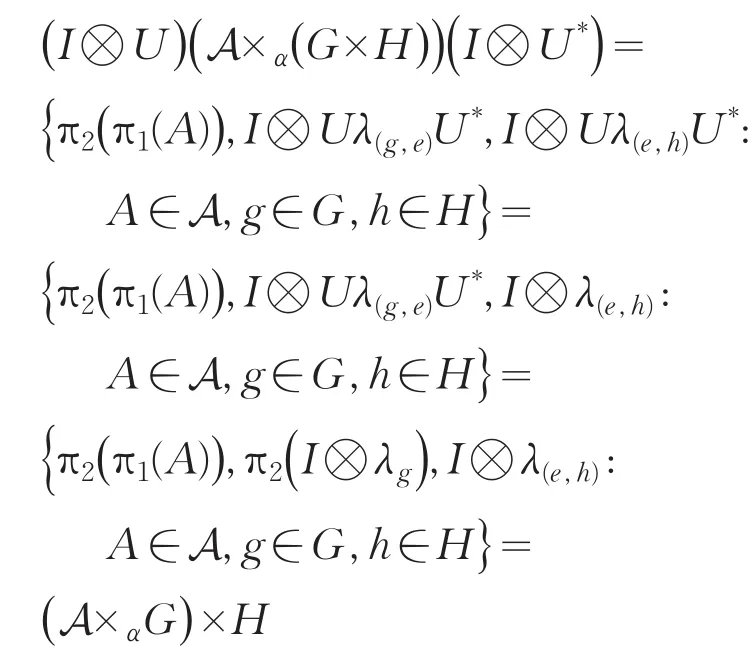
即A×α(G×H)与(A×αG)×H是酉等价的，也是*同构的.

例1：设群G=Z2，群H=Z3，A是作用在Hilbert空间H上的C*代数.则有 A×α(G×H)≅(A×αG)×H.

证明:A在H⊗l2(G)上的正规忠实表示为π1，N=A×αG和A在Hilbert空间H⊗l2(G)⊗l2(H)上的正规忠实表示分别为π2和π.则由题设可知：

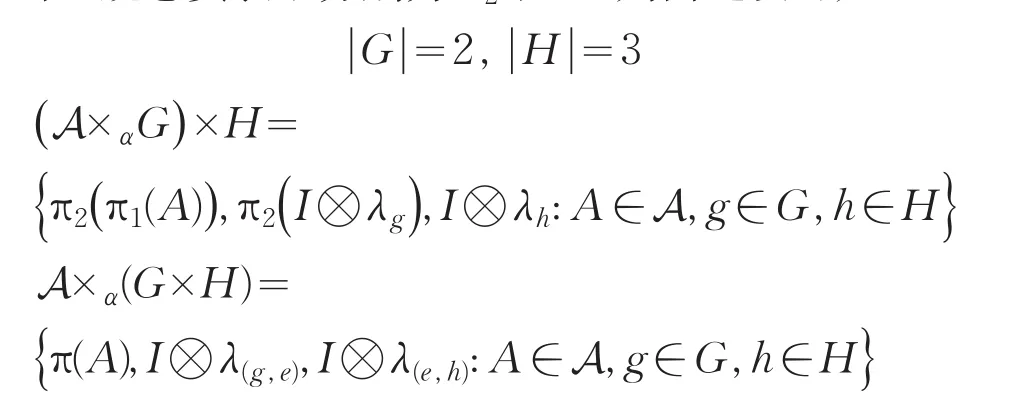
所以有：

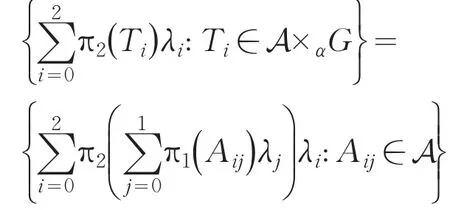
在(A×αG)×H中稠密;

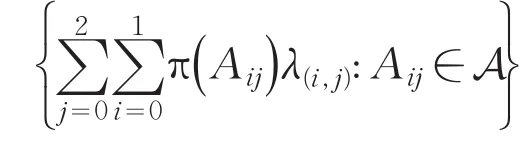
在A×α(G×H)中稠密.

因此，A×α(G×H)与(A×αG)×H是*同构的.

[1]TURUMARUT.Crossedproductofoperatoralgebras[J].Tohoku Math,1958,10(3):355-365.doi:10.2748/tmj/1178244669.

[2]NAKAMURAM,TAKEDAZ.Onsomeelementarypropertiesof thecrossedproductsofvonNeumannalgebras[J].ProcJapanAcad, 1958,34(8):489-494.doi:10.3792/pja/1195524559.

[3]NAKAMURAM,TAKEDAZ.AGaloistheoryforfinitefactors[J]. ProcJapanAcad,1960,36(5):258-260.doi:10.3792/pja/ 1195524026.

[4]SUZUKIN.Crossedproductofringsofoperator[J].TohokaMath, 1959,11(1):113-124.doi:10.2748/tmj/1178244632.

[5]DOPLICHERS,KASTLERD,ROBINSOND.Covarianealgebras infieldtheoryandstatisticalmechanics[J].CommMathPhys,1966, 3(1):1-28.

[6]杨芳.关于离散群的半直积与VonNeumann代数的交叉积[J].宜宾学院学报,2006(12):13-14.

[7]吴文明,袁巍.冯·诺依曼代数交叉积的一点注记[J].数学学报, 2008,51(4):803-808.

【编校：许洁】

DiscreteCrossedProductofC*-Algebras

CHENBenju,XIANGYuling,YANQian
(CollegeofMathematicsSciences,ChongqingNormalUniversity,Chongqing401331,China)

Crossedproduct(A×αG)×HisstructuredbyA×αGandH,andcrossedproductA×α(G×H)isstructured byC*-algebrasAandsemi-directgroupsG×H.Itshowsthat(A×αG)×HandA×α(G×H)isisomorphic,andthey satisfytheassociativelow.

discretegroups;C*-algebra;crossedproduct;associativelaw

O177.5

A

1671-5365(2015)12-0095-03

陈本菊，向玉玲，严倩.C*代数的离散交叉积[J].宜宾学院学报，2015，15(12):95-97.

CHENBJ，XIANGYL，YANQ.DiscreteCrossedProductofC*-Algebras[J].JournalofYibinUniversity,2015,15(12):95-97.

2015-09-10修回：2015-10-19

陈本菊(1987-),女,硕士研究生,研究方向为算子代数

时间：2015-10-1911:20

http://www.cnki.net/kcms/detail/51.1630.z.20151019.1120.001.html