一个含混合核的Hilbert型积分不等式

有名辉

（浙江机电职业技术学院数学教研室，浙江杭州310053）

一个含混合核的Hilbert型积分不等式

有名辉

（浙江机电职业技术学院数学教研室，浙江杭州310053）

通过引入多个参数，建立一个具有最佳常数因子的Hilbert型积分不等式，并给出其等价形式，推广了相关文献的结果．

Hilbert型不等式；等价形式；Euler数；Hölder不等式；Gamma函数

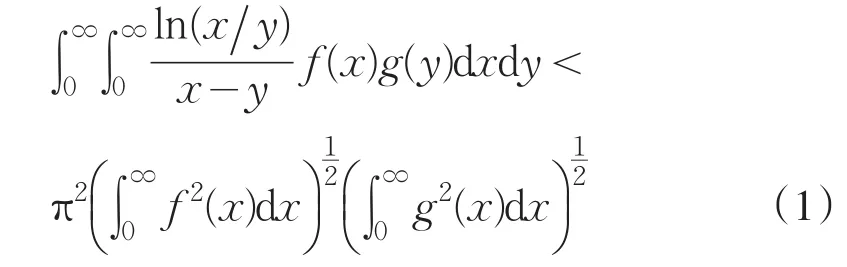
其中π2是满足（1）式的最佳常数因子[1].通常称不等式（1）为Hilbert型不等式.Hilbert型不等式在分析学及其应用领域有着重要的作用[2].近年来，通过引进参数，研究者们给出了（1）式及其对应的级数形式的一些推广和改进，建立了一些深刻且有价值的成果[3-8].

2011年，周昱、高明哲[9]又证明了一个类似于（1）式并与Euler数有关的不等式，即其中λ＞0,E0=1,En(n∈N+)是Euler数，即E1=1, E2=5,E3=61,E4=1385…

本文的目的是建立一个含有混合核的Hilbert型积分不等式，它是（2）式的推广.首先给出以下定义及引理.

定义[10]对于a＞0,定义：

为第二型欧拉积分，即Γ函数.特别地，当a∈ℤ+时，Γ(a)=(a-1)!.

为行文方便，以下约定：

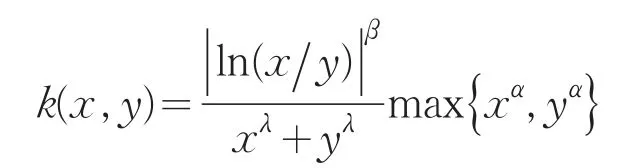
引理 1设 λ＞0,0≤α＜λ,β≥0,2r=λ-α,则：

因此

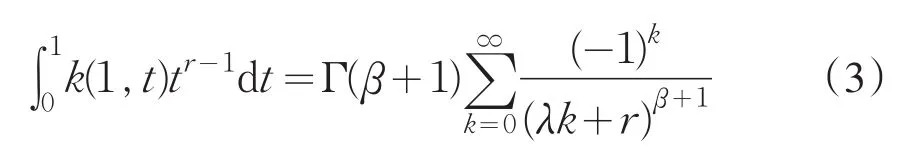
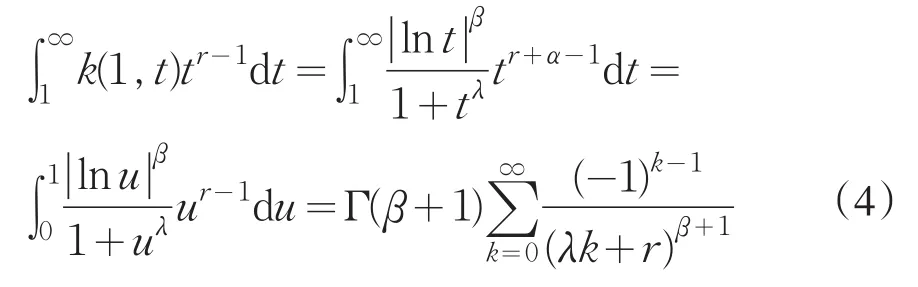
结合（3）式和（4）式，即得引理1.

引理2设β≥0,2r=λ-α,则ε→0+时，有：

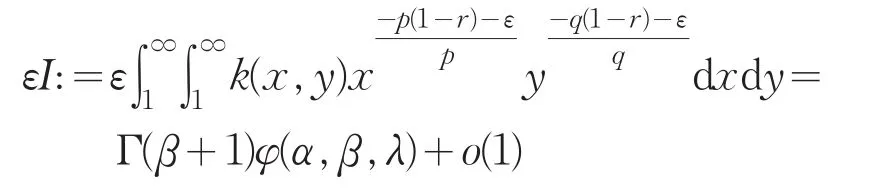
证明：作变量替换y=ux,注意到2r=λ-α,由Fubini定理可知：

当ε→0+时，由引理1，可得

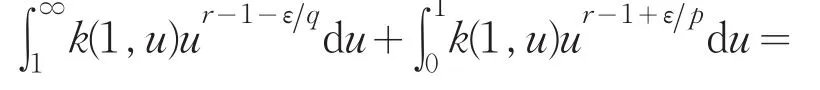
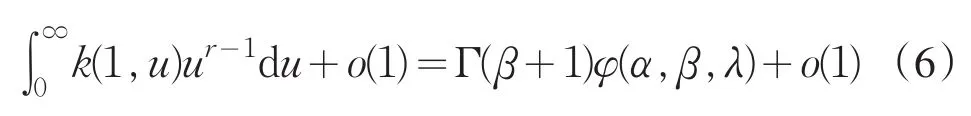
由（5）式和（6）式，即得引理2.

下面是本文的主要结果.

定理1设β≥0,2r=λ-α,f(x),g(x)≥0,满足

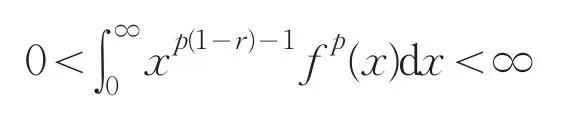
且

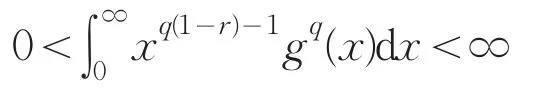
则

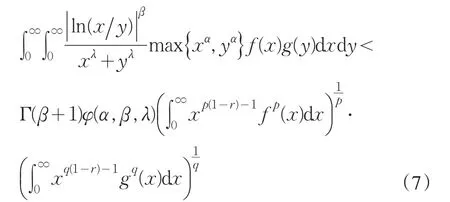
其中φ(α,β,λ)由引理1定义，Γ(β+1)φ(α,β,λ)是满足（7）式的最佳常数因子.

证明：由Hölder不等式，可知：

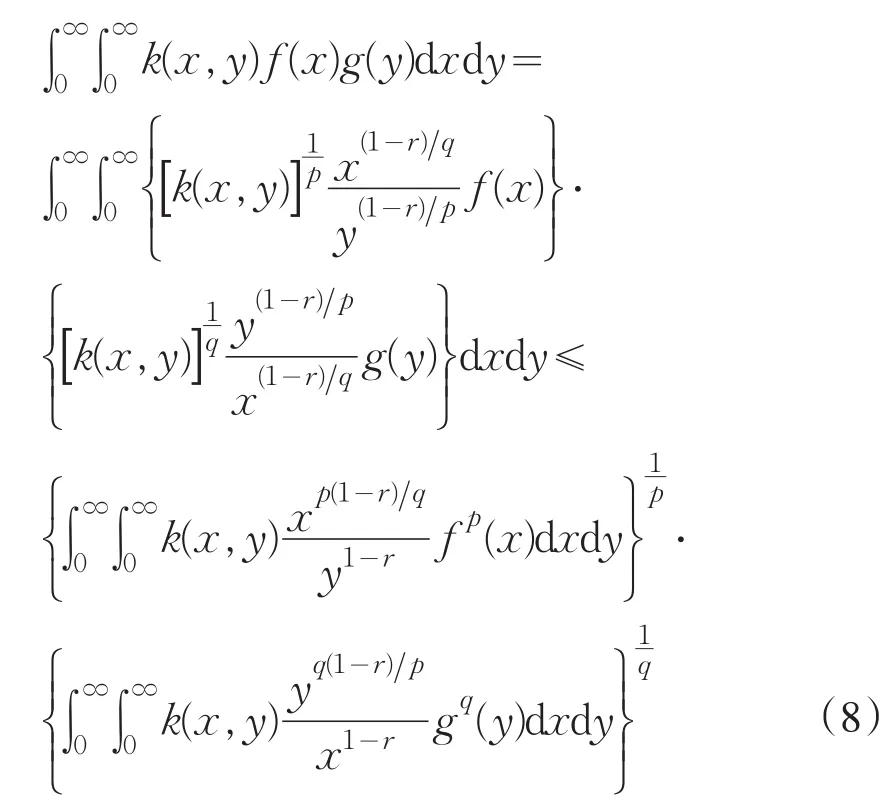
若（8）式取等号，则有不全为零的实数A与B,使得

即：

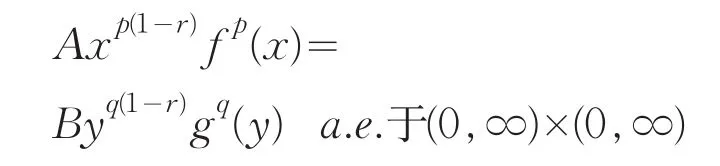
于是，有常数C，使得

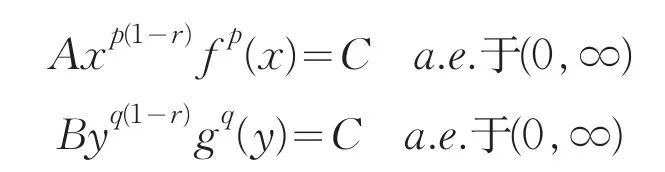
通过变量替换，根据引理1,结合2r=λ-α,不难算得：

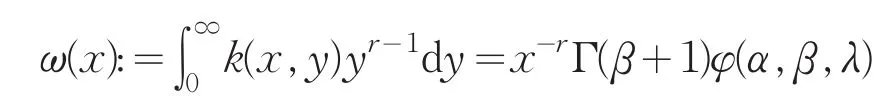
类似地，可算得

“把社区命名为‘腾飞’，就是希望大家跟着飞机一起腾飞，早日过上好日子。”响水乡宣传委员颜登席说，乡里拟投资3.17亿元启动70余个建设项目，把响水乡打造成一个4A级景区。“现在，不仅是腾飞社区依托机场建设‘腾飞’，整个响水乡也和毕节一样，依托立体交通网络在‘腾飞’。”

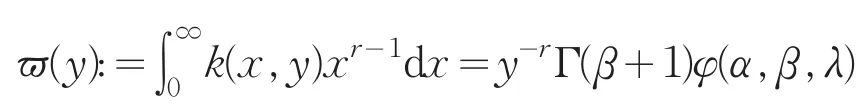
因此（8）式可写成

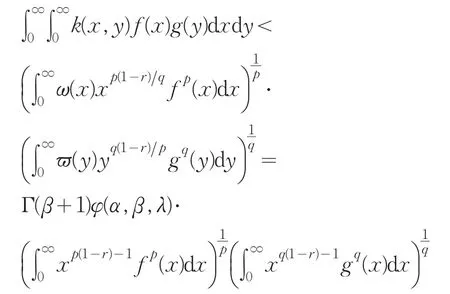
以下将证明（7）式中的常数因子Γ(β+1)φ(α,β,λ)为最佳值.事实上，若此常数因子不为最佳，则存在实数k( ) 0＜k＜Γ(β+1)φ(α,β,λ),使得（7）式中的常数因子换成k后（7）式仍成立.即

定义函数 fε(x)和gε(x)（其中ε充分小）如下：

①若x∈(0,1),令 fε(x)=gε(x)=0;

用 fε和gε分别取代（9）式中的 f和g,则：

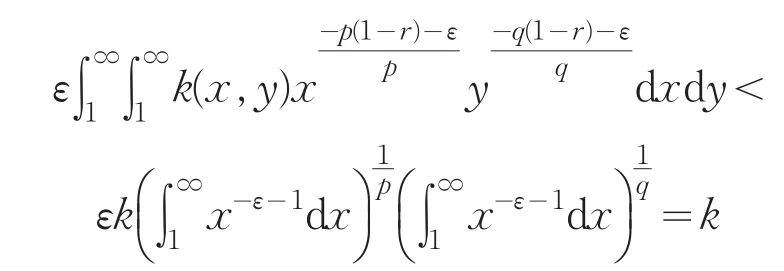
把引理2的结果代入，可得

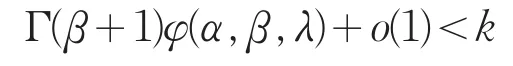
令 ε→0+，则 k≥Γ(β+1)φ(α,β,λ)，这与 k＜ Γ(β+1)φ(α,β,λ)矛盾.故（7）式中的常数因子为最佳值.定理1证毕.

其中[Γ (β+1)φ(α,β,λ)]p是满足（10）式的最佳常数因子，且（10）式和（7）式等价．

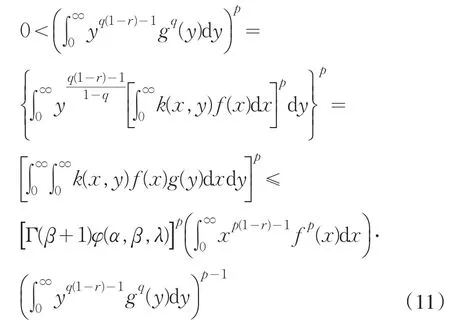
故

结合定理2的条件和（12）式可知应用定理1的条件是充分的.因此（11）式和（12）式都取严格不等号.故（10）式成立.

以上从（7）式证得了（10）式.要说明（7）式和（10）式等价，以下只需从（10）式证得（7）式.事实上，由Hölder不等式，可知

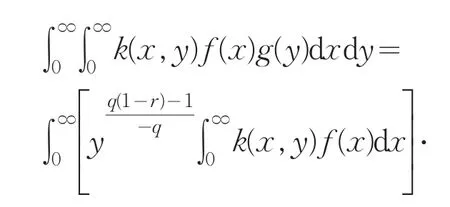
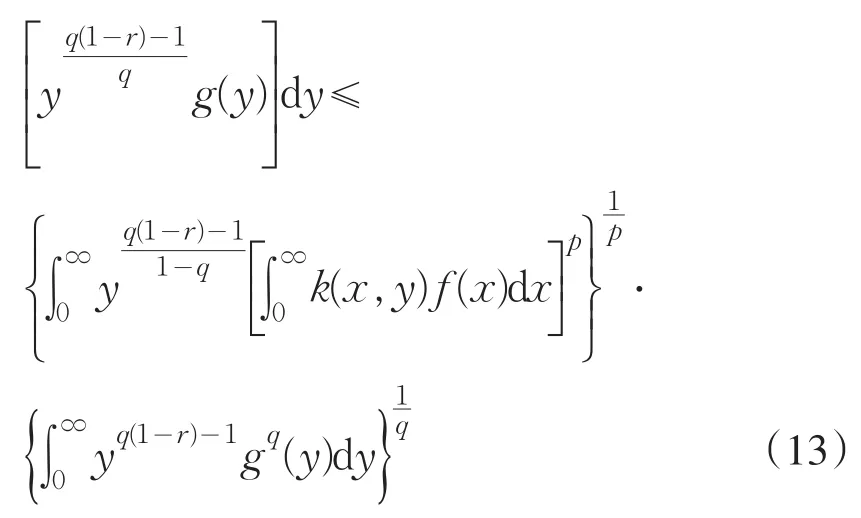
把（10）式代入到（13）式，可知（7）式成立.若（10）式中的常数因子[Γ (β+1)φ(α,β,λ)]p不是最佳值，则由（10）式和（13）式证得的（7）式的常数因子也不是最佳的，这显然矛盾.故（10）式中的常数因子是最佳值.

定理2证毕.

在定理1中,令α=0,β=2n,注意到[12]

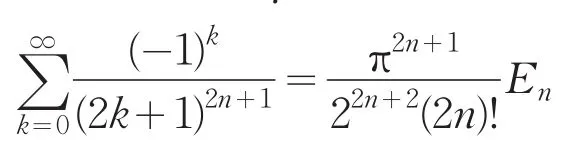
则有下面推论.

推论1设p＞1,n是非负整数，f(x),g(x)≥0，满足∞且则：

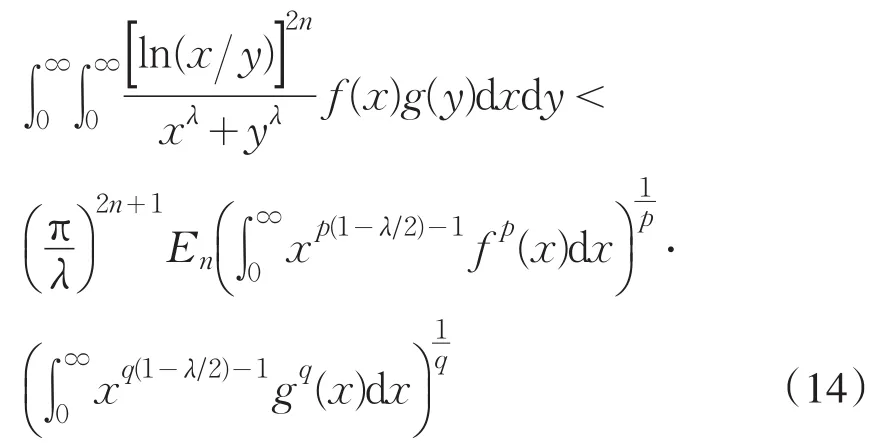
在（14）式中,令p=q=2,即得（2）式,因此定理1是（2）式的推广.

在定理1中,令β=0,则有以下负齐次核Hil⁃bert型不等式：

推论2设p＞1,2r=λ-α,f(x),g(x)≥0,满足

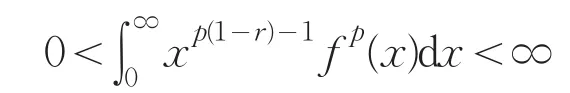
且

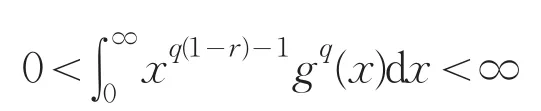
则：

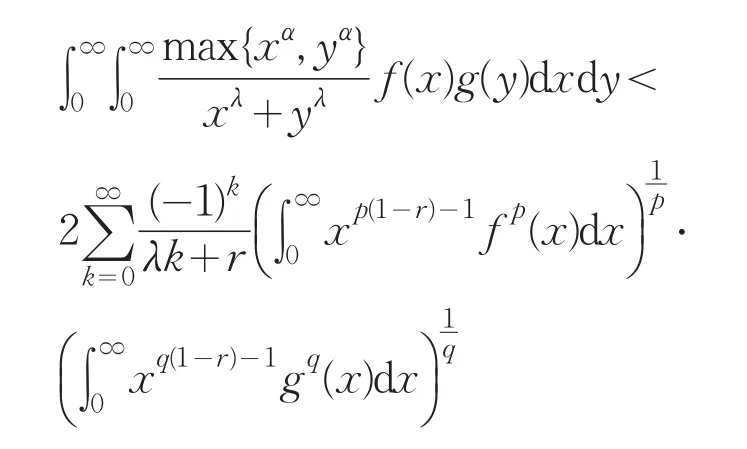
[1]HARDYGH,LITTLEWOODJE,POLYAG.Inequalities[M].Lon⁃don:CambridgeUniversityPress,1952.

[2]MINTRINOVICDS,PECARICJE,FINKAM.Inequalitiesinvolv⁃ingfunctionsandtheirintegralsandderivatives[M].Boston:Kluwer Academic,1991.

[3]杨必成.关于一个Hilbert类积分不等式的推广及应用[J].应用数学,2003,16(2):82-86.

[4]杨必成.关于一个推广的具有最佳常数因子的Hilbert类不等式及其应用[J].数学研究与评论,2005,25(2):341-346.

[5]KUANGJC,DEBNATHL.OnNewgeneralizationsofHilbert’s inequalityandtheirapplications[J].JMathAnalAppl,2000,245 (1):248-265.

[6]JINJJ.AnewgeneralizationofHardy-Hilberttypeinequalitywith multi-parameters[J].JMathResExposition,2009,29(6):1131-1136.

[7]JINJJ.OnHilbert'stypeinequalities[J].JMathAnalAppl,2008, 340(2):932-942.

[8]杨必成.一个较为精密的Hardy-Hilbert型不等式及其应用[J].数学学报(中文版),2006,49(2):363-368.

[9]周昱,高明哲.一个新的带参数的Hilbert型积分不等式[J].数学杂志,2011,31(3):575-581.

[10]菲赫金哥尔茨 ΓΜ.微积分学教程（第二卷）[M].北京:高等教育出版社,2006.

[11]匡继昌.常用不等式[M].济南:山东科学技术出版社,2003.

[12]王连祥,方德植.数学手册[M].北京:人民教育出版社,1979.

【编校：许洁】

ANewHilbert-TypeIntegralInequalityInvolvingMixedKernel

YOUMinghui
（MathematicsTeachingandResearchSection,ZhejiangInstituteofMechanicalandElectricalEngineering,Hangzhou,Zhejiang 310053,China）

Byintroducingmultipleparameters,anewHilbert-typeinequalityanditsequivalentformwereestablished, andsomeknownresultswereextended.

Hilbert-typeinequality;equivalentform;Eulernumber;Hölderinequality;Gammafunction

O178

A

1671-5365(2015)12-0091-04

有名辉.一个含混合核的Hilbert型积分不等式[J].宜宾学院学报,2015,15(12):91-94.

YOUMH.ANewHilbert-TypeIntegralInequalityInvolvingMixedKernel[J].JournalofYibinUniversity,2015,15(12):91-94.

2015-06-24修回：2015-07-09

有名辉（1982-），男，讲师，硕士，研究方向为解析不等式

时间：2015-07-1010:35

http://www.cnki.net/kcms/detail/51.1630.Z.20150710.1035.001.html