涡量流函数法模拟方腔内粘性不可压流动

李江飞，李岩芳，谢冬梅，段兴华，张 康，胡 凯，逯国强，李宏磊

（承德石油高等专科学校热能工程系，河北承德067000）

涡量流函数法模拟方腔内粘性不可压流动

李江飞，李岩芳，谢冬梅，段兴华，张 康，胡 凯，逯国强，李宏磊

（承德石油高等专科学校热能工程系，河北承德067000）

通过对涡量控制方程进行无量纲化推导和离散，用联合迭代方法求解二维方腔流动这一不可压缩黏性典型流动的解析解.基于Matlab编程，采用涡量流函数法求解二维方腔流动，计算采用有限体积算法，对流项采用QUICK格式，扩散项采用二阶中心差分格式，并采用延迟修正技术的离散格式对该问题进行数值求解，得到流动达到稳定状态时各物理量的分布.

数值模拟；方腔流动；涡量流函数；有限容积法

Peng等[1]针对二维不可压缩黏性流体方腔流动边界条件：流动速度u、v采用无滑移边界条件，利用动量方程推导了压力p的边界条件，本文课题组曾采用交错网格MAC算法求解二维方腔流动[2]，本文在此基础上，拟用涡量流函数法模拟方腔内的粘性不可压流动，以得到流动达到稳定状态时各物理量的分布.

1 问题分析

1.1 涡量控制方程无量纲化

守恒型涡量控制方程为：

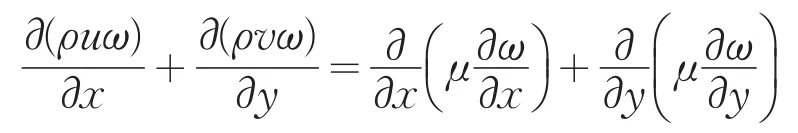
流函数控制方程为：

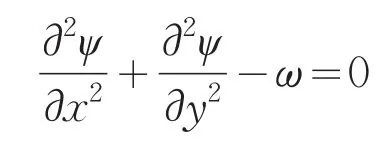
用方腔高度H、流体密度ρ,和拖动速度utop作为无量纲标尺，将控制方程无量纲化.无量纲化后的控制方程：

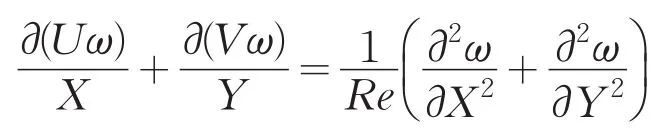
上式中：

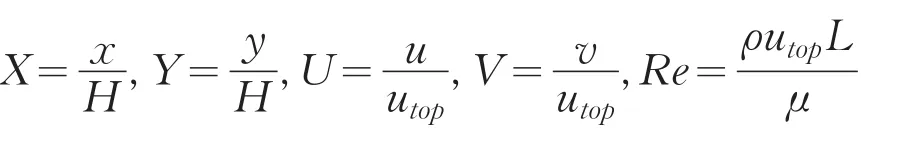
其中：H是方腔长度和高度；utop为顶盖拖动速度；u指变量ϕ在水平x方向的流速；v为变量ϕ在垂直y方向的流速；μ为黏度；ρ为流体密度；ω是涡量；ψ为流函数.

1.2 边界条件

边界条件为：流动速度采用无滑移边界条件，壁面处法向速度恒为0，切向速度也为0.顶盖u=1, v=0;其余u=v=0.

流函数的边界条件为：

涡量的边界条件为：

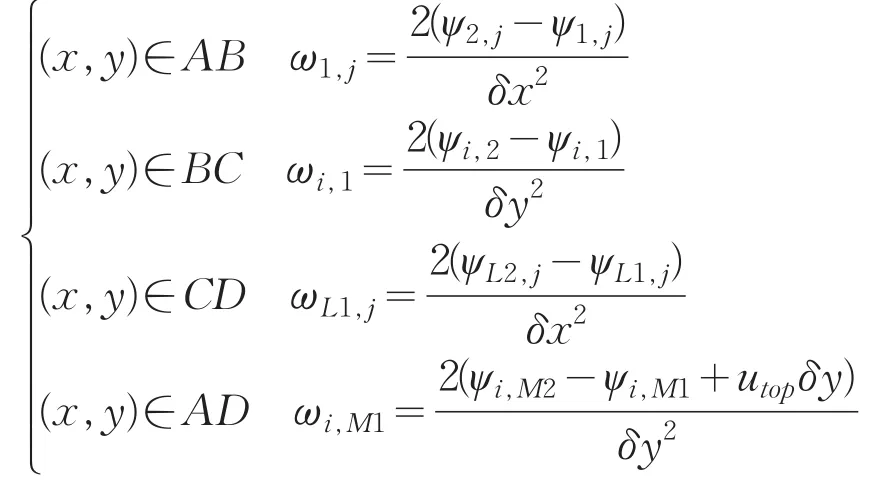
2 方程离散与算法分析

2.1 离散控制方程

涡量控制方程为[3-4]：

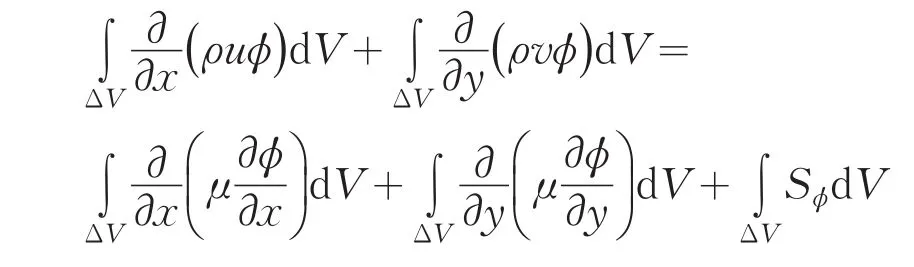
对流项采用QUICK格式[5]：

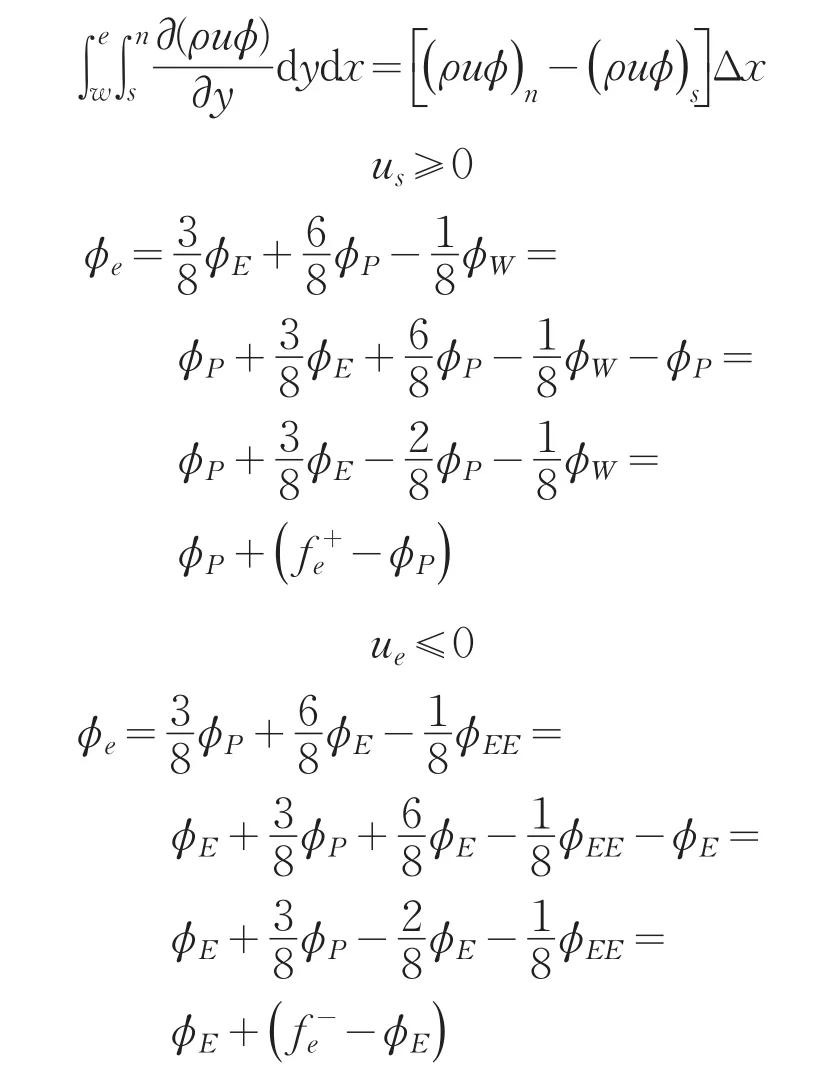
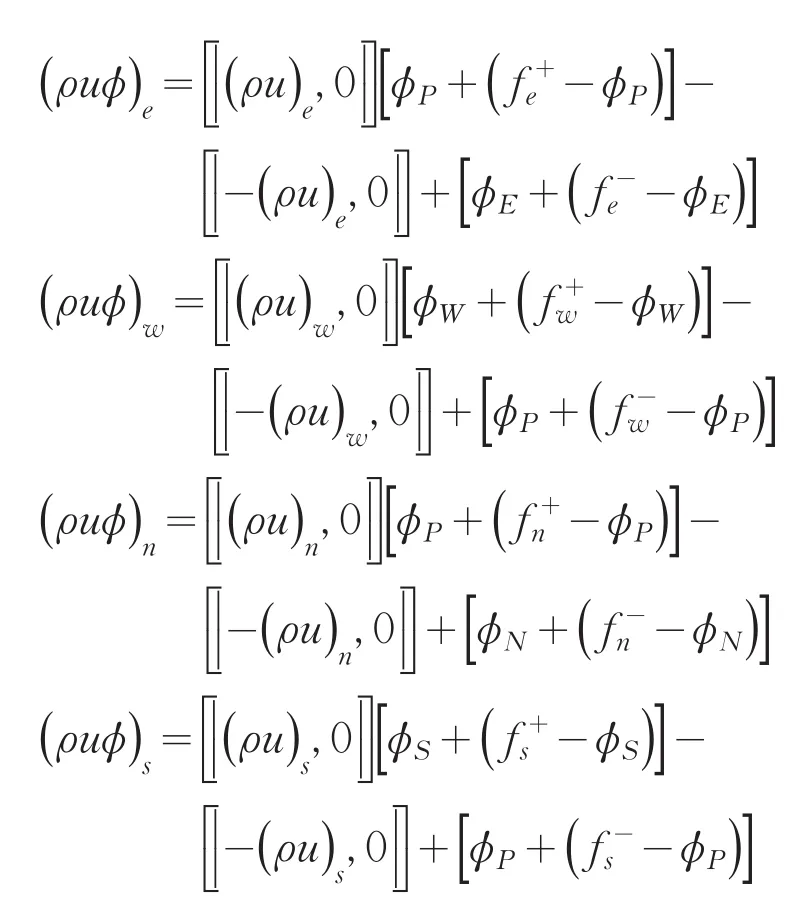
对流项涡量内边界点采用一阶迎风格式：

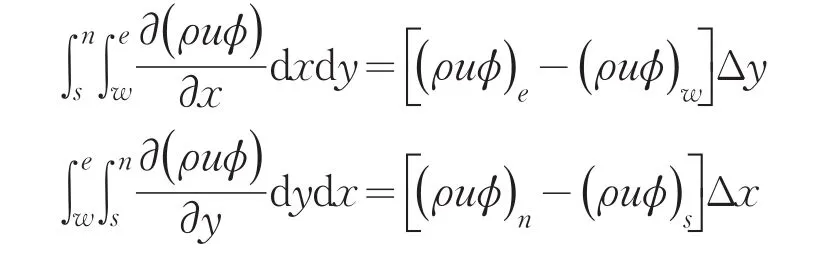
扩散项二阶中心差分格式为[6]：

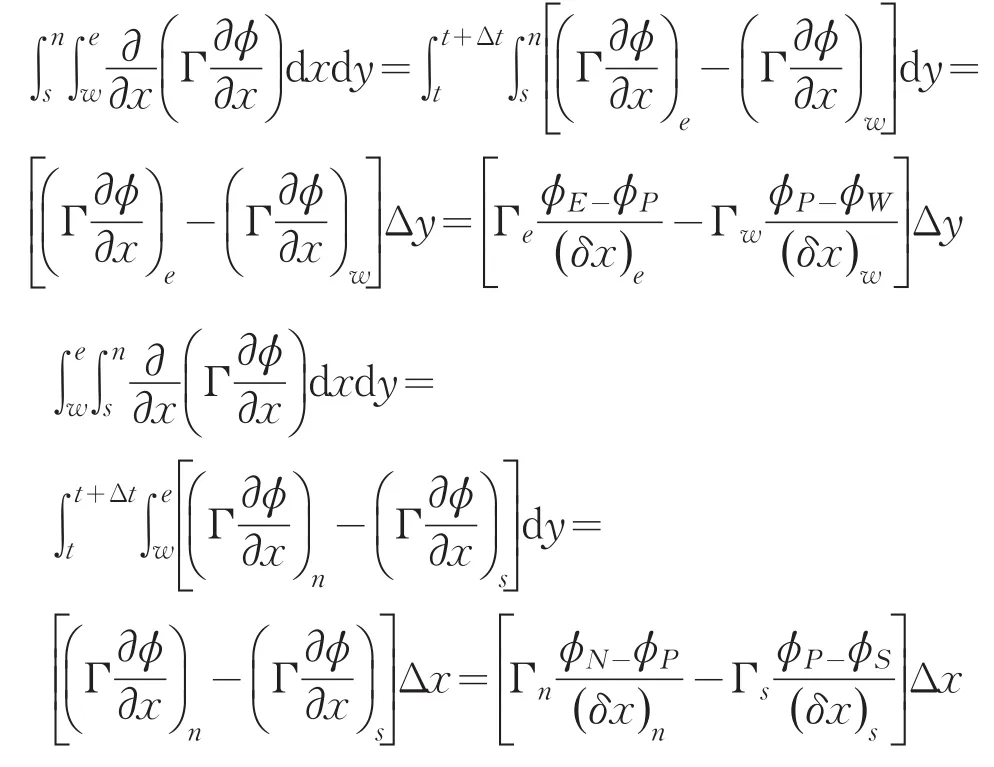
离散代数方程及系数表达式为：

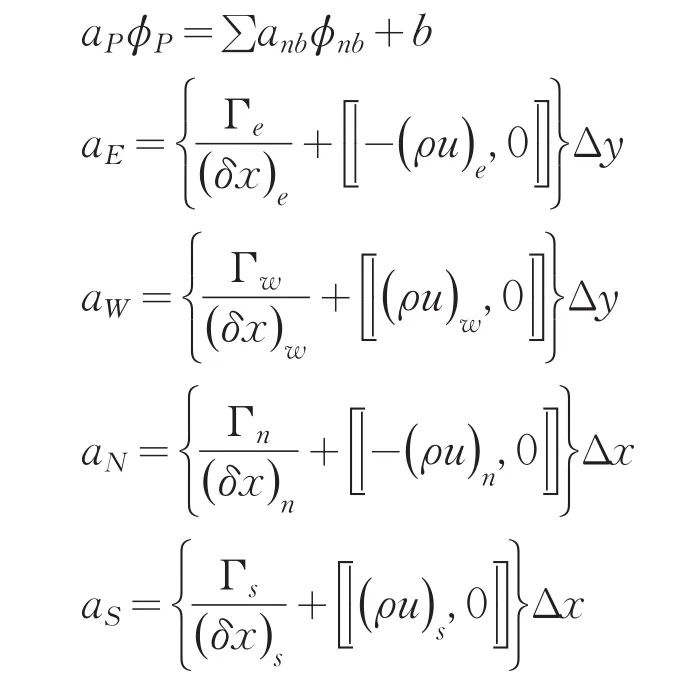
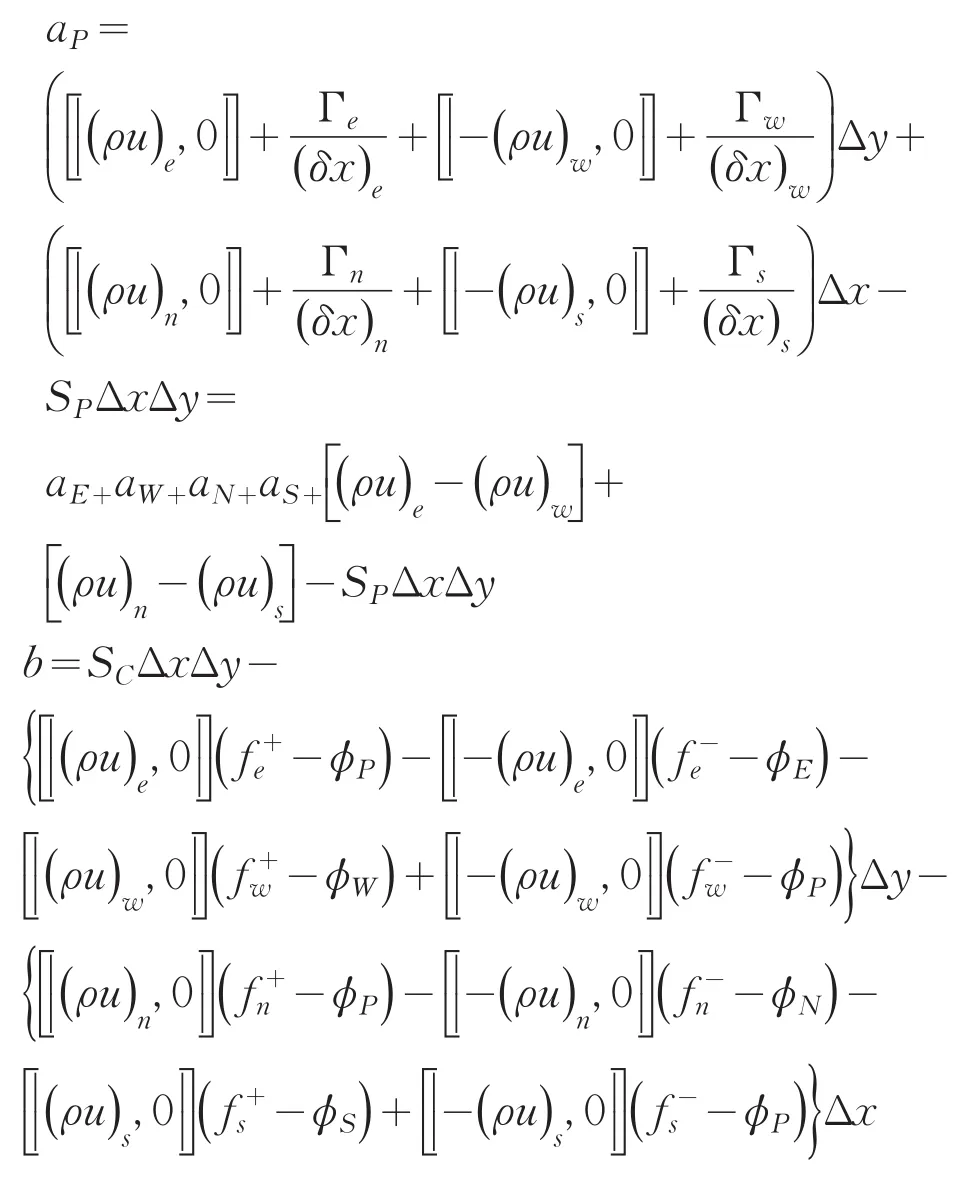
流函数的离散采用中心差分格式：

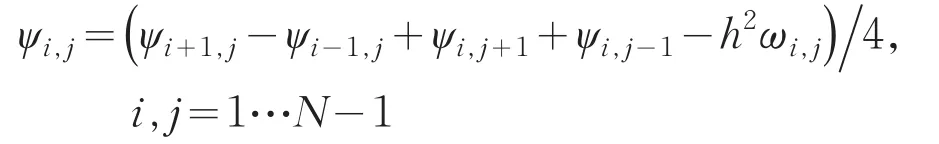
2.2 求解步骤及程序框图

离散方程可采用联合迭代方法求解[7-8]：

（1）根据ψ0i,j计算u、v,确定离散方程的系数；

（2）求解涡量代数方程，得ω0i,j；

（3）由ω0i,j求解流函数方程，得ψ1i,j；

（4）根据ψ1i,j和边界条件确定涡量边界值ω1B；

（5）根据ψ1i,j和ω0i,j,迭代计算直至收敛；

（6）利用压力的Poisson方程计算压力.

具体流程如图1所示.

涡量方程式与流函数方程是互相耦合的，涡量以源项形式出现在流函数方程中，而涡量方程中对流项的系数则由流函数所决定.假设流函数的一个分布，利用该分布计算u和v，从而确定离散方程的系数；接下来计算涡量和流函数.在获得了流函数的收敛解后，可用各节点上的流函数离散处理压力Poisson方程，从而计算压力[3].在获得了流函数的收敛解后，压力方程的源项即可用各节点上的ψ值进行离散处理.

3 结果分析

通过比较不同雷诺数（100和1000）分别在网格数为20、40、80、100时的流线图，可以看出网格数对结果的影响并不是很大，在精度要求不高时可以采用网格数较少的计算，节省时间.稳定状态时，Re=1000，网格数=20×20、40×40、80×80、100×100的涡量图和流函数图，计算结果如图2所示.

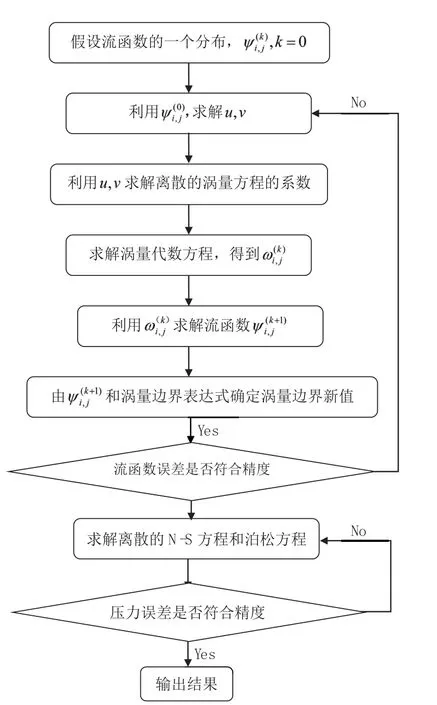
图1 计算程序框图

稳定状态时，Re=10、100、1000的流线图，计算结果如图3所示.

稳定状态时，Re=1000，网格数=20×20，100× 100的压力、u、v及其中心线速度分布图，计算结果如图4所示.

对图2、图3、图4的计算结果进行分析，可知：

（1）二维不可压缩黏性流体方腔流动的中心大涡并不在中心位置，方腔内流动也并不对称，表明是带奇性的方腔流动.

（2）本文处理压力边界条件时，分别采用动量方程和NeumannBoundary两种方法，计算结果比较理想.

（3）随着雷诺数的增大，在方腔的两个底角开始出现二次涡流，说明有限体积算法QUICK格式计算精度较高.

（4）通过分析，对流扩散方程中当对流项占主要作用的时候，很容易得到与网格数无关的解.

（5）本文计算分别采用延迟修正处理和不采用延迟修正处理两种方法.延迟修正处理能保证方程对角占优，减少求解时间.

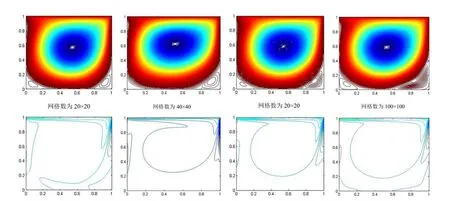
图2 不同网格数下的涡量图和流函数图（Re=1000）

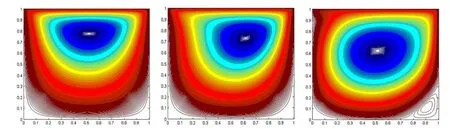
图3 不同雷诺数下的流线图（自左至右：Re=10，100，1000）

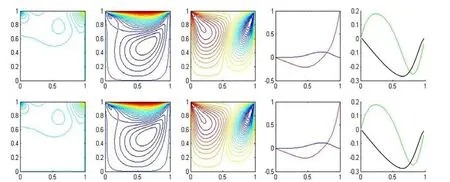
图4 压力、u、v及其中心线速度分布图（Re=1000,网格数=20×20,100×100）

[1]PENGYF,SHIAUYH,HWANGRR.Transitionina2-Dliddrivencavityflow[J].Computer&Fluids,2003,32(3):337-352.

[2]李江飞，石兆东，段兴华，等.MAC算法计算二维方腔顶盖流动[J].宜宾学院学报，2015，15（6）：28-31.

[3]陶文铨.数值传热学[M].第二版.西安:西安交通大学出版社，2001：301-305.

[4]LIUCH,LEUNGDYC.Developmentofafiniteelementsolution fortheunsteadyNavier-Stokesequationsusingprojectionmethod andfractionalθ-scheme[J].Computermethodsinappliedmechan⁃icsandengineering.2001,190(32-33):4301-4317.

[5]AYDINM,FENNERRT.Boundaryelementanalysisofdrivencav⁃ ityflowforlowandmoderateReynoldsnumbers[J].IntJNumer MethFluids,2001,37(1):45-64.

[6]BRUNEAUCH,SAADM.The2Dlid-drivencavityproblemrevis⁃ited[J].Computers&Fluids2006,35(3):326-348.

[7]MERCANH,ATALIKK.Vortexformationinlid-drivenarc-shape cavityflowsathighReynoldsnumbers[J].EuropeanJournalofMe⁃chanicsB/Fluids,2009,28(1):61-71.

[8]WANGJ,LIJF,CHENGWX,etal.ComparisonofFiniteDifference andFiniteVolumeMethodforNumericalSimulationoftheIncom⁃pressibleViscousDrivenCavityFlow[J].AdvancedMaterialsRe⁃search,2013.doi:10.4028/www.scientific.net/AMR.732-733.413.

【编校：许洁】

NumericalSimulationofTwo-DimensionalDrivenSquareCavityFlowBasedonStreamFunction-Vor⁃ticityMethod

LIJiangfei,LIYanfang,XIEDongmei,DUANXinghua,ZHANGKang,HUKai,LUGuoqiang,LIHonglei
(DepartmentofThermalEngineering,ChengdePetroleumCollege,Chengde,Hebei067000,China)

Combinediterationmethodwasusedtogaintheanalyticalsolutionoftwo-dimensionalsquareacvityflowby nondimensionalizedderivationanddiscreteofvorticityequation.BasedonMatlabprogramming,vortexstreamfunction methodsolvedtwo-dimensionalsquarecavityflow.Finitevolumemethodsolvedtheconservationequations.QUICK schemeandtwo-order-central-differenceschemewereappliedintoconvectionanddiffusiontermsseparately.Thedelay correctiontechniqueofdiscreteformatwasappliedintofinitevolumemethodforcalculation.Thedistributionofeach physicalquantitywasobtainedwhentheflowisinasteadystate.

numericalsimulation;cavityflow;vortexstreamfunction;finitevolumemethod

TB126

A

1671-5365(2015)12-0006-04

李江飞，李岩芳，谢冬梅，等.涡量流函数法模拟方腔内粘性不可压流动[J].宜宾学院学报,2015,15(12):6-9. LIJF,LIYF,XIEDM,etal.NumericalSimulationofTwo-DimensionalDrivenSquareCavityFlowBasedonStreamFunction-VorticityMethod[J].JournalofYibinUniversity,2015,15(12):6-9.

2015-07-06修回：2015-07-31

河北省科技支撑项目“采用电气液压调节的蒸汽透平机运行特性和节能分析”（13211609）

李江飞（1988-），男，讲师，硕士，研究方向为油气储运

时间：2015-07-3120:38

http://www.cnki.net/kcms/detail/51.1630.z.20150731.2038.001.html