基于超磁致伸缩效应的光纤电流传感器

王 志，初凤红，吴建平

(上海电力学院 电子与信息工程学院，上海 200090)

目前，电力系统中测量电流应用比较广泛的是基于电磁感应的电流互感器，该类互感器结构简单可靠、寿命较长、便于维护、价格较低，但也存在磁饱和、铁磁谐振、频带窄、动态范围小、有油易燃易爆等问题，[1]并且质量较大，精度较低.而光纤电流传感器(Optic Current Sensor，OCS)具有绝缘性好、安全可靠、抗电磁干扰、频带宽等优点，大有取代传统电磁式互感器的趋势.

本文研究的基于超磁致伸缩效应的OCS，避免了基于法拉第磁光效应类OCS受光纤本身双折射的影响，具有测量准确、线性度好、简单易行、可远距离操作等特点，只要控制好温度的影响，就可以得到很好的线性实验结果.

1 传感基本原理

实验中使用的光纤布拉格光栅(Fiber Bragg Grating，FBG)相当于在光纤的纤芯中嵌入一个频率很窄的反射镜或者滤光器，其反射谱或透射谱的中心波长与FBG自身的折射率调制周期和纤芯折射率两个因素有关，而这两个因素又会受到外界温度或者应力的影响.也就是说，如果控制好温度使系统处于恒温中，那么系统将不受温度的影响，FBG反射谱或者透射谱的中心波长将仅受应力的影响.

磁致伸缩效应是指磁性材料在外加磁场作用下，沿磁化方向发生伸长或者缩短的现象.而超磁致伸缩材料(Giant Magnetostrictive Material，GMM)因具有大的伸缩系数、高机电耦合系数，以及很好的稳定性和无疲劳等优点而成为换能领域应用最为广泛的器件.因此，利用GMM感应通电导体产生的磁场就会有很高的灵敏性、可靠性和稳定性，将GMM与FBG牢固地粘合在一起组成传感头，就可以实现电信号到光信号的转变.FBG中心反射波长可以表示为:[2]

式中:λB——入射光中心波长，也称为布拉格波长;

neff——栅区纤芯的有效折射率;

Λ——FBG栅格周期.

当受到应力和温度的影响时，FBG中心反射波长的漂移量ΔλB与入射光波长的关系为:[3]

式中:Pe——光纤的有效弹光系数，只与光纤材料有关;

ε——轴向应变;

α，ξ——光纤的热膨胀系数和热光系数;

Δt——传感头所在位置温度的变化.

因此，当传感头处温度保持不变时，FBG中心波长的漂移量ΔλB将只与其所受的轴向应变ε有关，并且呈现良好的一次线性关系.也就是说，如果能找到一段区域，恰好使得传感头所处磁场强度H与所受应力也呈一次线性关系，则最终电流大小必然与FBG中心波长的漂移量也呈一次线性关系，这样就可以实现直流电流的测量.

2 试验系统分析

整个实验系统由光源、光谱仪、3 dB耦合器和传感头组成，其系统框架如图1所示.

图1 实验系统框架

图1 中，光源采用宽带ASE光源，产生1 550 nm的中心波长;FBG由西安远哲光电有限公司提供，其中心波长为1 550 nm;GMM棒为TbDy(FeM)n系列超磁致伸缩材料;FBG与GMM棒用快固型AB胶粘连.光源发出的光经过3 dB耦合器到FBG+GMM传感头，然后反射回来并显示在光谱仪上，通过观察光谱仪中心波长的漂移量就可以推测出对应电流的大小.

当导体中通过电流时，会在导体周围产生磁场，并且磁场与通过的电流存在一次线性关系.实验采用螺线管来模拟大电流产生的磁场，螺线管中心产生的磁场与所加电流大小的关系为:[4]

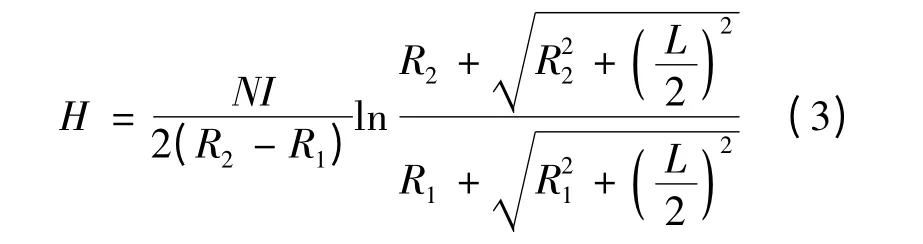
式中:I——通过螺线管的电流;

R1，R2——螺线管的内径和外径，实验中，R1=13 mm，R2=26 mm;

L——螺线管的长度，实验中L=66 mm;

N——螺线管所绕线圈的匝数，N=1 400匝.

由此可得该实验螺线管中心磁场强度与电流之间的关系为:

而对于多层轴向对称的螺线管，沿着轴向离线圈中心为z点处磁场强度可表示为:[5]

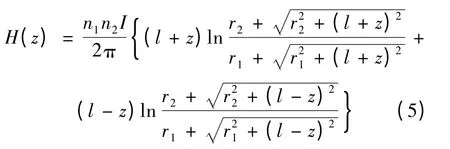
式中:n1——轴向单位长度的匝数;

n2——径向单位厚度匝数;

l——线圈轴向长度的1/2.

将上述螺线管的相关数据代入式(5)中，将式中的n1n2I/(2π)看作常数并规定其值为1.用Matlab软件进行仿真，得到GMM棒中心(z=0)到棒末端(z=25 mm)磁场大小分布如图2所示.

棒末端磁场强度为中心强度的84.8%，而光纤布拉格光栅(长度10 mm)所在区域磁场强度达到中心强度的95%以上，基本满足实验条件.

根据天星稀土功能材料有限公司提供的数据，并通过查阅相关资料可知，在无外加应力作用下，该系列超磁致伸缩棒GMM所受应力与外加磁场关系如图3所示.[6]

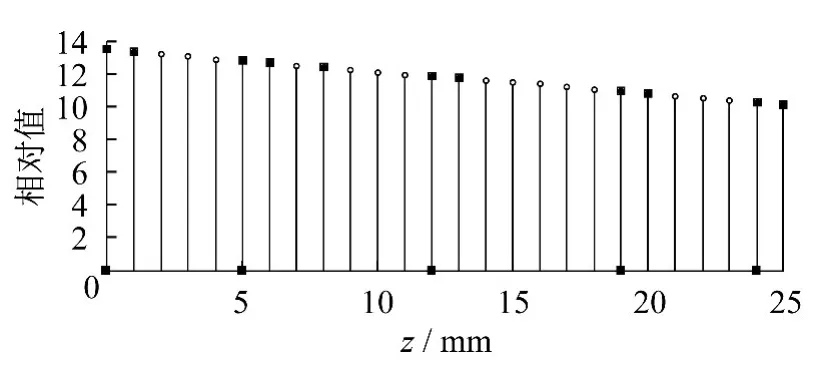
图2 棒中心到棒末端磁场大小分布

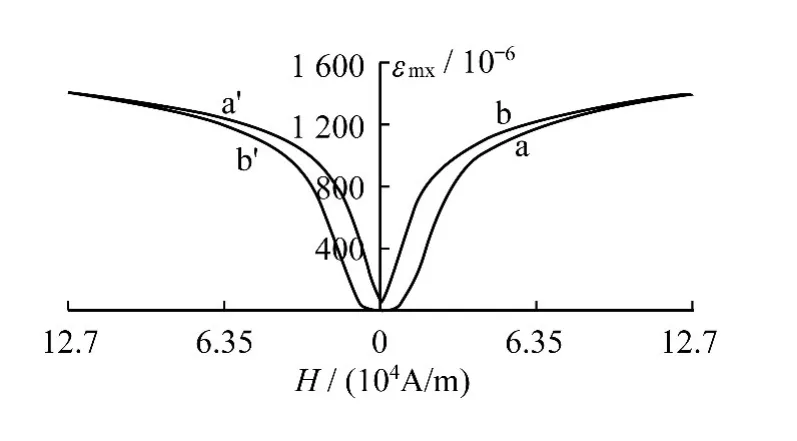
图3 零预加应力下所受应力与磁场关系

取图3的线性区域，即:

式中:k≈4.386×10－8m/A.

对于由SiO2制成的光纤，有效弹光系数Pe=0.221 260 08，若温度保持不变，即 Δt=0，则由式(2)、式(4)和式(5)可知，FBG中心波长漂移量ΔλB与其中心波长λB之间的关系为:

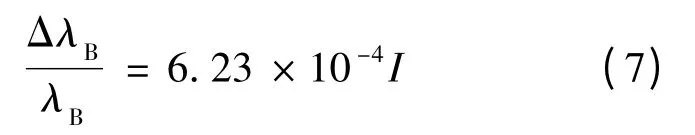
3 实验结果分析

将光源中心波长调至1 550 nm并保持输出功率为6.61 mW，电源电压稳定在2.0 V，电流由零逐渐增加，观察光谱仪上中心波长的变化.当电流为零时，测得中心波长为1 547.74 nm，随着电流的增加，所得实验结果如表1所示.

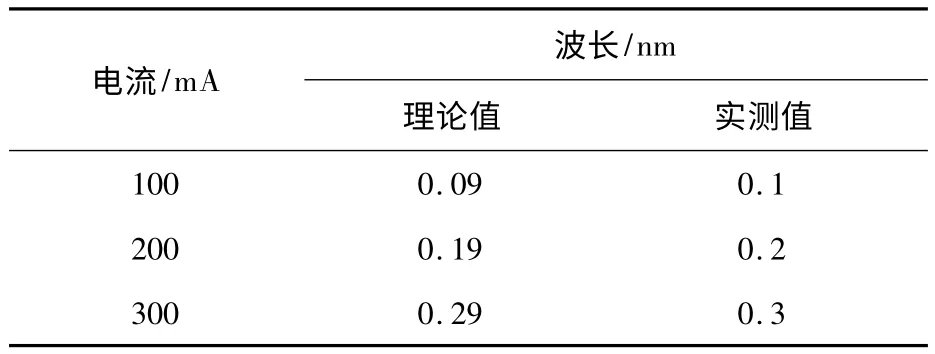
表1 通电电流与波长变化关系

用origin软件绘制实验结果并进行一次线性拟合所得曲线如图4所示.

对上述实测数据进行一次线性拟合，所得曲线的线性拟合度为:R2=(0.999 68)2=0.999 36;线性度误差为:δ=(6.46×10－4)%.

图4 理论值与实测值对比曲线

4 结语

由实验可知，通电电流值与中心波长的漂移量表现出良好的一次线性关系，即论证了基于超磁致伸缩效应制作光纤电流传感器的可行性.实验中光谱仪的分辨率为0.01 nm，故理论上该传感系统的灵敏度约为9.7 mA/nm.虽然在实验中为避免温度对传感头的影响，采用在恒温室中并且给螺线管通电时间尽可能短以减少发热的方式，但仍不能避免温度对实验结果的影响，这也是理论值与实测值存在误差的主要原因.同时由图2可知，磁场在传感头区域的分布也不是恒定的，这样也会影响到光纤传感器的性能.因此，若要使该传感系统走向实用化，一方面要做好温度补偿方面的研究，另一方面还应该改进螺线管的结构.

[1]何剑，程林.电力系统运行可靠性最优控制[J].中国电机工程学报，2010，30(7):27-29.

[2]廖帮全，赵启大，冯德军，等.光纤耦合模理论及其在光纤布拉格光栅上的应用[J].光学学报，2002，22(11):1 340-1 344.

[3]饶云江，王义平，朱涛.光纤光栅原理及应用[M].北京:科学出版社，2006:3-21.

[4]赵凯华.电磁学[M].北京:高等教育出版社，2006:361-367.

[5]赵凯华，陈熙谋.电磁学[M].北京:人民教育出版社，1985:123-125.

[6]廖帮全，冯德军，赵启大，等.光纤布拉格光栅电流传感的理论和实验研究[J].光学学报，2002，22(9):1 092-1 095.