逆变器电压电流双环控制设计及研究

孙 静，曹 炜，苏 虎，杨道培

(上海电力学院 电气工程学院，上海 200090)

微网通常使用可再生能源以及能够提高能源利用效率的燃气冷热电三联供发电.为使微网具有更好的控制性能，微网中也普遍配置储能装置.上述装置通常使用逆变器将直流或其他频率的交流转换为工频交流后再接入微网，并对其输出电压、电流波形有较高要求.高质量的波形要求逆变器系统在保证稳态性能的同时，还要保证总谐波畸变率(即THD)尽可能的低.许多文献都采用电流P和电压PI的双环控制策略，但是此控制策略不能减小电流的稳态误差，THD相对较大，而且当系统出现大扰动或者短路情况时起不到限流的作用.[1-2]文献[1]基于状态空间理论提出了一种新的电流PI和电压PI的双环控制策略(即PI-PI);文献[3]对双PI控制系统直接离散化后利用极点配置的方法设置了控制系统参数，分析了在空载、满载、过载时PI-PI控制的时间响应;文献[4]基于状态空间算法在单相逆变器下对比分析了P-PI控制策略与PI-PI控制策略的THD和电流峰值.

本文首先对三相对称逆变器系统进行d-q轴完全解耦，然后将工程方法与bode图相结合，设计分析了PI-PI控制器的各个参数，使等效输出阻抗成感性.[5-6]时域仿真结果验证了该设计在负荷变动时能够保证系统的电压、总谐波畸变率在要求的范围内，从而改善了电压质量，提高了系统的稳态性能.此外，当微网系统发生短路时也能有效地控制短路电流.

1 逆变器及其控制系统

本文采用三相逆变器，其原理如图1所示，主要包括空间矢量脉宽调制(Space Vector Pulse Width Modulation，SVPWM)模块、LC 滤波器、双环控制模块等.

图1 逆变器及其控制系统示意

SVPWM算法简单且适合数字化实现，可以减少逆变器输出电压的谐波，提高对电压源逆变器直流供电电源的利用率.[7-8]

逆变器的输出电压会在开关频率处产生谐波，需要采用滤波器加以滤除.滤波器参数选为L=3 mh，C=1 500 μF，保证滤波电感上的压降不超过系统电压的3%.[9-11]

本文重点探讨电压电流双环控制模块的设计和参数设置.

2 电压电流双环控制模块设计

对于整个逆变电源系统，控制系统与主电路同样重要，只有这两部分相互配合，共同正常工作，才能构成高性能的逆变系统，输出较高质量的波形.本文的电压电流双环控制系统采用 PI-PI控制器，利用工程设计方法与bode图及阶跃响应曲线相结合的方式，对控制系统的参数进行设计.

2.1 双环解耦设计

本文所研究的abc三相逆变器数学模型是多输入多输出系统，为了有效调节逆变器输出的有功功率和无功功率，需要引入坐标变换，将abc三相模型转换到两相d-q坐标系下，但电压、电流在d轴和q轴间存在严重耦合.在电流解耦时，文献[12]和文献[13]经过分析计算，将d轴的电感电流耦合量ildωL叠加到q轴的电压上，以消除控制对象中d轴电感电流对q轴电压的影响;在电压解耦时，采用的是完全解耦法，[14]即将 uodωC乘上一个控制量 Q(S)，[12](其中 Q(S)满足 Q(S)/(Ls+r)=1)，以消除控制对象中d轴电压对q轴电流的影响.由于d轴和q轴是对称的，q轴的电压、电流对d轴电流、电压的影响亦用此方法解耦.

2.2 双环控制参数的设计

电压电流双环控制均采用PI-PI控制器，如果按常规方法设计其参数，需考虑两个控制器之间的响应速度、频带宽度的相互影响与协调等，控制器设计步骤复杂，还需要反复试凑验证.因此，本文的电流内环采用工程设计方法以降低计算的复杂性，电压外环采用频域bode图与阶跃响应相结合的方法以减少实验过程中反复试凑验证的次数.

2.2.1 工程设计算法原理

工程设计算法一般是用系统的开环传递函数来确定闭环系统的参数，使闭环系统具有良好的稳定性.一般来说，控制系统的开环传递函数为:

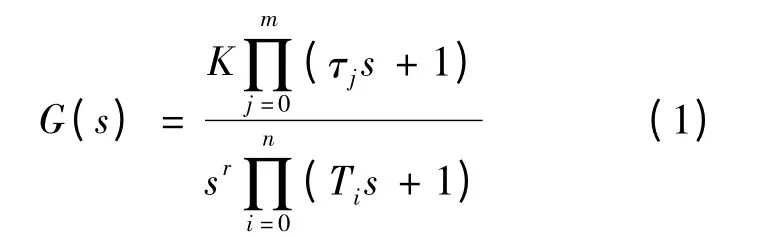
式中:K——开环增益;

τ，T——时间常数;

分母中的s——该系统在原点处有r重极点，根据 r=0，l，2，3…的不同数值，分别称作0型、1型、2型、3型……系统，为了保证稳定性和较好的稳态精度，多用1型和 2 型系统.[15]

典型1型系统的传递函数为:

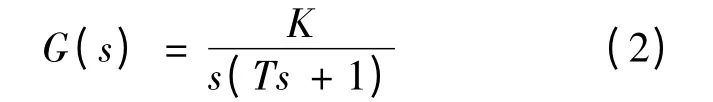
式(2)中有两个参数:开环增益 K和时间常数T，T是系统固有的，所以只要调节K，就可以调整系统的超调量与动态响应，一般取 K=0.5.[15]

典型2型系统的传递函数为:

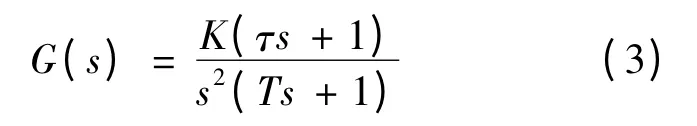
引入中间变量h:

式中:h——伯德图－20 db/dec的中频段的宽度.

由工程经验数据可知，h的取值应在2～10，当h变大时，系统的超调量会减少，但响应速度也会相应降低.如果既要保证系统的超调不会很大，又保证系统的快速性，可取h=5左右.

2.2.2 电流内环设计

很多文献中电流环都采用P控制器，但该控制器电流环存在稳态误差，而且在短路时起不到限流的作用.本文的电流环采用PI控制器，使其在保证响应速度、提高电流环控制精度的同时，在短路时还能起到限流的作用.

d轴和q轴进行完全解耦后，两轴均为对称的.将图1中逆变器、LC滤波器、SVPWM模块、电流环进行等效简化，d轴简化后的控制原理框图如图2所示.根据对称原理，相应的q轴原理图与其相仿.

图2的开环的传递函数模型可表示为:

式中:Kip——PI中的积分系数;

Ki——PI中的比例系数;

Ts——调制开关周期;

UDC——直流侧电压;

Kpwm——SVPWM 等效增益.

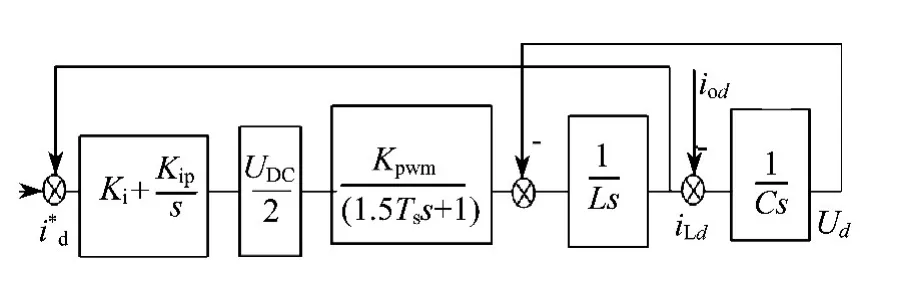
图2 电流环简化模型

由式(3)对比式(5)可知，电流内环的传递函数为2型.进一步对比式(3)和式(5)，并且引入式(4)可得:

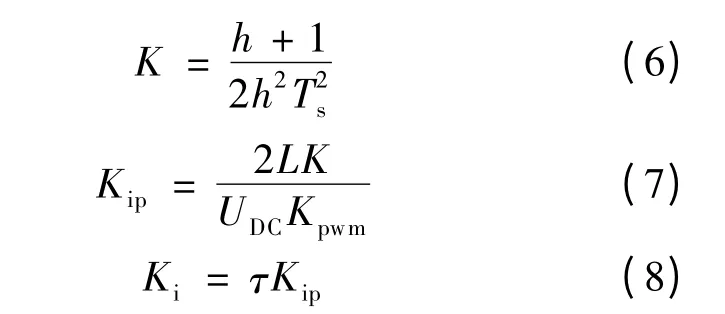
由于 h，Ts，L，UDC，Kpwm，τ 均为已知，将这些已知参数代入式(6)、式(7)和式(8)，即可确定电流环PI控制的积分系数 Kip和比例系数Ki，但由于采用了经验数据，且在系统传递函数的计算过程中存在简化环节，因此在后续仿真中需要对参数进行优化和系统性能校核.

2.2.3 电压外环设计

本文的电压环采用的是PI控制器，使逆变器输出电压为设定值.将图1中逆变器、LC滤波器、SVPWM模块、电流环、电压环进行等效，则电压环的模型框图如图3所示.

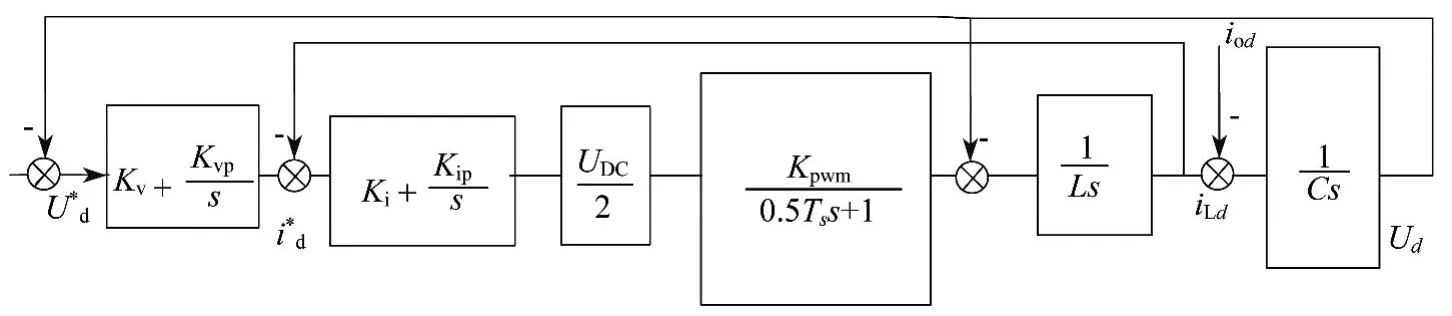
图3 电压电流环控制示意

图3电压环的闭环传递函数为:

式中:

Ud/iLd的等效输出阻抗为:

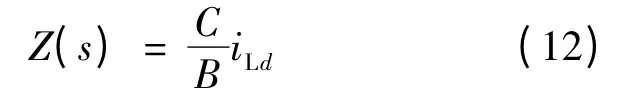
式中:

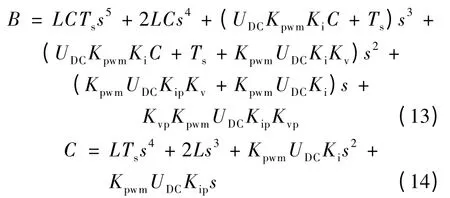
式(9)中的电压增益系数K1体现了系统对电压设定值的跟踪性能，等效输出阻抗Z(s)体现了电流对控制系统输出扰动特性.

3 PI-PI控制系统参数优化

虽然根据上述方法可以对双环控制器的参数进行理论计算设置，但还需要对控制器的动态性能进行多方面的考察，以使控制器达到更好的性能水平.本文对系统的参数设置如下:直流侧电压UDC为 500 V;滤波电感 L为 3 mH;电容 C为1 500 μF，SVPWM 等效增益 Kpwm为 1，调制开关周期 Ts为 2 ×10－4s.

3.1 电流环参数的优化

将上述系统参数代入式(6)、式(7)和式(8)，即可确定电流环参数 Kip=16，Ki=12.为了进行电流环参数的优化，当 Kip=16，Ki取不同数值时，电流环性能数据如表1所示.

仿真结果表明，当Kip=16，Ki分别取不同的数值时，相位裕量的取值范围为17～35，穿越频率的取值范围为 103.35～ 103.7，超调量的取值范围为 13% ～16.5%，响应时间为 0.6 ×10－3～1.5 ×10－3s.综合考虑后，选取 Kip=16，Ki=20 作为电流内环的参数，这样既可以提高响应速度，又可以保证系统的稳态性能.

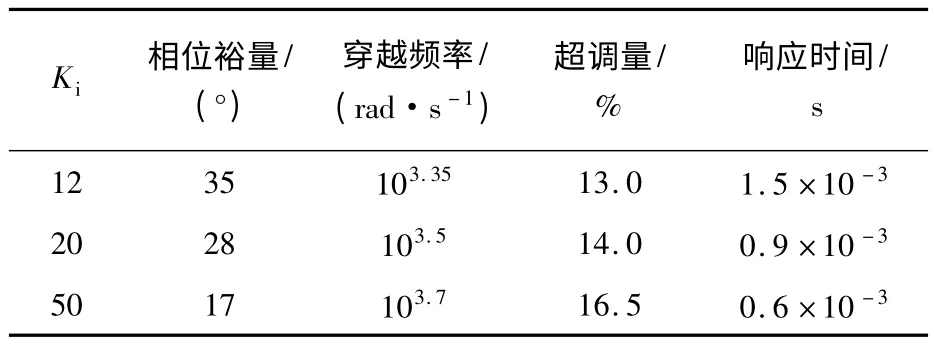
表1 电流环动态性能数据

3.2 电压环参数的优化

根据电流内环优化参数 Kip=16，Ki=20及式(12)、式(13)和式(14)，通过阶跃响应曲线及其bode图确定参数Kv和Kvp，仿真结果如图4所示.

图4 电压环动态性能

图4 a表明，当Kv=2，Kvp=7时系统的震荡、超调都很大，系统响应速度慢;但当 Kv≥15，Kvp=7时系统的超调降低，响应速度变快，因此系统的Kv应取大于等于15的数值.此外，当Kvp≥7时，bode图在50 Hz时等效输出阻抗接近感性.经过不断试验验证，当Kv=15，Kvp=7时，系统达到最佳状态，超调量＜15%，此时稳态性能好，响应速度快.

4 逆变器供电系统性能时域仿真验证

4.1 系统稳态性能和电压质量仿真

分别将电压电流双环PI-PI控制器和P-PI控制器置于用Matlab/Simulink搭建的图1所示逆变器供电系统中，分别在额定负荷(30 kW)、突加无功负荷、有功负荷、综合负荷4种情况下，分析系统的稳态性能与电压质量.PI-PI控制系统与P-PI控制系统的d轴和q轴参考电压分别为:系统双环控制参数为Ki=20，Kv=15，Kvp=7;P-PI系统的双环控制参数为:Ki=5，Kv=10.仿真结果如表2所示.

由表2可知，PI-PI系统比P-PI系统的稳态性能更好，电压质量也更高.

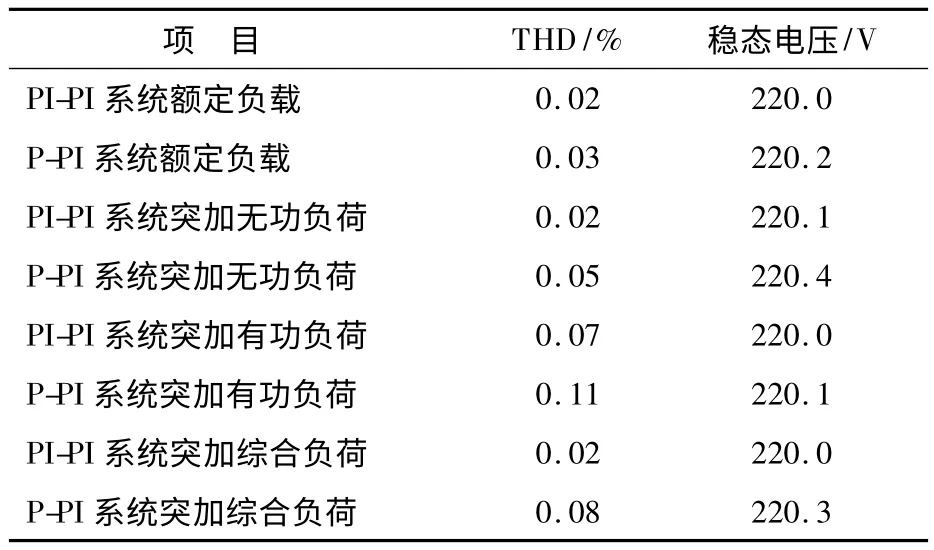
表2 THD及稳态电压对比

4.2 自限流功能

当负荷突然加大或者出现短路情况时，在PIPI双环控制器加入限幅环节后能起到限流作用，保证换流装置不被损坏，其对应框图如图5所示.P-PI控制器即使在对应位置加入限幅环节也不具有此功能，仿真结果对比如图6所示.

图5 加入限幅环节的双环控制

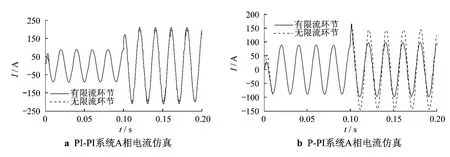
图6 自限流功能对比情况

图6 a为在0.1 s时系统短路，PI-PI系统加入限幅环节和无限幅环节，在短路的瞬间都出现很大的电流，但加入限幅环节后能非常快地将电流限定在规定的范围内(允许的最大电流值为100 A);而图6b显示在0.1 s时系统短路，即使加入限幅环节，P-PI双环控制下的输出稳态电流也远超限定电流100 A，幅值约在200 A.

5 结论

(1)利用工程算法与bode图、阶跃响应相结合的方式，快速地确定了PI-PI控制器参数.

(2)分别对电压电流双环 PI-PI控制器和P-PI控制器构成的逆变器供电系统用 Matlab/Simulink进行了时域仿真验证，仿真结果表明，PI-PI控制系统减少了电压误差，降低了逆变器输出电压的THD，而且该系统还具有限流功能，当出现大电流时能将电流值稳定在规定的范围内，保护逆变器的供电系统不被损坏.由此表明，PI-PI控制系统的性能优于 P-PI控制系统.

[1]彭力.基于状态空间理论的PWM逆变电源控制技术研究[D].武汉:华中科技大学，2004.

[2]张淳.含逆变型分布式电源的微网控制策略研究[D].杭州:浙江大学，2013.

[3]王淑慧，彭力.基于状态空间的溯逆变器的数字双环控制方法研究[J].电力电子，2008(5):44-50.

[4]何俊，彭力.PWM 逆变器双环控制研究[J].通信电源技术，2007，32(25):2-8.

[5]肖朝霞，王成山，王守相，等.微网分布式电源逆变器的多环反馈控制策略[J].电工技术学报，2009，24(2):100-107.

[6]王成山，高菲，李鹏，等.低压微网控制策略研究[J].电机工程学报，2012，32(25):2-8.

[7]张纯，陈民轴，王振存，等.微网运行模式平滑切换的控制策略研究[J].电力系统保护与控制，2011，39(20):1-6.

[8]肖朝霞.微网控制及运行特性分析[D].天津:天津大学，2008.

[9]杨淑英，张兴，张崇巍.基于下垂特性的逆变器并联技术研究[J].电工电能新技术，2006(2):34-40.

[10]艾欣，金鹏，孙英云，等.一种改进的微电网无功控制策略[J].电力系统保护与控制，2013，41(7):147-155.

[11]杨秀，藏海洋，宗翔，等.微电网分散协调控制策略设计与仿真[J].华东电力，2011(11):24-30.

[12]胡媛媛.三相三线逆变器数字控制系统研究[D].武汉:华中科技大学，2008.

[13]赵巍.微网综合控制技术研究[D].南京:南京理工大学，2013.

[14]CHANDORKAR M C，DIVAN D M，ADAPA R.Control of parallel connected inverters in standalone ac supply systems[J].IEEE Trans. on Industry Applications，1993，29(1):136-141.

[15]陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社，2003:120-150.