基于ANSYS软件的油浸式变压器温度场有限元仿真计算

薛 飞，陈 炯，周健聪，李 忠

(1.上海电力学院 电气工程学院，上海 200090;2.国网四川省电力公司 资阳供电公司，四川 资阳 641300)

随着电力建设的不断推进，电力设备朝着大型化方向发展，但大型变压器的内部温升控制问题一直是近年来困扰电网运行部门的技术难题之一.《GB/T 1094.7—2008油浸式电力变压器负载导则》中明确指出:“绕组最热区域内达到的温度，是变压器负载值的最主要限制因素，故应尽一切努力来准确地确定这一温度值”.[1]当热点温度超过指定限值时，会加速绝缘老化，缩短变压器寿命，影响变压器的正常运行.因此，开发合适的温度场计算技术，准确计算绕组热点温度及位置是亟待解决的问题.

目前，计算变压器热点温度的依据一般是实验结果和实践经验，但其误差较大，不能反映最热点温度和变压器内部整个温度的分布，并且难以确定热点的准确位置.[2]因此，笔者从传热学和流体力学理论出发，结合强大的有限元分析软件ANSYS，建立了油浸式变压器的有限元分析模型，分析并计算了变压器稳态运行下的温度场分布，较为准确地定位出热点的位置.

1 发热及传热原理

1.1 变压器的热源

变压器内部的热量主要由损耗转化而来，包括绕组损耗和铁心损耗，可以表示为:[3]

式中:PT——总损耗;

PC——铁心损耗;

PL——绕组损耗.

绕组中的损耗包括直流电阻损耗、涡流损耗及杂散损耗等，其中直流电阻损耗占主要部分，可表示为:

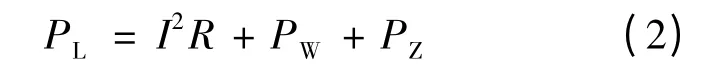
式中:I2R——绕组的电阻损耗;

PW——绕组中的涡流损耗;

PZ——杂散损耗.

铁心损耗主要由铁心中的磁滞损耗和涡流损耗构成，可以表示为:

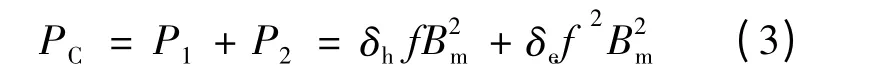
式中:P1——铁心中的磁滞损耗;

P2——铁心中的涡流损耗;

δh——磁滞损耗系数;

δe——涡流损耗系数;

f——电流频率，Hz;

Bm——磁通密度的最大值，Wb/m2.

绕组的涡流损耗和直流电阻损耗产生的热量直接作用于绕组，从而引起绕组温度升高，并且也是变压器内部热量的主要来源.

1.2 传热机理分析

对于油浸式变压器来说，运行中所产生的热量主要以传导和对流方式进行传递，其热量散失过程如图1所示.

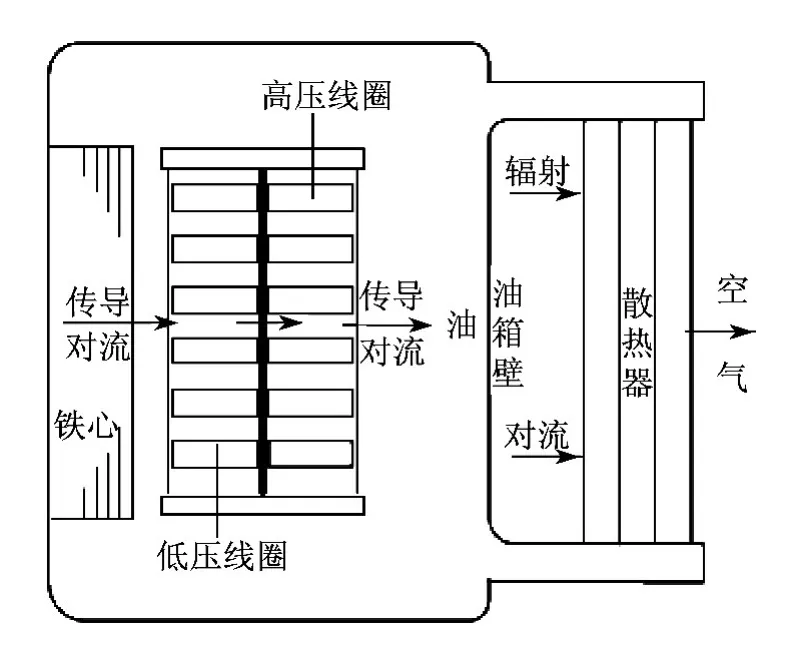
图1 变压器内部传热原理示意

热量的传递过程分为4个部分:一是铁心、绕组产生热量，经内部传导，热量传递到与油接触的外表面;二是外表面的热量经过对流传递到油，油温逐渐升高;三是变压器油向上流动，接触油箱壁，油温下降，油向下流动;四是冷油回到底部又重新流入绕组，形成了闭合的对流路线.油箱壁对空气的辐射传热可忽略不计.因此，热传递在变压器内部固体间表现为热传导，在固体与油之间表现为对流.

通过适当假设以及参照能量守恒定律可得出热传导的数学模型[4]假设如下.

(1)绕组为各向同性的连续介质.

(2)导体的密度、比热容和导热率均为常物性.

(3)导体内部有热源且均匀分布.qv为单位体积的生热率，V为导体体积，则qv=P/V.

所得微分方程式如下:

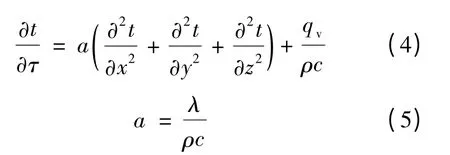
式中:a——热扩散率，即导温系数;

λ——导热系数;

c——比热;

ρ——密度.

在不考虑时变的稳态传热时，式(4)可简化为:

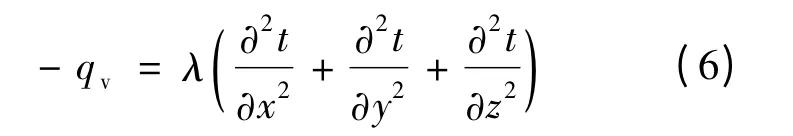
对流主要取决于对流换热系数、固体与油流温度差、换热表面积，实际工程中采用牛顿冷却公式:[2]

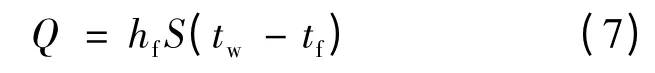
式中:hf——对流换热系数;

S——换热表面积;

tw——固体表面温度;

tf——油流温度.

由于对流过程中油的导热系数、比热及密度都是温度的函数，因此正确确定hf是计算变压器内部温度场的关键.[5]

2 ANSYS模型的建立

ANSYS软件是融合电场、磁场、温度场于一体的大型通用有限元分析软件.其强大的多物理场耦合计算功能使其在跨领域多变工程中得到广泛的使用.[6]ANSYS Workbench Environment(AWE)作为新一代多物理场协同 CAE仿真环境，集建模、有限元分析、优化设计3大模块于一体，为设计人员提供了系统级的解决方案.本文就是利用Workbench对油浸式变压器内部流固耦合的环境进行仿真分析.

2.1 确定边界条件及物性参数

本仿真过程为稳态求解，即发热和散热达到热平衡.固体所用的比热、导热系数及材料密度均为常数，油的物性参数采用拟合输入，见表1.热源密度为常数，环境温度及初始油温为20℃.

表1 变压器油物性参数

本文所模拟的油浸式变压器只考虑自然对流，并且忽略油箱壁对空气的辐射散热，因此用到两类边界条件，即第1类边界条件和第3类边界条件.

油与铁心、绕组及油箱壁之间是典型的对流换热，属第3类边界条件，满足:

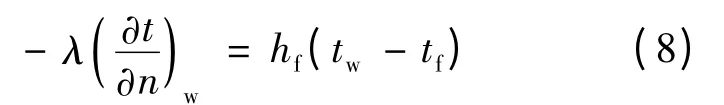
式中:λ——导热系数;

n——法方向.

由于油箱的几何形状比较规则，因此自然对流换热系数hf可取均值.

式中:Nu——努塞尔数;

此外，大峡谷村游客中心内部设置茶馆、餐厅、农特产与纪念品销售处、休闲娱乐区域等场所，由于布局、价格等原因，处于闲置状态。游客办理相关业务后，较少在游客中心停留，资源浪费直接影响游客中心运营，因此结合大峡谷村游客中心实际情况，可通过以下方式对消费场所进行整合利用。可将游客中心作为乡村单体旅游资源，将其设计为团队旅游路线的一部分，为游客提供团队餐、品茶、休憩、参观等活动。同时，团队旅游具有一定的规模，能够带动散客参与其中。

Ra——瑞利数，Ra=GrPr;

Gr——格拉晓夫数;

α——热膨胀系数，α =1/T;

β——运动粘度，m2/s;

H——特征尺寸，m;

Δt——温差，℃;

C，n——比热和法方向，数值由试验确定;

油流与绕组的对流散热比较复杂，由于各绕组的生热率、几何形状及空间位置都不同，使得它们与油之间的hf相差较大，不能采用均值.事实上，油流可分为层流和湍流，两者换热效果相差较大，可通过雷诺系数Re来判断:

式中:v——流体流速;

ρ——流体密度;

Lc——特征尺寸;

μ——动力粘度.

当Re＜2 300时，流动为层流，反之为湍流.

对于油箱壁面则用到了传热学中的第1类边界条件，即规定流体边界上的温度为常数20℃.

2.2 仿真模型及网格划分

本文所选变压器为三相对称，且各相关量的变化成轴对称，即温度场的分布在变压器内部沿圆周方向没有梯度变化，这里选用其中一相，作1/4三维轴对称圆柱体模型进行温度场计算.模型的参数如下:油箱尺寸为820 mm×800 mm×500 mm;铁心导热系数为40 W/mK;生热率为9 651.39 W/m3;绕组导热系数为336 W/mK;低压绕组平均生热率为28 954.17 W/m3;高压绕组平均生热率为12 578.81 W/m3.

网格划分的方式对分析结果影响较大，本模型为流固耦合模型，因此采用完全非结构化分段划分方法，[7]在耦合交界面以及温度梯度较大的部位网格较细，这样在保证精度的前提下又不至于过分影响系统的计算效率.网格划分后的局部模型如图2所示.

图2 模型上端部网格划分

2.3 程序计算流程

仿真计算流程如图3所示.需要注意的是，要先建立流体场分析模型，在此基础上再建立固体模型，添加材料属性和划分网格.计算结束后对每一次的计算结果进行收敛性以及精度的判断，当精度未达到要求时，返回修改流场参数及网格参数，然后再次进行迭代计算，直到达到足够精度为止.[8]

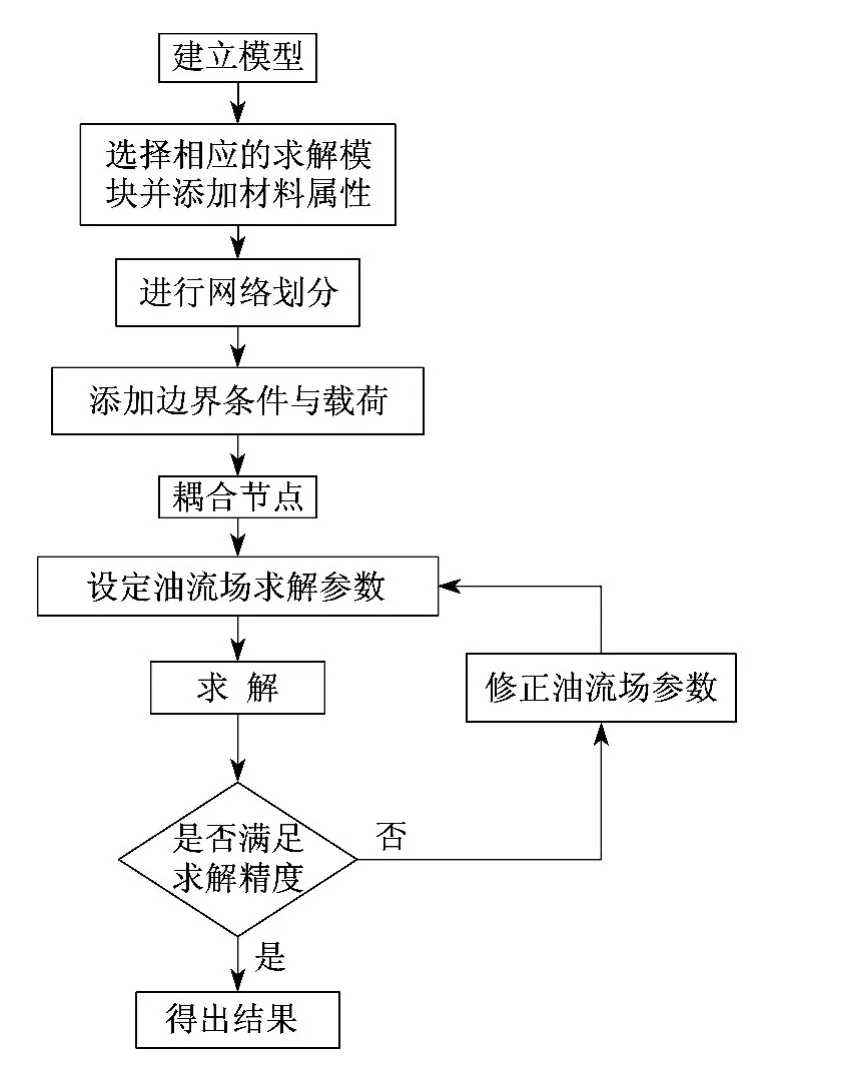
图3 仿真计算流程

2.4 仿真结果及分析

利用ANSYS软件计算了在环境温度20℃下，额定容量为2 500 kW且在额定负荷运行下的变压器的温度场分布情况，其轴截面温度场分布如图4所示.

图4 温度场分布

从图4可以看出，铁心及绕组的温度分布都不均匀，下部温度低，上部温度高;最低温度出现在铁心的下端部分，最热点则出现在低压绕组内侧轴向80% ～85%处，其温度为85.7℃，低于变压器所规定的参考温度98℃.[1]从传热学及流体力学的角度考虑，热量从绕组的内侧以一定的传导系数向外传热，在绕组表面与油接触后进行对流换热，沿轴向向上流动，因此要带走一部分热量;同时，绕组上端部散热效果比下端部差，从而使得上面温度高于下面温度;高压绕组在外层，散热效果比低压绕组好，因此温度低于低压绕组.

3 结语

本文采用ANSYS软件对油浸式变压器进行了建模与仿真，考虑油粘滞度随温度的变化及非线性的绕组发热功率，最后得到变压器内部温度场分布图，并结合传热学及流体力学的原理对所得结果进行了分析.经与经验测量结果及 IEEE推荐方法计算值对比发现，计算精度可满足工程要求，同时也为热点位置的定位提供了理论依据.

[1]中国电器工业协会.GB/T 1094.7—2008油浸式电力变压器负载导则[S].北京:中国标准出版社，1994.

[2]傅晨钊，汲胜昌，王世山.变压器绕组温度场的二维数值计算[J].高电压技术，2002，28(5):10-12.

[3]陈伟根，苏小平，周渠，等.基于顶层油温的变压器绕组热点温度计算改进模型[J].重庆大学学报，2012，35(5):69-75.

[4]曲德宇，刘文里，韩波.干式变压器绕组温度场的二维数值分析[J].变压器，2011，48(12):21-25.

[5]崔伟，张喜乐，李永刚，等.基于Fluent软件的干式变压器绕组热点温度计算与分析[J].电力科学与工程，2011，27(1):32-35.

[6]温波，刘爽，冯加奇，等.油浸式电力变压器绕组温度场的二维仿真分析[J].变压器，2009，46(9):35-38.

[7]杜莉，王秀春.油浸式变压器内流场和温度场的数值模拟研究[J].变压器，2012，49(1):19-22.

[8]李季，罗隆福，许加柱.电力机车主变压器油箱三维温度场有限元分析[J].高电压技术，2005，31(8):21-23.