矩形超磁致伸缩材料板内涡流密度的分布

刘会峰， 李俊林， 杨栋辉

(1.太原科技大学材料科学与工程学院，山西 太原 030024；2. 太原科技大学应用科学学院，山西 太原 030024)

超磁致伸缩材料是20 世纪70 年代发展起来的一种新型功能材料[1].超磁致伸缩材料因其具有磁致伸缩系数大、响应快、能量密度大、精度高等特点[2]而在传感器[3-5]、致动器[6-7]及换能器[8-10]等中有广泛的应用. 然而， 在外激励磁场作用下， 涡流不可避免地会导致输出功率的降低及器件的过度发热.

在过去的几十年， 旨在降低涡流损耗影响的研究已取得了许多成果. 一些学者致力于广泛应用在车削加工领域的棒状超磁致伸缩材料的研究[11-13]. 还有一些学者对超磁致伸缩材料板内磁场与涡流的研究是基于无限大薄板的[14-15]， 在这种情形之下， 可以把板看作是二维的. 但事实上， 许多情况下， 把板简化为二维的薄板是不合理的. 本文我们主要研究三维矩形超磁致伸缩材料板内的涡流分布情况， 此研究结果为合理选取材料参数降低涡流损耗提供了理论依据.

1 矩形超磁致伸缩材料板内部磁场强度

外磁场H0＝(0，0，H0z) ＝(0，0，Hsejωt) 作用于超磁致伸缩材料矩形板， 如图1 所示，2a，2b，2c 分别表示矩形板的长、宽及厚度.

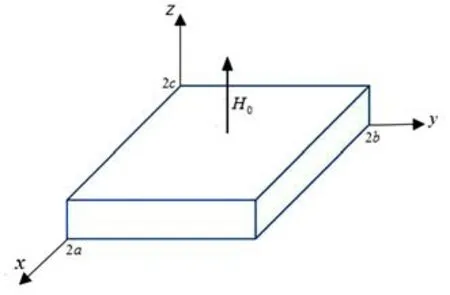
图1 外激励磁场作用于矩形超磁致伸缩材料板Fig.1 The rectangular giant magnetostrictive plate is placed in the external magnetic field

由Maxwell 方程可得， 矩形超磁致伸缩材料板内部磁场H(x，y) 可由以下方程确定[16]:

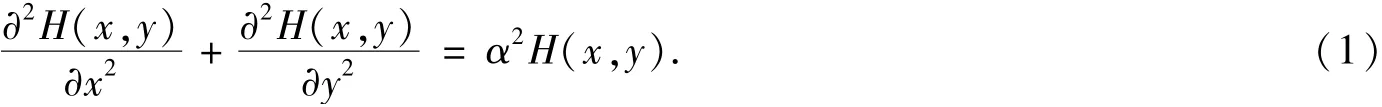
应用二重Fourier 正弦变换， 可解得

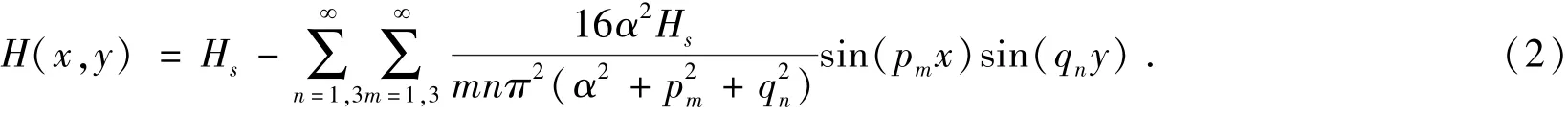
所以，t 时刻板内磁场强度为

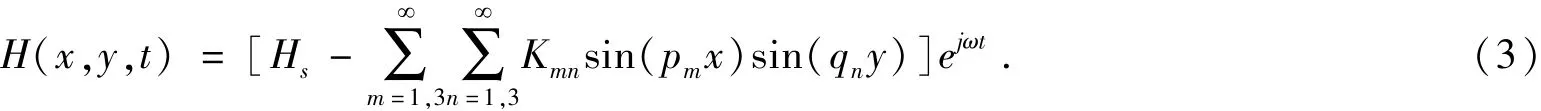
2 矩形超磁致伸缩材料板内部涡流密度

应用Maxwell 方程∇× H ＝J， 由上面的式(3)可得板内x 方向和y 方向上的涡流如下:

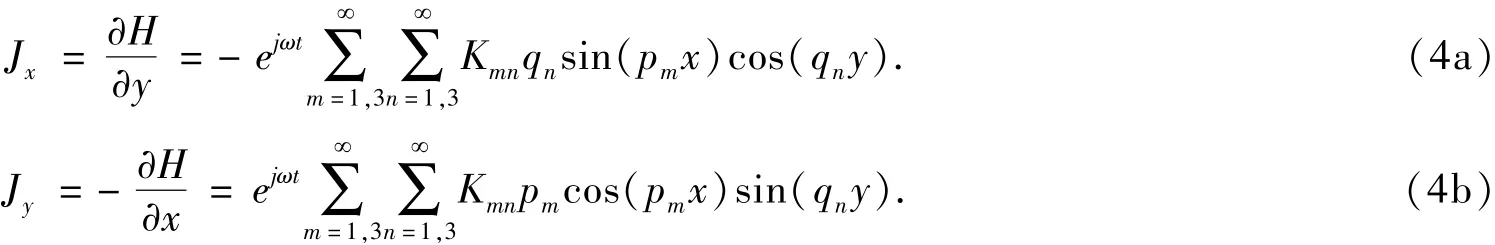
于是， 涡流密度即为:

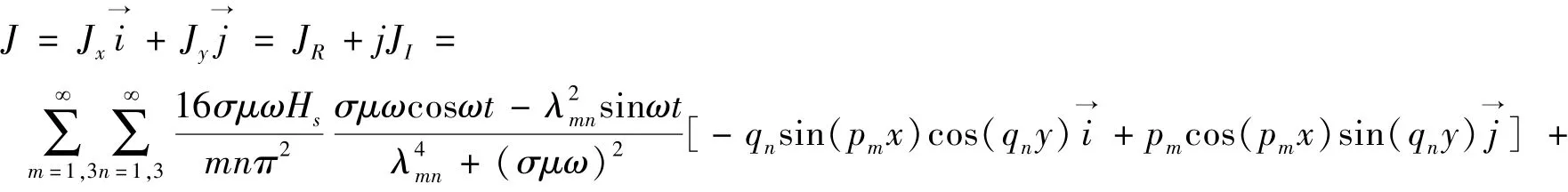
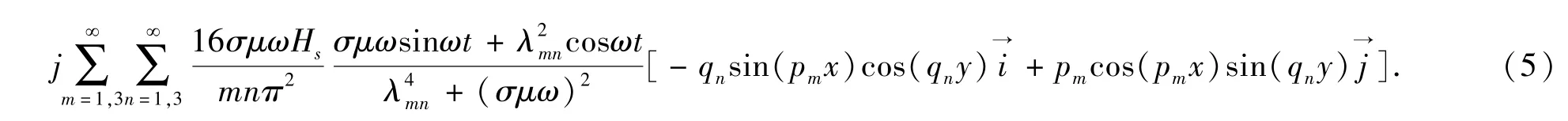
其中，

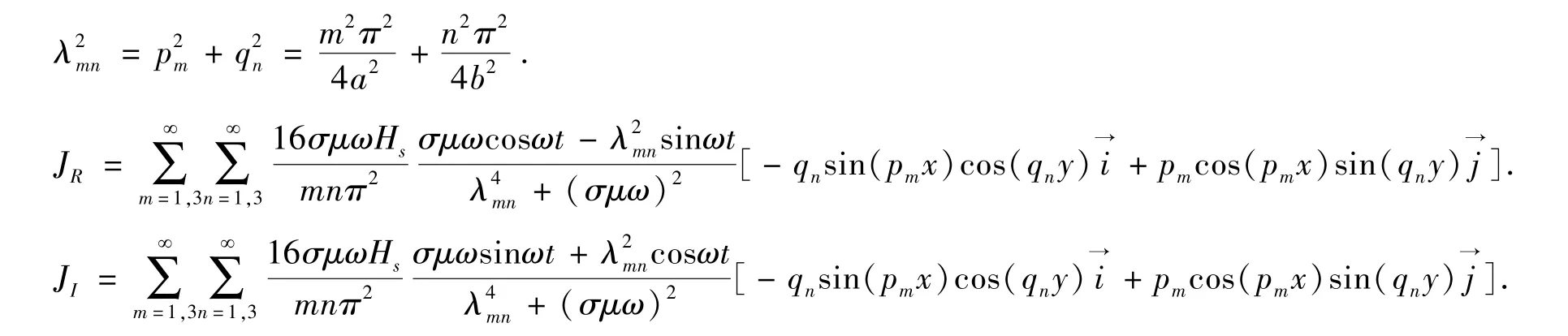
JR，JI分别表示涡流密度的实部与虚部； i→， j→分别表示x 方向与y 方向的单位向量. 所以，

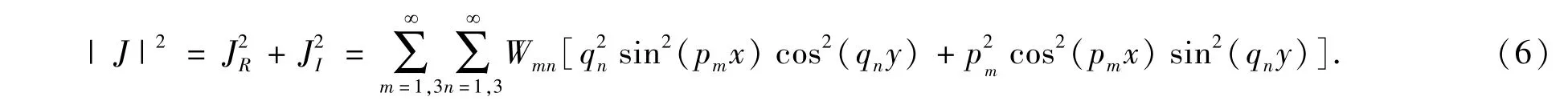
由此可得单位体积内涡流功率为:

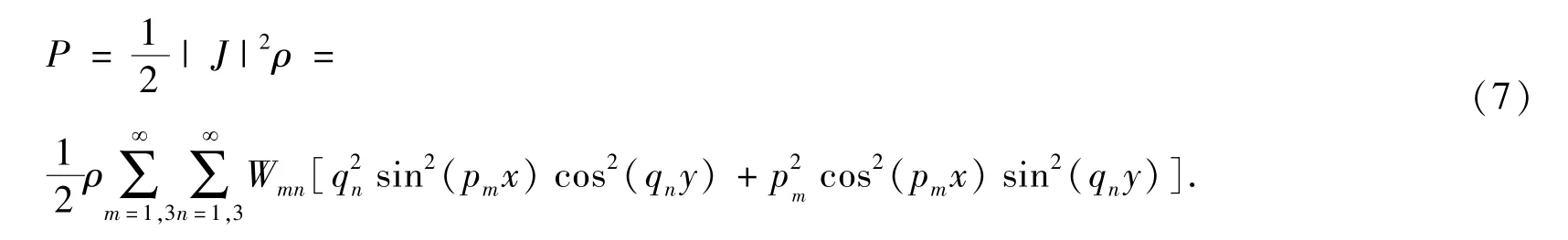
其中，ρ 为材料的密度.

所以， 整个板内每秒的涡流损耗为:

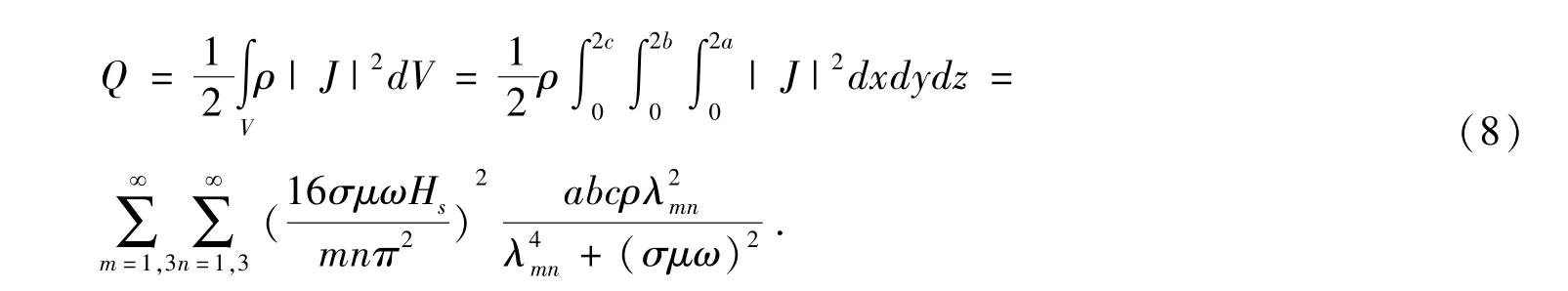
3 矩形超磁致伸缩材料板内涡流密度的分布

矩形超磁致伸缩材料板的参数如下取值:2a ＝0.005 m，2b ＝0.01 m，f ＝500 Hz，μ0＝4π ×10-7H/m，μr＝32 ，σ ＝1.667 ×106S/m，Hs＝500 A/m， 我们可得板内涡流密度的分布如下图2 所示:

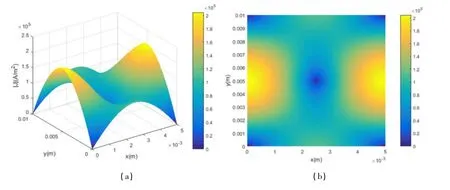
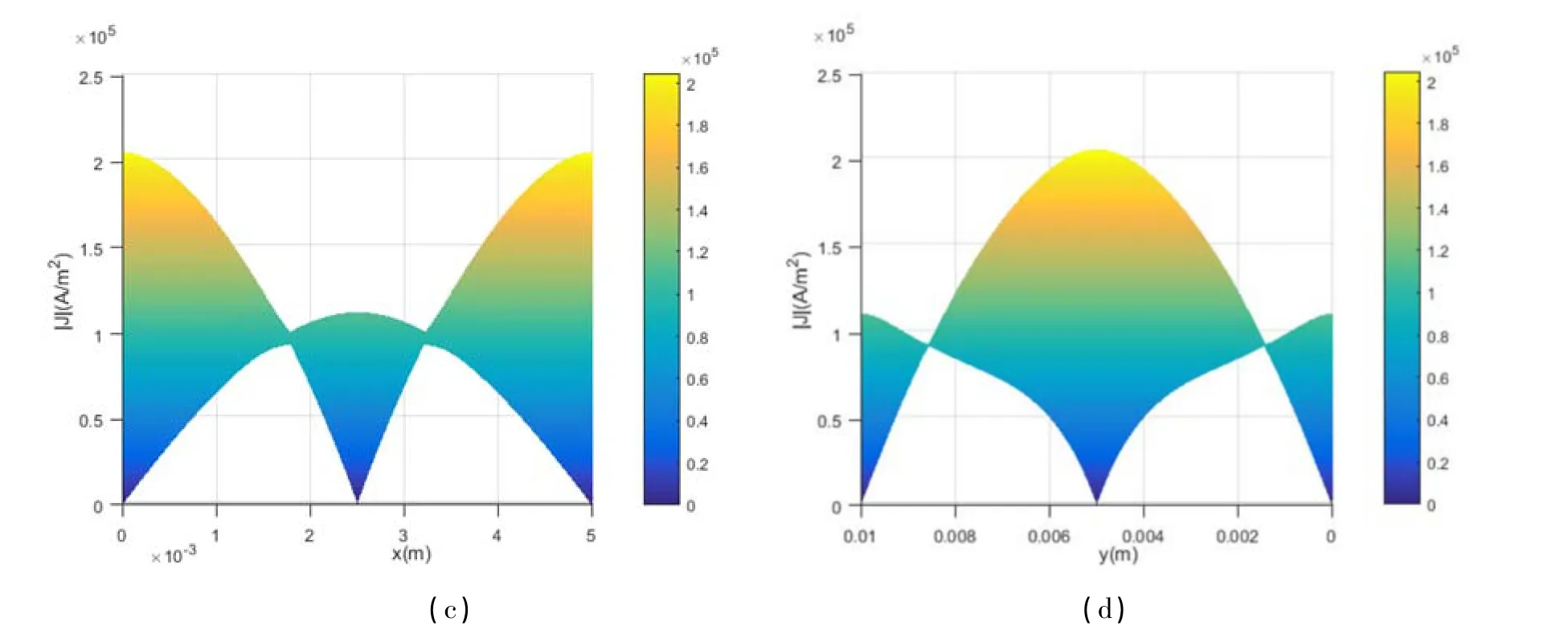
图2 矩形超磁致伸缩材料板内涡流密度分布:(a) 3D 视图； (b) 沿z 轴方向俯视图； (c) 沿y 轴方向视图； (d) 沿x 轴方向视图Fig.2 Distribution of eddy current density in rectangular magnetostrictive plates:(a) 3D view； (b) View along z-axis direction； (c) View along y-axis direction； (d) View along x-axis direction

图2 给出了涡流密度的3 维视图以及分别沿三个坐标轴方向的视图， 从图中可以看出， 涡流在板内呈轴对称分布， 以平行于x 轴与y 轴的板的两条中心轴线为对称轴. 涡流在板的中心部分减小并趋于零， 在板的中心， 即在(a，b) 处， 由涡流密度的表达式可以看出， 当x ＝a，y ＝b 时，

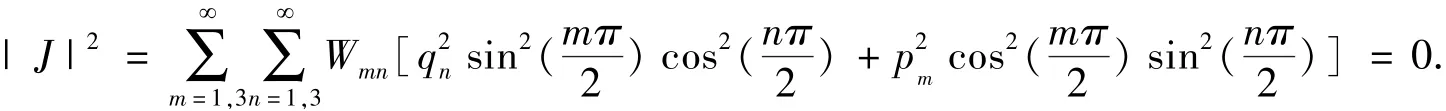
由此可知， 涡流的最小值取自板的四个边角及板的中心处， 且Jmin＝0 . 而涡流密度的最大值取自平行于y 轴(矩形板的长边方向)的两条边的中点， 平行于x 轴的(矩形板的短边方向)两条边的中点处涡流密度次之.特别地， 若板为正方形的， 则涡流密度为中心对称的， 其最大值取自四条边的中点.

4 板内涡流密度的影响因素

下面我们分别考虑外激励频率， 板的电导率及相对磁导率对板内涡流密度的影响.

当外激励频率分别取200 Hz、500 Hz、1 000 Hz 及1 500 Hz 时，板内涡流密度的分布如图3 所示. 由此可以看出， 随着外激励频率的增大， 板内涡流密度也在增大.

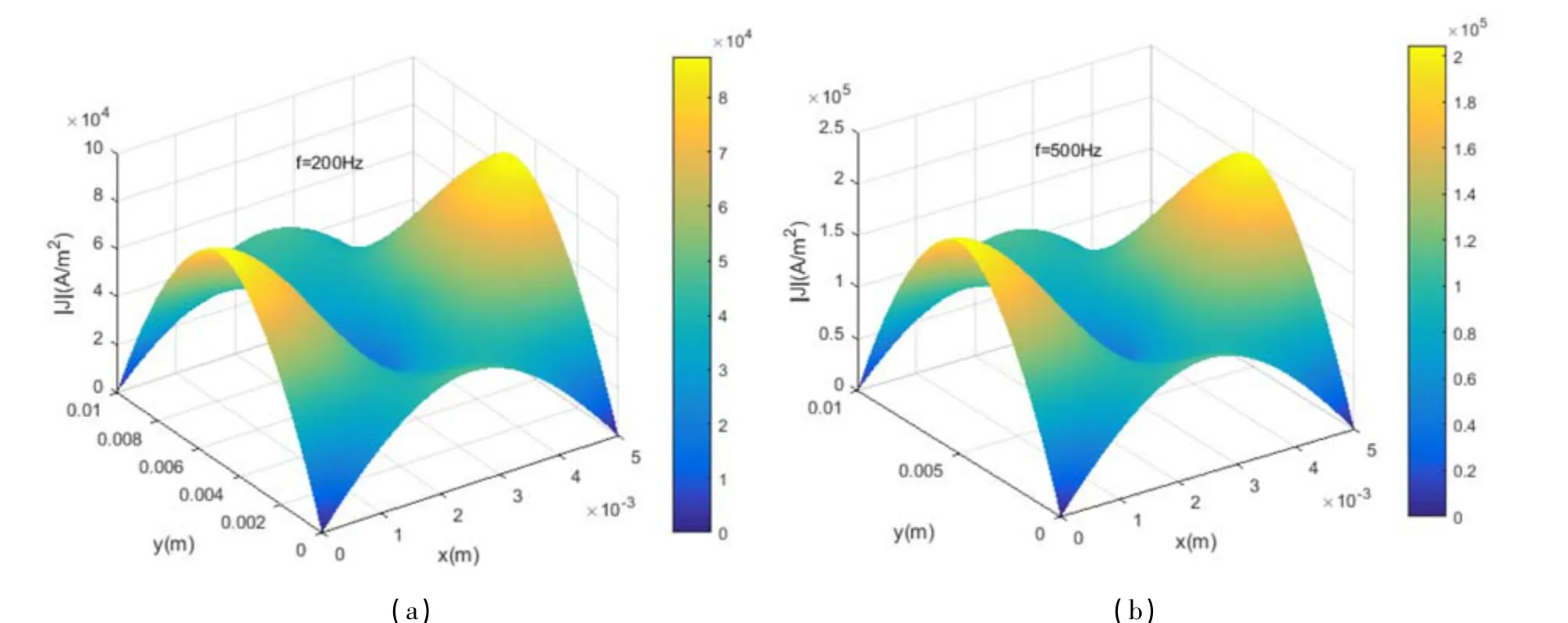
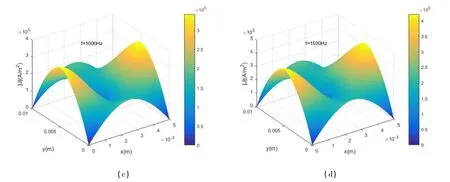
图3 不同外激励频率下矩形超磁致伸缩材料板内涡流密度的分布Fig.3 Distribution of eddy current density in rectangular giant magnetostrictive plate with different excitation frequency

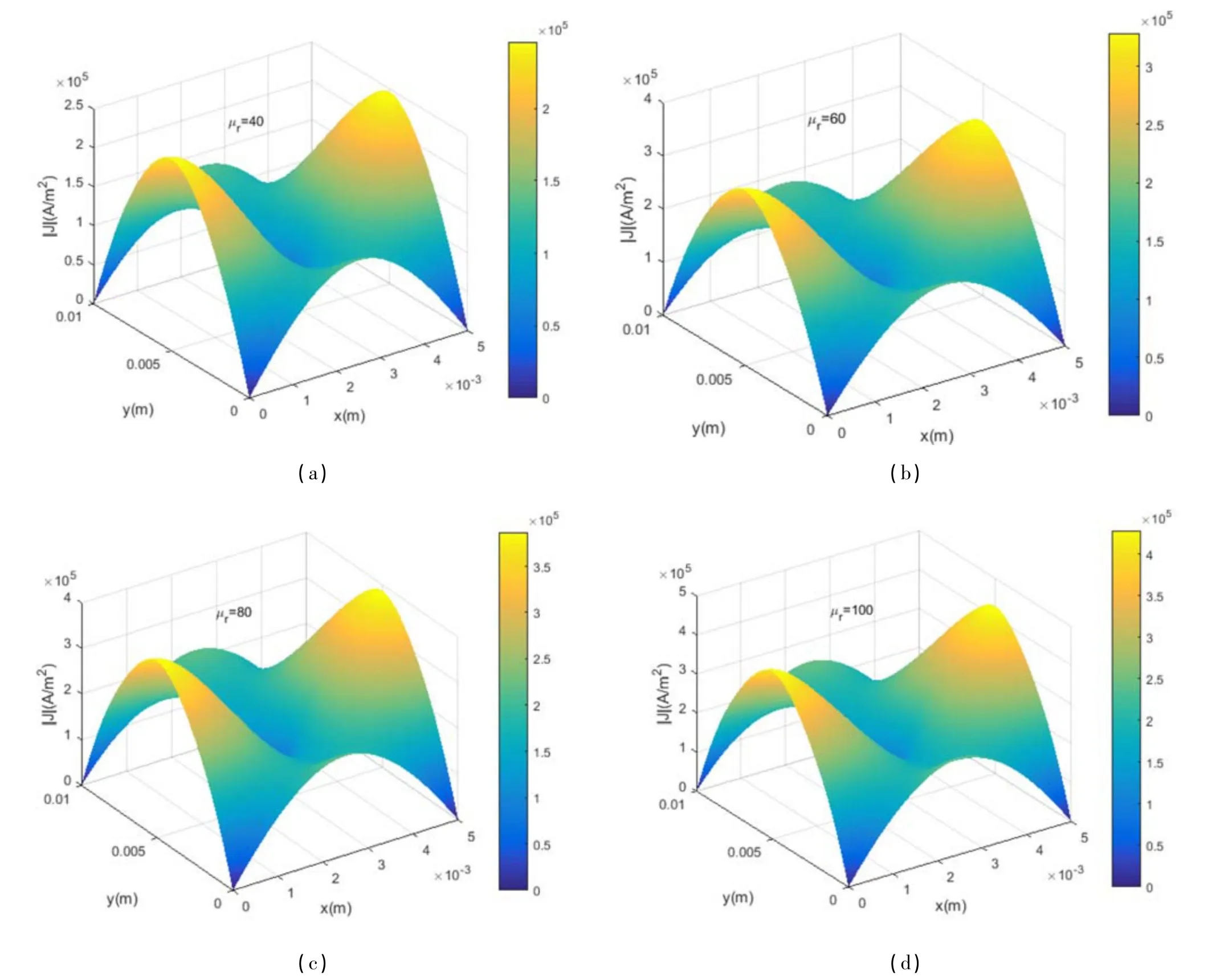
图4 不同相对磁导率下矩形超磁致伸缩材料板内涡流密度的分布Fig.4 Distribution of eddy current density in rectangular giant magnetostrictive plate with different relative permeability

图4 所示为当板的相对磁导率μr分别取40，60，80 和100 时板内涡流密度的变化. 由图可知， 当相对磁导率增大时， 涡流密度增大.

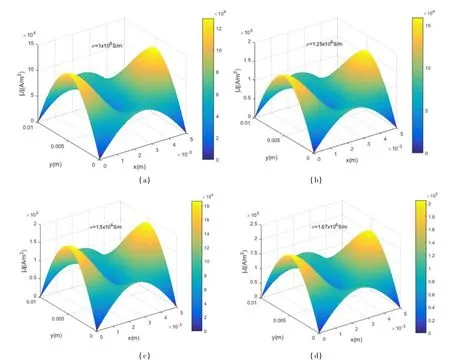
图5 不同电导率下矩形超磁致伸缩材料板内涡流密度的分布Fig.5 Distribution of eddy current density in rectangular giant magnetostrictive plate with different conductivity

图5 给出了当板的电导率σ 分别取1 ×106S/m、1.25 ×106S/m、1.5 ×106S/m 及1.67 ×106S/m 时板内涡流密度的变化情况. 可以看出， 随着材料电导率的增大， 板内涡流密度也增大.

5 结论

1) 基于由双重Fourier 级数表示的矩形超磁致伸缩材料板内磁场函数所计算得到的板内涡流密度函数表达式， 在理论上能较好地反映矩形板内涡流密度的分布.

2)通过对超磁致伸缩材料板内部涡流密度分布的分析， 得出涡流密度不仅与板的形状有关， 还受外激励频率、材料的电导率及相对磁导率的影响.

3)外激励频率、材料的电导率及相对磁导率分别增大， 板内涡流密度也随之都增大.