基于分类解耦模糊PID 控制的倒立摆系统

吕 志

(商丘师范学院 物理与电气信息学院，河南 商丘476000)

倒立摆系统是一种典型的多变量、非线性、强耦合和快速运动的自然不稳定系统［1］。对于这样一个复杂系统各国学者做了大量的研究工作，从理论上涉及到系统控制中的许多关键问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等［2－5］。

以倒立摆系统为研究对象，通过对数学模型分析，采用一种分类解耦的线性化方法。随着理论的发展，模糊PID 控制算法作为一种非线性智能控制方法，已在多变量、非线性等复杂系统的控制中发挥了重要的作用，为此文中将模糊PID 控制应用于倒立摆系统中，最后通过Matlab 仿真证明该设计方案的有效性与优越性。

1 倒立摆系统模型及其线性化

如图1 所示，将倒立摆系统看作为小车和匀质杆件组成的系统。根据其结构和动力学原理，可以建立倒立摆系统的数学模型［6－9］。

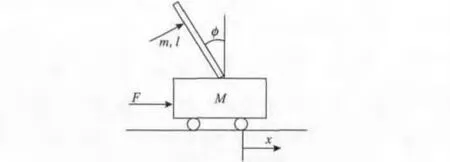
图1 倒立摆系统原理示意Fig.1 Diagram of inverted pendulum system principle

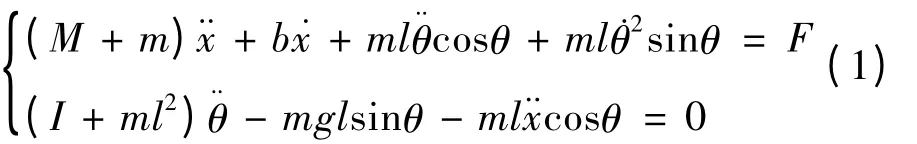
其中，小车质量为M，摆杆质量为m，在小车上的控制力为F，摆杆转动惯量为I，摆杆转动轴心到杆质心长度为l，x 代表小车位移，φ 代表摆杆与竖直向上方向的夹角，小车的摩擦系数为b，重力常数g;且有摆杆摆角θ = π + φ。

由于研究该系统的主要目的是使倒立摆在外力的作用下小车上的摆杆仍然保持目标状态，即竖直向上的状态，所以摆杆产生的摆角幅度较小，为此认为:φ ＜＜1，则有如下关系近似成立:cosθ ≈－1，sinθ ≈θ，˙θ2≈0，带入上式方程可得式(2):

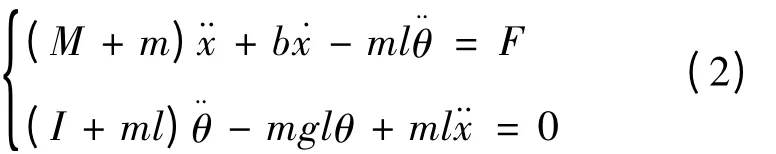
由方程(2)可以看出，该系统有4 个输入变量即为(˙x，x，˙θ，θ)，将式(2)整理为矩阵形式可以得到式(3):

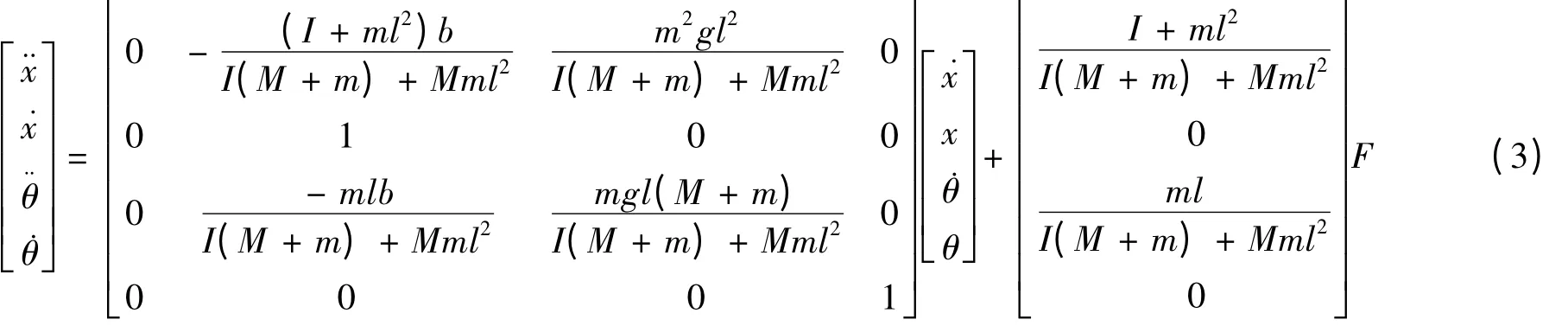
由式(3)可见，系统中变量、位移x 与摆杆摆角θ 之间存在一定的耦合关系，不能直接实现闭环控制，所以先对变量进行线性化解耦。在解耦的过程中，考虑到输入变量为位移与速度两大类，属于二维变量。为了便于实现控制，对控制变量进行分类解耦，具体方法是将式(3)中¨x，θ¨参数进行转换，即可得到式(4)。式(4)实现了对系统变量的线性化解耦。

为此，系统中变量位移x 与变量摆杆摆角θ 之间的耦合关系通过式(4)分类解耦实现了线型处理，从而可以分别对其设计模糊PID 控制器，不必担心2 个变量间的互相干扰问题。

2 模糊PID 的控制器设计

如上所述，倒立摆系统是一个多变量、非线性、强耦合不稳定的高阶系统，其系统的控制目标是系统在外力的干扰下摆杆仍然保持竖直向上的状态。然而，根据该系统自身的特点，即在对倒立摆摆杆角度进行控制的同时，还应对倒立摆系统的小车位置进行辅助控制，因此提出摆角与位置分类解耦控制。

为了最简单化的实现目标控制，文中在变量分类解耦的基础上，提出基于分类解耦模糊PID 控制方案，即在经典控制理论算法上，建立其模糊控制规则，然后再通过对倒立摆系统误差及误差变化率的计算，最终实现对倒立摆系统PID 参数的最佳调整。其结构如图2 所示。

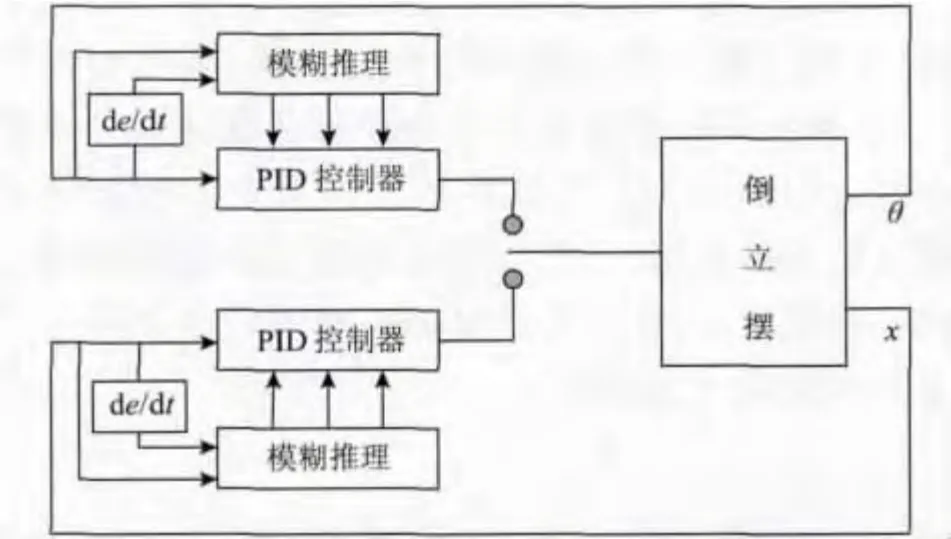
图2 分类解耦模糊PID 控制结构Fig.2 Structure diagram of classification decoupling fuzzy PID control

模糊自整定PID 控制器以误差e 和误差变化率˙e 作为输入，PID 参数kp，ki，kd 作为输出。根据前面的分类解耦，已将系统的4 个输入变量转化成两个独立的两输入三输出的变量系统。在此只需设计两个模糊控制函数即可。这里将误差和误差变化率作为模糊控制器的两个输入、输出分别为摆杆摆角与小车位移。

文中采用三角隶属度函数来定义输入、输出变量，并取每个输入输出变量有5 个模糊子集，对其定义为负大(NB)，负小(NS)，零(Z0)，正小(PS)，正大(PB)。同时根据隶属度函数与仿真观察，可分别确定各模糊控制器输入输出变量的论域和量化因子如表1 所示。根据仿真验证采用的模糊控制规则如表2 ～3 所示。

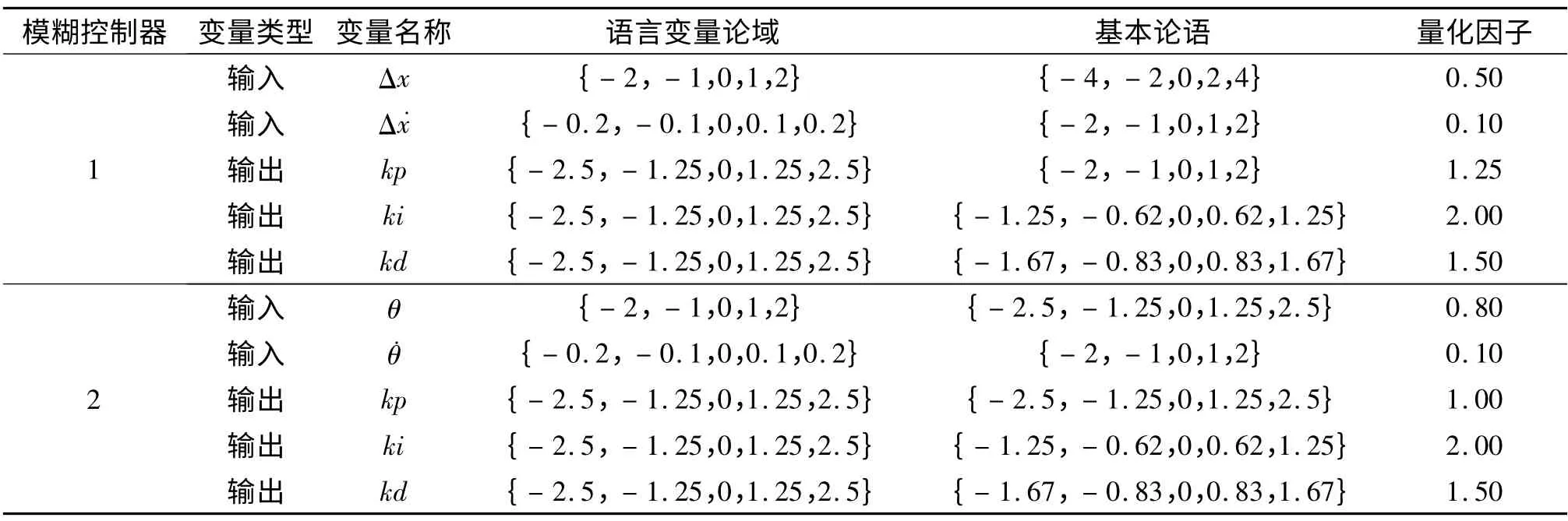
表1 各模糊控制器输入输出变量的论域和量化因子Tab.1 Domain and quantitative factors of kinds of fuzzy controller input and output variables

表2 位置模糊规则Tab.2 Table of position fuzzy rules

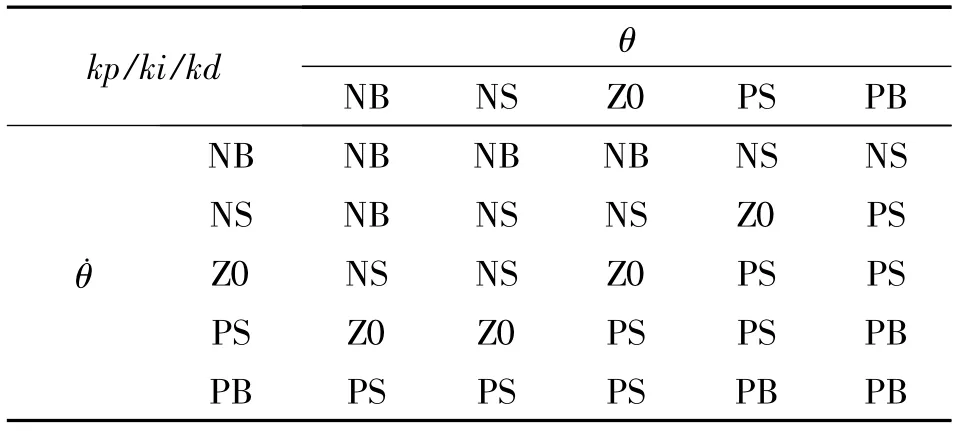
表3 摆角模糊规则Tab.3 Table of pendulum angle fuzzy rules

3 仿真实验

文中取小车的质量M = 2 kg，摆杆质量m =0.1 kg，倒摆长度l = 0.5 m，摆杆转动惯量为I =0.02 kg·m2，小车的摩擦系数为b =5 kg/s;并设定该系统中小车的初始位置为0.5 m，摆杆的初始摆角为0.1 rad。对上述倒立摆控制系统进行仿真，其仿真实验结果如图3，4 所示。其中，图3 为分类解耦下的模糊PID 控制仿真结果，图4 为分类解耦下的常规PID 控制仿真结果。

图3 模糊PID 控制仿真结果Fig.3 Fuzzy PID control simulation results

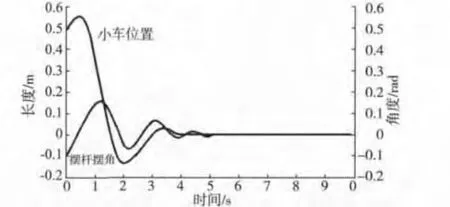
图4 常规PID 控制仿真结果Fig.4 Conventional PID control simulation results

由此可以看出，使用模糊PID 控制方案不但使系统达到了所要求的性能指标，而且用该控制策略的性能明显优于仅仅采用常规PID 控制的性能品质，它有效地缩小了系统的超调量，缩短了稳定时间，减少了系统的输出振荡，同时也提高了系统的鲁棒性能。

4 结 语

针对倒立摆系统是一个多变量、非线性、强耦合不稳定的高阶系统，通过对倒立摆系统数学模型分析，采用了一种分类解耦的线性化方法，对分类偶的变量分别进行模糊PID 控制，然后使两种控制器在不同范围内发挥其各自优势，即在误差和误差变化率都不大的情况下，发挥PID 控制精度高、稳态特性好的优势，在误差和误差变化率较大的情况下发挥模糊控制器的抗干扰能力强和快速性的优势。仿真结果表明，这种控制器不但降低了PID 参数整定的难度，提高了系统的动态性能与稳态性能，而且提高了系统的鲁棒性。

［1］宋君烈，肖军，徐心和.倒立摆系统的Lagrange 方程建模与模糊控制［J］.东北大学学报:自然科版，2002，23(4):333－337.

SONG Junlie，XIAO Jun，XU Xinhe.Modeling and control method of the inverted pendulum system［J］.Journal of Northeastern University:Natural Science，2002，23(4):333－337.(in Chinese)

［2］郭钊侠，方建安，苗清影.倒立摆系统及其智能控制研究［J］.东华大学学报:自然科学版，2003，29(2):122－126.

GUO Zhaoxia，FANG Jianan，MIAO Qingying. Inverted pendulum and the research of intelligent control［J］. Journal of Northeastern University:Natural Science，2003，29(2):122－126.(in Chinese)

［3］侯涛，牛宏侠.倒立摆的双闭环解耦切换模糊控制设计与仿真［J］.兰州交通大学学报:自然科学版，2007，26(1):29－31.

HOU Tao，NIU Hongxia.Design and simulation of double closed－loop decoupling switch fuzzy control on inverted pendulum［J］.Journal of Lanzhou Jiaotong University:Natural Sciences，2007，26(1):29－31.(in Chinese)

［4］马志涛，侯涛，张红兵，等.倒立摆系统的T－S 模糊控制研究［J］.微计算机信息，2006，22(28):69－71.

MA Zhitao，HOU Tao，ZHANG Hongbing，et al. Study of T－S fuzzy control in inverted pendulum system［J］. Microcomputer Information，2006，22(28):69－71.(in Chinese)

［5］齐峰，万少松.对倒立摆控制系统设计的仿真与比较［J］.空军工程大学学报，2007，8(2):29－32.

QI Feng，WAN Shaosong.The comparison and simulation of control idea for a inverted pendulum system［J］.Journal of Air Force Engineering University:Natural Science Edition，2007，8(2):29－32.(in Chinese)

［6］湛力，孙鹏，陈雯柏.倒立摆系统的自摆起和稳定控制［J］.计算机仿真，2006，23(8):289－292.

ZHAN Li，SUN Peng，CHEN Wenbai. Control of swing up and stabilization of an inverted pendulum system［J］Computer Simulation，2006，23(8):289－292.(in Chinese)

［7］韩东方.一级直线型倒立摆的控制及实现［J］.汕头大学学报:自然科学版，2007，22(2):28－37.

HAN Dongfang.Control and implementation of the single linear inverted－pendulum［J］. Journal of Shantou University:Natural Science，2007，22(2):28－37.(in Chinese)

［8］蔡增威，刘德春，张晓华.种基于鲁棒性设计的一阶倒立摆双闭环控制方法［J］.控制理论与应用，2004，23(4):10－15.

CAI Zengwei，LIU Dechun，ZHANG Xiaohua.A robust double－loop control to single inverted pendulum［J］.Control Theory and Applications，2004，23(4):10－15.(in Chinese)

［9］曹晓燕，于立萍，姚文韬.基于粒子群算法的模糊控制在倒立摆中的应用［J］.计算机技术与发展，2008，18(6):151－155.

CAO Xiaoyan，YU Liping，YAO Wentao. Particle swarm optimization in fuzzy control of an inverted pendulum［J］. Computer Technology and Development，2008，18(6):151－155.(in Chinese)