QPSO 算法实现图像边缘检测

费赓柢， 李岳阳， 孙 俊

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡214122)

边缘检测算法通过检测包含不同区域的边缘来解决图像分割问题。边缘由边缘像素构成，而边缘像素是图像中灰度突变的那些像素［1］。Robert 算子、Prewitt 算子、Sobel 算子都是基于梯度的算子［2-3］，它们使用不同的模板来求图像中各像素点处一阶偏导数的近似值。这些基于梯度的边缘检测算法易于实现，但它们不仅对边缘信息敏感，对噪声同样也很敏感［4］。为了减少噪声对图像的影响，通常在求导之前先对图像进行滤波。常用的滤波器主要是高斯函数的一阶和二阶导数。J.Canny 采用高斯函数的一阶导数，推导出了最佳边缘检测算子——Canny 算子［5］。而计算机视觉的创始人Marr D［6］提出采用Laplacian 算子求高斯函数的二阶导数得到Laplacian of Gaussian(LOG)滤波算子。在传统算法的基础上，学者提出一些改进的算法［7-9］。这些经典的算法能在一定程度上有效地提取出图像中的边缘，但在算法中需确定一些参数的值，而这些参数的最优值的确定，是一个比较困难的问题。此外，当图像中的噪声变大时，上述算法的边缘检测能力急剧下降。而数字图像在其获取、传输过程中因种种原因可能导致在正常的图像数据中混入噪声信号［10］。因此许多边缘检测器在检测前，需先进行滤波操作，这样就增大了系统的复杂性。

在噪声图像中，细节或边缘与噪声之间的区别并不明显。这种信息的不确定性和不完整性给数字图像处理带来了困难，而模糊理论正好能适应这些不确定性。人工神经网络方法能够根据学习样本找出输入与输出数据之间的内在联系，特别适合图像处理中许多非线性问题。近年来，神经模糊(NF)理论综合了模糊理论模拟图像处理过程中的不确定性的能力和人工神经网络强大的学习能力，逐渐应用在图像处理过程中［11-15］。其中M.Emin，Yüksel［13］提出了一个神经模糊系统图像边缘检测算法，该算法的其中一个特点是:在对噪声图像进行边缘检测前，无需进行噪声滤波过程。

对于被椒盐脉冲噪声污染的灰度图像，我们提出一个基于QPSO 的图像边缘检测算法。在提出的新算法中，将4 个自适应神经模糊推理系统(ANFIS)子检测器和一个后处理块组成一个图像边缘检测器。每个ANFIS 子检测器都是一个4 输入单输出的一阶Sugeno 模糊推理系统［16］。在构造ANFIS 时，采用何种方法优化确定其内部参数是设计ANFIS 系统的一个重要环节。许多ANFIS 的参数优化是基于梯度(Gradient Descent，GD)的［13-15］，而基于梯度的优化方法，其结果依赖于参数初始化值，要找到全局最优化参数比较困难。孙俊等［17-18］在粒子群算法(Particle Swarm Optimization，PSO)［19］基础上，提出了基于量子行为粒子群优化(Quantum-behaved Particle Swarm Optimization，QPSO)算法，对标准测试函数测试结果表明，QPSO算法的全局搜索性能相比PSO 算法有了很大的改进。

文中所提出的边缘检测算法分两步进行，首先每个ANFIS 子检测器需单独进行训练，采用QPSO优化系统中的前提参数，结论参数由线性最小二乘法(LSE)得到。4 个ANFIS 子检测器训练完成后，可以和一个后处理块一起构成一个边缘检测器，对测试图像进行边缘检测。在仿真实验中，采用Malik 数据库中的二幅图像，将所提算法与其它4 种算法相比较，测试其边缘检测性能。定性和定量评价的结果证明了所提算法与其它算法相比具有更强的边缘检测能力。

1 算 法

1.1 边缘检测器

图1 是提出的图像边缘检测器结构图。该检测器包含4 个ANFIS 子检测器和1 个后处理块。每个ANFIS 子检测器都是1 个4 输入单输出的一阶Sugeno 模糊推理系统，其4 个输入由相应的数据提取块提供。4 个数据提取块分别对应图2 中水平、垂直、左对角线和右对角线4 个方向上不同的拓扑结构。数据提取方法:以当前操作像素为中心，得到一个3 ×3 窗口，依照水平、垂直、左对角线和右对角线4 种不同的拓扑结构得到像素灰度值p1，p2，p3和中值m，令每个ANFIS 的4 个输入x1，x2，x3，x4分别为

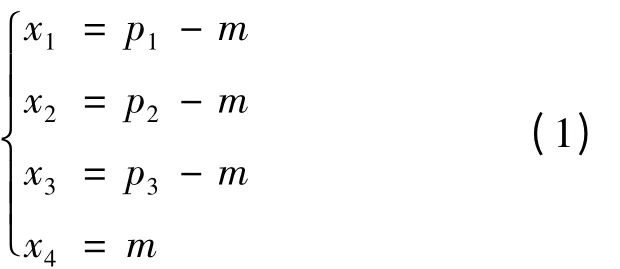
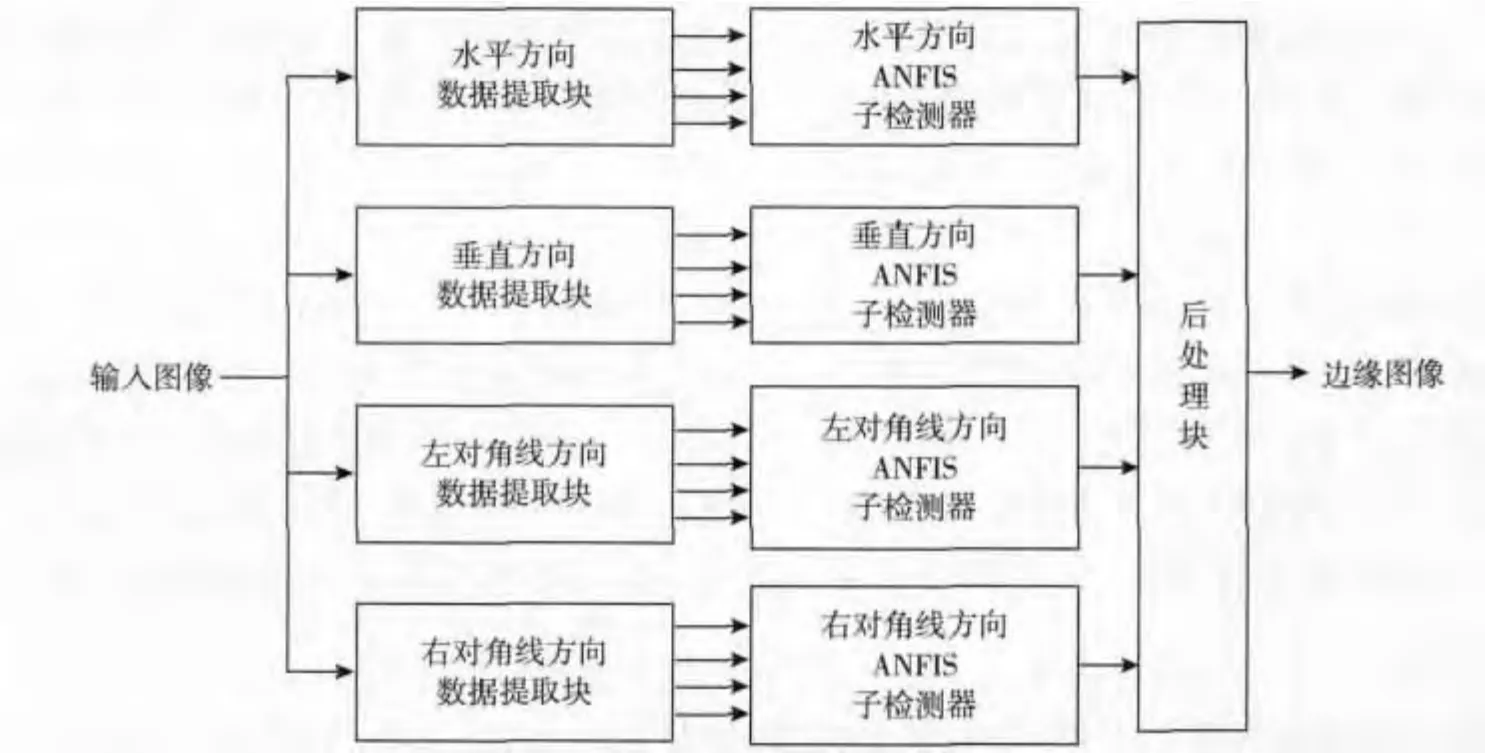
图1 边缘检测器结构Fig.1 Structure of the proposed edge detector

图2 4 个数据提取块对应的拓扑结构Fig.2 Four pixel neighborhood topologies

1.2 ANFIS 子检测器

图1 中4 个ANFIS 子检测器的内部结构都相同，都是1 个4 输入单输出的一阶Sugeno 模糊推理系统。对于输入图像中的当前操作像素，根据1.1 节所述的数据提取方法，每个数据提取块为相应的ANFIS 子检测器提供4 个输入x1，x2，x3，x4。对于每个输入，分别定义3 个广义钟型隶属函数，则每个ANFIS 包含81(即34)条规则，其模糊规则集如下:

规则1:if (x1is M11)and (x2is M21)and (x3is M31)and (x4is M41)，then y1= d11x1+ d12x2+d13x3+d14x4+ d15;

规则2:if (x1is M11)and (x2is M21)and (x3is M31)and (x4is M42)，then y2= d21x1+ d22x2+d23x3+d24x4+ d25;

规则3:if (x1is M11)and (x2is M21)and (x3is M31)and (x4is M43)，then y3= d31x1+ d32x2+d33x3+d34x4+ d35;

┆

规则81:if (x1is M13)and (x2is M23)and (x3is M33)and (x4is M43)，then y81= d81，1x1+d81，2x2+d81，3x3+ d81，4x4+ d81，5

其中Mij表示第i 个输入的第j 个隶属函数，dkl为结论参数，yk为系统根据第k 个规则得到的输出，i = 1，2，3，4，j = 1，2，3，k = 1，…，81，l = 1，…，5。对于输入xi，定义的广义钟型隶属函数为

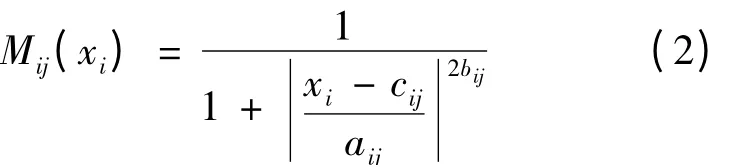
其中aij，bij，cij为前提参数。

ANFIS 的输出Y 等于各规则输出yk的加权平均:

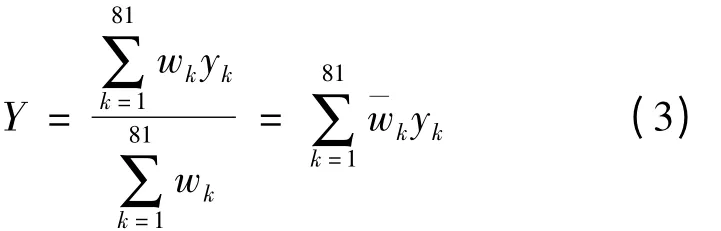
式中加权系数wk表示第k 条规则的激励强度，¯wk为wk的规一化值。wk的计算公式如下:

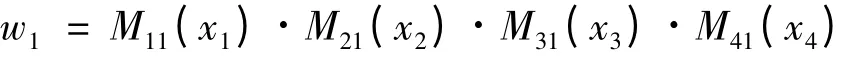
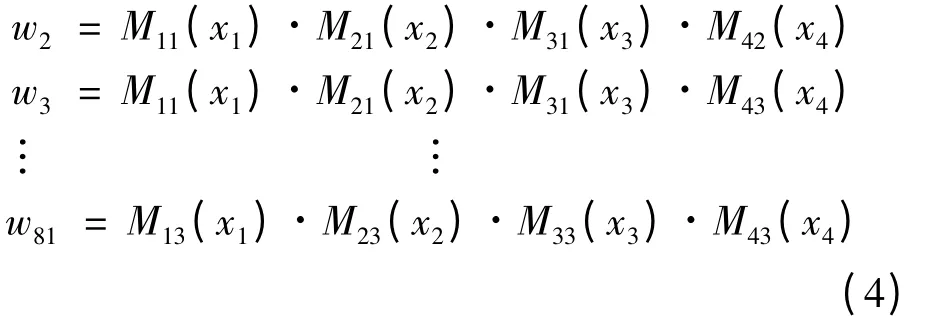
1.3 后处理块

图1 中，由4 个ANFIS 子检测器可分别得到4 个输出，记为YK(K = 1，2，3，4)。这4 个输出即为后处理块的输入。后处理块按式(5)对这4 个输入取平均值，记为Yav。再按式(6)将Yav与一个阈值Th 相比较，求得检测器的最终输出YF。需要说明的是，文中所有图像的像素灰度值都定义在区间［0，1］之间。最终输出YF的值为0 表示当前操作像素是边缘像素，显示为黑色;YF的值为1 表示当前操作像素不是边缘像素，显示为白色。

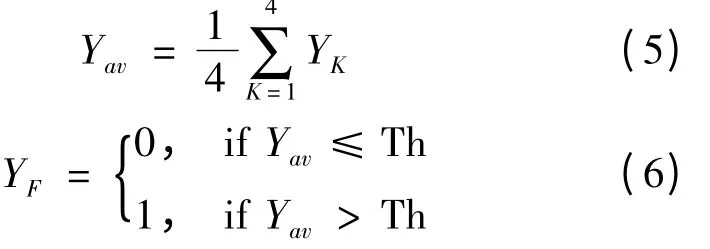
一个像素是否检测为边缘由式(6)中的阈值Th 决定。当Th 值接近0 时，检测为边缘的像素会变少，也就是说，一些边缘像素可能会误检为非边缘像素。相反，当Th 值接近1 时，检测为边缘的像素会变多，但一些非边缘像素可能会误检为边缘像素。在后面仿真实验中，将对Th 值进行分析确定。

1.4 混合学习算法

对于ANFIS 中参数的优化，Jang 在文献［16］中提出了混合学习算法，即前提参数通过梯度法进行优化，结论参数用线性最小二乘法(LSE)得到。由于QPSO 算法具有很好的全局搜索性能，文中采用QPSO 算法对前提参数进行优化，结论参数仍用LSE得到。下面简述PSO 算法、QPSO 算法和LSE 算法。

1.4.1 PSO 算法 1995 年由美国社会心理学家Kennedy 和电气工程师Eberhart 提出的PSO 算法［19］，主要思想来源于对鸟类群体行为的研究。在PSO 算法中，每一个优化问题的解可以看做是搜索空间的一只鸟，称为“粒子”，每个粒子由目标函数确定其适应值，每个粒子以一定的速度在解空间中运动，粒子通过追随自身的个体最好位置与群体的全局最好位置来动态地调整自己的位置信息。

假设一个群体有M 个粒子飞行在D 维空间。对于第i 个粒子，其位置和速度分别为:xi= (xi1，xi2，…，xid，…，xiD)，vi= (vi1，vi2，…，vid，…，viD)，其中i =1，2，…，M，d = 1，2，…，D。每个粒子的位置矢量即为ANFIS 系统中的一组前提参数，通过PSO 算法对每个粒子的位置进行优化更新，最终确定一个最优的粒子，其位置矢量即为所要求的前提参数。第i 个粒子具有最好目标函数值的位置称为个体最好位置(pbest)，表示为Pi= (Pi1，Pi2，…，PiD)。整个粒子群具有最好目标函数值的位置称为全局最好位置(gbest)，表示为:G = (G1，G2，…，GD)。

在第(n +1)次迭代，第i 个粒子的速度和位置的更新公式可描述如下:

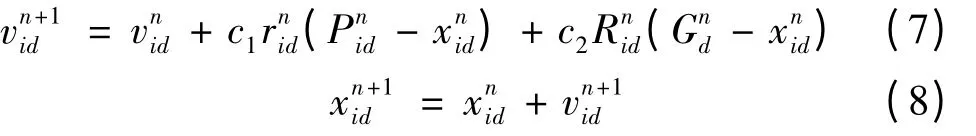
其中，c1和c2称为学习因子和是(0，1)间均匀分布的相互独立的随机数序列。

考虑最小化问题，第i 个粒子个体最好位置更新公式为

其中，f 是目标函数。整个粒子群的全局最好位置Gn+1=，其中

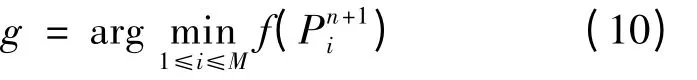
1.4.2 QPSO 算法 Van den Bergh［20］已经证明了PSO 算法不能收敛于全局最优解。孙俊等研究者发现，人类学习过程与粒子的量子行为极为相似，具有很大的不确定性。所以每个个体都可以用量子空间中的一个粒子来描述，并根据群体智能的聚集性，建立量子的δ 势阱模型，设计了新的群体智能算法——QPSO 算法［17-18］。

Clerc M［21］的研究表明，粒子i 的收敛过程以点

一般情况下，学习因子c1和c2相等，则式(11)可改写为

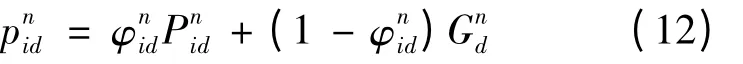
通过采用蒙特卡罗随机模拟的方式，粒子的位置更新方程可写为

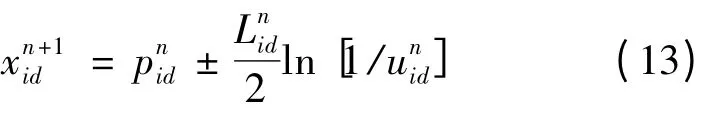
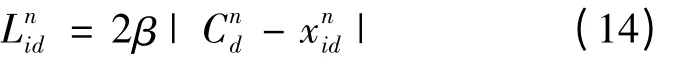
其中β 称为收缩－扩张系数。一般情况下，参数β 可采用随迭代次数线性减小的方式控制。Cn= (，，…，)称为平均最好位置(mbest)，定义为所有粒子个体最好位置的平均，即

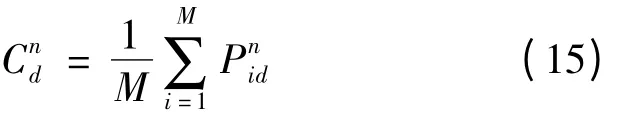
这样，式(13)的粒子位置更新公式可变为

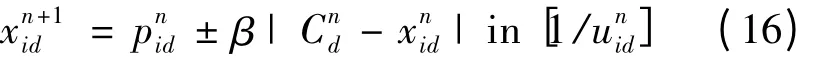
式中取“+”或取“－”的概率都为0.5。最终，式(12)，(16)就构成了QPSO 算法中每个粒子的位置更新公式。

1.4.3 LSE 算法 每次迭代时，当粒子的位置(即前提参数)更新后，采用LSE 算法可确定相应的结论参数。假设有N 组训练数据，对于输入(，，，)T，t = 1，2，…，N，式(3)可改写为

其中

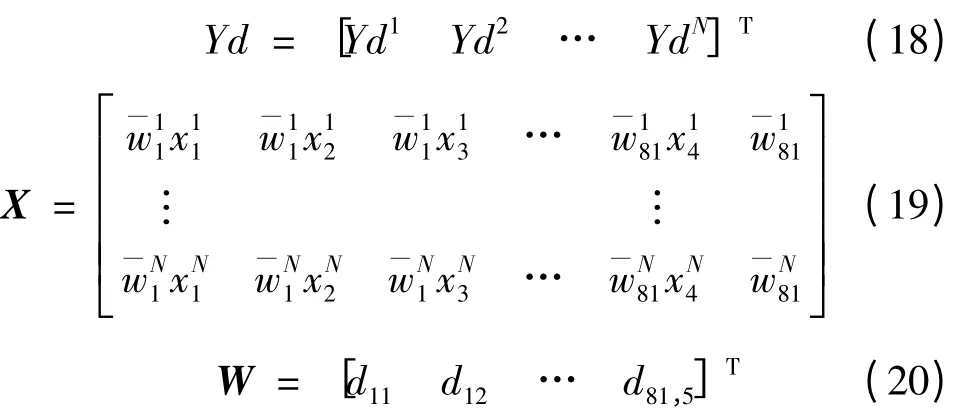
其中T 为转置符号，Ydt是第t 组输入对应的期望输出。由结论参数组成的矩阵W 可由式(17)采用LSE算法得到［22］。

1.5 ANFIS 子检测器的训练过程

在使用图1 所示边缘检测器对测试图像进行边缘检测前，每个ANFIS 子检测器都需单独进行训练。图3 是单个ANFIS 子检测器训练优化过程图。训练图像可通过计算机人工构造得到，每个ANFIS 子检测器都采用相同的训练图像。图4(a)是每个ANFIS 子检测器的原始训练图像，该图像大小为128 ×128，是由1 024 个4 ×4 色块组成，每个色块中的16 个像素具有相同的灰度值，不同色块的灰度值各不相同，遍取0 到255 中的所有值，不同灰度值的色块在图像中的位置是随机的。图4(b)是子检测器输入的训练图像，是在图4(a)原始图像上添加30% 的椒盐脉冲噪声得到的噪声图像。图4(c)是根据图4(a)原始图像得到的边缘标志图像，也就是子检测器期望输出的训练图像，图中像素灰度值为0，表示当前像素是边缘像素，显示为黑色，像素灰度值为1，表示当前像素不是边缘像素，显示为白色。

图3 ANFIS 子检测器训练优化过程Fig.3 Training process for an ANFIS sub-detector

文中采用计算机人工构造的图像训练后的边缘检测器，对于测试图像的边缘检测具有鲁棒性。在仿真实验中，为测试文中所提出算法的边缘检测效果，分别对图5(a)中2 幅从Malik 数据库［23-24］中得到的图像进行测试。采用计算机人工构造的图像训练后的边缘检测器，对于测试图像的边缘检测具有鲁棒性，其两方面含义为:一是测试图像与训练图像可完全不同;二是训练图像中的噪声密度也无需与测试图像中的噪声密度相同，测试图像也可以是原始图像(非噪声图像)，训练后的边缘检测器对受不同噪声密度污染的各类测试图像边缘检测效果均较好。

图4 人工训练结果Fig.4 Artificial training images

每个ANFIS 子检测器均需要单独进行训练，采用基于QPSO 和LSE 的混合学习算法确定ANFIS 中前提参数和结论参数。QPSO 算法中的每个粒子的位置就是一组前提参数序列，按1.4 节所述优化方法得到具有最好目标函数值的粒子，其位置即为所求的前提参数，由该前提参数采用LSE 算法得到所对应的结论参数。

假设由图4(b)输入的训练图像和图4(c)期望输出的训练图像得到所有的训练数据N 组。对于每一组输入()T，t = 1，2，…，N，ANFIS 子检测器的实际输出和期望输出分别为Yt和Ydt。目标函数可由平均均方根误差(RMSE)表示:

ANFIS 子检测器的训练过程可描述如下:

1)设迭代次数n = 0。初始化粒子群，包括粒子的个数M，搜索空间D(ANFIS 系统中前提参数的个数)，随机初始化每个粒子初始位置。

3)由式(15)得到所有粒子个体的平均最好位置。选择一个合适的β 值，由式(12)，(16)对每个粒子的位置进行更新，采用LSE 算法得到相应的结论参数，由式(21)得到每个粒子的目标函数值，再由式(9)更新个体最好位置。最后，比较所有粒子的个体最好位置，根据式(10)得到全局最好位置Gn+1。同时保存具有全局最好位置粒子所对应的结论参数矩阵W。

4)当达到迭代结束条件时，训练结束，全局最好位置Gn+1即为所要确定的前提参数，保存的矩阵W 即为要确定的结论参数。当迭代结束条件未达到时，设n = n +1，转到步骤3)。

1.6 边缘检测过程

如图1 所示，当4 个ANFIS 子检测器都训练完毕，就可以和一个后处理块一起构成一个边缘检测器，对测试图像进行边缘检测。检测过程可描述如下:

1)以测试图像为输入图像，对其中所有像素，按从上到下，从左到右的顺序，逐个进行操作;

2)对当前操作像素，4 个数据提取块分别按1.1 节中所述方式得到相应子检测器的4 个输入;

3)每个ANFIS 子检测器都会得到一个输出，这4 个输出即为后处理块的4 个输入，后处理块按1.3节中所述方式对这4 个输入进行相应处理，得到一最终输出，该输出即为输入图像当前操作像素的边缘标志值;

4)选取输入图像中下一个像素作为当前操作像素，重复步骤2)至4);

5)当输入图像中所有像素经过检测器都得到输出后，就能得到该输入图像相对应的边缘图像。

2 实验结果

为测试算法检测边缘的性能，可将各算法得到的边缘图像与基准边缘图像(Ground Truth，GT)相比较。文中2 幅从Malik 数据库［23-24］中得到的图像可用来测试各种算法的边缘检测能力。该数据库中包含了500 幅自然图像和相应的由人工得到的基准边缘图像。图5(a)和图5(b)分别显示2 幅原始图像和其对应的基准边缘图像，其大小为481 × 321。为测试边缘检测器在噪声存在情况下的检测能力，在2 幅原始图像中分别添加3% ～30% 椒盐脉冲噪声。原始图像和噪声图像都作为测试图像，用于测试各种算法的边缘检测性能。

图5 测试结果Fig.5 Testing images

文 中 对 所 提 算 法 与Sobel 算 子［2-3］、LOG 算子［6］，Canny 算子［5］和文献［13］中的算法分别进行比较，给出定性和定量评价，具体测试指标包括:边缘检测的准确性和对噪声的鲁棒性。对于文献［13］中算法，在仿真实验中，采用了4 个子检测器，每个子检测器中的参数使用Levenberg-Marquardt 算法进行优化。对于文中所提算法，采用4 个ANFIS 子检测器，每个子检测器中的参数使用QPSO 和LSE 混合学习算法确定。每个子检测器有4 个输入，每个输入对应3 个广义钟型隶属函数，每个隶属函数有3个参数(aij，bij，cij)，因此每个子检测器有4 × 3 ×3 =36 个前提参数。QPSO 算法中每个粒子的维数D与前提参数的个数相等，也就是36。文中仿真实验中，考虑到优化的效果和运行效率，粒子群的大小M设为30。收缩-扩张系统β 随迭代次数线性减小，其取值范围为［1，0.5］。1.3 节式(6)中的阈值Th 对边缘检测效果的影响如图6 所示。正如1.3 节中所描述的，当Th 值小时，检测为边缘的像素会少，一些边缘像素没有被检测出来，如图6(a)所示;当Th 值大时，检测为边缘的像素会多，一些非边缘像素会误检为边缘像素，如图6(d)所示。文中Th 值设为0.38。

图6 使用不同阈值得到的边缘结果Fig.6 Edge maps for different threshold

2.1 定性评价

图7 显示的是对图5(a)中原始图像进行边缘检测的结果。图7(a)为原始图像，图7(b)～(f)分别为用Sobel 算子、LOG 算子、Canny 算子、文献［13］算法和文中算法检测所得的边缘图像。从图中可以看出，LOG 和Canny 算子会检测出过多的边缘，而Sobel 算子检测出的边缘会少，一些边缘会丢失。文献［13］算法和文中算法得到的边缘检测图像相对较好。

图7 使用不同算法得到的边缘检测结果Fig.7 Edge detecting performance using different detectors

为测试各算法在噪声存在情况下边缘检测的能力，在仿真实验中，将噪声图像也作为测试图像。图8 显示的是对含噪10% 的测试图像进行边缘检测的结果。图8(a)为含10% 的椒盐脉冲噪声测试图像，图8(b)～(f)分别为用Sobel 算子、LOG 算子、Canny 算子、文献［13］算法和文中算法检测所得的边缘图像。从图中可以看出，Sobel 算子、LOG算子和Canny 算子在噪声存在的情况下，边缘检测的能力急剧下降，许多噪声被误检为边缘。而噪声对文献［13］算法和文中算法影响较小，这两种算法仍能够较正确地检测出边缘，对噪声具有鲁棒性。相比较文献［13］算法的边缘检测结果，文中算法在正确检测边缘和对噪声的鲁棒性方面效果更佳。

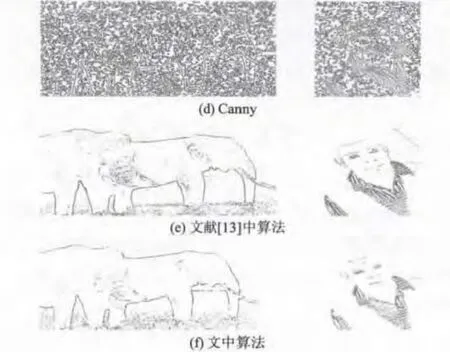
图8 使用不同算法得到的边缘检测结果Fig.8 Edge detecting performance using different detectors

2.2 定量评价

在文中仿真实验中，还采用了定量评价标准TP、TN、Score［25］、PSNR(峰值信噪比)［26］，来评价各算法的边缘检测性能。

其中True Positive(TP)表示同时被基准边缘图像(GT)和检测器得到的边缘图像认定为边缘像素的个数;True Negative(TN)表示同时被基准边缘图像(GT)和检测器得到的边缘图像认定为非边缘像素的个数。由评价标准Score 的定义可知，其大小反映了检测器正确检测边缘的能力，Score 值越大，表明正确检测边缘的能力越强。

图9 显示的是使用不同的检测算法得到Score值，检测图像包括原始图像和含3% ～30% 脉冲噪声图像。图9 中对应于每个噪声密度的Score 值是2幅图像Score 值的平均值。从图中可以明显看出，相比较其它算法，文中算法的Score 值为最大，这表明文中算法的正确检测边缘的能力最强。

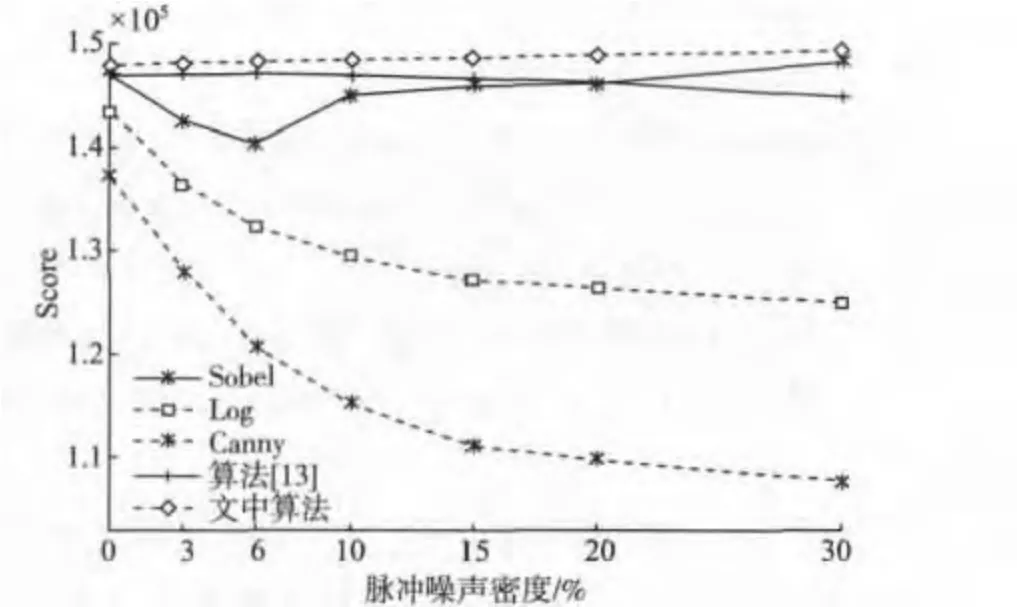
图9 使用不同算法得到的Score 值Fig.9 Score value for all detectors

为评价检测器对噪声的鲁棒性，可以用PSNR指标，即对于某个检测器，将由噪声图像得到的边缘图像和由原始图像(非噪声图像)得到的边缘图像相比较。PSNR 可定义为

其中O(i，j)和N(i，j)分别表示由原始图像得到的边缘图像像素和由噪声图像得到的边缘图像像素，图像大小为M ×N。PSNR 值越大表示检测器对噪声的鲁棒性越好。

图10 显示的是使用不同算法得到的PSNR 值。从图中可以看出，文献［13］算法和文中算法得到的PSNR 值要远远大于3 个传统算法(Sobel 算子、LOG算子、Canny 算子)得到的PSNR 值，这进一步证明了2.1 节定性评价得到的结论，即在噪声存在的情况下，这3 种传统算法的边缘检测能力较差，而噪声对文献［13］算法和文中算法的影响相对较小，且文中算法对噪声的鲁棒性最佳。

3 结 语

文中提出了一个基于QPSO 算法的图像边缘检测器，该检测器包含4 个ANFIS 子检测器和一个后处理块。仿真实验证明，相比较其它4 种算法，文中所提出的算法具有更强的边缘检测能力，具体表现在正确检测边缘性能和对噪声的鲁棒性两方面。

图10 使用不同算法得到的PSNR 值Fig.10 Average PSNR value for all detectors

文中所提出的新算法特色在于，在对噪声图像进行边缘检测前，不需要先进行滤波预处理过程。训练图像可由计算机人工构造，并由仿真实验可知，采用这样的方法构造的图像训练后的检测器，对于噪声图像边缘检测具有鲁棒性，即测试图像与训练图像可完全不同，训练图像中的噪声密度也无需与测试图像中的噪声密度相同。QPSO 优化算法可用于ANFIS 的参数优化中，较大地提高了新算法的边缘检测性能。

［1］Gonzalez R C，Woods R E.数字图像处理［M］.2 版.阮秋琦，译.北京:电子工业出版社，2003.

［2］章毓晋.图像分割［M］.北京:科学出版社，2001.

［3］章毓晋.图像处理和分析基础［M］.北京:高等教育出版社，2002.

［4］田捷.实用图像处理技术［M］.北京:电子工业出版社，1994.

［5］Canny J.A computational approach to edge detection［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1986，PAMI-8(6):679-698.

［6］Marr D.视觉计算理论［M］.姚国正，译.北京:科学出版社，1988.

［7］周凌翔，顾伟康.最佳边缘检测的准则与算子［J］.模式识别与人工智能，1998(1):54-61.

ZHOU Lingxiang，GU Weikang. The best criterion and operator of edge detection［J］. Pattern Recognition and Artificial Intelligence，1998(1):54-61.(in Chinese)

［8］王植，贺赛先.一种基于Canny 理论的自适应边缘检测方法［J］.中国图象图形学报，2004(8):65-70.WANG Zhi，HE Saixian.An adaptive edge-detection method based on Canny algorithm［J］.Journal of Image and Graphics，2004(8):65-70.(in Chinese)

［9］陆宗骐，梁诚.用Sobel 算子细化边缘［J］.中国图象图形学报，2000(6):71-75.LU Zongqi，LIANG Cheng. Edge thinning based on Sobel operator［J］. Journal of Image and Graphics，2000(6):71-75. (in Chinese)

［10］霍宏涛.数字图像处理［M］.北京:北京理工大学出版社，2002.

［11］LI Y，CHUNG F L，WANG S.A robust neuro-fuzzy network approach to impulse noise filtering for color images［J］.Applied Soft Computing，2008，8(2):872-884.

［12］LI Y，LUO H，SUN J.A New Impulse Noise Filtering Algorithm Based on a Neuro-Fuzzy Network，in Combinations of Intelligent Methods and Applications［M］.Hatzilygeroudis I，Palade V:Springer Berlin Heidelberg，2013:41-56.

［13］Emin M，Yüksel. Edge detection in noisy images by neuro-fuzzy processing［J］. AEU-International Journal of Electronics and Communications，2007，61(2):82-89.

［14］Suryakant Dhir R. Novel adaptive neuro-fuzzy based edge detection technique［J］. International Journal of Computer Applications，2012，49(4):23-27.

［15］Bhardwaj K，Mann P S.Adaptive neuro-fuzzy inference system (ANFIS)based edge detection technique［J］.International Journal for Science and Emerging Technologies with Latest Trends，2013，8(1):7-13.

［16］JANG J S R，SUN C T.Neuro-Fuzzy and Soft Computing:a Computational Approach to Learning and Machine Intelligence［M］.Upper Saddle River，NJ，USA:Prentice-Hall Inc，1997.

［17］Jun S，Bin F，Wenbo X. Particle swarm optimization with particles having quantum behavior［C］//Proceedings of Congress on Evolutionary Computation.［s.l.］:IEEE Press，2004，11:325-331.

［18］Jun S，Wenbo X，Bin F.A global search strategy of quantum-behaved particle swarm optimization［C］//Proceedings of Conference on Cybernetics and Intelligent Systems.［s.l.］:IEEE Press，2004，11:111-116.

［19］Kennedy J，Eberhart R. Particle swarm optimization［C］//Proceedings of 1995 IEEE International Conference on Neural Networks.［s.l.］:IEEE Press，1995，4:1942-1948.

［20］Bergh F V D. An analysis of particle swarm optimizers［EB/OL］.［2001-05-13］(2014-11-15). Parsproje. com/tarjome/computer/cm11.pdf

［21］Clerc M，Kennedy J. The particle swarm-explosion，stability，and convergence in a multidimensional complex space［J］. IEEE Transactions on Evolutionary Computatio，2002，6(1):58-73.

［22］Hines J W.Fuzzy and Neural Approaches in Engineering，MATLAB Supplement［C］//Haykin S.Adaptive and Learning Systems for Signal Processing，Communications and Control Series.New York，NY:John Wiley and Sons，1997.

［23］Anon.Berkeley segmentation and boundary detection benchmark and dataset［EB/OL］.［2003-06-20］(2014-10-06). http://www.eecs.berkeley.edu/Research/Project/CS/vision/grouping/segbench

［24］Martin D，Fowlkes C，Tal D，et al.A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics［C］//Proceedings of the Eighth IEEE International Conference on Computer Vision.［s.l.］:IEEE Press，2001，2:416-423.

［25］Etemad S A，White T.An ant-inspired algorithm for detection of image edge features［J］.Applied Soft Computing，2011，11(8):4883-4893.

［26］ZHU S Y，Plataniotis K N，Venetsanopoulos A N.Comprehensive analysis of edge detection in color image processing［J］.Optical Engineering，1999，38(4):612-625.