基于人工蜂群算法的食品供应链召回优化

陆 欣， 沈艳霞 ， 张君继

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡214122)

近年来，各类由于原料问题导致的食品质量安全事故频发，引起了食品质量监管部门、加工企业与消费者的重视［1］。消费者迫切要求监管部门建立起食品供应链的全程追溯系统，在食品质量出现问题后，企业能够及时追踪到发生质量问题的源头并召回相关批次，将危害降到最低［2］。从农场到餐桌的食品供应链包括原料的供应、食品的加工、物流、餐饮等环节［3］。其中最为重要的是加工环节，加工流程与加工工艺直接改变了食品的性状，也增加了追溯的难度。因此，实现食品加工环节的召回优化，对食品的供应链全程追溯有重要意义。

将电子和通信技术应用到食品追溯领域，如二维码和RFID 技术，能够准确有效地溯源并在发生食品质量危机时实现召回，但这些技术无助于减小召回规模。在发生食品质量安全事故时，企业必须对存在潜在质量问题的全部批次产品召回和销毁，这影响了企业对于建立供应链追溯的积极性［4］。只有兼顾消费者和食品加工企业的利益，在食品加工环节对原材料批次分散进行优化，降低召回规模，减小损失，提高召回效率，监管部门才能建立起有效的食品供应链全程追溯系统［5］。

针对食品供应链加工环节的召回优化问题，国内外学者展开了相关研究。Dorp 等［6］采用高津托图(Gozinto graphs)描 述 追 溯 模 型;Dupuy 等［7］在Dorp 基础上，根据法国香肠加工业的实际情况提出批次分散(Batch dispersion)模型，并给出该模型的混合整数线性规划 (Mixed-Integer Linear Programming，MILP)，同时采用LINGO 进行优化求解;Dabbene 等［8］基于批次分散模型，提出最坏召回代价和平均召回代价，同时采用3 层模型对评估指标进行优化;Lobna 等［9］给出了模型形式化描述，并分析算法强度，指出该模型为NP 难度问题，提出启发式算法进行求解;Tamayo 等［10］提出用遗传算法优化该追溯模型，但仅适用于小规模的召回模型;李锋等［11］通过分段门限粒子替换策略的改进粒子群算法进行优化，取得了较为满意的效果。但改进粒子群算法所需选择门限参数多达7 个，在实际复杂生产环节中，很难保证参数设置的合理性，实际应用效果有限。

Karaboga 等［12］于2005 年提出了人工蜂群算法(Artificial Bee Colony，ABC)，它是一种基于蜜蜂采蜜行为的群智能优化算法。该算法的主要特点是设置参数少、收敛速度快、求优精确度高，通过人工蜂群个体的局部寻优，从而在群体中凸显全局最优值。该算法提出之后，已被用于求解旅行商问题、车辆路径问题、车间调度问题，都取得了较好的求解效果，有效地解决了高维、多极值、多约束等工程问题［13-14］。

因此，文中提出将人工蜂群算法应用到食品供应链追溯系统召回优化问题。首先对食品加工环节进行分析，给出食品召回的批次分散模型;然后针对多层批次分散模型巨大，难以求解的问题，引入人工蜂群算法进行优化求解，提高优化性能。

1 食品加工环节批次分散模型

食品供应链全程追溯系统，可对加工环节进行批次分散优化，在发生食品安全事件后能有效减少召回批次［15］。食品加工环节批次分散模型及追溯示意如图1 所示。

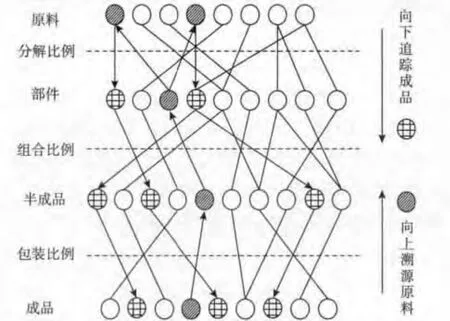
图1 食品加工环节批次分散模型及追溯示意Fig.1 Tracking and tracing model based on batch

图1 中食品加工环节分成原料、部件、半成品、成品4 个层次。模型将加工流程抽象化为分解、组合、包装3 个步骤。在加工流程中，同一种类的不同批次按照优化后的分解比例、组合比例、包装比例加工为成品。当食品质量安全事件发生后，首先根据成品批次，自下而上溯源到原料批次，然后再根据原料批次，自上而下追踪到所有包含该原料批次的成品批次，实现召回。

根据图1 给出的分散批次模型，定义食品加工环节4 个层次批次集合。包括J 个批次的原料R，K个批次的部件C，M 个批次的半成品S，H 个批次的成品F。集合定义如下

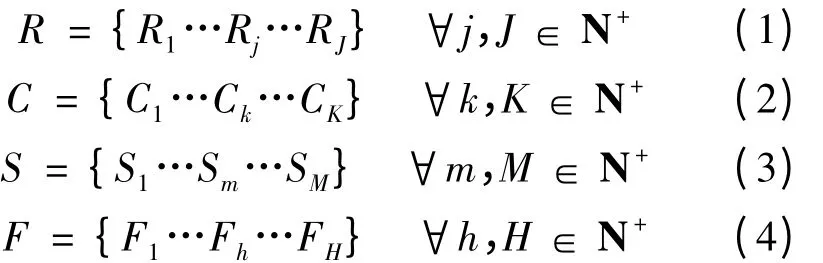
定义从原料Rj到部件Ck的分解比例为RCjk，即Ck占Rj的比例;从部件Ck到半成品Sm的组合比例为CSkm，即Ck占Sm的比例;从半成品Sm到成品Fh包装比例为SFmh，即Sm占Fh的比例。满足如下关系式

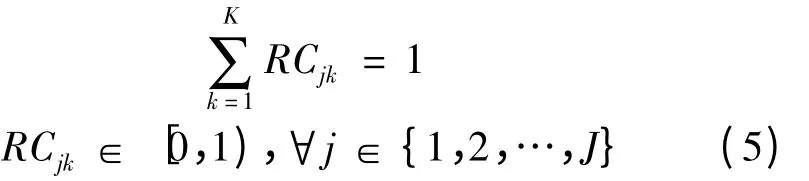
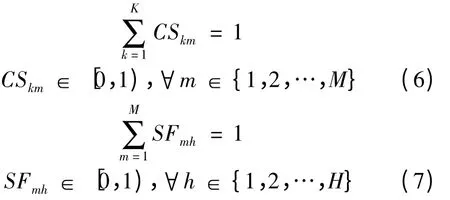
在实际加工环节中，考虑到生产线的效率、仓储容量、人员限制等经济因素，部件与半成品的数量要在一定范围之内［16］。定义部件和半成品数量约束式如下:

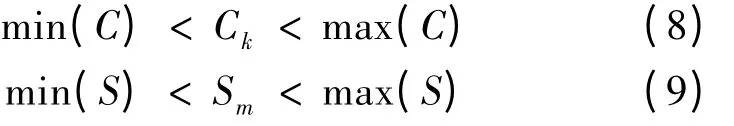
定义从原料到成品的批次分散布尔变量为Bjh，即批次为h 的成品中是否包含有批次为j 的原料。若包含，则布尔变量Bjh 为1，否则为0。同理，定义加工环节相邻层次间的布尔变量分别为，满足以下关系

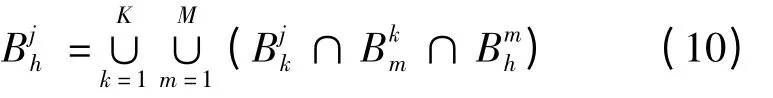
根据Dabbene 等提出的分散批次规模BDC，最坏召回规模定义为

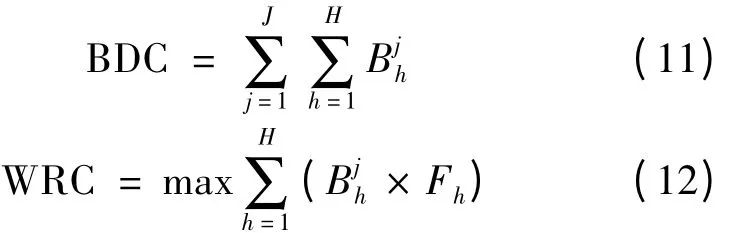
当原料批次Rj出现质量问题时，所有包含该批次原料的成品都需要被召回。定义平均召回规模为

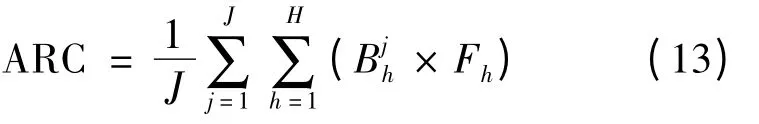
基于以上定义，以平均召回规模ARC 式(13)为目标函数，以式(5)～式(7)为数量等式约束，以式(8)、式(9)为数量不等约束，给出食品供应链加工环节召回优化模型:

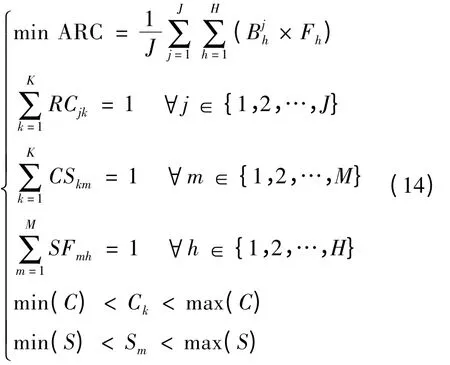
该批次分散模型涉及较多变量和约束，在满足约束的基础上，对批次分散情况进行优化，达到平均召回规模最小的目标。该优化问题为典型NP 难度问题，较难求解，故采用智能算法进行求解。

2 基于人蜂群算法的召回优化策略

2.1 人工蜂群算法模型

人工蜂群算法模型包含3 个要素:蜜源、雇佣蜂、非雇佣蜂［17］。雇佣蜂寻找蜜源，并将信息与其他蜜蜂按概率分享。非雇佣蜂分为跟随蜂和侦查蜂，跟随蜂通过雇佣蜂分享的信息寻找高收益蜜源，侦查蜂随机搜索新蜜源。该模型包含3 种基本行为:蜜源招募蜜蜂，搜索蜜源，放弃蜜源。以上元素组成基本行为模式的自组织过程，本质上是一种通过蜜蜂个体的局部寻优行为凸显全局最优的寻优方式。人工蜂群算法主要步骤如图2 所示。

图2 人工蜂群算法步骤Fig.2 Main steps of the ABC algorithm

设蜜源、跟随蜂、雇佣蜂数量为SN，雇佣蜂重复搜索限制次数LIM，最大迭代次数MCN。首先，根据在搜索空间随机产生SN 个初始蜜源位置(初始解)xp，每个解xp是一个D 维向量。搜索开始后，每个雇佣蜂通过式(15)在初始位置附近随机寻找新蜜源(新解):

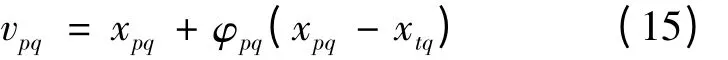
式中vpq为随机寻找新蜜源，t ∈{1，2，…，SN}，q ∈{1，2，…，D}，p 与q 随机选取且p ≠q，φpq为［－1，1］的随机数，对应初始解的fitp邻域。检验新解是否优于旧解，若新解优，则忘记旧解;反之，保留旧解。雇佣蜂完成搜索过程后，返回蜂巢把解的信息和fitp信息共享给跟随蜂，跟随蜂根据式(16)计算每个解的概率:

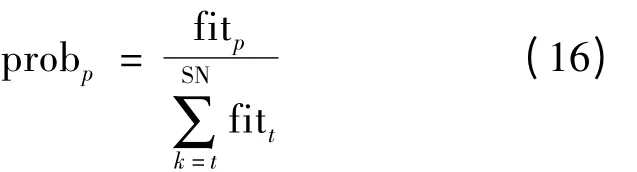
跟随蜂在［0，1］内产生一个随机数，如果解的概率大于该随机数，则跟随蜂根据式(15)产生一个新解，并检验fitp是否比旧解好，记住优解。如果在LIM 次数之内不能改良，则该蜜源被舍弃，同时该雇佣蜂转变成非雇佣蜂。侦查蜂通过式(17)产生一个新蜜源代替被舍弃的蜜源:

同时，该侦查蜂转变成雇佣蜂，重复循环。雇佣蜂进行贪婪算法时，按式(18)进行选择:

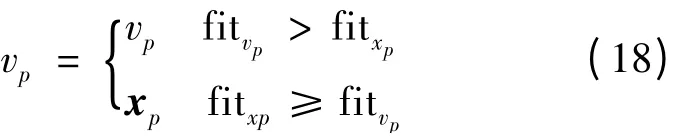
对于优化函数为最大值问题，适应度函数即目标函数;对于优化目标为最小值问题，适应度函数用式(19)表示:

2.2 基于人蜂群算法的召回优化

文中所述的食品供应链召回模型有较多约束，首先将等号约束转化成不等约束，并引入内惩罚函数解决不等约束的问题［18］，设控制误差| hj|≤ω，ω = 0.001，惩罚因子缩小系数γ1，γ2，γ3∈(0，1)，λ1，λ2，λ3，λ4∈(0，1)，将约束转化为无约束优化问题。目标函数如下

式中:Ck为k 批次部件C 的数量;Sm为m 批次半成品S 的数量;λ1，λ2，λ3，λ4为Ck与Sm超出部件和半成品数量约束的惩罚系数。∑RtCab，∑CtSbc，∑StFcd为相邻加工环节批次分散比例之和;γ1，γ2，γ3为比例之和超出范围的惩罚系数。

文中将相邻加工环节的批次分散比例设置为优化变量。图3 为原料RM1，RM2分解成部件CM1，CM3的分散比例，［X1，X2，X3…，X36］为R1，R2，R3，R4，R5，R6分解至C1，C2，C3，C7，C8，C9的批次分散比例矩阵。

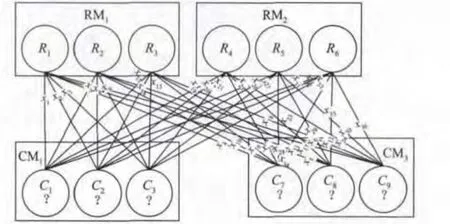
图3 批次分散比例Fig.3 Proportion of batch dispersion

下面给出文中提出的食品召回优化方法的实现步骤:

1)初始化。设置相关参数，雇佣蜂与非雇佣蜂的种群数，蜜源个数，最大循环次数和最大迭代次数。每个蜜源xi代表了一个D 维解，每一维为相邻环节批次分散比例矩阵。

2)依据部件和半成品的数量限制，设置寻优范围，并在寻优范围内产生随机的解。

3)以平均召回规模ARC 为目标函数，并计算各个随机解的适应度值fitxi。标记fitxi最小的值为优秀蜜源。

4)雇佣蜂按式(15)在原蜜源附近寻找新蜜源，并与原蜜源比较，择优标记蜜源。

5)跟随蜂在蜜源中按式(16)选择合适蜜源，并与原蜜源比较，择优标记蜜源。

6)侦查蜂通过式(17)产生一个新蜜源代替被舍弃的蜜源。

7)判断是否达到最大循环次数或者最大迭代次数，如果达到，转至5)，否则转至4)。

8)输出各个批次部件和半成品的数量，即为最优批次分散结果。

3 食品供应链召回算例及优化

分析Dabbene 等给出的算例，针对原料的不同批次进行批次分散优化，能够更加准确地追溯包含某批次原料的成品，并减少召回规模。综合文献［7，10-11］给出的算例，适当调整参数，给出文中算例，对人工蜂群算法进行验证，并进行性能对比。图4 给出了算例分解比例、组合比例、包装比例。其中

R = 12，C = 12，S = 12，F = 12，R1= 16 000，R2= 16 000，R3= 4 000，R4= 2 000，R5= 1 000，R6= 1 000，R7= 20 000，R8= 1 000，R9= 4 000，R10= 5 000，R11= 5 000，R12= 5 000，F1= 5 000，F2= 4 000，F3= 1 000，F4= 15 000，F5= 10 000，F6= 5 000，F7= 5 000，F8= 5 000， F9= 10 000，F10= 5 000，F11= 10 000，F12= 5 000。

图4 召回优化算例Fig.4 Example of batch dispersion optimization

设置MCN = 6 000，LIM = 200，SN = 100，搜索范围为［1 000，20 000］，文中采用人工蜂群算法进行求解。得到如图5 所示的优化后各批次的分散情况。

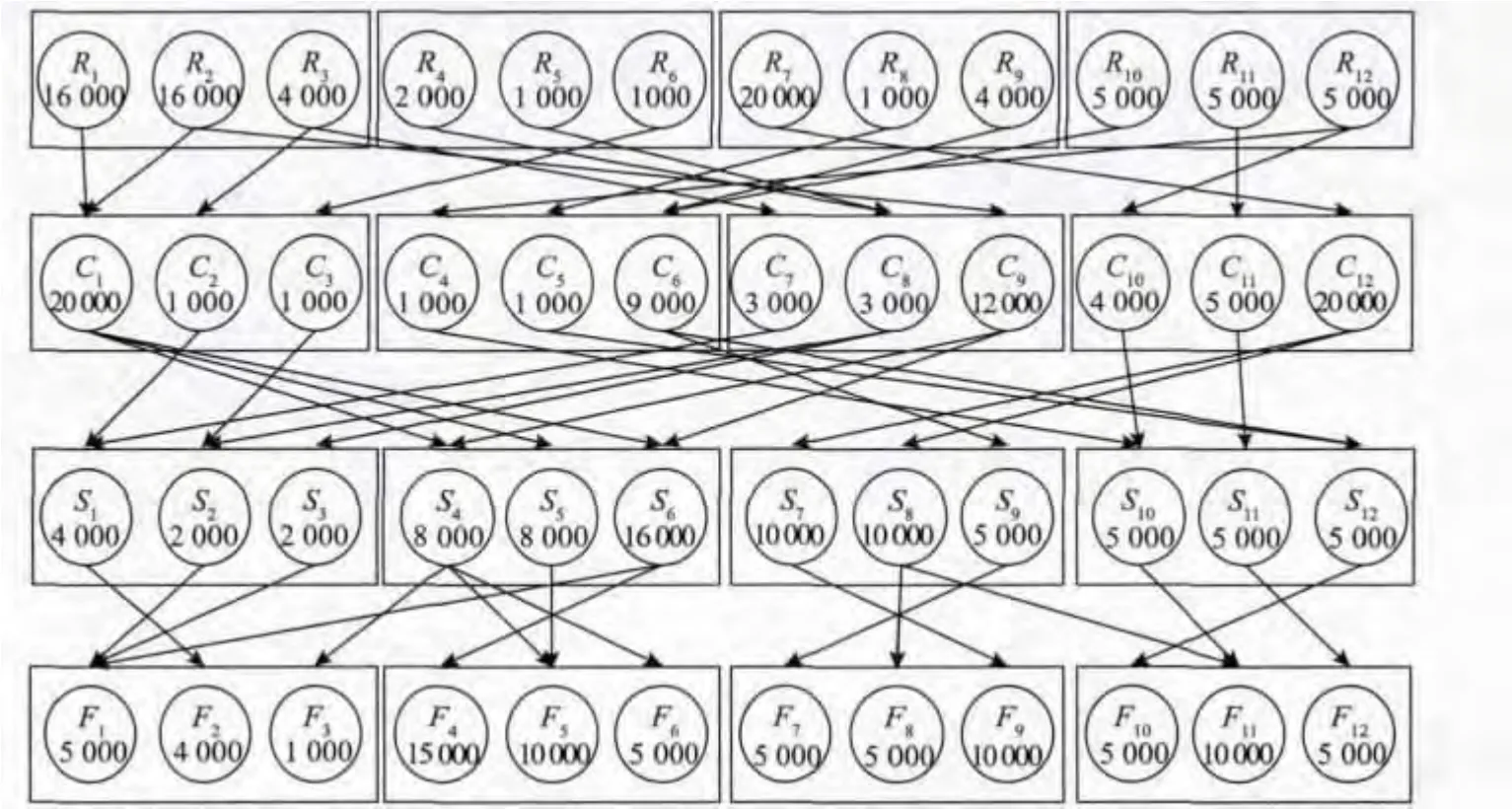
图5 优化后批次分散情况Fig.5 Optimization result of the batch dispersion model

采用人工蜂群算法(ABC)和改进粒子群算法(MPSO)进行优化性能对比。分别对比平均召回规模(ARC)，批次分散规模(BDC)，最坏召回规模(WRC)和运算时间(t)。改进粒子群算法的参数设置与文献［11］相同。比较结果见表1，图6 为2 种算法的平均召回规模收敛曲线。

表1 2 种优化算法性能对比Tab.1 Performance comparison of two algorithms

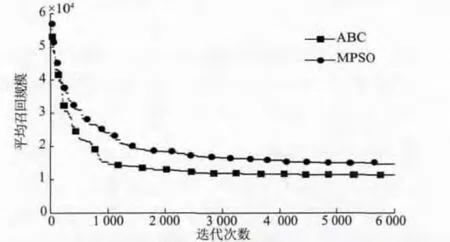
图6 平均召回规模收敛曲线Fig.6 Convergence rate curves of two algorithms

对比平均召回规模ARC，ABC 优化后的平均召回规模为12 750，比MPSO 优化结果降低了14.29%;对比批次分散规模BDC，ABC 的批次分散规模与MPSO 相同;对比最坏召回规模WRC，ABC优化后的最坏召回规模略大于MPSO，考虑到最坏召回发生的可能性较低，且仅比MPSO 大1 000，因此在可接受范围之内;对比运算开销t，ABC 算法运算时间明显小于MPSO，约为MPSO 的38.6%。MPSO 采用了分段门限替换策略，每个迭代周期都根据粒子的适应度函数进行最优粒子替换，因而在进化初期，粒子快速向最优解聚集，而在进化后期(迭代2 000 次之后)，采用了较小的替换门限，粒子的收敛速度减慢，运算开销显著增加(为ABC 算法的2.5 倍左右)。ABC 算法中蜜蜂相互分工与合作，收敛快(迭代1 000 次即趋于最优)、寻优效果好。

4 结 语

针对食品供应链加工环节召回优化的问题，给出了批次分散模型，引入人工蜂群算法优化该模型。与文献［11］提出的MPSO 法相比，文中提出的算法寻优效果好、收敛速度快、复杂度不高，能够有效减少平均召回规模，减小运算开销。对于食品加工企业而言，平均召回成本这个性能指标的重要性远大于最坏召回规模，在其他性能指标有大幅提高的前提下是可以接受的，因此适用于食品供应链召回优化。

［1］Pizzuti T，Mirabelli G，Sanz-Bobi M A，et al.Food track and trace ontology for helping the food traceability control［J］.Journal of Food Engineering，2014，120:17-30.

［2］Dabbene F，Gay P，Tortia C.Traceability issues in food supply chain management:a review［J］.Biosystems Engineering，2014，120:65-80.

［3］Aung M M，Chang Y S.Traceability in a food supply chain:safety and quality perspectives［J］.Food Control，2014，39:172-184.

［4］Alfaro J A，Rábade L A.Traceability as a strategic tool to improve inventory management:a case study in the food industry［J］.International Journal of Production Economics，2009，118(1):104-110.

［5］Kramer M N，Coto D，Weidner J D.The science of recalls［J］.Meat Science，2005，71(1):158-163.

［6］Van Dorp C A. A traceability application based on gozinto graphs［C］//Proceedings of EFITA 2003 Conference. Debrecen，Hungary:IOS Press，2003.

［7］Dupuy C，Botta-Genoulaz V，Guinet A. Batch dispersion model to optimise traceability in food industry［J］. Journal of Food Engineering，2005，70(3):333-339.

［8］Dabbene F，Gay P. Food traceability systems:performance evaluation and optimization［J］. Computers and Electronics in Agriculture，2011，75(1):139-146.

［9］Kallel L，Benaissa M.A production model to reduce batch dispersion and optimize traceability［C］//Logistics (LOGISTIQUA)，2011 4th International Conference on.Hammamet:IEEE，2011:144-149.

［10］Tamayo S，Monteiro T，Sauer N. Deliveries optimization by exploiting production traceability information［J］. Enginering Applications of Artificial Intelligence，2009，22(4):557-568.

［11］李锋，吴华瑞，朱华吉，等.基于改进粒子群算法的农产品召回优化［J］.农业工程学报，2013，29(7):238-245.

LI Feng，WU Huarui，ZHU Huaji，et al. Optimization of agricultural products recall based on modified particle swarm algorithm［J］.Transactions of the Chinese Society of Agricultural Engineering，2013，29(7):238-245.(in Chinese)

［12］Karaboga D.An idea based on honey bee swarm for numerical optimization［R］.Kayzeri:Erciyes University，2005.

［13］张长胜.多目标人工蜂群算法及遗传算法的研究与应用［M］.沈阳:东北大学出版社，2013.

［14］陈久梅.两级定位-路径问题的人工蜂群算法［J］.计算机工程，2014，40(1):172-176.

CHEN Jiumei.Artificial bee colony algorithm for two-echelon location-routing problem［J］.Computer Engineering，2014，40(1):172-176.(in Chinese)

［15］崔明，沈瑾，李延云，等.中国农产品加工技术现状及其推广体系的建设［J］.农业工程学报，2008，24(10):274-278.

CUI Ming，SHEN Jin，LI Yanyun，et al. Status of agricultural product processing technology and construction of its promotion system in China［J］.Transactions of the Chinese Society of Agricultural Engineering，2008，24(10):274-278.(in Chinese)

［16］Dhouib S，Dhouib S，Chabchoub H. Artificial bee colony metaheuristic to optimize traceability in food industry［C］//Advanced Logistics and Transport (ICALT)，2013 International Conference on.Sousse:IEEE，2013:417-420.

［17］雷秀娟.群智能优化算法及其应用［M］.北京:科学出版社，2012.

［18］Karaboga D，Basturk B.On the performance of artificial bee colony (ABC)algorithm［J］.Applied Soft Computing，2008，8(1):687-697.