微生物连续培养单食物链模型的定性分析

王永丽

(江苏财会职业学院 基础部，江苏 连云港222061)

恒化器(Chemostat)是一种用来连续培养微生物的实验装置，可用于模拟湖泊和海洋中单细胞藻类浮游生物的生长，其营养物的输入和流出近似地模拟了自然界的连续代谢过程。Chemostat 模型的研究在废水处理、生物制药及基因产品生产等领域具有重要应用，因此人们对其进行了大量研究［1－6］。文献［1］讨论了单种微生物培养和单营养食物链两种微生物培养的全局稳定性，文献［2］对消耗率参数一次函数的单食物链模型进行了定性研究，文献［3］讨论了三维单食物链种群竞争模型系统解的稳定性。

文中主要考虑三维单食物链种群模型。假设被捕食者种群对营养基消耗率的参数δ1推广为二次函数δ1= A +Bs2，捕食者种群对被捕食者种群消耗率的参数δ2推广为一次函数δ2= C + Dx1;捕食者种群对被捕食者种群的关系，以及被捕食者种群与养料浓度的关系都取为Monod 类型，对系统进行定性分析，并通过定性分析证明系统平衡点的存在性和稳定性，以及系统正向不变集的存在性。

1 变消耗率的单食物链模型

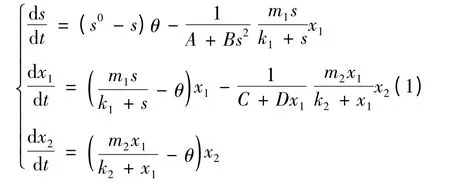
变消耗率恒化器中消耗率参数为δ1= A +Bs2，δ2= C + Dx1的3 种微生物组成的单食物链模型可由如下常微分系统给出:其初始条件为s(0)= s0≥0，xi(0)= xi0≥0(i =1，2)。其中，s，xi分别代表营养基和第i 种微生物在t 时刻的浓度;参数θ 表示营养基输入输出量;s0为供液源流中营养基的浓度;1/δi代表捕食者微生物xi对被捕食者微生物xi－1的消耗率(i = 1 时，被捕食者微生物为s)，在恒定的环境下，它们都是常数;mi＞0，ki＞0 分别代表第i 种微生物的最大增长率和半饱和常数。令

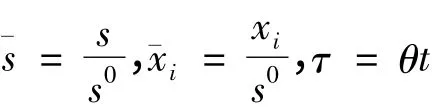
对系统(1)作无量纲变换，并记

变换 后 仍 以s，xi，t，mi，ki记。则 系 统(1)变为如下系统(2)，且必有s(t)≤1。

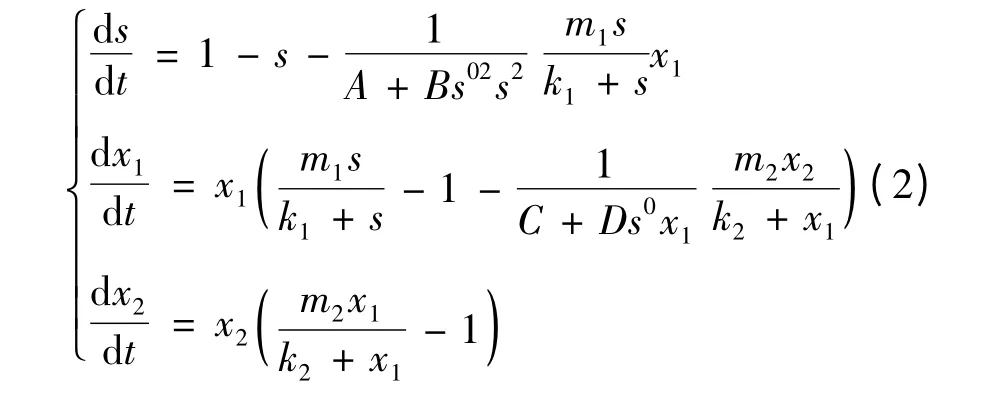
考虑系统(2)的平衡点，为此解方程组

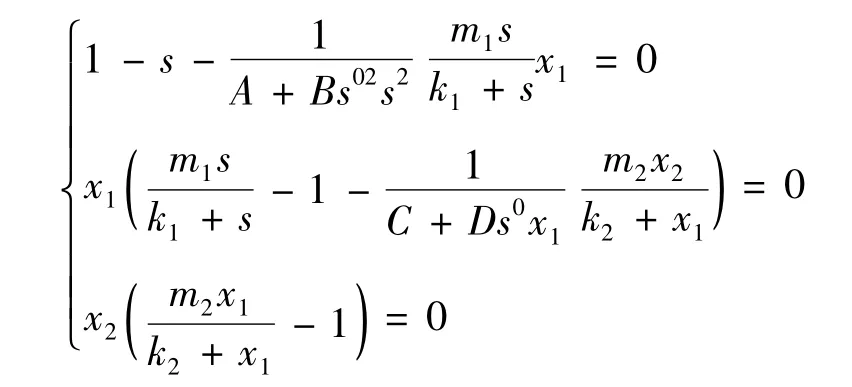
其中

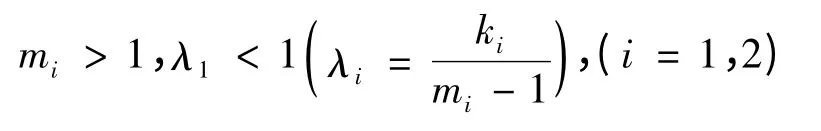
得系 统(2)的 平 衡 点E0(1，0，0)，E1(λ1，(1 －λ1)(A+Bs02)，0)，E2(s*，λ2，)，其中s*，满

足如下方程:

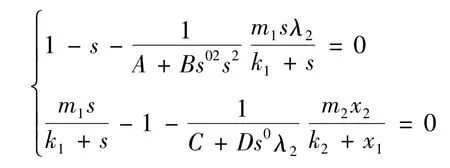
整理方程组得

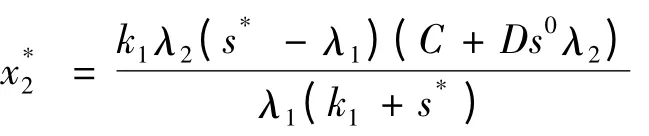
并且只要s*－λ1＞0，就能保证为正，并且s*满足下面方程:

因为f(1)= m1λ2＞0，f(0)= －k1A ＜0，所以方程(3)在区间(0，1)至少存在一个正解。通过对f(s)进行高阶求导，可以得到两个命题:

命题1 在k1＞1，s02时，函数f(s)在区间(0，1)内存在惟一正解，所以对系统(2)来说，正平衡点E2是惟一的;

命题2 在

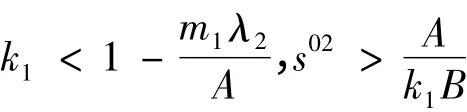
时，函数f(s)在区间(0，1)内存在惟一正解，所以对系统(2)，正平衡点E2是惟一的。

文中将就命题1，2 中这两个条件，分别对系统(2)的3 个有限远平衡点E0，E1，E2的稳定性展开讨论。

1.1 平衡点E0 的稳定性

平衡点E0(1，0，0)对应的特征方程的特征根

所以平衡点E0为鞍点，不稳定。

1.2 平衡点E1 的稳定性

对平衡点E1(λ1，(1 － λ1)(A + Bs02)，0)特征方程为

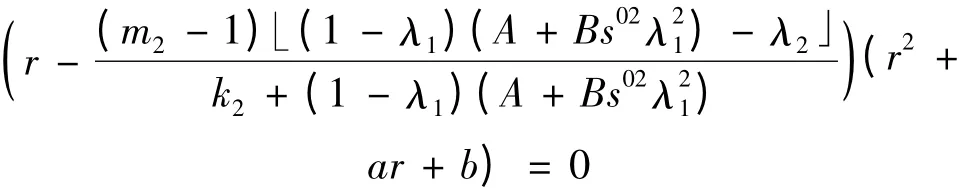
特征根

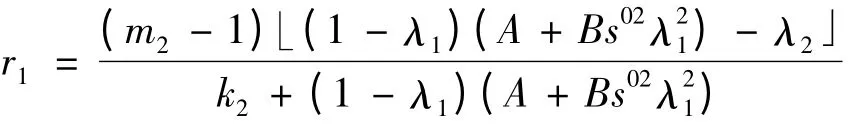
在(1 －λ1)(A +Bs02)＞λ2时，r1＞0，此时，E1是不稳定的平衡点;在(1 －λ1)(A +Bs02)＜λ2时，r1＜0，此时E1的稳定性与二次方程r2+ar +b = 0的根r2，r3的符号有关，这里

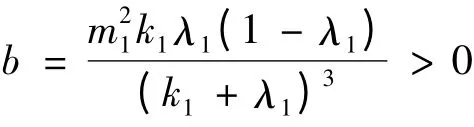
其中，g(k1，λ1，m1) = (k1+ 2λ1)m1(1 － λ1)－(k1+λ1)2，因为k1+ λ1= m1λ1，k1+2λ1= (m1+1)λ1，所以可将g(k1，λ1，m1)整理为

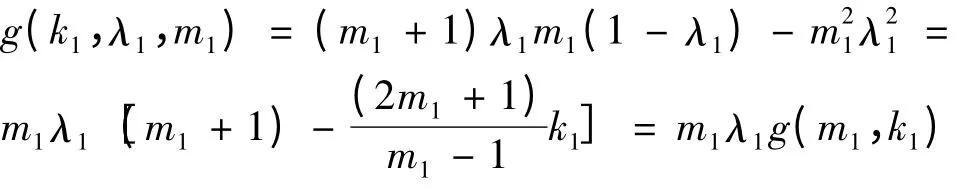
其中

1)当m1∈(1，1 +」时，分别在命题1，2 的条件下，讨论r2+ ar + b = 0 中的a 的符号。

首先讨论h(m1)－1 符号。当m1∈(1，1 +」时，－2m1－2 ≤0，故h(m1)－1 ≤0 即h(m1)≤1。

命题1 中条件k1＞1。所以有h(m1)－ k1＜0，从而h(m1，k1) ＜ 0。故g(k1，λ1，m1) = (k1+2λ1)m1(1 － λ1)－ (k1+ λ1)2＜0，所以a ＞0。

命题2 中条件k1＜1。h(m1)与k1的大小需另行讨论。

(1)当h(m1)＜k1，即时，此时仍

有a ＞0。

(2)当h(m1)＞k1，即时，g(k1，λ1，m1)= (k1+2λ1)m1(1 －λ1)－(k1+λ1)2＞0，所以a 的符号还取决于培养液的初始浓度s0:

1)当

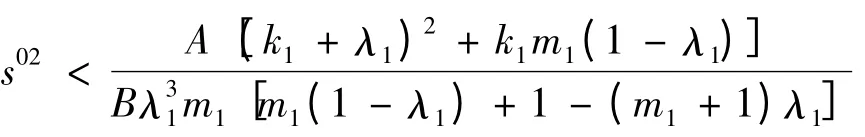
时，a ＞0;

2)当

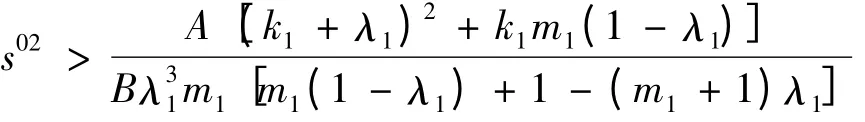
时，a ＜0。

在a ＞0 时，又因为有b ＞0，所以特征根r2，r3均有负实部，此时平衡点E1是稳定的;

在a ＜0 时，特征根r2，r3均有正实部，从而平衡点E1是不稳定的。

因为在命题2 中有条件s02＞，所以还要注意比较与

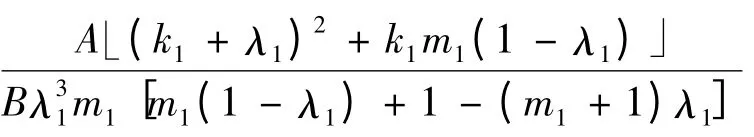
的大小。

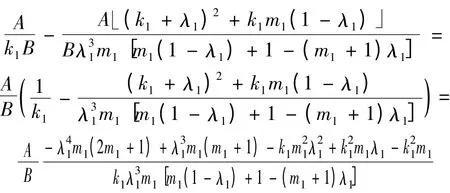
其中λ1∈(0，1)。令

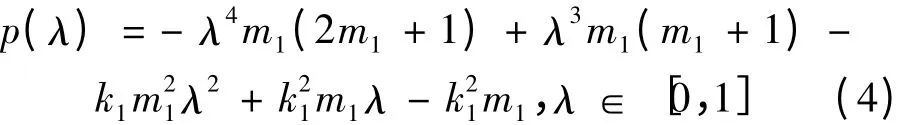
通过对p(λ)求一到三阶导数及对端点的求值等一系列运算可得:当k1∈(0，1)，λ ∈［0，1］时，在λ 与p(λ)构成的坐标系中，有3 种可能情况:函数p = p(λ)的曲线完全在λ 轴之下，即p(λ)＜0;函数p = p(λ)的曲线除最高点在轴上之外，其余的完全在λ 轴之下，即p(λ)≤0;函数p = p(λ)的曲线最高点在λ 轴之上，即p(λ)的图像与λ 轴有两个交点，不妨设为λ1，λ2且λ1，λ2∈(0，1)，在(λ1，λ2)内p(λ)＞0，在(0，λ1)(λ2，1)两个区间内p(λ)＜0。事实上，在p(λ)＜0 时，有

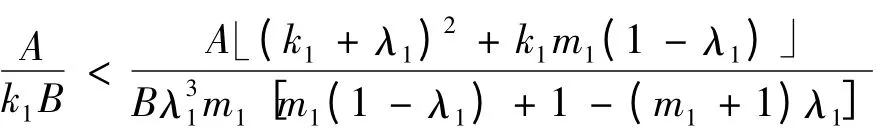
在p(λ)＞0 时，有

当

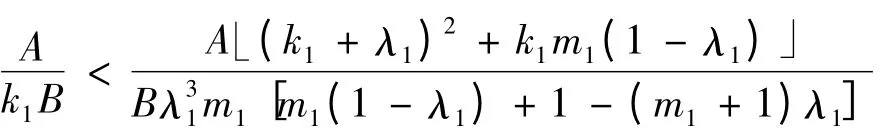
成立时

1)中初始浓度范围

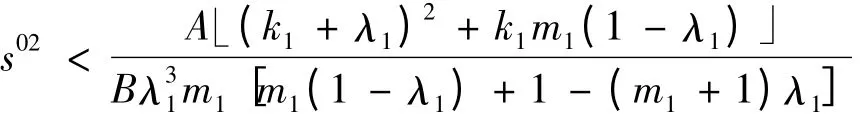
需改为

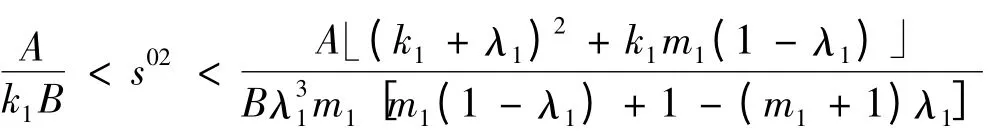
此时仍有a ＞0;

2)中初始浓度范围不变，仍为仍有a ＜0;

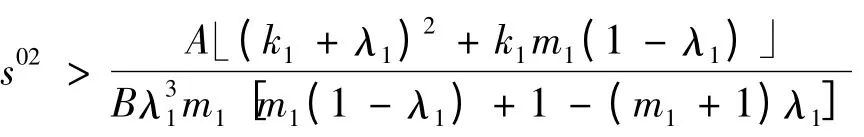
当

成立时:情况1)不存在;情况2)中初始浓度范围取为s02＞，仍有a ＜0。

在a ＞0 时，又因为有b ＞0，所以特征根r2，r3均有负实部，此时平衡点E1是稳定的;在a ＜0 时，特征根r2，r3均有正实部，从而平衡点E1是不稳定的。

2)当m1∈(1 +，+ ∞)时，分别在命题1，2的条件下，讨论r2+ ar + b = 0 中a 的符号。当m1∈(1 +，+ ∞)时，－ 2m1－ 2 ＞0，故h(m1)－1 ＞0，即h(m1)＞1。

在命题1 中，k1＞1，所以h(m1，k1)的符号决定于h(m1)与k1的大小。

(1)当h(m1)＜k1，即时，此时仍有a ＞0;(2)当h(m1)＞k1，即时，g(k1，λ1，m1)= (k1+2λ1)m1(1 －λ1)－(k1+λ1)2＞0，所以a 的符号还取决于培养液的初始浓度s0:

1)当

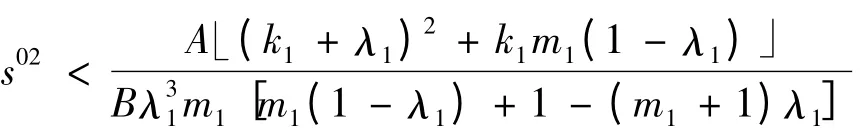
时，a ＞0;

2)当

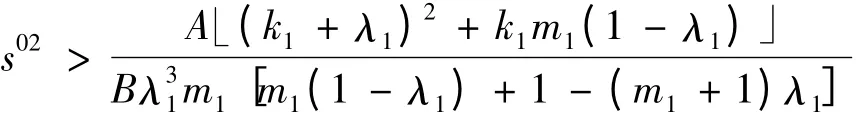
时，a ＜0。因为在命题1 中，要求s02＜，所以仍需比较与

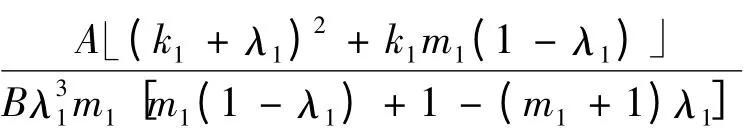
的大小。比较过程见1)。

在命题2 中，k1＜1 所以h(m1，k1)＞0。所以a的符号还取决于培养液的初始浓度s0:

1)当

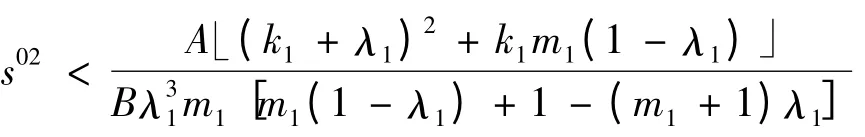
时，a ＞0;

2)当

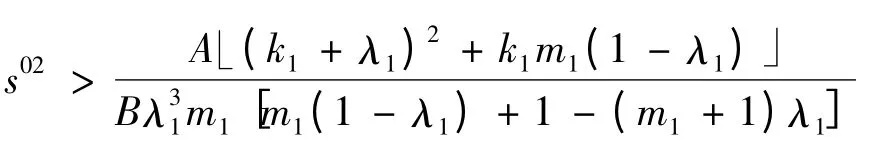
时，a ＜0。比较过程见1)。在a ＞0 时，又因为有b ＞0，所以特征根r2，r3均有负实部，此时平衡点E1是稳定的;在a ＜0 时，特征根r2，r3均有正实部，从而平衡点E1是不稳定的。

1.3 平衡点E2 的稳定性

在平衡点E2(s*，λ2，)处，对应的特征方程为r3+ ar2+ br + c = 0，其中a = β － φ:

当

时，φ ＞0。

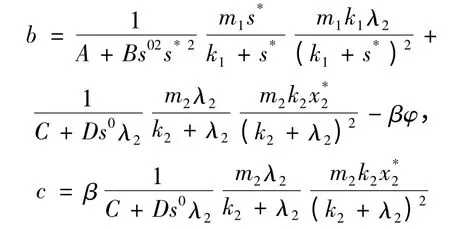
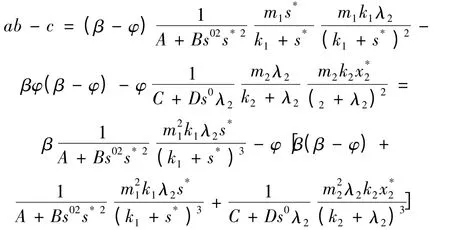
而在β ＞φ 时，一定有

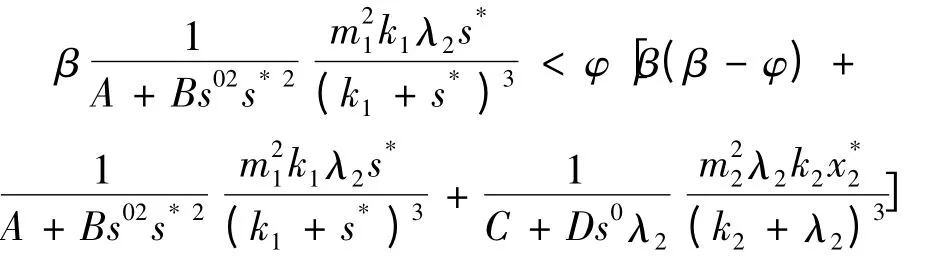
即ab － c ＜0 成立，此时能保证E2不是渐进稳定的平衡点。

2 相关结论

定理1 系统(2)的平衡点E0为鞍点，不稳定;在满足条件(1 － λ1)(A + Bs02)＞λ2时，平衡点E1也是不稳定平衡点。

定理2 在条件(1 － λ1)(A + Bs02)＜λ2下，当m1∈(1，1 +」时

1)若满足k1＞1 且，则平衡点E1是稳定的;若满足且则平衡点E1是稳定的;若满足

且初始浓度s0满足条件

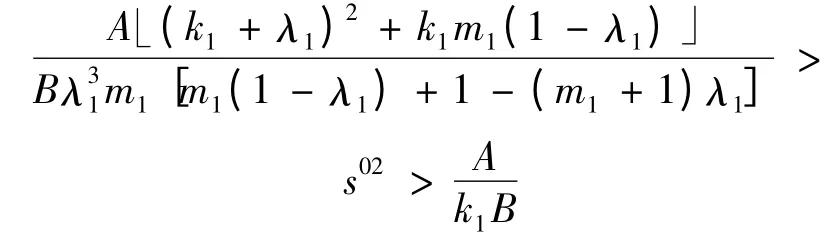
时，平衡点E1是稳定的;2)若满足

且

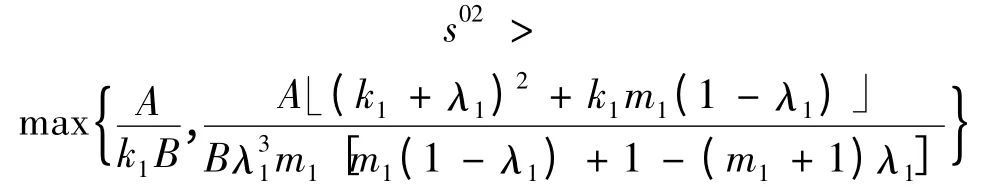
时，平衡点E1是不稳定的。

定理3 在条件(1 － λ1)(A + Bs02)＜λ2下，当m1∈(1 +，+ ∞)时

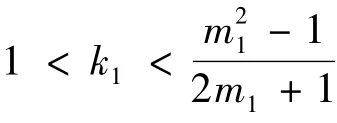
或者k1＜1 且有初始浓度s0满足条件

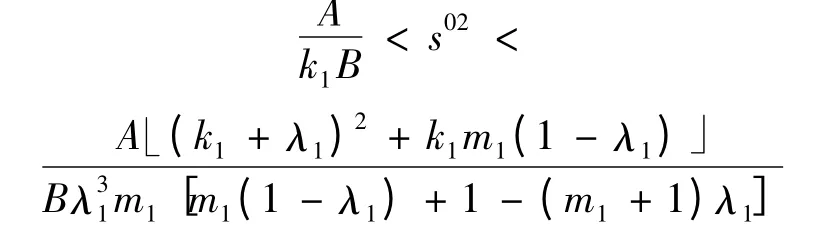
则平衡点E1是稳定的;3)若满足

或者k1＜1 且初始浓度s0满足条件

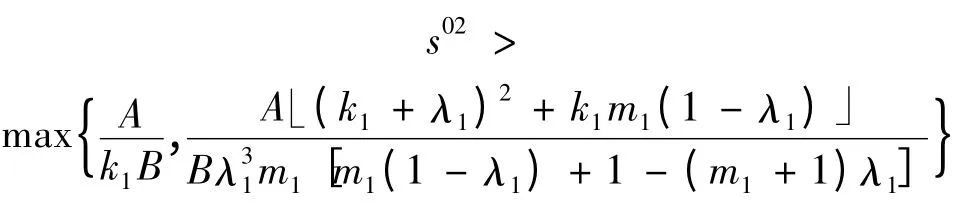
则平衡点E1是不稳定的。

定理4 系统(2)存在正向不变集

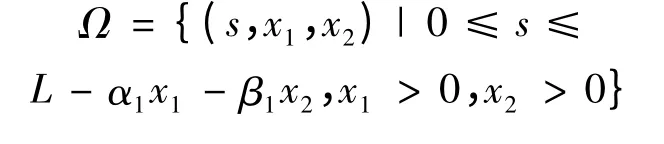
其中

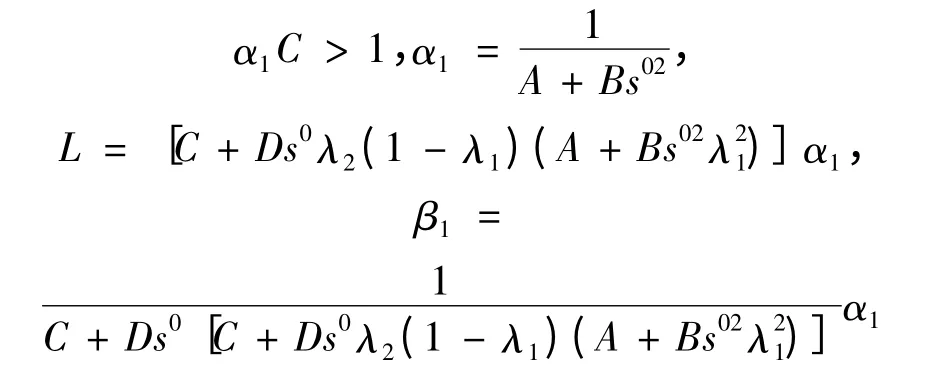
即R3+内任意点(s，x1，x2)出发的轨线，当t →+ ∞时，终将进入集合Ω。

证 系统(2)存在解平面x1= 0 及x2= 0。下面考察平面。所以系统(2)的轨线当t 增加时是由区域Ω1= {(s，x1，x2)| s ＜0，x1＞0，x2＞0}穿过平面s = 0 而进入区域Ω 内。再考虑平面F = s + α1x1+ β1x2－ L = 0。

因为0 ＜s(t)≤1，所以有

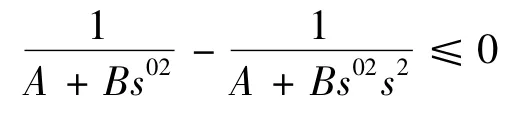
又因为平面F 与x1轴相交于，所以必有

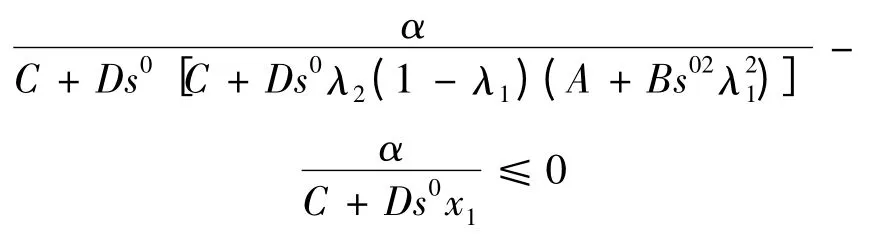
成立。所以在满足条件α1C ＞1，即

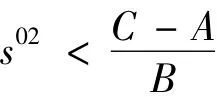
时，有

则系统(2)的轨线通过平面F = 0 时，是由外向内进入区域Ω。即任意从(s，x1，x2)出发的轨线，当t→+ ∞时，不会穿过F = 0 跑出区域Ω。综上所述，Ω为系统(2)的不变区域。

因为在(1 － λ1)(A + Bs02λ21)＞λ2时，有r1＞0，此时E1是不稳定的平衡点;而在对E2的讨论中又知，在

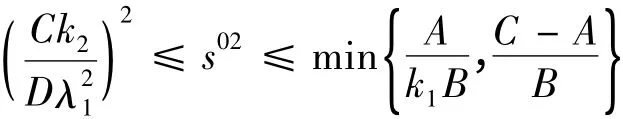
时，E2不是渐进稳定的平衡点，所以在时，在系统(2)的正向不变集中，在平衡点E2的附近必存在正向吸引子。由于正向吸引子不是平衡点，因此在恒化器中微生物浓度会产生振荡，但不一定是周期振荡。

3 结 语

研究了一类变消耗率单食物链模型，分析了其平衡点的类型及各个平衡点的稳定性，并证明系统存在正向不变集。由此可见，对于此类模型，当参数满足一定条件时，同时培养两种微生物且使微生物种群共存这一目的是可以实现的。

［1］庞国萍，陈兰荪. 比例确定增长率Chemostat 模型的全局稳定性［J］. 广西师范大学学报:自然科学版，2006，24(1):37－40.

PANG Guoping，CHEN Lansun.Global stability of chemostat models with ratio－dependent increase rate［J］. Journal of Guangxi Normal University:Natural Science Edition，2006，24(1):37－40.(in Chinese)

［2］刘婧，杨淑芹.恒化器中微生物连续培养单食物链模型的定性分析［J］.大连海事大学学报，2004，30(3):88－91.

LIU Jing，YANG Shugin.Qualitative analysis for the single food chain model of microorganism continuous culture in chemostat［J］.Journal of Dalian Maritime University，2004，30(3):88－91.(in Chinese)

［3］凌志超，张天四.恒化器中一类具有非常数消耗率微生物培养模型的定性分析［J］. 上海理工大学学报，2012，34(4):373－376.

LING Zhichao，ZHANG Tiansi. Qualitative analysis for a class of microbial continuous culturemodel with variable yield in chemostat［J］.Journal University of Shanghai for Science and Technology，2012，34(4):373－376.(in Chinese)

［4］刘三红.一类具有时滞的恒化器模型的定性分析［J］.佳木斯大学学报:自然科学版，2012，30(2):295－296.

LIU Shanhong.Qualitative analysis of a chemostat model with time delay［J］. Journal of Jiamusi University:Natural Science Edition，2012，30(2):295－296.(in Chinese)

［5］付桂芳，马万彪.由微分方程所描述的微生物连续培养动力系统(1)［J］.微生物学通报，2004(31):136－139.

FU Guifang，MA Wanbiao.Chemostat dynamics models described by differential equations［J］. Microbiology China，2004(31):136－139.(in Chinese)

［6］刘婧，刘卫强.恒化器中具有不同移动速率的环状模型解的定性分析［J］.大连海事大学学报，2007，33(2):116－119.

LIU Jing，LIU Weiqiang.Qualitative analysis of solution in chemostat with different removing rate［J］.Journal of Dalian Maritime University，2007，33(2):116－119.(in Chinese)

［7］郑承民，刘芳园.恒化器中两种群适应性生长模型［J］.数学的实践与认识，2011，41(8):92－102.

ZHENG Chengmin，LIU Fangyuan.The models of two populations with adaptive nutrient uptake in a chemostat［J］.Mathematics in Practice and Theory，2011，41(8):92－102.(in Chinese)

［8］马知恩，周义仓.常微分方程定性与稳定性方法［M］.北京:科学出版社，2001.