一种新的光伏系统最大功率跟踪控制方法

赵 志

（湖南大学电气与信息工程学院，长沙 410082）

引言

随着经济社会的发展，能源的需求和消耗与日俱增，传统化石能源日益走向衰竭，且传统化石能源的大量使用，已造成严重的环境问题，寻找新的可再生清洁能源已迫在眉睫。太阳能具有储量大、绿色无污染、无需开采和运输等众多优点，受到广泛的关注。光伏发电是太阳能主要利用方式之一［1-2］。目前制约光伏发电发展的主要原因之一是发电成本过高。提高发电效率，可间接地降低发电成本，促进光伏产业的发展。控制光伏组件始终工作在最大功率点处，是提高光伏发电效率的最有效方式之一，因此如何快速地实现跟踪最大功率点跟踪 MPPT（maximum power point tracking）成为光伏发电的研究热点。

目前最大功率跟踪控制方法主要有：恒定电压法［3］、电导增量法［4-5］和扰动观察法［6-7］。 恒定电压法是控制光伏组件工作在某一固定电压，控制方法和硬件电路简单，但是由于最大功率点会随着外界环境的变化而变化，因此会造成功率的大量流失；电导增量法是通过测量光伏组件的瞬时电导（I/U）和增量电导（dI/dU）来调节光伏组件的工作点，控制效果好，但是对硬件电路的精度要求高，系统成本大，不适合大范围使用；扰动观察法是通过电压扰动来比较扰动前后功率的大小来调节光伏组件的工作点，控制思路简单，控制效果较好，成本相对较低，因此被广泛应用。

本文依据扰动观察法的控制思想，结合大型光伏场中光伏组件的特性，提出一种新的最大功率跟踪控制方法。该方法能在大型的光伏电场中大幅度降低成本，具有较好的实际应用价值。本文首先介绍了该方法的原理，然后通过仿真验证了该方法理论的正确性，并与扰动观察法控制效果作了比较，最后通过实验进一步验证了该方法的可行性。

1 原理

大型光伏场一般选择日照充足，周围环境理想的场所［8］。局部阴影的形成主要源于云层遮挡和杂物覆盖。从宏观来说，对整个光伏系统确实存在局部阴影的问题［9-10］；从微观来说，可以认为相邻2个组件出现差异化的概率很小，也就是2个组件的伏安特性曲线相同，最大功率点也相同。

为了实现最大功率跟踪控制，假设组件A、B相邻，其功率-电流特性曲线如图1所示。在最大功率点处，dP/dI=0，以差分形式表示为

式中，P（I）和 P（I+ΔI）分别为光伏组件输出电流为 I和I+ΔI时的输出功率；ΔI为两光伏组件输出电流之差，是一个很小的量。式（1）化简得到

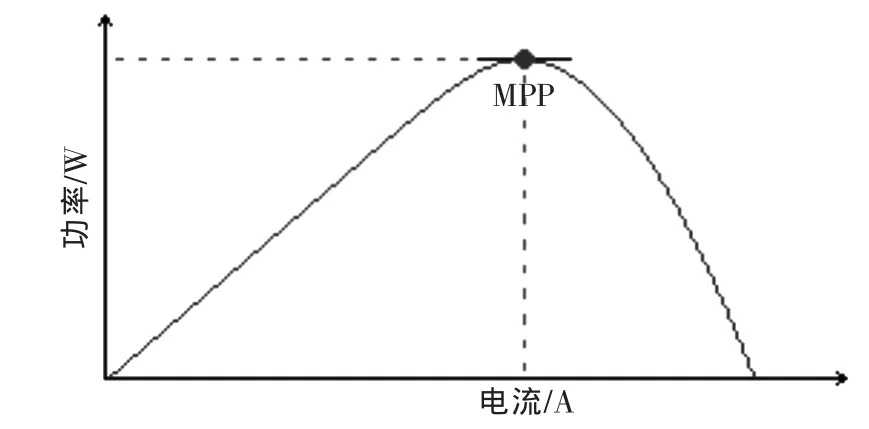
图1 光伏组件功率－电流曲线Fig.1 Power-current curve of PV module

为了省去存储器，应在每一个采样周期内能同时获得 P（I）和 P（I+ΔI）值，这需要考虑两个方面：一是如何测量功率；二是如何同时实现组件的输出电流为I和I+ΔI。 一种典型的光伏并网系统主电路结构如图2所示。对于第一个方面，组件A、B经Boost电路后，在任意时刻的输出电流相等，因此只需检测其输出电压进行比较，当输出电压相等时表示其输出功率也相等；对于第二个方面，由于组件A、B经过Boost电路后输出电流相等，为此，只需将两组件Boost电路的占空比设置一个较小的差值ΔD即可。

图2 光伏并网系统主电路结构Fig.2 Grid-connected PV system structure

假设Boost电路A的占空比为DA=D，Boost电路B的占空比DB=D+ΔD。此时，组件A、B的输出电流分别为

式中，IA为组件A的输出电流；IB为组件B的输出电流；Iout为Boost电路的输出电流；ΔD为两组件的占空比之差。

当ΔD足够小时，即可实现组件A和组件B的工作电流相差一个很小值，即

因此，适当调节占空比D，控制Boost电路A的占空比为D，Boost电路B的占空比为D+ΔD，即可控制光伏组件A、B的输出电流分别为I和I+ΔI，这样就满足了第二个方面的条件，其中ΔI的大小由ΔD决定。

图3 最大功率跟踪控制结构Fig.3 Maximum power tracking control structure

由于光伏组件A的输出电流始终比光伏组件B的输出电流大ΔI，因此组件A的工作点始终在组件B的右侧。对两Boost电路的输出电压UA和UB进行采样，最大功率跟踪控制结构如图3所示，通过对UA和UB作差，将差值通过适当调整，转化为相应的占空比，动态调节光伏组件的工作点，使光伏组件最终工作在最大功率点处。光伏组件A、B的不同工作状态如图4所示。具体调节过程如下。

（1）当 UA＞UB即 PA＞PB时，此时 A、B 两组件同时工作在最大功率点的左侧，如图4（a）所示。将二者的差值经PI调节器后，占空比D减小，光伏组件的输出电流增大，工作点向右移动，逐渐向峰值靠拢。

（2）当 UA＜UB即 PA＜PB时，此时 A、B 两组件同时工作在最大功率点的右侧，如图4（b）所示。将二者的差值经PI调节器后，占空比增大，光伏组件的输出电流减小，工作点向左移动，逐渐向峰值靠拢。

（3）当UA=UB时，此种情况只发生在刚刚启动或者已经工作在最大功率点时。在刚刚启动时，若UA=UB，此时PI调节器输出为0，A、B两组件占空比分别为0和ΔD；又因为启动时，光伏组件的输出电压相等，此时两Boost电路的输出电压会因为ΔD而产生一个差值ΔU，这样PI调节器又进入工作，进行调节。

（4）最终组件A工作在峰值右侧，组件B工作在峰值左侧，如图4（c）所示，此时UA=UB，两光伏组件的输出功率相等。虽然此时两组件没有工作于理想最大功率点处，但由于ΔI值很小，其工作点很接近于理想的最大功率点，因此可近似认为光伏组件工作于最大功率点处。

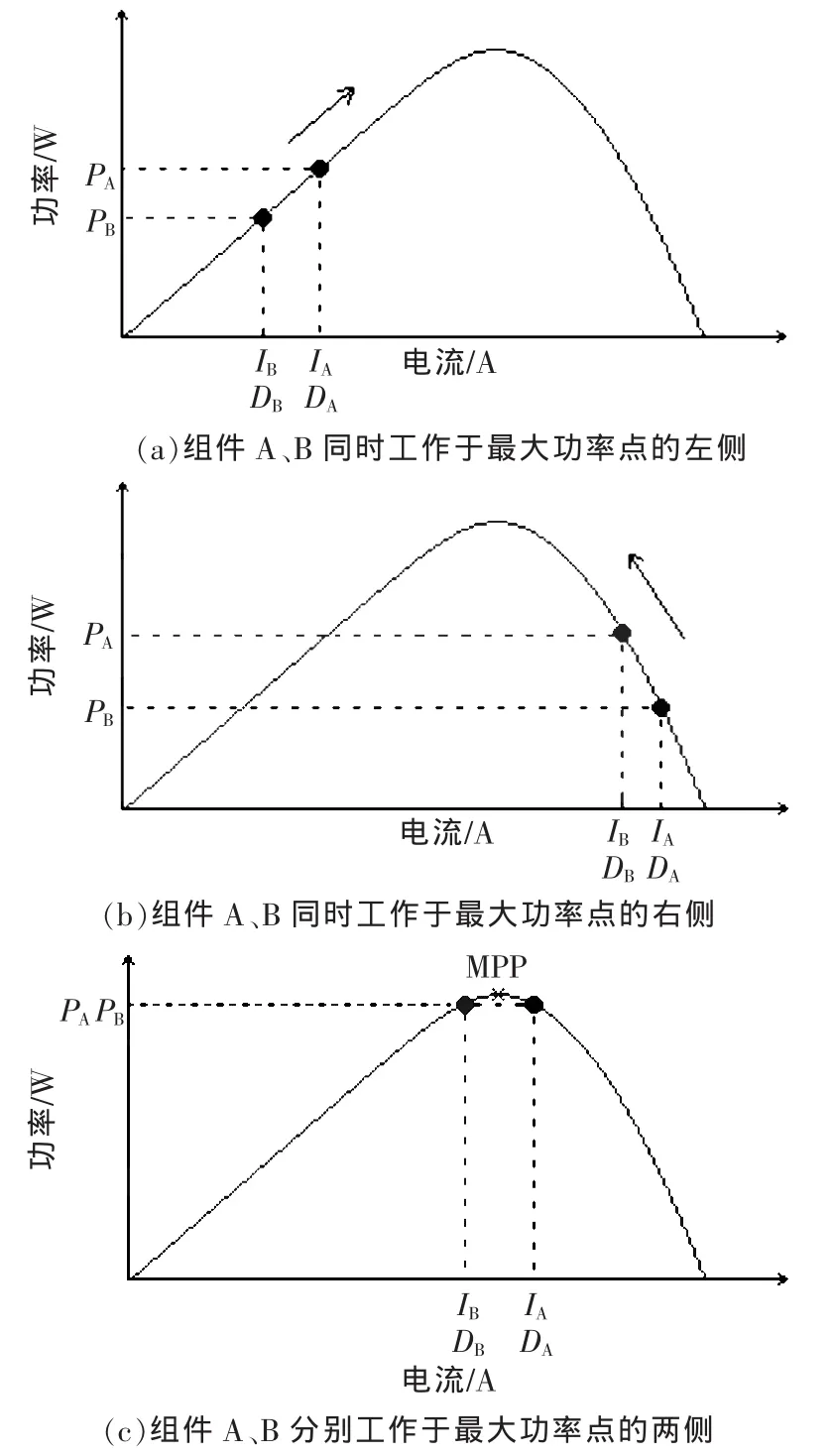
图4 光伏组件A、B的3种不同工作状态Fig.4 Three different working states of PV modules A and B

ΔD值的大小决定了ΔI值的大小，ΔI的大小决定了两光伏组件功率相等时与实际最大功率点的逼近程度。对于一个确定的光伏并网系统而言，其逆变器直流侧电压UDC为一恒定值，光伏组件的工作电压UPV的变化范围不大，因此占空比D=UDC/UPV变化范围也不大。 由式（5）知，稳定时ΔI≈ΔD/D·Im，Im为光伏组件最大功率点处的输出电流，可由光伏组件铭牌参数读出。因此对于给定ΔI值，可以大致估算出 ΔD。 本文中 ΔD=0.01，稳态时 ΔI≈0.07 A。

从图4（c）中可以看出，稳定时组件的工作点接近于理论最大功率点，但并不重合，其差值取决于ΔD的大小，当ΔD逐步减小时，组件A和B的工作点都向理论最大功率点靠拢，当ΔD趋近于0时，组件A和B都达到理论最大功率点。但工程中，ΔD过小将会使得调节过程变长，动态性能降低。

同时需要提出的是，本文提出的方法与直接将两组件串联后再用一个Boost电路来实行最大功率跟踪相比，多了一个Boost电路，两Boost电路不共地，驱动电路势必要多一路独立电源，但是本文提出方法省去了电流传感器，省去了微处理器，从成本上比较，两结构相当。从使用寿命上比较，两组间串联使用一个Boost电路，开关管容量增加，承受的电压增大，单管承受的开关损耗增加，使用寿命减短。从控制方法上比较，本文方法省去电流采样和功率的计算，不需要对上个周期的功率、电压和电流进行存储，控制上具有更强的实时性和快速性，仅用简单的模拟电路就可以实现跟踪控制，更稳定。整体来讲，本文方法具有一定的研究价值。

2 可行性验证及性能对比仿真

为了验证本文所提出最大功率跟踪方法的有效性，本文选用2个参数相同的光伏组件组成一条串联支路，然后并入光伏系统中，光伏组件模型采用单二极管模型［11-12］，其参数如表1所示。

表1 光伏组件参数Tab.1 PV module parameters

仿真比较本文提出的MPPT方法与扰动观察法在光照充足和光照不足两种不同光照下的性能，仿真时本文MPPT方法中ΔD=0.01，扰动观察法扰动步长设为0.2 V，仿真结果如下。

（1）A、B两块光伏组件的光照强度都设定为1 000 W/m2，温度25℃。本文MPPT方法和扰动观察法的仿真结果如图5所示。采用本文提出MPPT方法，测得的输出功率如图5（a）所示，稳态时输出功率187 W，占空比平均值为0.41；扰动观察法测得的输出功率如图5（b）所示，稳态时输出功率为181 W，占空比平均值为0.38。从图5中可看出，该MPPT方法比扰动观察法响应速度更快，波动更小；同时，由于本文所提出的方法省去了功率计算环节，在光伏组件实际工作点离最大功率点越远，相应的ΔU越大，同时光伏组件工作点靠近最大功率点的速度就越快，类似于变步长扰动观察法［13］，但比变步长扰动观察法简单得多。

图5 光照强度为1 000 W/m2时2种方法的功率仿真曲线Fig.5 Power simulation curves of two methods in intensity of 1 000 W/m2

（2）A、B两块组件的光照强度设定为500 W/m2，温度25℃。本文MPPT方法与扰动观察法的仿真结果如图6所示。采用本文所提出的MPPT方法，测得的输出功率如图6（a）所示，稳态时输出功率有效值为127 W，占空比平均值为0.47；扰动观察法测得的输出功率如图6（b）所示，稳态时输出功率为121 W，占空比平均值为0.49。观察图6可以看出，在调节初期2种方法测得的功率都出现了震荡。因为在低光照时，PI调节器容易陷入积分饱和，但是本文提出MPPT方法比扰动观察法调节速度快，因此能更快跳出震荡，进入稳定。同时这种震荡也使得扰动观察法比本文提出MPPT方法输出功率略低。

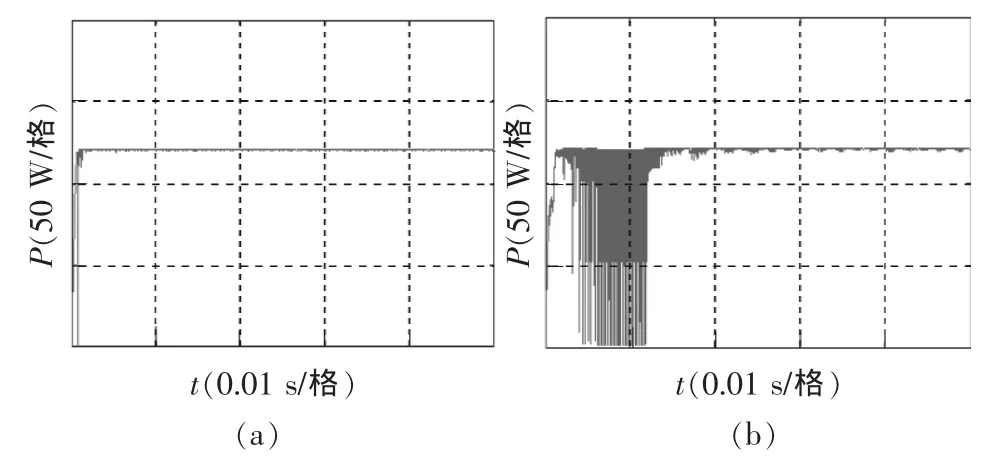
图6 光照强度为500 W/m2时2种方法功率仿真曲线Fig.6 Power simulation curves of two methods in intensity of 500 W/m2

（3）仿真分析本文提出MPPT方法的抗阴影扰动能力。仿真初始时刻设组件A、B的光照强度都是 1 000 W/m2，0.2 s时组件 A光照强度降到 600 W/m2，0.4 s时，组件A的光照强度重新变为1 000 W/m2。仿真开始后，最大功率跟踪控制模块迅速介入，输出功率达到183 W；0.2 s后，组件 A光照强度降低时，限幅模块开始工作，占空比限制在0.67，输出功率为55 W；0.4 s后，最大功率跟踪控制模块重新起作用，功率输出恢复到183 W。输出功率曲线如图7所示。

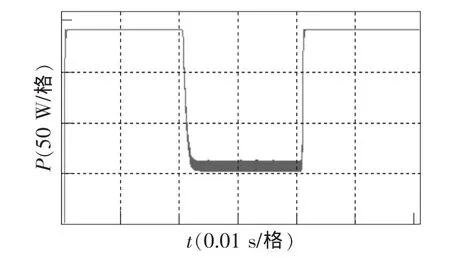
图7 阴影扰动时输出功率曲线Fig.7 Output power curve in shadow disturbance

通过以上仿真可以得出结论，本文提出的MPPT方法，能快速有效地跟踪最大功率，有较好的抗干扰能力和稳定性。需要特别说明的是，当A、B光伏组件光照不一致时，最大功率跟踪控制可能会失效，当外界干扰消除后，控制系统能恢复对最大功率点的跟踪。但对于大型光伏电场，云层等形成的局部阴影恰巧使两相邻光伏组件出现光照不一致的情况概率较小，而且云层等造成的局部阴影能较快自行恢复。同时通过对光伏电池适当的组配，可以减小光伏组件的不一致性［14］，从性价比而言，本文提出的MPPT方法仍是有很大的优势。

3 硬件实验研究

3.1 实验平台介绍

如图8所示，实验平台为1个500 W的光伏并网系统，其中光伏并网系统包含主电路、控制电路和单相全桥逆变器3个独立的部分。控制电路主要包括数字处理器TMS320F28335、模拟信号调理电路、MPPT电路、保护电路、PWM脉冲生成电路及死区生成电路，主电路包含有Boost电路和输出滤波器以及电压电流检测传感器。

图8 实验平台实物Fig.8 Experiment platform

根据本文所提出的最大功率跟踪控制方法，设计出该方法的硬件电路，如图9所示。该硬件电路主要包括三角波发生电路、减法电路、比例积分电路、脉冲生成电路。经过调节后，用示波器测得三角波频率为9.92 kHz，幅值为7 V，PI调节器输出限幅在-5.7～5.7 V。Boost电路脉冲波形如图10 所示，图（a）中上下两个波形分别为Boost电路A和Boost电路B的脉冲波形，图（b）为脉冲波形上升沿放大图。通过调节R9使得PWMB的高电平时间比PWMA减少1 μs，即可控制ΔD始终为一恒定值，大约为0.01。

3.2 实验研究及结果

为了验证本文提出的方法的实用性，实验选用4块单晶硅光伏电池，每块光伏电池理想输出功率为 100 W，开路电压为 21.8 V，短路电流为 6.24 A，通过适当的搭配，分成最大功率点较为接近的两组，每组由2块光伏电池串联而成，每组理想最大输出功率约为 200 W。 实验中 ΔD=0.01，KP=0.01，KI=100。实验波形如图11～图12所示。

（1）如图11所示，图（a）和图（b）分别为本文提出MPPT方法稳定工作时的并网电流波形和输出功率波形，并网电流有效值为1.10 A，输出功率为241 W。图（c）和图（d）为扰动观察法稳定工作时的并网电流波形和输出功率波形，并网电流为1.03 A，输出功率为227 W。由图可以看出，2种方法在稳态时性能相近，功率波动都在15 W以内。

（2）图12中，图（a）和图（b）分别为施加阴影干扰时本文方法并网电流曲线和功率曲线，阴影干扰前后并网电流有效值从 1.24 A下降到 0.686 A，功率从272 W 下降到 151 W；图（c）和图（d）分别为施加阴影干扰时扰动观察法并网电流曲线和功率曲线，阴影干扰前后并网电流有效值从1.20 A下降到0.661 A，功率从 265 W 下降到 145 W。 对比图（b）和图（d）可以看出，本文提出方法有很好的动态性能，当外部环境变化时，能快速稳定的跟踪最大功率点。

图9 MPPT硬件电路原理Fig.9 Hardware circuit principle of MPPT

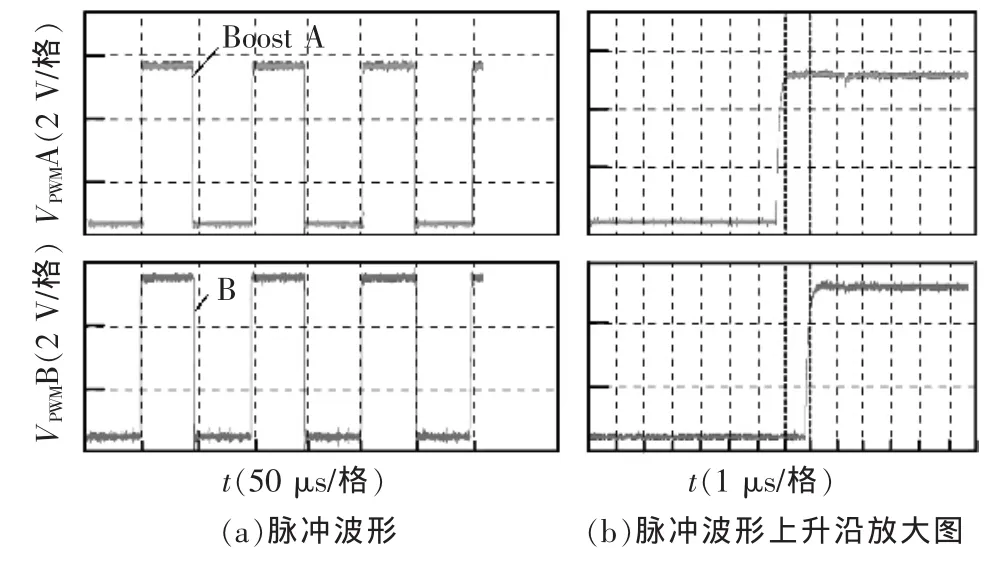
图10 Boost电路脉冲波形Fig.10 Pulse waveforms of Boost circuits

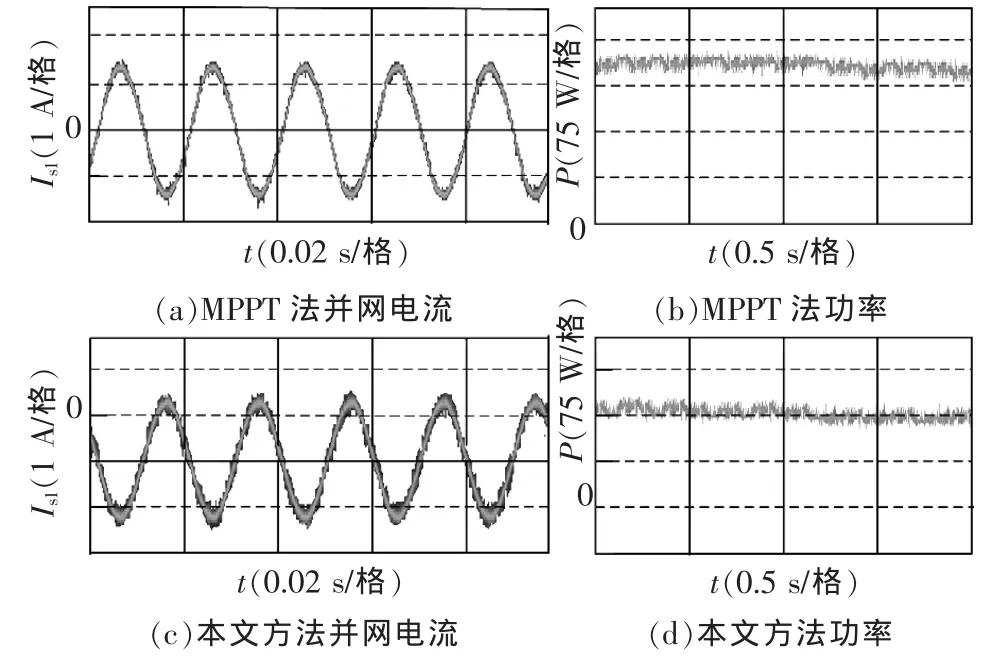
图11 稳定工作时的实验波形Fig.11 Experimental curves of steady-working state

图12 光照强度突变时的实验波形Fig.12 Experimental curves of insolation fluctuation

4 结语

本文根据大型光伏场中相邻光伏组件有相似的伏安特性曲线的特点，并基于扰动观察法的思想，提出了一种新的MPPT方法，该方法不用检测电流，只用检测电压，通过简单的硬件电路即可实现MPPT。仿真和实验的结果都表明，该方法能快速跟踪最大功率点，动态性能良好，同时具有较好的抗扰动能力。

［1］Chung H S H，Tse K K，Hui S Y R，et al.A novel maxi-mum power point tracking technique for solar panels using a SEPIC or Cuk converter［J］.IEEE Transactions on Power Electronics，2003，18（3）：717-724.

［2］Solodvnik E V，Liu Shengyi，Dougal RA.Power controller design for maximum power tracking in solar installations［J］.IEEE Transaction on Power Electronics，2004，19（5）：1295-1304.

［3］吴志鹏，卿湘运，杨富文，等.光伏发电系统的最大功率点跟踪算法及仿真研究［J］.电源学报，2013，11（4）：20-25.Wu Zhipeng，Qing Xiangyun，Yang Fuwen，et al.Manimum power point tracking algorithm and simulation of photovoltaic power generation system［J］.Journal of Power Supply，2013，11（4）： 20-25（in Chinese）.

［4］董密，杨建，彭可，等.光伏系统的零均值电导增量最大功率点跟踪控制［J］.中国电机工程学报，2010，30（20）：48-53.Dong Mi，Yang Jian，Peng Ke，et al.Zero average incremental conductance maximum power point tracking control for photovoltaic system［J］.Proceedings of the CSEE，2010，30（20）：48-53（in Chinese）.

［5］郑颖楠，王俊平，张霞.基于动态等效阻抗匹配的光伏发电最大功率点跟踪控制［J］.中国电机工程学报，2011，31（2）：111-118.Zheng Yingnan，Wang Junping，Zhang Xia.Maximum power point tracking control in the photovoltaic power generation based on dynamic equivalent impedance matching theory［J］.Proceedings of the CSEE，2011，31（2）：111-118（in Chinese）.

［6］周德佳，赵争鸣，袁立强，等.具有改进最大功率跟踪算法的光伏并网控制系统及其实现［J］.中国电机工程学报，2008，28（31）：94-100.Zhou Dejia，Zhao Zhengming，Yuan Liqiang，et al.Implementation of a photovoltaic grid-connected system based on improved maximum power point tracking［J］.Proceedings of the CSEE，2008，28（31）： 94-100（in Chinese）.

［7］张超，何湘宁.短路电流结合扰动观察法在光伏发电最大功率点跟踪控制中的应用［J］.中国电机工程学报，2006，26（20）：98-102.Zhang Chao，He Xiangning.Short-current combined with perturbation and observation maximum power point tracking method for photovoltaic power systems［J］.Proceedings of the CSEE，2006，26（20）：98-102（in Chinese）.

［8］车孝轩，崔容强.新的地域并网式太阳能发电系统的电力经济分析与设计［J］.太阳能学报，2005，26（2）：207-214.Che Xiaoxuan，Cui Rongqiang，The cost analysis and design of new grid-connected PV system in the community area［J］.Acta Energiae Solaris Sinica，2005，26（2）：207-214（in Chinese）.

［9］Mäki A.Power losses in long string and parrallel-connected short strings of series-connecter silicon-based photovoltaic modules due to partial shading conditions［J］.IEEE Transactions on Energy Conversation，2012，27（1）：173-183.

［10］Paraskevadaki E，Papathanassiou S.Evaluation of MPP voltage and power of mc-Si PV modules in partial shading conditions［J］.IEEE Transactions on Energy Conversation，2011，26（3）：923-932.

［11］lonso-Garcı＇aa M C C，Ruizb J M，Chenlo F.Experimental study of mismatch and shading effects in the I-V characteristic of a photovoltaic module［J］.Solar Energy Materials ＆ Solar Cells，2006，90（3）：329-340.

［12］田琦，赵争鸣，邓夷，等.光伏电池反向模型仿真分析及实验研究［J］.中国电机工程学报，2011，31（23）：121-128.Tian Qi，Zhao Zhengming，Deng Yi，et al.Simulation and experimental study about reverse model of photovoltaic cells［J］.Proceedings of the CSEE，2011，31（23）： 121-128（in Chinese）.

［13］Mei Qiang，Shan Mingwei，Liu Liying，et al.A novel improved variable step-size incremental-resistance MPPT method for PV systems［J］.Progress in Photovoltaics：Research and Applications，2003，11（1）：47-62.

［14］谢三军，荣飞，陈燕东，等.光伏电池不一致性检测及其应用［J］.中国电机工程学报，2012，32（19）： 24-29.Xie Sanjun，Rong Fei，Chen Yandong，et al.Inconsistency detection of photovoltaic cells and its applications［J］.Proceedings of the CSEE，2012，32（19）：24-29（in Chinese）.