双管正激电路数字控制系统设计方法的分析与对比

纪 婧 ，杜建华 ，王 均 ，马 皓

（1.浙江大学电气工程学院，杭州 310027；2.北京控制工程研究所，北京 100190）

引言

数字控制的双管正激电路以其开关管的电压应力小、可靠性高等优点而被广泛应用于中小功率的DC/DC电源［1-3］。针对其数字控制策略，已有大量的文献进行了研究［4-6］，但都有一定的局限性。文献［4］只利用数字重设计方法进行了数字补偿器的分析与设计；文献［5］提出可以利用z域的根轨迹进行数字系统的直接设计，但是并没有明确的给出具体z域根轨迹设计的方法。对于开关电源的数字控制，国内外主要研究集中在应用某种方法如z域根轨迹校正［6］来实现对数字控制器的设计。而对于各种数字控制器设计方法之间的对比研究少有涉及。但是只有明确各种方法的优缺点、适用范围和设计要点，才能在数字控制设计中根据实际情况选择合适的设计方法。

本文主要针对双管正激电路讨论3种数字控制器的设计方法：s域间接设计、ω域伪波特图设计和z域的根轨迹设计，分别用3种方法设计了系统补偿函数，并通过Matlab仿真验证补偿函数的准确性和设计方法的实用性，最后给出3种方法的设计要点和适用范围对比，对数字控制系统的设计有一定的指导意义。

1 双管正激电路的小信号模型

双管正激电路的拓扑如图1所示，它是一种带隔离变压器的Buck类变换器，所以其小信号模型与Buck电路的小信号模型十分类似。对此，国内外已经有学者做过相关工作，文献［7］给出了2个重要的传递函数。

图1 双管正激电路Fig.1 Switches forward converter circuit

（1）电路工作在连续工作模式（CCM）控制到输出的传递函数为

（2）电路工作在断续工作模式（DCM）控制到输出的传递函数为

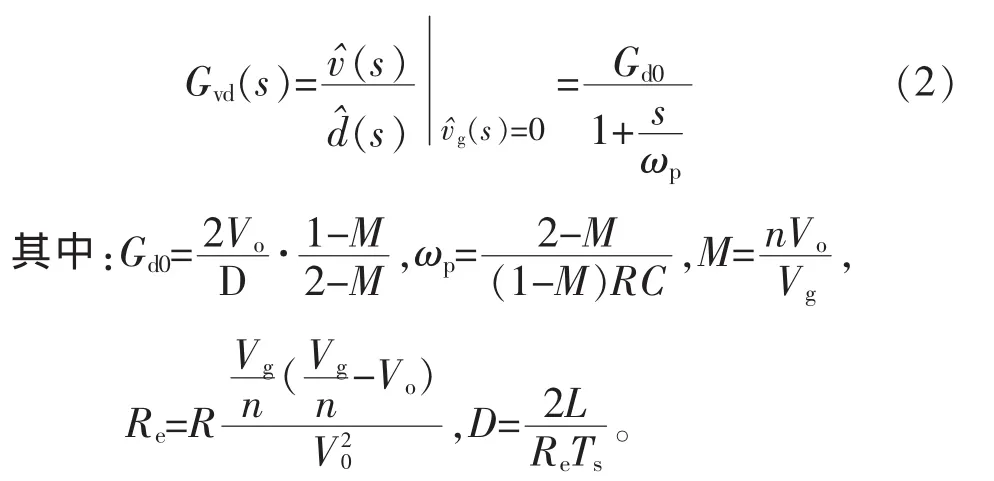
式中：Vg为输入电压；Vo为输出电压；n为变压器原副边比；L为电感；C为电容；R为输出电阻；M为电压增益；D 为占空比；Re为等效直流输入阻抗［7］。

2 数字控制系统的分析和设计

数字控制系统的设计是为控制器选择差分方程或等效频域传递函数的过程。在数字补偿器的设计中，通常采用2种方法：一种方法是在闭环回路中忽略任何零阶保持（ZOH）和采样，先在时域中初步设计，然后再通过某种近似技术变换为离散时间而得到一个离散时间补偿器；另一种方法是对连续时间被控对象通过零阶保持或其他方法并采样或利用某种近似方法变换为离散被控对象，得到被控对象的离散近似，然后再离散域中直接进行补偿器的设计［8］。

对于系统环路建模，考虑到主功率电路是在模拟域下工作的，而电压外环的控制是数字域下工作的。因此，建立了单电压环模式控制的数字双管正激环路模型的控制框图如图2所示。其中，Kd为采样分压电阻的分压比，Gc（z）为电压环补偿函数，Hd（z）表征DSP采样延时和输出误差延时，ZOH是数字处理与模拟电路之间的零阶保持器。对于DSP而言，ADC采样和DAC变换的比例。

图2 数字双管正激电路控制环路框图Fig.2 Control loop of digital switches forward converter circuit

本文采用电路的相关参数如表1，设计后的电路要求达到的技术指标如表2。

表1 本文使用到的基本变量参数Tab.1 Variable parameters in this paper

表2 本文设计系统技术指标Tab.1 Qualification in this paper

连续工作模式下的占空比［7］D为

随着负载的增加，电感电流会出现断续的状态，负载的临界值［7］Ro为

即 Ro≥14.6 Ω

2.1 s域间接设计

由以上的双管正激电路建模，式（1）给出电路的开环传递函数 Gvd（s）

采用电压单环控制，按照表2所要求的性能进行补偿网络的设计。用连续系统的设计理论确定补偿函数 Gc（s）［7］为

取Ro=15 Ω，由式（4）可知此时电路工作在断续工作模式，由式（2）可知此时的传递函数Gvd（s）为

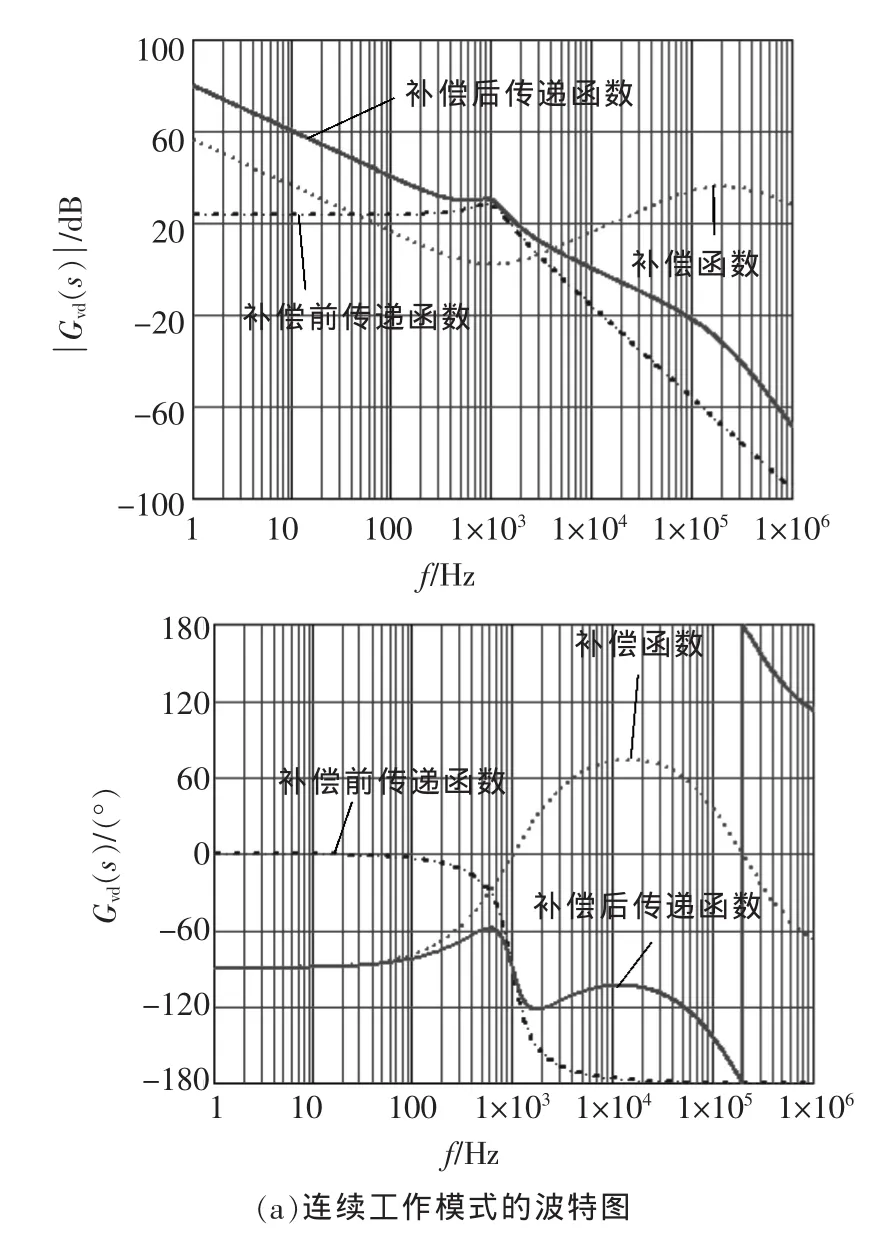
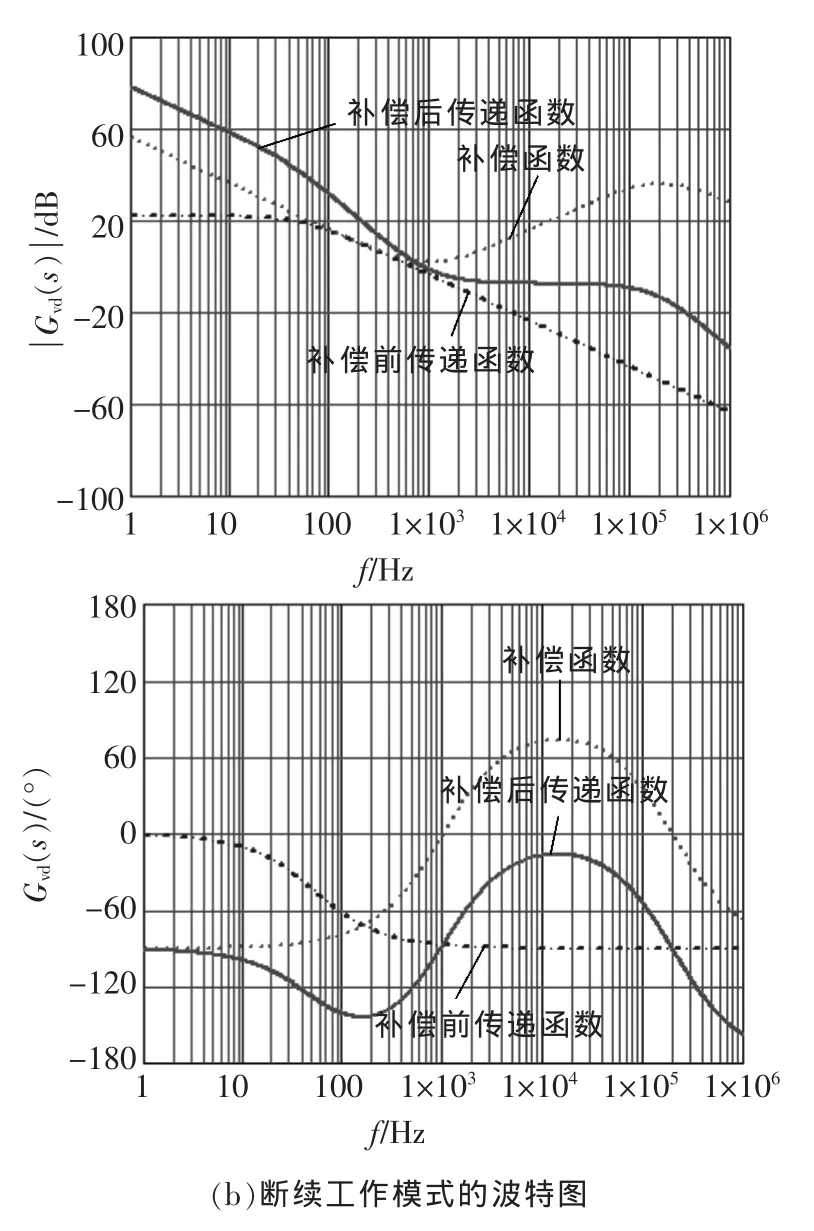
图3 连续域加入补偿函数的波特图Fig.3 Bode plots in s domain of the loop after compensation

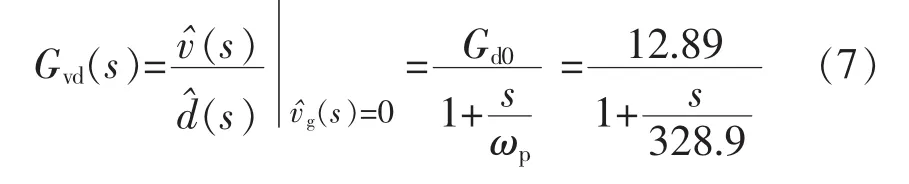
图3为在补偿网络如式（6）下，电路分别工作在连续工作模式和断续工作模式下的波特图。从图3（a）中可以看出经过补偿网络，在电路工作在连续工作模式下时，电路的相位裕度80°，幅值裕度30 dB，电路可以正常工作，具有很好的静态性能和动态性能；从图3（b）中可以看出如果此电路工作在断续模式，电路仍能正常工作，当输出电阻Ro＝15 Ω时，电路的相位裕度90°幅值裕度120 dB。

采用双线性变换公式［9］将连续系统数字化为

选取系统的采样周期 T＝1×10-5s，将 Gc（s）进行离散化，得到补偿函数的数字化形式，即

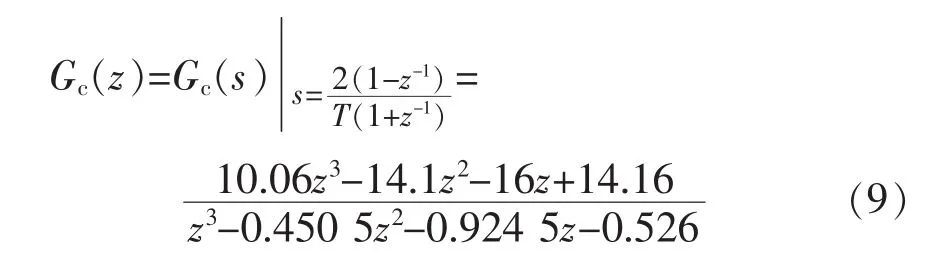
2.2 ω域波特图设计

利用式（8）将双管正激电路的传递函数Gvd（s）离散化为 Gvd（z），即

把 z=ejwT带入到 G（z）中可以得到 G（z）的频率响应。但z变换把s左半平面的主、次要带都映射到了z平面的单位圆内，所以涉及整个左半平面的常规频率响应法不适用于z平面。所以，采用ω变换［9］，即

将z域传递函数Gvd（z）变换为ω域的传递函数 Gvd（ω），即

虽然ω平面几何上类似s平面，但ω平面上的频率轴是畸变的。按照表2所要求的技术指标进行设计，由ω域和s域的对应关系，大致估计ω域下的截止频率［7］为原来s域假设截止频率10 kHz左右。则虚拟频率γ和实际频率ω的关系为

令 ω=jωw，得求出在 ω域下的波特图，用与连续系统相同的波特图校正法确定校正网络Gc（ω）。校正后系统的ω域开环传递函数为 Gs（ω）=Gc（ω）Gvd（ω）。可得补偿函数 Gc（ω）为

当该电路工作在断续工作模式，利用 式（8）和式（11），可以求出其在 ω域的传递函数 Gvd（ω），即

图4为采用如式（14）的补偿网络电路分别工作在连续工作模式和断续工作模式下的波特图。从图4（a）中可以看出，经过补偿网络，电路工作在连续工作模式时，该电路的相位裕度90°，幅值裕度40 dB，电路能很好地正常工作；从图4（b）中可以看出，对于在连续域下设计的补偿网络如果此时电路工作在断续工作模式，电路仍能正常工作，当输出电阻Ro＝60 Ω时，电路的相位裕度90°，幅值裕度60 dB。

利用式（11），将 Gc（ω）转换为数字域形式Gc（z），即

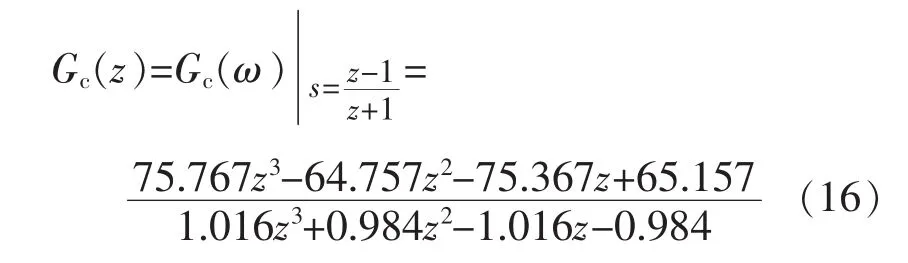
2.3 z域根轨迹设计

根据表2所要求的技术指标，大致确定z平面期望极点的允许范围［10］。由超调量的公式σ%=可得ξ=0.7；由调整时间的公式可得t≈可得 R≤e-TRe（s），即 R＜0.98；由峰值时间的公式，可得∠z=Tωd=9°，所以可大致确定补偿后函数的主导极点的范围。

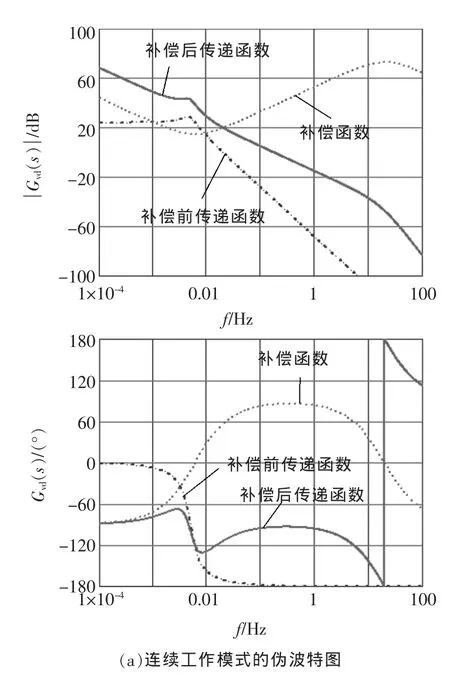
图4 加入补偿函数的ω域伪波特图Fig.4 ωfake Bode plots of the loop after compensation

因为原传递函数在 z域下的极点为 0.983±i0.044，所以应采用相位超前控制器［10］，来使得补偿后的极点位于期望的范围内，通过利用Matlab中SISO控制器设计［11］，用控制器的零极点对消控制对象不希望的零极点，从而使整个闭环系统具有满意的品质。使得补偿后的极点可以落在期待的位置附近，得到补偿前后的z域根轨迹如图5所示。得到的补偿函数为

此时选择的极点为-0.065 6±i0.174。

图5 补偿后的z域根轨迹Fig.5 Root locus in z domain of the loop after compensation

图5 为如式（17）所示的补偿网络，电路分别工作在连续工作模式和断续工作模式下的补偿前后的根轨迹。从图5（a）可以看出，电路工作在连续工作模式时补偿前根轨迹（实线）并没有落入期待中的区域，但是经过补偿函数后根轨迹可以经过期望区域，可以通过选择增益使得传递函数的极点落在期望的区域中。从图5（b）可以看出，电路工作在断续工作模式时的根轨迹同样存在经过期望区域中的根轨迹，这就说明在连续工作模式中设计的数字补偿函数对于断续工作模式同样适用。

3 MATLAB仿真分析

3.1 s域间接设计

在开关频率为100 kHz、不同采样频率情况下，数字域和模拟域的输出电压、电流对比如图6所示。从图6（a）中可以看出当采样频率接近或者高于开关频率时，模拟控制的输出与将模拟设计的补偿函数转换为数字控制的输出几乎相同；从图6（b）中可以看出当采样频率远低于开关频率时，模拟控制下设计的稳定的输出，转换到数字控制下会出现不稳定的现象。所以s域间接设计法适用于当采样频率接近或者高于开关频率的场合，模拟域的输出可以模拟数字与的输出，所以可以先在模拟域中设计补偿函数，再转换到数字域中。

图6 数字域和模拟域输出电压电流对比Fig.6 Output voltage and current in digital and analog design

3.2 ω域波特图设计

ω域波特图设计的输出电压、电流如图7所示。从图7中可以看出，通过ω域波特图设计的系统有较好的输出电压和电流特性，同时在满载切半载时也能有很好的动态相应性能。ω变换造成的频率轴畸变如图8所示。从图8可以看出，通过ω变换，使得伪波特图中的频率轴发生了畸变，与原始的频率成正切的关系。所以如果所要设计的剪切频率在附近时，会因为严重畸变造成设计上的困难和偏差；同时，因为要抑制开关纹波，所以在开关频率处会设置极点；因为频率轴畸变，所以此极点可以选在ωw=20左右。从图8中可以看出，此时ωw的变化对ωs影响不大。

图7 ω域波特图设计的输出电压电流Fig.7 Output voltage and current in ωfake bode design

图8 ω变换造成的频率轴畸变Fig.8 Frequency axis distortion for ωfake bode design

3.3 z域根轨迹设计

不同极点的输出电压、电流对比如图9所示。图中的极点均位于所要求区域，但是因为z域根轨迹设计的只考虑了超调量、峰值时间和调整时间等动态特性影响因素，并没有对静态误差和带宽的限制，所以设计时很可能出现系统拥有很好的动态相应性能，但是有一定的静态误差，如图9（b）。此时应该适当减小极点，增大零点，并且增大增益系数，牺牲一定的动态性能来保障系统的静态误差能在规定的范围内，做适当的调整可达到图9（a）。

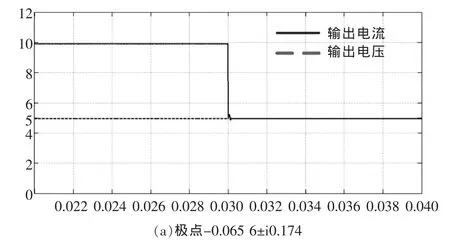
图9 不同极点的输出电压电流对比Fig.9 The output voltage and current in different pole

4 3种数字控制系统设计方法的对比

在相同的设计标准下，可以得出s域间接设计、ω域波特图设计和z域根轨迹设计3种设计方法，在进行数字系统设计时的优缺点、适用范围和注意事项。3种设计方法的对比大致如表3所示。

s域间接设计：因为忽略了零阶保持器等产生的延时，所以在转换到数字域中可能产生不稳定或者动态性能不好的现象，所以在设计过程中应保证较大的相位裕度大约60°左右较好。当采样频率低于开关频率时，转换到数字域中系统的性能可能和模拟域中电路的性能相差较大。所以s域间接设计的方法适用于采样频率高于开关频率的场合。

ω域波特图设计：因为ω平面上的频率轴是畸变的，不是线性的，这给设计带来了难度。所以在设计之前最好计算需要的截止频率所对应的在ω平面的值。同时因为频率轴是以的正切形式畸变的，当频率靠近，变化的越剧烈，越不利于设计的精确。所以ω域波特图设计适用于剪切频率远低于πfs的情况。

z域根轨迹设计：是因为z平面极点的密集程度很高，z平面上两个很接近的极点，对应的系统性能也会有较大的差别，同时因为在设计过程总并没有对静态误差进行限定，所以可能出现校正后的系统有较好的动态性能，但是有一定的静态误差。所以还需反复调整极点的位置，使电路达到期望的要求。但z平面根轨迹设计法和以上两种方法比起来是最直接的设计方法，它不需要通过任何转换，直接在z域上进行设计。当系统的静态特性较好，需要优化动态性能时，可以选择z域根轨迹法。

5 总结

本文建立了数字控制电压单环模式下双管正激电路的小信号模型。分析了3种不同的数字控制设计方法。s域间接设计比较方便，适合于采样频率高于开关频率的场合；ω域伪波特图设计由于频率轴发生畸变给设计带来了难度；z域根轨迹设计是最直接的设计方法，直接在离散域下设计，可以较好的优化系统的动态性能。通过对3种方法的对比和总结，为DC/DC变换器的数字控制系统设计提供了一定的参考。

表3 3种数字控制器设计方法的总结和对比Tab.3 The comparison of three digital design methods

［1］Tan F D.The forward converter：from the classic to the contemporary［A］.APEC 2002［C］.Dallas，USA，2002，2：857-863.

［2］陈威，吕征宇.新颖软开关谐振复位不对称双管正激变流器［J］.电源学报，2008，6（2）：88-94.Chen Wei，Lv Zhengyu.A novel soft switching asymmetrical dual switch forward converter based on resonant reset technique［J］.Journal of Power Supply，2008，6（2）：88-94（in Chinese）.

［3］王健，陈乾宏.1 kW磁集成双管正激变换器的研究［J］.电源学报，2007，5（4）：280-284.Wang Jian，Chen Qianhong.Design of 1 kW two transistors forward converter with integrated magnetics［J］.Journal of Power Supply，2007，5（4）：280-284（in Chinese）.

［4］黄博.60 W双管正激电源的数字与模拟控制研究［D］.杭州电子科技大学，2012：46-54.Huang Bo.The Research of Digital and Analog Control for 60W Switches Forward Power Supply［D］.Hangzhou Dianzi University.2012：46-54（in Chinese）.

［5］David R，Lopez F，Jose L.Analysis and design of a simple digital control algorithm for a phase-shift full-bridge DCDC power converter［J］.In Proc.12th Int.Power Electron.Congr.，2010：205-212.

［5］David R，Lopez F，Jose L.Analysis and design of a simple digital control algorithm for a phase-shift full-bridge DCDC power converter［J］.In Proc.12th Int.Power Electron.Congr.，2010：205-212.

［6］Guo L，Hung J Y，Nelms R M.Digital controller design for buck and boost converters using root locus techniques［J］.IEEE.IECON＇03.2003：1864-1869.

［7］徐德鸿.电力电子系统建模及控制［M］.北京：机械工程出版社，2005.

［8］Martin T W，Ang S S.digital control for switching converters［J］.In proc.IEEE-ISIE，1995：480-484.

［9］李文秀，赵乃真.数字控制系统［M］.哈尔滨：哈尔滨船舶工程学院出版社，1991.

［10］Katsuhiko ogata.Discrete-Time Control System［M］.China Machine Press：2004.

［11］John J D A，Constantine H H，Stuart N S.Linear Control System Analysis and Design with MATLAB［M］.Beijing China Machine Press：2008.