集成耦合电感的升压-反激变换器

王天兵，丁新平，王伯荣

（青岛理工大学自动化工程学院，青岛 266520）

引言

理论上，升压变换器（Boost converter）通过增加占空比可以实现较高电压增益［1］。但在实际应用中，升压变换器中等效串联电阻会造成电路的电压增益损耗和低效率。而且高电压输出时，开关管电压应力较大，输出二极管存在较严重的反向恢复问题，这也降低了变换器效率，所以设计出理想的具有高升压比和高效率的升压变换器有一定的难度［2］。反激变换器（Flyback）采用反激变压器可以实现较高电压增益，但由于绕组漏感在开关管上容易造成电压尖峰，增加开关损耗，降低变换器效率，所以反激变换器一般只应用于降压型中小功率场合［3］。而 Liang T.J和 Tseng K.C.提出了集成升压-反激变换器 IBFC（integrated boost-flyback converter）。该电路集成了反激变换器和升压变换器来实现电路的高升压比和高效率，取得了较好的效果［4］。该变换器要实现较高的电压增益，就需要增加占空比，但是占空比超过一定范围，变换器的效率会迅速下降。另外，变换器初级侧也会承受较高电流增益，造成开关管及二极管的电流应力增加，增加了电路的成本和复杂程度，因而集成升压-反激变换器的应用也受到了一定的限制。

为了克服上述电路的缺点，本文在集成升压-反激变换器的基础上，在Boost电路部分引入耦合电感提出了集成耦合电感的升压-反激变换器ICBFC（integrated coupled-inductor boost-flyback converter）。该电路优点明显：可以实现变换器电压增益的大范围拓展，避免了在实现较大电压增益时电路工作在极限占空比的状态；降低了开关管的电压应力，减小导通损耗和开关损耗；有效地抑制输出二极管的反向恢复电流，减小反向恢复损耗，提高功率器件的可靠性，具有一定的研究价值和应用潜力。

本文在分析集成升压-反激变换器的基础上，提出了集成耦合电感升压-反激变换器拓扑（ICBFC），详细分析了该电路在CCM（continuous current mode）模式下的工作原理，推导出了电路的电压增益、效率和寄生参数以及占空比的关系，最后通过仿真和实验验证了理论分析的正确性。

1 传统集成升压-反激变换器的分析

集成升压-反激变换器（IBFC）如图1所示，其通过集成升压电路（Boost）和反激电路（Flyback）来获得高电压增益［5］，其等效电路如图2所示。

由图2可以推导出，电路的电压增益Vo/Vi和效率η分别为

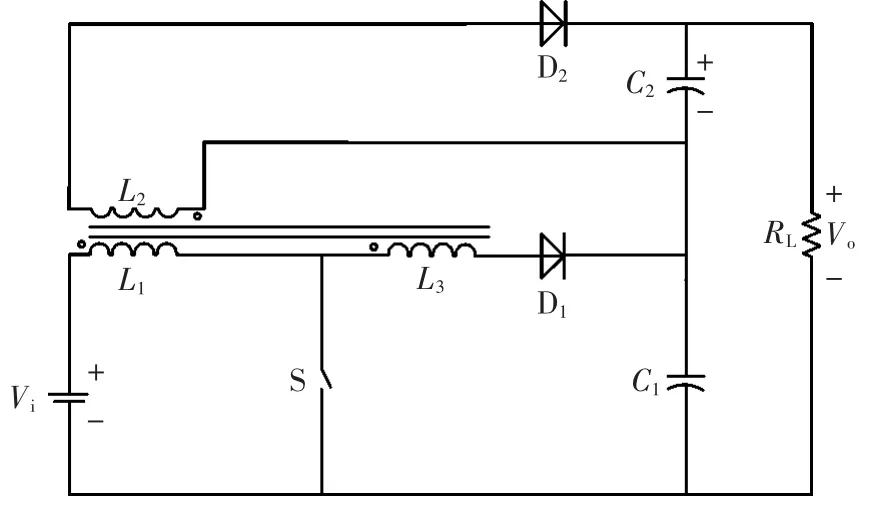
图1 集成耦合电感的升压-反激变换器Fig.1 Integrated coupled-inductor boost-flyback converter

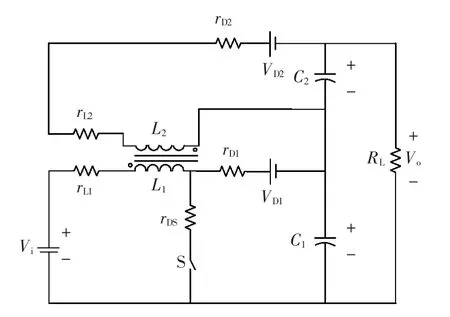
图2 集成升压－反激变换器等效电路Fig.2 Equivalent circuit of IBFC

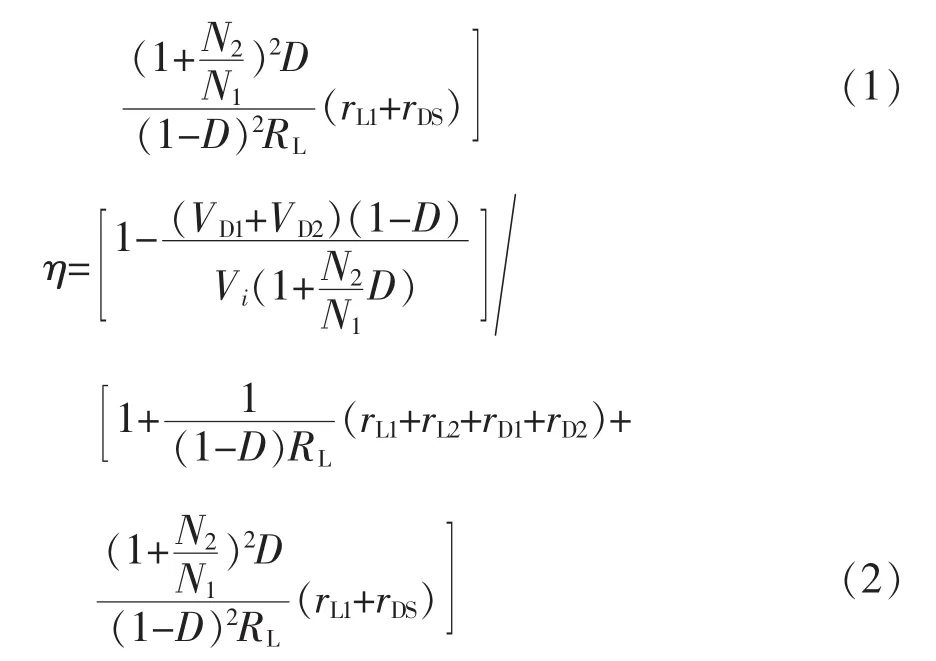
式中：Vi、Vo分别为电路的输入、输出电压；rDS为开关管导通电阻；D为开关管占空比；rL1、rL2分别为反激变换器原边、副边绕组寄生电阻；rD1、rD2分别为二极管 D1、D2的正向导通电阻；VD1、VD2分别为二极管D1、D2正向导通电压；N2/N1为反激变换器匝数比；RL为电路负载。

根据式（1）可以得出，在匝数比和寄生参数一定的情况下，随着占空比的增加该电路的电压增益先增加后减小，在占空比D=0.85时达到最大。但根据式（2）可以得到：在占空比 D＜0.5 时，变换器的效率保持在90%以上，占空比D＞0.5后效率却迅速下降。因此该电路较难同时获得较高电压增益和较高效率。而且在占空比也一定的情况下，变换器要实现较高电压增益，反激端电压增益会相应增加，这意味着初级侧和次级侧的电感量（包括漏感）比值将呈匝比的平方倍数增加，初级侧的电流将会增加，增加了开关管和二极管的电流应力。同时，反激端电压增益的增加将造成输出电容间电压的不平均分配，对输出滤波电容的容量及性能提出了较高要求，这样增加了变换器的成本和复杂程度，在一定程度上限制了该电路的应用［6］。

2 集成耦合电感升压-反激变换器

集成耦合电感的升压-反激变换器的电路拓扑结构如图3所示，该变换器主要由1个开关管S、2个快恢复二极管D1和D2、1个反激变压器及耦合电感、2个输出电容 C1和C2以及负载RL组成。

图3 集成耦合电感的升压－反激变换器Fig.3 Integrated coupled-inductor boost-flyback converter

2.1 工作模式分析

考虑反激变压器和耦合电感的漏感及数学模型后，集成耦合电感的升压-反激变换器的等效电路如图4所示。其中反激变压器匝数比为N2/N1，耦合电感匝数比为N3/N1，励磁电感为Lm，漏感为Lk1、Lk2、Lk3。

在CCM模式下，电路主要参数的波形如图5所示。

下面详细介绍以下4种工作模式：

模式 1（t0-t1）：t0时刻，开关 S 导通，D1、D2由于漏感的存在仍然导通。t1时刻，漏感Lk2、Lk3能量全部释放完，D1、D2反向偏置截止。

图4 集成耦合电感升压－反激变换器等效电路Fig.4 Equivalent circuit of ICBFC

图5 ICBFC电路在CCM状态下典型波形Fig.5 Typical waveforms of the ICBFC in CCM

模式 2（t1-t2）：在这个阶段，D1、D2反向偏置截止。输出电容C1、C2给负载RL供能。开关管S仍然导通。励磁电感电流im在t2时刻达到峰值。

模式 3（t2-t3）：t2时刻，开关管 S 开始关断，由于耦合电感的存在，D1开始导通，（开关管S开始关断，由于耦合电感的存在，D1开始导通）给电容C1充电。t3时刻，D2开始导通，给电容C2充电。

模式 4（t3-t0）：D1、D2导通后，电流 iD1给电容C1和负载RL供电，副边绕组电流iD2缓慢的给电容C2和负载RL供电。

2.2 稳态分析

为了简化分析，假设：（1） 输出电容 C1、C2足够大来保证输出电压VC1、VC2为定值，实现VO的稳定输出；（2）忽略漏感 Lk1、Lk2和 Lk3的作用； （3）忽略电容寄生参数的影响。设变换器匝数比n2=N2/N1，耦合电感匝数比n3=N3/N1。

图6给出了在CCM模式下开关管S导通和关断时电路的电流流向。

图6 开关周期内电路电流流向Fig.6 Current flow within one switching cycle

如图6（a），开关管S导通时，电源为反激变换器原边充电，形成回路Vi-L1-S。二极管D1、D2反向偏置，反激变换器及耦合电感处于储能阶段。同时，输出电容C1、C2给负载RL提供能量，形成回路C1-C2-RL。由此得出

式中：VL1为变压器原边电感L1两端电压；Iin、Io分别为电路的输入、输出电流；IC1（on）、IC2（on）为开关管导通阶段流过输出电容C1、C2电流；VC1、VC2为输出电容C1、C2两端电压。

如图6（b），开关管 S 关断，二极管 D1、D2导通，电源和原边电感L1、耦合电感L3共同为电容C1充电，形成回路Vi-L1-L3-D1-C1。同时副边电感L2给电容C2充电，形成回路L2-D2-C2。 而且电感L1、L2、L3为电容充电的同时也为负载RL提供能量，形成回路Vi-L1-L3-D1-L2-D2-RL。由此得到

式中：ID1、ID2为流过二极管 D1、D2电流； rL3为电感 L3的寄生电阻。

由式（10）可以推出

由式（4）、式（7）可知电容 C1在 CCM 稳态下的安秒平衡公式为

由式（5）、式（8）可知电容 C2在 CCM 稳态下的安秒平衡公式为

由式（12）、式（13）可以推出

由式（14）、式（15）可以看出，ID1和 ID2是相等的。

由式（3）、式（11）可以得出，在稳态下关于电感L1的伏秒平衡关系式为

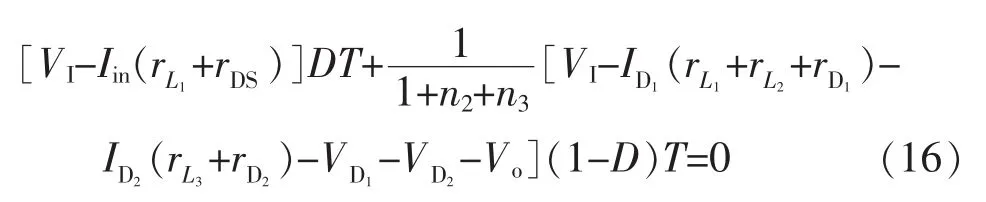
式中：D为电路占空比；T为开关管导通关断周期。

由式（16）可以得出

由式（17）可以看出变换器的电压增益与变压器匝数比、耦合电感匝数比、占空比及电路寄生参数有关。

在忽略寄生参数影响，占空比D=0.5的情况下，电路的理想电压增益为

由式（18）可知，在较低占空比下，耦合电感匝数的增加能够实现变换器较高电压增益。

由式（9）、式（14）和式（15）可以得到变换器的输入功率Pin和输出功率Pout分别为

式中：Pin、Pout分别为电路的输入功率和输出功率。

则转换器的效率η为

代入式（17）得

由式（21）可以得出，寄生电阻 rL1、rL2、rL3、rD1、rD2、rDS对变换器的效率造成了一定的影响。

3 仿真与实验结果

3.1 仿真结果

运用Saber仿真软件对集成耦合电感升压-反激变换器进行了仿真，仿真参数如表1所示。

表1 系统额定工作参数Tab.1 System rated parameters

图7～图9为考虑部分寄生参数，用Saber软件实现的闭环电路仿真波形。其中图7为输入电压Vi=5 V时输入电流im和输出电压Vo的仿真波形。由图7可以看到输入电流im处于CCM模式，输出电压Vo稳定在50 V。图8为输入电压Vi=5 V时电路输出电压仿真波形。仿真电路实现了50 V的稳定输出，电容C1和电容C2两端电压分别为30 V和20 V。图9为输入电压Vi=5 V时流过二极管D1和D2电流的仿真波形，这与图5所示的电路波形相吻合。

图7 Vgs，Vi，im，Vo的仿真结果Fig.7 Simulation results of Vgs，Vi，imand Vo

图8 输出电压仿真Fig.8 Simulation results of output voltage

3.2 实验结果

本文搭建了1台30 W的实验样机来验证该电路的实用性，样机如图10所示。样机使用STM32F103RBT6作为控制芯片，其输出的PWM控制信号通过光耦芯片TLP250来驱动开关管S的通断，开关管S采用MOSFET芯片CSD17505，整流二极管采用肖特基二极管SR560，输出电容采用470 μF电解电容。

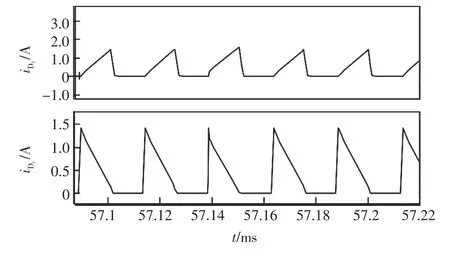
图9 电流iD1、iD2的仿真结果Fig.9 Simulation results of current iD1 and iD2

图10 实验样机Fig.10 Experimental prototype

实验中样机参数与仿真基本一致，唯一不同的是实际电路中寄生参数带来的EMI影响较大，测得的数据有些许偏差。图11～图14为样机实验得到的结果。其中图11为电路的效率曲线，随着负载的增加，电路的效率先增加后减小，这与式（22）的计算结果相近。图12为输入电压Vi=5 V时，输入电流im和输出电压Vo的实验波形，这与图7的仿真波形较匹配。图13为电路输出电压实验波形，电路实现了50 V的稳定输出，电容C1和C2两端电压分别为30.6 V和19.3 V。实验结果与图8的仿真结果相一致，证明了闭环控制的有效性。图14为输入电压Vi=5 V时，流过二极管D1和D2电流的实验波形，这与图9的仿真波形大致吻合。

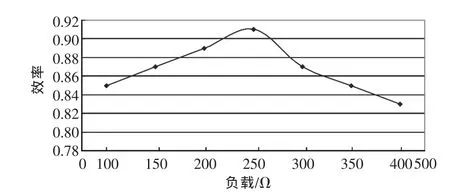
图11 效率曲线Fig.11 Efficiency curve

图12 Vgs，Vi，im，Vo的实验波形Fig.12 Experimental waveforms of Vgs，Vi，imand Vo

图13 输出电压实验波形Fig.13 Experimental waveforms of output voltage

图14 电流iD1，iD2的实验波形Fig.14 Experimental waveforms of current iD1 and iD2

4 结论

本文提出了一种高升压比高效率DC-DC变换器—集成耦合电感升压-反激变换器。通过分析电路在CCM模式下的工作原理推导出了电路电压增益、效率和寄生参数以及占空比的关系。该电路的主要优点如下：

（1）耦合电感通过分担反激端的电压增益进而实现了变换器的高电压增益和高效率；

（2）耦合电感降低了开关管和二极管的电压电流应力，简化了电路器件选型，增强了电路实用性。

仿真和实验结果验证了本文中理论分析的正确性。

［1］沈健，刘鸿鹏，王卫.高升压比DC-DC变换器的研究［J］.电源学报，2014，12（5）：1-6.Shen Jian，Liu Hongpeng，Wang Wei.Research on high Step-up ratio DC-DC converter［J］.Journal of Power Supply，2014， 12（5）：1-6（in Chinese）.

［2］罗全明，闫欢，孙明坤，等.基于拓扑组合的高增益Boost变换器［J］.电工技术学报，2012，27（6）：96-102.Luo Quanming，Yan Huan，Sun Mingkun，et al.High stepup boost converter based on topology combination［J］.Transactions of China electrotechnical society，2012，27（6）：96-102（in Chinese）.

［3］王兆安，刘进军.电力电子技术［M］.5版.北京：机械工业出版社，2009.

［4］T J Liang and K C Tseng.Analysis of integrated boost-flyback step-up converter［J］.IEEE Trans.IEE Proc.-Electr.Power Appl，2005，152（2）：217-225.

［5］K C Tseng and T J Liang.Novel high-efficiency step-up converter ［J］.IEEE Trans.IEE Proc.-Electr.Power Appl，2004，151（2）：182-190.

［6］Wai Rongjong，Duan Rouyong.High step-up converter with coupled-Inductor［J］.IEEE Trans.IEE Proc.-Electr，2005，20（5）：1025-1035.