混沌优化反馈校正串级控制
李青芮 李 平 张 鹏
(1. 西北工业大学自动化学院,西安 710072;2.辽宁石油化工大学信息与控制工程学院,辽宁 抚顺 113001)
在复杂工业过程控制中,串级控制系统利用率非常高,因此建立一个较好的串级控制系统十分重要。串级控制系统具有改善过程的动态特性、提高系统控制质量、迅速克服进入副回路的二次扰动、提高系统工作频率及对负荷变化的适应性较强等特点。串级控制方法成功使用在液压仿真转台和cvT速比控制系统中[1,2],但是其算法非常复杂,不容易操作。专家PID的控制方法成功应用在主汽温控制系统中[3~5],但此方法参数的选取极其复杂。
笔者提出一种基于混沌优化的反馈校正控制方法,首先通过混沌映射的方法对副回路进行数学辨识,得到其传递函数后依据辨识出的数学模型进行离线PID参数优化,确定副回路控制器后,对整个被控对象进行传递函数辨识,最后依据被辨识出的传递函数构造控制器对被控对象进行控制。以某主汽温控制系统为被控对象进行仿真研究,仿真结果表明该方法具有较好的控制效果。该方法的优点在于一切参数自动优化,鲁棒性能高,可以承受模型时间常数±25%和增益±40%的变化而不失去控制能力。
1 控制方法基本原理①
1.1 混沌映射
生态学中的虫口模型(即Logistic映射)如下:
Xn+1=uXn(1-Xn),n=1,2,3,…
(1)
其中Xn∈(0,1)。当u=4时,将发生混沌映射,只要n取一定的数值,Xn会遍历0~1之间的几乎每一个值。利用此性质就可以将任意一个变量映射到一定的域内,遍历此域内的每一个值从而进行全局搜索[6]。
1.2 系统反馈校正方法
控制器的设计基于被控对象的数学模型,首先假设被控对象的开环传递函数为:

(2)
其中K是系统增益,Tn是系统时间常数。
将所期望的系统闭环传递函数规定为如下形式:
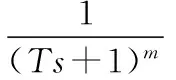
(3)
其中T为可调参数,随着T变大,闭环响应速度变慢;T变小,闭环响应速度变快。因此,控制器的传递函数可由下式来表示:
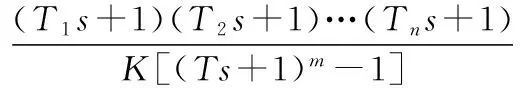
(4)
控制器的输入输出关系为:
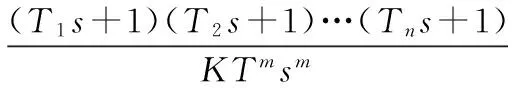
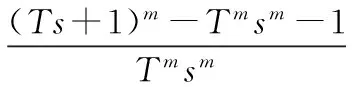
(5)
其中e(s)是系统反馈与目标值的误差。
根据式(5)构造控制器。
1.3 控制器参数优化方法
控制器参数优化分为4步:
a. 利用混沌映射对系统副回路进行数学辨识,流程如图1a所示;
b. 利用混沌映射对系统副回路PID控制器参数进行整定,流程如图1b所示;
c. 将步骤b得到的PID参数代入模型,利用步骤a的方法辨识整个被控对象的传递函数;
d. 采用系统校正方法设计控制器对被控对象进行控制。

图1 控制器参数优化相关流程
2 仿真研究
对某主汽温控制系统进行仿真研究[7],其内环传递函数为:

(6)
外环传递函数为:
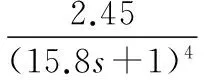
(7)
2.1 内环模型混沌识别
首先对内环系统的阶跃响应曲线进行模型识别,得到的曲线如图2所示,图中两根曲线的相似度极高,其中实线为目标曲线,虚线为辨识得到的曲线,得到模型传递函数如下:
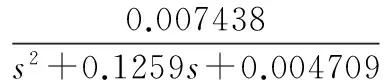
(8)

图2 内环模型的阶跃响应曲线与辨识曲线
2.2 PID参数优化
对得到的W2(s)传递函数进行PID控制,并对其参数进行优化,设置其目标闭环传递函数如下:

(9)
优化后得到的辨识曲线与目标曲线如图3所示。

图3 内环PID目标曲线与辨识曲线
优化得到的PID参数为:P=227.8,I=4.2652,D=35.432。
2.3 识别整体模型
对内环采用上述参数的模型进行整体识别,结果如图4所示。在图4中阶跃响应曲线与辨识曲线重叠,说明相似度极高。
识别出来的模型为:

(10)

图4 被控对象阶跃响应曲线与辨识曲线
2.4 控制系统抗干扰能力研究
根据2.3节中辨识出的模型所设计的控制器如图5所示。

图5 系统反馈校正控制器
识别出来的模型为:
其中,A=0.46326,B=0.083566,C=0.0072849,D=0.00030375,E=0.0000047706,K=0.000011688,T=10。
T为可调参数,A、B、C、D、E为识别出来的系统参数(同1.2节中的Tn,n=1,2,3,4,5)。使用此控制器对系统进行仿真,得到的系统阶跃响应曲线如图6所示,在100s时系统达到稳定没有超调。在串级控制系统中,内扰对系统的影响并不是很大,对系统的品质基本不会造成不良影响,同时系统还具有很好的抗外干扰的能力。为了验证系统对外部干扰的适应能力,在系统输出稳定后200s时,对系统输出加入20%的扰动,系统的响应如图6所示,从曲线可以看出系统的抗外部干扰能力非常强,大约在270s就恢复正常。

图6 系统阶跃响应及其抗干扰响应
2.5 对象参数变化下控制系统的鲁棒性
随着季节、天气、工作负荷和工况的变化,被控对象的时间常数和增益都在变化,因此一个具有强鲁棒性的控制器非常必要。
为检验控制器的鲁棒性,分别对系统的时间常数和增益进行改变,然后观察系统的适应能力。首先调节对象增益K,由2.45变化到1.45和3.45,控制系统的动态响应曲线如图7a所示。K值增大时,系统响应变快,超调量增大;K值减小时,系统响应速度变慢。此次系统增益改变分别达到±40%,表明系统对增益变化的鲁棒性较好。
当对象时间常数T由15.8变化到11.8和19.8时,控制系统的动态响应曲线如图7b所示。T值增大时,系统超调增大,反应时间变长;T值减小时,系统在上升过程中伴有小幅振荡。系统时间常数改变分别达到±25%,表明系统对时间常数改变的鲁棒性非常好。


图7 系统响应曲线
从仿真结果可以看出,基于混沌优化的反馈校正串级控制系统具有较强的鲁棒性,特别是对对象增益的变化具有很强的鲁棒性。
3 结束语
针对有明显滞后的工业系统,提出混沌优化反馈校正方法,给出了控制器结构和控制器参数优化方法。该方法控制结构简单、可调参数少,而且参数有物理意义,便于参数的整定。通过仿真,表明控制器具有良好的跟踪性能和抗干扰性能,鲁棒稳定性能也较好,具有实际应用意义。
[1] 郭敬,赵克定,郭治富.液压仿真转台的PFC-PID串级控制[J].航空学报,2008,29(5):1395~1400.
[2] 刘金刚,周云山,邹乃威,等.DMC-PID串级控制在cvT速比控制系统中的应用[J].湖南大学学报(自然科学版),2007,34(7):44~48.
[3] 王志萍,彭道刚,杨平,等.专家PID控制在主汽温控制系统中的应用[J].现代电力,2004,21(4):58~61.
[4] Yin C Q,Hui H Z.Cascade Control Based on Minimum Sensitivity in Outer Loop for Processes with Time Delay[J].Journal of Central South University,2012,(9):2689~2696.
[5] Duan H D,Tian Y T,Yang M.Cascade Control with Low Order Active Disturbance Rejection Controller for Higher Order Nonlinear Cascade System[C].Proceedings of 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems.Shanghai:IEEE,2009,(2):241~245.
[6] 侯威,封国林,董文杰.基于复杂度分析logistic映射和Lorenz模型的研究[J].物理学报,2005,54(8):3940~3945.
[7] 王国玉,韩璞,王东风,等.PFC-PID串级控制在主汽温控制系统中的应用研究[J].中国电机工程学报,2002,22(12):50~55.

