单神经元PID控制算法在智能车控制系统的应用

侯一民 朱志超

(东北电力大学自动化工程学院,吉林 吉林 132000)

智能车即无人驾驶车辆，涉及环境感知、路径规划、驾驶行为智能决策、车辆导航定位及车辆自动控制等技术领域，作为智能交通系统中许多高新技术的载体而受到广泛关注。对于智能车的研究，控制部分作为最底层和最重要的环节，是智能车的核心部分[1]。

PID算法作为典型的传统反馈控制，以结构简单、鲁棒性好及稳定性高等优点而广泛应用。肖建文和李永科运用增量型PID控制算法对舵机和电机进行控制，但在环境变化时，该算法不能及时自整定控制参数，小车的行驶易受干扰而出现振荡[2]。针对这一缺点，林焕新等提出了模糊PID控制算法，该方法克服了PID参数不能自整定的缺点，但模糊控制规则是根据研究者的先验知识和实践经验确定的，具有不完整和主观性强的缺点[3]。黄志强提出了分段PID控制算法，该算法需对路径进行分段，降低了控制器的运行速度，从而影响小车的行驶速度[4]。为此，笔者尝试将具有自学习、鲁棒性强及不需建立具体的数学模型等优点的单神经元算法与经典PID算法相结合实现对智能车的控制。

1 智能车硬件结构①

智能车能否平稳快速行驶，取决于小车系统的路径识别、判断及反应能力等，这都与小车的硬件系统有关，因此设计时要充分考虑其合理性。智能车硬件整体结构如图1所示。

图1 智能车硬件整体结构框图

由寿命长、污染小的额定电压为7.2V的镍镉充电电池为智能车各系统提供特定电源，以MK60DN512ZALQ10单片机为控制核心[5]，经线阵CCD镜头采集的赛道信息成像在感光元件上，量化后得到128个电压值，经运算放大器传给单片机的A/D转换器，并进行图像处理，将结果传给控制器，输出结果：

a. 经单片机FTM模块产生方波，传给BTN7960模块，根据输入的占空比控制输出电压，进而控制电机转速，最终的控制目的是使智能车以最快的速度沿赛道中心线稳定运行；

b. 单片机FTMPW模块产生PWM方波，方波的脉宽决定了舵机的输出转角，用于控制车轮沿赛道中心线行驶，最终的控制目的是使智能车能够做半圆周运动，即驶过弯道。

2 智能车的运动学模型

智能车在直道行驶时，经BTN7960芯片输出的电压与电机转速成正比，因此只需对舵机建立运动学模型。智能车的舵机安装在前轴中心处，所以舵机驱动角度与前轮转向角度成正比关系，因此只需证明智能车在转弯时是圆周运动，控制器即可实现对舵机的转弯控制[6]。智能车舵机运动力学分析如图2所示，智能车从M点出发以速率vA行驶t时刻后走过弧长S到达N点，vD为车前轮转过一定角度后的行驶速率；O′为瞬时转向中心。

图2 智能车舵机运动力学分析

由图2可知，智能车运行弧长S对应的半径R为：

(1)

式中L——车前轮与后轮间的距离；

β——前轮行驶方向偏离轴中心线的角度。

角度ψ对时间的积分公式为：

(2)

其中，vA为车后轮行驶速率；ψ为车后轮行驶方向偏离国际坐标轴x轴的角度。

图2中令M点坐标为(xM，yM)，将其对时间进行积分可得：

(3)

(4)

将式(2)代入式(3)、(4)并对其进行积分，可得：

(5)

(6)

化简消掉ψ可得：

(7)

式(7)中，a、b和L均为常数，因此其结果只与β有关，当β确定时，M点的运行轨迹为圆。所以可以确定智能车在转弯过程中做的是圆周运动，继而可以应用控制器对智能车的舵机在弯道中进行控制。笔者引入单神经元PID控制器实现对智能车舵机的控制。

3 智能车控制策略

对于智能车控制系统，若把跑道的路径变化看作系统的输入，那么此系统可以看作一个随动系统，智能车应跟随道路变化而运行；若把跑道的路径变化看作对智能车控制系统的扰动，那么此系统可看作一个恒值控制系统，智能车应能够适应道路曲变而更加平稳快速地运行。因此要选择合适的控制算法，既要满足跟随系统的动态特性，又要满足恒值控制系统的稳定性。

运行中，智能车的行驶环境会受光照等因素影响，针对电机和舵机的控制，应能实时准确地跟踪多变的赛道。

采用传统PID控制算法时，智能车的行驶方向和道路中心线之间的距离偏差，经过PID控制器的积分和微分环节处理后，分别计算出积分值和微分值，再将积分值、微分值和偏差按一定的线性规律组合，在比例环节作用下得到实际输出，由于CCD传感器是按一定周期获取道路信息的，因此必须将连续的PID控制算法离散化，得到增量型PID算法：

(8)

3个系数在控制过程中分别起着重要的作用，因此对3个系数的在线实时整定非常必要。经典PID本身不具备参数自整定功能，很难控制智能车实时适应环境变化。

在此，笔者将鲁棒性强的经典PID算法与自适应能力强的单神经元算法相结合，实现对智能车系统的控制。神经元网络是智能控制的重要组成部分，是本质性的非线性系统。单神经元作为构成神经网络的基本单位，具有自学习和自适应能力，且结构简单易于计算，将其与PID算法相结合，通过修改神经元的权值系数ωi(t)实现其性能。也可以在一定程度上解决传统PID调节器不宜在线实时整定参数，难以对一些过程复杂、参数时变、非线性和强耦合系统进行有效控制的不足。

3.1 单神经元数学模型

单神经元的结构示意如图3所示。

图3 神经元数学模型结构

神经元的数学模型[7]如下：

(9)

式中u——神经元外部状态输出值；

xi(t)——t时刻单神经元的外部状态输入信号，即t时刻智能车的行驶方向和道路中心线间的距离偏差；

ωi(t)——t时刻神经元外部输入信号xi(t)的权值系数；

θ——神经元状态阈值。

3.2 单神经元PID控制器

单神经元PID控制器的结构框图[8]如图4所示。

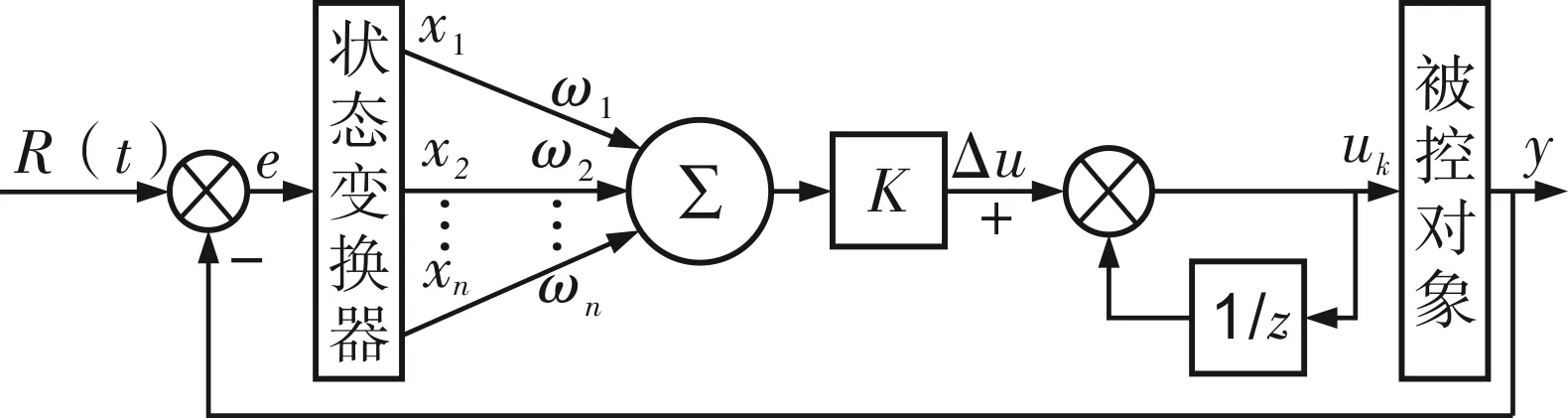
图4 单神经元PID控制器结构

取n=3、θ=0，则单神经元PID的外部状态输入即t、t-1和t-2时刻智能车的行驶方向和道路中心线间的距离偏差分别为：

x1(t)=R(t)-y=e(t)

(10)

x2(t)=e(t)-e(t-1)

(11)

x3(t)=e(t)-2e(t-1)+e(t-2)

(12)

单神经元PID的状态输出为：

(13)

由式(11)～(13)知，式(14)～(16)具有按偏差的比例、积分和微分输入项，故ωi(t)可以看作是增量式PID的比例、积分和微分系数：

ω1(t)=ω1(t-1)+ηiz(t)u(t)x1(t)

(14)

ω2(t)=ω2(t-1)+ηpz(t)u(t)x2(t)

(15)

ω3(t)=ω3(t-1)+ηdz(t)u(t)x3(t)

(16)

其中，K为神经元比例系数，K的大小决定系统的快速性，但过大会使系统的超调量加大引起系统不稳定，过小会使快速性变差，因此K值的选取要适中；ηp、ηi、ηd分别为比例、积分和微分学习速率；z(t)为性能指标或神经元递推信号，z(t)=e(t)。

3.3 单神经元PID控制器的参数整定

对于学习速率ηp、ηi和ηd的整定，可先取较小值。如果此时过程从超调趋向平稳的时间偏长，可适当地增加ηp和ηd；反之则减小。如果响应特性出现上升时间短、超调过大的现象，应减小ηp；反之增大。权值系数ωi(t)的整定，采用有监督的Hebb学习规则[9]，学习规则又是通过计算算法来实现的。

有监督的Hebb学习规则如下：

a. 选定权值系数ωi(t)的初值为ωi(0)；

b. 由式(14)～(16)求得xi(t)；

d. 计算y；

e. 调整ωi(t)，若实际输出与设定值相符，ωi(t)稳定不变；否则返回步骤b，直到ωi(t)达到设定值。

有监督的Hebb学习算法如下：

(17)

(18)

ωi(t)=ωi(t-1)+ηie(t)u(t)xi(t)

(19)

4 仿真与结果分析

4.1 Matlab仿真结果对比

对于单神经元PID控制算法，不需要建立受控对象的精确数学模型，可由系统偏差来调整控制量，从而使系统达到期望输出，对于PID和模糊PID控制算法所建立的传递函数[10]为：

(20)

取舵机的周期为0.200ms，经测试，智能车的单片机FTMPW模块产生PWM方波的脉宽为0.005～0.025ms,对应舵机的输出转角为0～180°，将舵机左打死即将车轮摆正，可求得舵机偏差约为640份。又因线阵CCD感光元件是一条由128个点构成的直线，因此图像的最大偏差为128份，控制器中的比例系数P可近似由下式求取：

(21)

采用试凑法分别求取Ki=3.0、Kd=0.0001。

采用PID、模糊PID和单神经元PID 3种控制算法的输出响应曲线对比如图5所示。

图5 3种控制算法的输出响应曲线对比

3条响应曲线的性能指标比较见表1，Tp为系统的响应速度；Ts为系统达到给定值的所需时间；超调量σ反映了调整过程中系统输出最大值与稳态值的偏差；振荡次数N反映了响应曲线在调节时间范围内围绕稳态值振荡的次数。稳态误差ess是反映系统准确性的性能指标，当时间趋于无穷大时，系统响应的期望值与实际值之差。

表1 3条响应曲线的性能指标比较

综上所述，采用单神经元PID控制算法对智能车进行控制，在稳定性、准确性和快速性方面都取得了较好的控制效果。

4.2 实测数据对比

分别用PID、模糊PID和单神经元PID 3种控制算法对智能车的舵机和电机进行控制，使其分别在相同环境的30m带有不同弯道和直道、4m弯道和10m长直道中进行3次运行试验，表2为所用时间与速度的对比。

表2 智能车在3种跑道上所用时间与速度的对比

从表2数据中可以看出：智能车在带有不同弯道和直道的30m长赛道自主行驶时，采用单神经元PID控制算法时的平均用时最短，平均速度最快；在同弯度的4m长弯道中自主行驶，采用单神经元PID控制算法时的平均用时最短，平均速度最大；在10m长直道中自主行驶，采用单神经元PID控制算法时的平均用时最短，平均速度最大。证实了智能车在同等条件的赛道中自主运行，采用单神经元PID控制算法对智能车的电机和舵机进行控制，行驶速度最快、所用时间最短，能达到更好的控制效果。

5 结束语

笔者提出了应用单神经元PID控制算法对智能车进行控制，根据PID、模糊PID和单神经元PID 3种控制算法的Matlab仿真结果，以及分别应用于实际智能车控制实验中的实测数据比较可知：由于单神经元PID控制算法的自学习自适应能力强，将其应用在智能车的舵机和电机控制后，智能车的运行速度更快、鲁棒性更强、效果更好。

[1] 赵盼.城市环境下无人驾驶车辆运动控制方法的研究[D].合肥:中国科学技术大学,2012.

[2] 肖文健,李永科.基于增量式PID控制算法的智能车设计[J].信息技术,2012,(10):125～127.

[3] 林焕新,胡跃明,陈安.基于自适应模糊控制的智能车控制系统研究[J].计算机测量与控制,2011,19(1):78～80.

[4] 黄志强.基于CCD摄像头智能车分段PID控制算法设计[J].电子设计工程,2011,19(2):55～57.

[5] 卓晴,黄开胜,邵贝贝,等.学做智能车——挑战“飞思卡尔”杯[M].北京:北京航空航天大学出版社,2007:128.

[6] Liu Q Q,Wang B,Ma X W.The Research of Intelligent Vehicle’s Steering Control System Based on Fuzzy Control[C]. Advanced Computational Intelligence(ICACI).Nanjing:IEEE,2012:474～478.

[7] 王振臣,赵莎,杨康.汽车主动悬架单神经元PID控制器设计[J].机械设计与制造,2013,(11):29～32.

[8] 任俊杰.基于PLC的单神经元PID控制器的设计与实现[J].制造业自动化,2012,34(7):11～13.

[9] Zhang C N,Zhao M,Wang M.Single Neuron Rational Model of Arithmetic and Logic Operations[J].IEEE Transactions on Neural Networks,2011,3(11):739～747.

[10] 严大考,李猛,邹栋,等.基于MC9S12XS128单片机的智能车控制系统的设计[J].华北水利水电学院学报,2013,34(1):106～110.