巧用“画图策略”打破小学数学“瓶颈”问题
马健

一、创设画图教学情境,增强学生画图解题意识
对于画图策略的应用需要创建画图教学情境。通过画图解答问题,培养学生思维习惯及探究能力。但在实际教学过程中,大多数学生由于受到各种因素的共同影响,使得学生失去了学习数学的兴趣,以至于见到数学问题,出现畏惧心理,甚至逃避。因此,这就需要教师深入理解数学内涵,掌握数学学科的自身特点及小学生的自身发展规律,采用鼓励性话语,创设画图情境,激励学生采用画图策略解决数学问题,让学生意识到画图策略在解题中的重要性,逐渐增强画图解题意识。
如:在三年级上册教材中,有这样一道思考题:“若想铺满长2000米的石子路,一位工人第一天铺了500米,第二天铺了600米,还有多少米没有铺完呢?”学生初次拿到该题目时,由于文字叙述较少,学生难以理解。在解题过程中,教师就可利用画图策略将本题意思形象地表现出来(如图1所示)。根据图1学生能够理解题目思路,并可直观地看到第一段线段表示第一天铺了500米,第二段线段表示第二天铺了600米,那第三条线段就表示没有铺的。学生一目了然,能够快速地解答出正确答案。
[500 600 ?]
图1
二、重视画图过程指导,提高学生画图解题水平
小学生的思维能力还没有形成,需要教师在画图策略中加以指导。画图解题是一个循序渐进的过程,需要良好的思维分析能力,从中寻找正确的画图方法,同时掌握正确的画图思想,能够客观分析题意,找出题目中各个数量间的关系,进而提高画图解题水平。在解题过程中还应注意学生思维能力的发展情况,教师应根据学生的不同层次来制定不同的教学环境及教学目标,真正实现“因生施教”的教学模式。尤其对于低年级的学生,教师可放低画图的要求,仅仅让学生能够看懂图中呈现的意思,并能够清楚地表达出题目意思及找清数量之间的关系即可,耐心引导学生画图。
如:学习完“长方形面积计算方法”内容后,教师可根据学生实际情况,列举下题。
已知长方形的周长为48米,若在宽及长上各增加3米,该长方形的面积是多少?
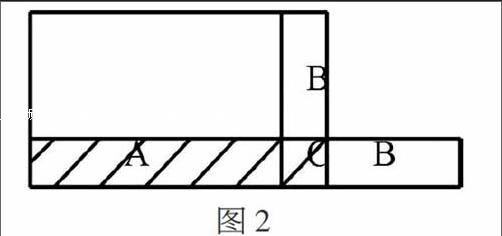
图2
在本题中没有已知长方形的长、宽,此时,教师可引导学生根据题意画出图形。首先,引导学生由长方形的周长48米,根据长方形周长公式(长+宽)×2,得出长+宽的值为24米。然后,可画出图形2,将图形B的位置剪切到C后面。从图形中不难发现,ABC重新组成一个新长方形,且该长方形的长是原来长方形的长与宽之和再加上3米,即可得到27米。根据长方形面积公式:长×宽,即:27×2=54米。
三、注重画图策略评析,培养学生画图解题习惯
画图策略的应用还需要教师加强画图的评析,在评析过程中培养学生画图解题习惯。通过运用客观评价的教学手段,可采用学生之间评价、教师评价及自身评价等多种评价方式,进而帮助学生更好地掌握各种数学知识及其技能。其中进行学生之间的评析时,教师可根据全班学生的个性、爱好、学习情况,分为四人一小组,在小组内对各自的画图解题进行评价,并从中选定一位组长,最终对小组评价结果进行总结及汇报。通过小组内评价,可使学生学习别人的优点,改正自己的缺点,达到共同学习的目的。
如:学习完“平面图像面积”内容后,教师可设置以下题目。
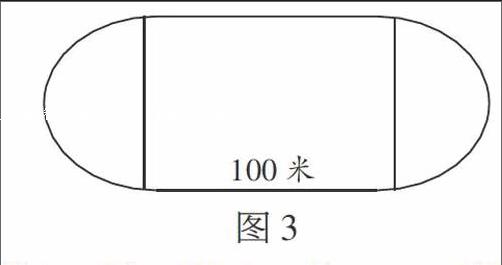
某学校运动场平面图如图3所示,已知中间长方形运动场的面积为6000平方米,边长为100米,求整个运动场的面积。
[100米]
图3
当学生看到该题时,可能会无从下手。此时,教师可实行小组合作学习,在小组内进行探究,每一位学生都将自己的解题想法讲给其他小组成员,让其他小组成员进行评价,实现互评。通过此番讨论,有的学生提出以下解答方案:根据长方形面积的计算公式:长×宽,即可得到:100×?=6000,宽为60米。图形两边为半圆,60米为半圆直径,根据圆形面积计算公式:π×半径×2,即可得到:π×(60÷2)×2=60×3.14=188.4平方米。最后将长方形面积加两个半圆面积得到整个运动场面积。通过这种教学评价,能够让学生较快理解题意,在解题过程中培养其画图解题习惯,提高解题技能。
四、总结
总而言之,数学具有较强的抽象性,通过应用画图策略可将复杂问题简单化、抽象问题直观性,有效提高解题水平。在此过程中,教师应创设画图解题情境、加强画图解题引导及注重画图策略评析,真正培养学生的画图解题思维能力,促进全面发展。
(责编 罗 艳)endprint

