“两步计算解决的实际问题”教学设计及设计意图

钱婷+++韦波富

教学内容：

苏教版小学数学三年级上册P11～12。

教材及学情分析：

这节课主要教学两步连除或乘除混合解决简单的实际问题。教材例题及习题大多以图文结合为主的呈现形式寓信息于画面和对话中，以培养学生收集、整理信息和利用条件解决问题的能力。学生学习这部分内容的知识基础是乘、除法的意义，解决问题的经验是用连乘解决两步计算的实际问题，这就为学生自主解决问题提供了可能。

本节课还有一个重要任务是引导学生寻找条件之间的关联性，进而构建数量关系模型，培养学生运用综合法解决问题的能力。

教学目标：

1.使学生经历用两步计算解决实际问题的探索过程，进一步深化对相关数量关系的认识，感受从已知条件出发或从所求问题出发解决问题的策略价值，能用两步连除或乘除混合正确解决问题。

2.运用几何直观等手段，引导学生进一步理解乘、除法的意义，感悟数量之间的关系，培养学生初步的建模意识。

教学过程：

一、自主探究，激活经验

1.观察分析。

师：同学们爱看书吗？（出示主题图）今天跟老师一起去图书馆参观一下吧。

师：从图中你看到了什么？（学生收集信息：2个书架，每个书架有4层，一共有224本书）

师：管理员要将这些书放到两个书架上，每层都要放，而且要放得一样多，应该怎样放？你能帮助管理员解决这个问题吗？用算式把你的想法表示出来。

【设计意图：数学源于生活，用于生活。该环节的教学对教材中的主题图进行了一番修改，这样使应用题变成了生活中的现实问题，利于学生理解。“应该怎样放”这一问题具有开放性和挑战性，比教材中“平均每个书架每层放多少本书”的问题更有探究性。】

2.交流思路。

（师出示学生的两种算法）

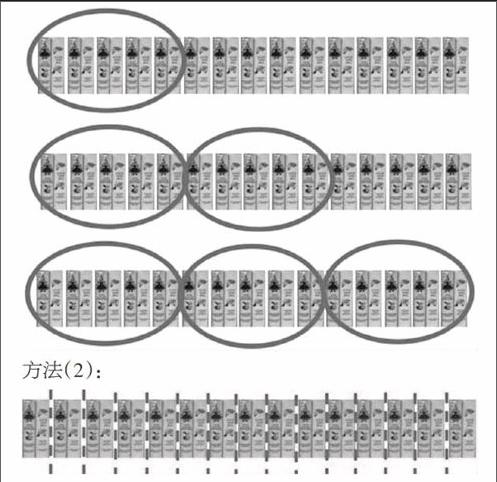
方法（1）：224÷2=112（本） 方法（2）：2×4=8（层）

112÷4=28（本） 224÷8=28（本）

师：每一步求的是什么？根据哪两个信息求的？

师：为什么用除法或乘法？（课件动态演示每种方法平均分的过程）

方法（1）：把224本书用一个大长方形表示，先平均分成2份，再用除法求出每个书架有112本书，最后求出每层放多少本书。

[224本] [？本][112本]

方法（2）：每个书架有4层，先求出两个书架有8层，再用除法求出每层放多少本书。

[？本]

【设计意图：独立解决问题的过程就是自主探寻解决问题思路的过程。“每一步求的是什么”“根据哪两个信息求的”等问题，既是引导学生思考方向的发问，又是综合法策略运用的体现。几何直观能帮助学生理解数量关系，既沟通了图形与算法之间的内在联系，又丰富了知识的表象，建立了应用连除或乘除解决实际问题的意识。】

3.尝试检验。

师：平均每个书架每层有28本书对不对呢？我们可以怎样检验？

【学生可以用28×4=112（本）、112×2=224（本）或2×4=8（层）、8×28=224（本）来检验。】

【设计意图：引导学生对结果进行检验，既沟通了与前面学习的用两步连乘解决问题之间的关系，又使学生构建了良好的认知结构。】

4.反思比较。

师：这两种方法在解题思路上有什么不同？在解决问题的策略上有什么相同的地方？

【设计意图：比较的过程是反思的过程。这个环节，旨引导学生思路上求异、策略上求同，突出解决问题策略的价值。】

二、尝试实践，迁移经验

师：刚刚大家用不同的方法帮阿姨解决了问题。（课件出示下图）看，这里还有一些书呢！

[，][。]

1.学生了解信息，尝试解决问题。

2.呈现学生的解题方法。

方法（1）：2×5=10（本），30÷10=3（层）;

方法（2）：30÷2=15（套），15÷5=3（层）。

3.交流：根据哪两个信息求出了什么？为什么用乘法（除法）？

4.直观出示乘法和除法的解题图示。

方法（1）：

方法（2）：

【设计意图：这一环节的教学是上一个情境的延续，在同一个情境里安排了两次不同的放书活动，且这两个活动中数量之间的关系迥然不同。这个情境是“等份除”及“包含除”的综合运用，数量关系复杂，且不易发现。安排这一环节，既让学生用刚刚习得的方法、经验解决当前问题，又让学生体会到更多的数量关系，实现“以一例带一片”的教学目的。】

三、拓展应用，丰富经验

1.师：有位小朋友生病了，医生给他开了一瓶药（出示下图），这瓶药可以吃多少天？你能解决吗？试试看。

（若有学生质疑或做不出来，师追问：为什么做不出来？）

生：少条件。

师：还需要知道什么条件？（出示：这瓶药一共有150片）

（学生独立完成后全班交流：每一步求的是什么？是根据什么条件求的？为什么这样列式？）

【设计意图：将教材中“一共有150片”这个条件省去，旨在引导学生寻找条件间的关联性，有效构建数量之间的相互关系，使他们懂得从问题出发思考问题解决的策略。】

2.出示题图（如下）。

[共384箱]

师：从图中看到了什么？能提出一个两步计算的问题吗？

生：平均每辆汽车每次运多少箱？

师：用一句话将条件和问题完整地叙述出来，并说说你是怎么解决这个问题的。

【设计意图：教学中没有直接出示问题，而是要求学生自己提出两步计算的问题，这其实就是学生寻找条件之间关联性和构建数量关系模型的过程。学生在这一过程中需要根据两个已知条件解决一个问题，再根据这个结果与已知条件的关联性提出另一个问题。同时，“用一句话将条件和问题完整地叙述出来”既是图文应用题向文字应用题的过渡，又是培养学生整理信息能力的需要。】

3.师：周末的时候，小明和小刚去买羽毛球拍（出示下图），请你来帮他们算算，每个羽毛球拍多少元？

（1）出示学生的三种解法。

方法①：192÷2=96（元），96÷4=24（元）;

方法②：2×4=8（个），192÷8=24（元）;

方法③：2+4=6（个），192÷6=32（元）。

（2）组织学生讨论，辨析对错。

（3）师（小结）：看来，在解决问题时，要具体问题具体分析。

【设计意图：这个环节把教材中“我们每人买2个羽毛球拍”改成“小明买2个羽毛球拍，小刚买4个羽毛球拍”，目的是为了打破学生的思维定式，不让学生以为学习了连除或乘除解决问题，所有的习题都要用这种方法解答，使学生养成认真审题的习惯。通过辨析，启发学生在解决问题时结合所要解决的问题，根据运算意义，弄清相关联的两个条件之间可以建立怎样的关系。】

……

总的设计说明：

整个教学设计充分体现了用解决问题的理念指导应用问题的教学，具有问题色彩、探究意味，突出了综合法解决问题策略的指导应用，并借助几何直观引导学生进一步掌握两步计算解决问题的思路，理解解决此类问题时每一步算式的意义。同时，教师注重引导学生应用四则运算的意义以及积累的经验解决问题，建立数学模型，促进数量关系的理解，感悟解题策略，积累解决问题的基本方法和经验，从而使他们在数学与生活之间架起一座沟通的桥梁，体现数学的应用价值。

（责编 杜 华）endprint