依据认知水平 导引自觉自为

叶小飞

课程标准指出，数学课程内容的选择要贴近学生的实际，有利于学生体验和理解、思考与探索，教师教学应该以学生的认知发展水平和已有的经验为基础，面向全体学生，注重启发式和因材施教。因此，教师应根据学生思维、智力的发展水平，设置适当的数学活动情境，以便学生能在情境的驱动下独立思考、获取知识、发展思维，自主进行数学学习。

一、无限遵从认知发展的阶段性

皮亚杰认为，人的认知发展是一个认知图式不断重建的过程，并以符号逻辑为工具，采用逻辑和数学的概念来描述发展阶段的特征，把“运算”水平当作认知发展阶段的依据，将认知发展划分为感知运动、前运演、具体运演和形式运演四个阶段。

这一发展阶段理论已经被许多实验所证实，被国际心理学界所普遍接受。我以为，我们必须重视皮亚杰所说的思维发展顺序问题、发展的连续性问题以及在具体思维过程中的“反祖”现象。

比如在解答“工程队修一条30千米长的公路，3天修了全长的25%，照这样计算，多少天能修完这条公路？”时，有的学生先算出3天修的千米数（30×25%），再算出1天修的千米数（30×25%÷3），最后算得修完全长一共需要多少天（30÷（30×25%÷3）），认为这样做“顺理成章”;有的学生却能跳过具体的数量，避开繁琐的计算，一步计算求得修完全长一共需要的天数（3÷25%），而有的学生即便到了六年级第二学期仍然对这一思路表示“看不懂”。对此，作为教者应该表示理解，不能强求“顺理成章”的那部分学生立刻接受后者“先进的思路”，因为即使在学生的思维发展到形式运演阶段后，具体运演行为仍然是存在的，并且日益整合为一个形式运演更加综合的系统，他们在数学活动中也并不只是运用形式运演思维，还经常地借助低阶段的思维，特别是面临新的知识时，他们常常重新回到具体思维阶段，有时甚至是回到前运演思维阶段上，他们在进入抽象思维形式之前，总是要先获得新知识领域的具体经验的。

二、有心促成数学认知的阶段性发展

在遵循学生的认知特点的基础上，教师不仅要求学生充分、详尽地“展开”思维，而且要有意识地引导学生对思维过程加以“压缩”，据情拿捏好两者之间的火候，促进学生的数学认知在“阶段”中有活力地“发展”。

1.从“正确性”走向“灵活性”

在数与运算中，初始阶段要严格要求用计算法则进行思考，按照规定的运算顺序一步一步地进行计算，保证运算的正确性;思维活动展开后要及时加以压缩，省略或简化中间过程，以提高计算的熟练程度，迅速得出计算结果。

如计算“7-2 ”，在初期应要求学生按“原式=6 -2 =4 ”的过程展开，以促使学生在计算过程中充分地理解算理，但熟练之后又要及时提出简化的要求，即“原式=”，促进学生的思维层次跃上一个新的台阶。

又如，对于形如“3.7×99+3.7”一类的简便计算题，为了训练学生理解并掌握乘法分配律，可特别规定暂不允许运用“99个3.7加上1个3.7”的思路（即原式=3.7×100）解答，而“逼迫”学生运用乘法分配律进行简算，一步一步地写出完整的思维过程（即原式=3.7×99+3.7×1=3.7×（99+1）=3.7×100=370），待学生对乘法分配律熟悉后，再放开限制，允许并鼓励学生从多个角度来解决问题。

2.从“分解”走向“简化”

在图形与几何中，组合图形面积的计算对培养学生综合运用几何初步知识解决简单实际问题的能力、空间想象能力以及逻辑思维能力都有很大作用，但初始阶段，学生的思维活动应是展开的。

如图1，圆的半径是4厘米，求阴影部分的面积（单位：厘米）。

图1 图2

因为组合图形面积计算的学习刚刚开始，所以要让学生一步一步地分解，以形成求组合图形面积的基本思路，即S阴= + =（SA-SB）+（SB- SA），其中SA表示直角扇形的面积，SB表示等腰直角三角形的面积。但是，若只满足于会解是不够的，因为像基本思路那样解答，不仅计算比较繁琐，且不利于培养学生思维的灵活性，因此，必须引导学生观察、动手实践，运用割补、翻折、旋转、平移、等积变形等手法，扩展思维，即通过如图2的两次翻折，则S阴= SA（即 S圆）= ×3.14×42=6.28（平方厘米）。

3.从“问题解决”走向“数学地思考”

“综合与实践”是一类以问题为载体、以学生自主参与为主的学习活动，但教师不能以问题的解决作为教学的最终目标，而要根据不同学段学生的年龄特征和认知水平，根据学段目标，合理设计并组织实施“综合实践”活动，引导学生展现思考过程、提升活动经验，学会“数学地思考”。

比如学习了三角形、平行四边形和梯形的知识后，就设计“认识五角星”的实践活动，组织学生用小棒制作五角星，用纸笔画五角星，用剪刀剪五角星，有序地数五角星中分别有多少个三角形、多少个平行四边形、多少个梯形，以及推断五角星的内角和是多少度;学完长方体与正方体，又设计“火柴盒的面积计算”的实践活动，组织学生测算火柴盒的表面积与体积，以及火柴盒外套、内盒所用硬纸的面积……

三、导引认知发展走向自觉行为

1.“要把学生造就成一种什么人，自己就应当是什么人。”——[俄]车尔尼雪夫斯基

郑毓信老师曾说：“应当在数学教学中充分发挥数学的文化价值！”如何充分发挥？我们不应脱离具体数学知识内容的学习去空谈情感、态度和价值观的培养，而应当突出强调文化价值与知识内容的相互渗透，真正做到“以知怡情”;应该坚持认为，自我的数学教学应当首先是读“人”的，应满足于在任何时候总能充当学习的“样板”，因为文如其人，一个没有数学味的教师又怎能真正上出具有数学味的数学课来？所以唯有加强学习，自觉修炼，提升素养，“努力将文化落实到人格”，方能实现数学文化导引学生的自觉。

2.“教育不是注满一桶水，而是点燃一把火。”——[爱尔兰]叶芝

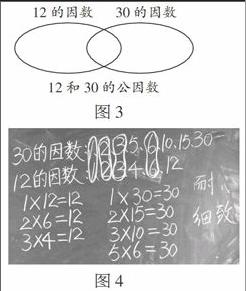
有一次在批改学生作业时，发现在有道题目（如图3）写错的人数较多，多数是漏写一、两个因数。为什么会漏写呢？怎样才能使学生不漏呢？我首先问学生：“这一题，许多同学总是因漏写因数而出错。谁来介绍介绍，怎样做就能不漏写因数？”学生甲在黑板上一边讲解一边写出了解这道题的全过程（如图4）。

图3

图4

我并不满足于学生掌握了解这类题的方法，又提议：“请大家评价一下学生甲。”于是，学生你一言我一语，有说书写认真的，有说思路清晰的，还有说不怕麻烦的。我则趁热打铁：“同学们，什么叫做作业耐心细致？这就叫耐心细致。大家说，像这样做的作业，还会漏写因数吗？”至此，耐心细致已经水到渠成地进入学生的头脑中。

发自内心地认同“一个被迫认识错误的人不会改变其原有观点”，而正确地运用心理“战术”，就是这么威力无穷！

（责编 金 铃）endprint