轴向磁通空气心永磁同步发电机的谐波抑制
上官璇峰,李毅搏,邵建伟
(1.河南理工大学,焦作454000;2.渑池县供电局,三门峡472400)
磁场的求解必须满足以下边界条件:
0 引 言
考虑到全球能源消耗等问题,风力发电的装机容量迅速增长[1]。近年来风力发电行业迅猛的发展,永磁技术的进步使紧凑高效的永磁风力发电机成为现实。轴向磁场空气心永磁同步发电机(AFAPMSG)质量轻、效率高、体积小、适应于低速运行[2]。这些优点决定了它在直驱式风力发电应用上的广阔前景。工业上对同步发电机的电动势波形的正弦性有严格的要求,实际电动势波形与正弦波形之间的偏差度用电压波形的总谐波失真度THD来表示。为了减小电压波形的总谐波失真度,除采用分布绕组、短距绕组、正弦绕组外,还应改善气隙磁密波形,它不但与气隙形状和极弧系数有关,还与有无软铁极靴和稳磁处理方法有关[3]。国外学者Tareq S. El-Hasan 和Patrick C. K. Luk 采用等体积等表面积的半圆形和梯形永磁体来改善轴向磁通永磁同步发电机的电势谐波[4]。国内对轴向磁通永磁同步发电机关于削弱电势谐波的研究相对较少,文献[5]提出在径向磁场永磁电机中采用正弦形表面的永磁体可以使空气域磁密趋近正弦分布,并且采用弧形永磁体进行了有限元计算与分析。
本文采用正弦形的永磁体(即永磁体充磁方向厚度沿圆周方向为正弦分布)的AFAPMSG,并通过有限元方法计算电机的气隙磁密分布和电机的空载电动势。为了反映采取不同措施时的优化效果,还对磁密波形及电动势波形分别进行了THD值的计算和分析。
1 空载磁场计算
假设磁密大小为正弦分布,如图1 所示。

图1 标准正弦磁密分布

如图1 所示,在一个周期内,两个线圈边分别位于α1和α2处,两线圈边的电动势分别如下:
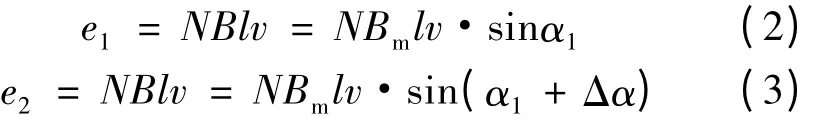
整个线圈电动势:

式中:N 为线圈匝数;l 为线圈边有效长度;v 为线圈边的线速度。
AFAPMSG 通过永磁转子产生的旋转磁场与绕组线圈交链产生电动势,由式(1)~式(4)可得出结论:无论采用整距线圈还是短距线圈,如果磁密随时间为正弦变化,则线圈电动势波形都为正弦波形。
磁密波形的改善可以采用以下方法:调整极弧系数[3]、改善磁极表面形状[5]、Halbach 阵列[6]、控制永磁体的充磁量以及分块儿永磁体[7]。
文献[5]选用接近于正弦的弧形表面永磁体(图2(b)),进行了有限元分析计算,得出采用弧形永磁体可以削弱电动势的5 次和7 次谐波的结论。
文献[8]对矩形永磁体(图2(a))AFAPMSG 的空载磁场、电枢反应磁场以及复合磁场计算做了详细的分析计算,本文重点验证正弦形永磁体(图2(c))的磁密波形更加趋近正弦波形,因此,只做空载磁场的解析计算。

图2 转子扇形永磁体周向切面
1.1 正弦形永磁体空载磁场计算
对于正弦形永磁体结构AFAPMSG 的空载磁场计算模型如图3 所示。简便起见,选用直角坐标系来进行磁场的2D 求解。变量X 代表半径为R 处所需计算磁场的圆柱切面沿圆周方向的距离。变量y代表从贴有永磁体的转子轭表面开始计算的轴向距离。图3(a)中Lm表示永磁体在半径r 处沿圆周方向的长度。αp表示永磁体极弧系数,τp表示节距,hm表示对应x 位置永磁体充磁方向厚度,Hm表示永磁体充磁方向厚度按照正弦规律变化的幅值,L 表示两转子铁轭之间的距离。图3(b)中磁场强度M0=Br/μ0表示正弦形永磁体对应的磁场强度幅值。
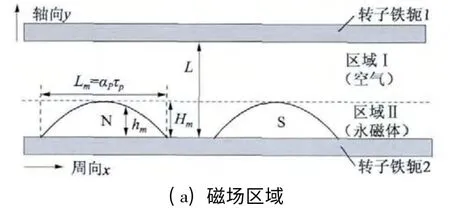

图3 AFAPMSG 空载磁场计算模型
本文重点考虑轴向磁场沿圆周方向的变化,因此,只对By进行简单推导、计算。为计算方便,仅对单个磁极的静态磁场进行解析计算。对于正弦形永磁体结构的AFAPMSG,如图3(a)所示,永磁体充磁方向高度:

式中:Hm为永磁体厚度按照正弦规律变化的幅值;Lm为永磁体在半径r 处沿圆周方向的长度。参照文献[8]对矩形永磁体的计算方法,空气隙部分(区域Ⅰ)以及永磁体部分(区域Ⅱ)的磁场标量磁位:

磁场强度部分用标量磁位φ 表示:

磁场的求解必须满足以下边界条件:

由边界条件可知,系数C1~C4中将含有hm(x),而正弦永磁体高度hm(x)为一个关于自变量x 的函数,因此利用边界条件求解系数时需要考虑系数C1~C4对x 偏导数的问题。通过上述边界条件,式(6)、式(7)中的系数C1~C4如下表示:
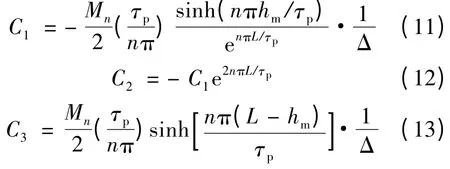

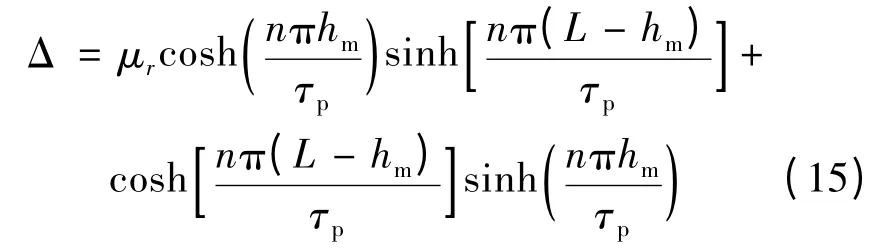
式中:空气部分(区域Ⅰ)和永磁体部分(区域Ⅱ)的y 向磁密表达式如下:
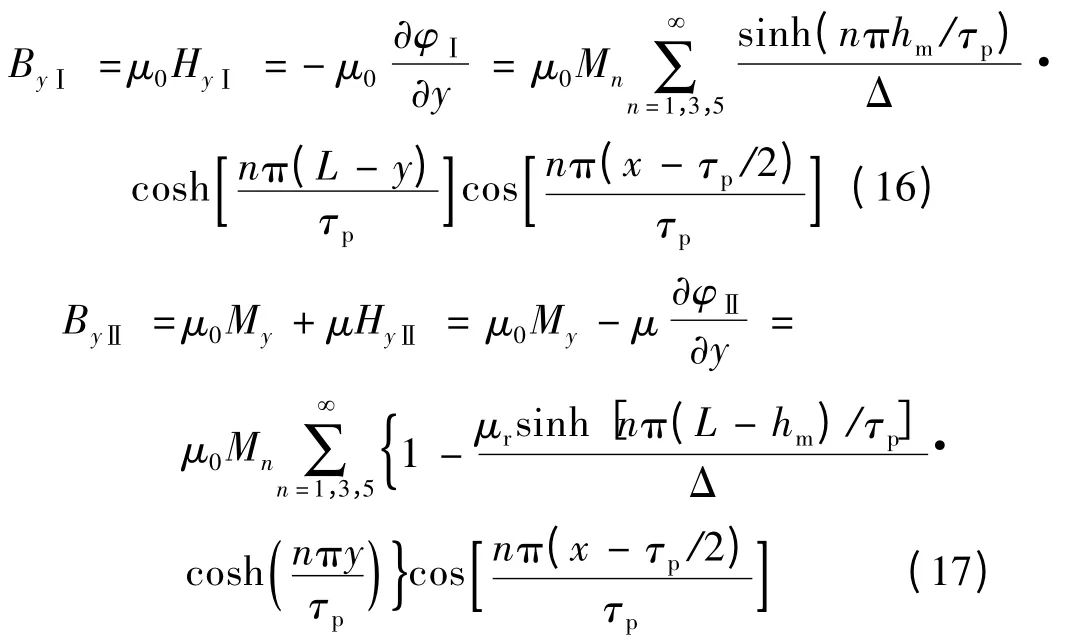
1.2 双边正弦形永磁体空载场计算
对于双边永磁转子结构的AFAPMSG,如图4 所示。因为假设磁场线性,因此双边永磁体的磁场可以分开计算,最后的磁场直接叠加即可。由式(16)和式(17)可知,在双边结构轴向磁场永磁电机中,三个区域中的磁密表达式:


图4 双边永磁转子结构的AFPMSG 磁场计算模型
2 计算结果及分析
由于短距绕组能够抑制电动势谐波[9],因此通过整距绕组的AFAPMSG 有限元模型进行仿真计算,可以更好地检验采用正弦形永磁体对电动势谐波的抑制效果。
建立正弦形永磁体电机的FEM 模型如图5 所示,不同极弧系数情况下,永磁体的最大厚度保持相等。在有限元分析软件MagNet 中进行静态磁场的有限元计算。有限元模型结构为中间单层定子绕组,双边外永磁转子结构的AFAPMSG。由于该模型需要进行3D 有限元分析,而全模型计算耗时太长,因此,可以采用一对极(即1/3 模型)、一相绕组的一个整距线圈来进行有限元计算。模型参数如表1所示。

图5 双边永磁转子结构的AFAPMSG 的3D 视图
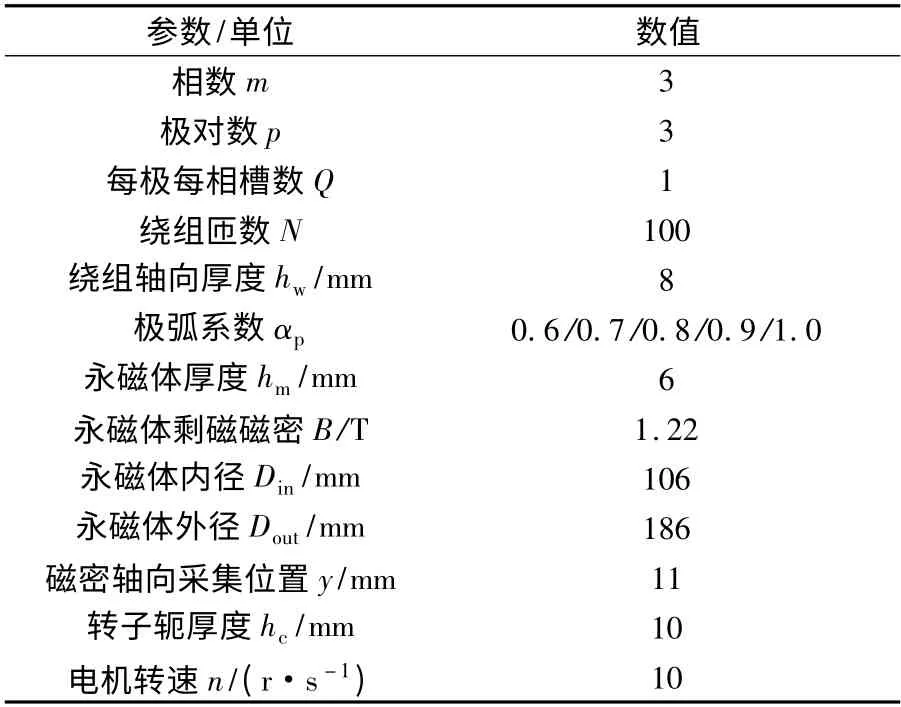
表1 电机有限元模型参数
2.1 磁密分布
由于本文为空气心AFPMSG,绕组是通过浇注环氧树脂固定的。FEM 模型中,绕组周围设置为空气。因此,可以取绕组轴向中间位置y =11 mm,半径73 mm 处沿圆周方向分布的磁密,由上述可知,双边正弦永磁转子中y=11 mm 处的复合磁场的磁密:
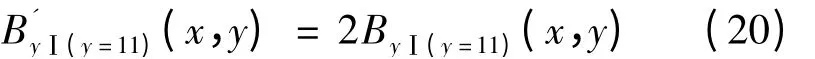
解析法计算结果与FEM 计算结果如图6 所示。
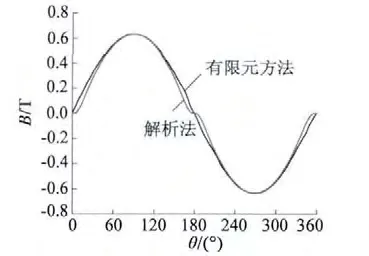
图6 双边正弦形永磁体复合磁场沿圆周方向磁密波形
图6 表明,通过解析法与有限元方法计算双边正弦形永磁体励磁磁场的计算结果比较吻合,并且正弦形永磁体励磁产生的磁密沿圆周方向的分布非常接近正弦波形。
2.2 极弧系数的影响
总谐波失真度THD是表征波形相对正弦波畸变程度的一个性能参数,其定义为不大于某特定阶数n 的全部谐波分量有效值Gk与基波分量有效值G1比值的方和根。即:
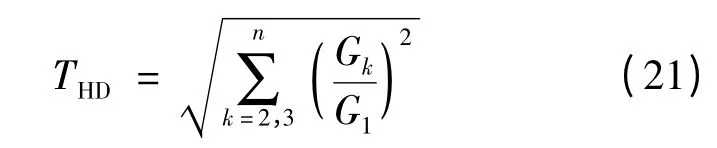
因此,可以采用参数THD来衡量正弦形永磁体对磁密和电动势波形的优化效果。文献[3]指出,气隙磁密波形与气隙形状和极弧系数αp有关。取αp=0.6,0.7,0.8,0.9,1.0 建立不同极弧系数的正弦形永磁体AFPMSG 的有限元模型。不同极弧系数下的永磁体充磁方向厚度曲线都是幅值相同而周期不同的半周期正弦波形。在MagNet 中进行含运动部分的动态求解,并整理求解数据。
图7 所表示的是,不同极弧系数情况下,单个磁极上方的磁密波形。图7 中,从内测到外侧的曲线所对应的极弧系数依次增大,外侧曲线比内侧曲线更加接近正弦波形,而曲线幅值基本一致,并且N极与S 极交界处磁密波形有畸变。可以得出结论,随着极弧系数的增大,正弦形永磁体所产生的磁密波形更加趋近正弦。
图8 所表示的是,不同极弧系数情况下,一个周期的电动势波形。图8 中,从内测到外侧的曲线所对应的极弧系数依次增大,外侧曲线比内侧曲线更加接近正弦波形,而曲线幅值基本一致,并且在N极与S 极磁极交接部分的电势畸变情况随着极弧系数的增大而减小。可以得出结论,随着极弧系数的增大,正弦形永磁体所产生的电动势波形更加趋近正弦。

图7 不同极弧系数情况下y=11 mm 处磁密波形

图8 不同极弧系数电动势波形
图9 所表示的是,利用总谐波失真度THD来体现不同极弧系数的磁密波形和电动势波形相对于标准正弦波形的畸变程度。图9 中,随着极弧系数的增大,磁密波形与电动势波形的THD值逐渐减小,并且电动势波形THD值曲线紧靠在磁密波形THD值曲线的上方。因此,可以得出结论,对于正弦形永磁体励磁的AFAPMSG,随着极弧系数的增大,气隙磁密波形和电动势波形总谐波失真度逐渐降低,波形更加接近正弦波形。
图10 中,设定极弧系数为1 时,磁密基波大小为1、永磁体质量为1。纵轴表示一个相对值,不同极弧系数相对于极弧系数为1 时的磁密相对值和永磁体质量相对值。由图10 可以得出结论,随着极弧系数的增加,磁密的基波幅值和永磁体的用量都呈上升趋势。
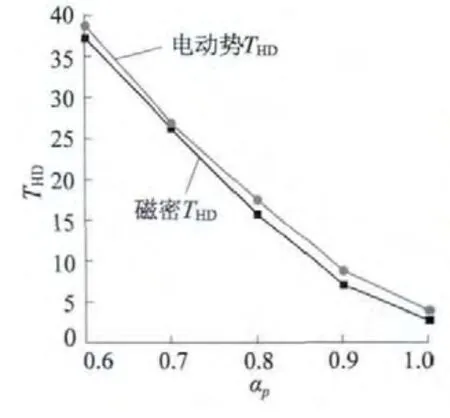
图9 磁密与电动势波形的总谐波失真
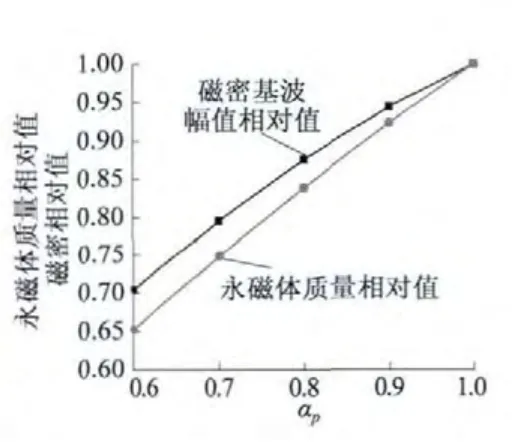
图10 不同极弧系数情况下,磁密与永磁体质量相对于各自基值的变化
3 结 语
AFAPMSG 的电动势很大程度上取决于气隙磁密的分布,采用正弦形永磁体可以使电机空气域磁密波形更趋近正弦,进而使得发电机电动势波形相对标准正弦波形的畸变程度更低。通过有限元仿真计算,采用正弦永磁体的AFAPMSG 沿圆周方向的磁密波形以及动态计算电动势波形随着电机极弧系数的增大,两者波形的THD逐渐降低,达到预期效果。在传统径向磁场PMSG 中,也可以采用正弦形永磁体、电机极弧系数为1 的方法改善发电机电动势的波形。采用正弦形永磁体的发电机不用通过电力电子技术就可以得到更加正弦的电动势波形,并且节省永磁体用量,减小电机制造成本和发电成本。
[1] KOBAYASHI H,DOI Y,MIYATA K,et al. Design of axial-flux permanent magnet coreless generator for the multi-megawatts wind turbines[C]//EWEC2009.
[2] WANG R J,KAMPER M J,VAN DER WESTHUIZEN K,et al.Optimal design of a coreless stator axial flux permanent-magnet generator[J]. IEEE Transactions on Magnetics,2005,41(1):55-64.
[3] 唐任远.现代永磁电机理论与设计[M]. 北京:机械工业出版社,1997:290-291.
[4] EL-HASAN T S,LUK P C K.Magnet topology optimization to reduce harmonics in high-speed axial flux generators[J]. IEEE Transactions on Magnetics,2003,39(5):3340-3342.
[5] 常九健,马文礼,黄金龙.永磁同步电机永磁体形状分析与优化[J].大电机技术,2012(2):15-18.
[6] HALBACH K.Design of permanent multipole magnets with oriented rare earthcobalt material[J]. Nuclear Instruments and Methods,1980,169(1):1-10.
[7] 黄晟,任智杰,黄科元,等.永磁同步电动机磁密优化方法研究[J].微电机,2009,42(10):26-28.
[8] CHAN T F,LAI L L,XIE Shun-ming. Field computation for an axial flux permanent-magnet synchronous generator[J]. IEEE Transactions on Energy Conversion,2009,24(1):1-11.
[9] 汤蕴璆,罗应立,梁艳萍.电机学[M].北京:机械工业出版社,2008:136-137.

