基于模糊PI 和自适应滑模的异步电动机DTC 控制
李 瀛,胡立坤,卢子广,李 卓
(广西大学,南宁530004)
0 引 言
20 世纪80 年代中期,Takahashi 和Noguchi 提出了直接转矩控制理论,直接转矩系统结构简单,具有优良的动静态控制性能和调速效果[1-2]。
然而,直接转矩控制有一些不足之处,电机运行时存在转矩、磁链脉动大,调速范围也受到一定的限制。通常直接转矩控制技术(以下简称DTC)转速调节部分采用PI 调节器,通过给定转速与实际转速的差值得到给定转矩的值。由于电机参数在不同的运行状态中不断变化,而传统的PI 调节器不能提供良好的控制要求,转速的控制精度较差,不利于其精确调节[3]。多年来,国内外专家学者在磁链观测器和PI 参数调节方面作了大量研究[4-6]。文献[7]采用滑模控制设计转速环和转矩环,减小了电机的响应时间和转矩脉动。文献[8]采用多电平逆变器减小了磁链和转矩的脉动,但使系统的硬件结构变得复杂。文献[9]提出的速度观测器和磁链观测器,可适用于直接转矩控制。文献[10-11]均能有效减少转矩脉动,但在转矩控制回路中采用PI 控制器使转矩响应变慢。
本文基于以上问题,提出模糊自适应PI 控制和自适应滑模磁链观测器的设计,其中模糊PI 代替传统的PI 控制,实现转速的精确控制,而磁链观测器中的自适应收敛律是通过Lyapunov 理论推导出来的,可保证观测器的稳定性,所估计的转矩、磁链具有较高的精度,脉动较小,弥补了DTC 的不足。最后,通过dSPACE DS1104、QUANSER8(Q8)搭建硬件的在回路平台进行实验,验证了两种策略所具有的优良性能。
1 异步电动机数学模型和控制系统结构
1.1 异步电动机数学模型
静止坐标系下异步电动机的数学模型、定子磁链空间矢量角位置以及αβ 坐标系下定子磁链和电磁转矩的公式如下:
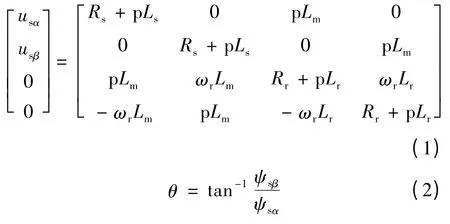

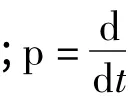
1.2 改进的直接转矩系统控制结构
为适应实际的应用系统,常采用速度观测器DTC 技术,本文采用自适应滑模方法设计磁链观测器,同样可以估计转速。用模糊PI 控制器代替传统的PI 控制器来控制转速。改进的异步电动机DTC系统框图如图1 所示。

图1 改进型DTC 系统结构框图
2 模糊PI 控制器设计
模糊控制理论常用于优化异步电动机的性能[12]。本文所采用的模糊自适应PI 控制器是一个双输入、双输出的系统,以误差e 和误差的变化ec为输入量,以ΔKp,ΔKi为输出变量。根据模糊PI控制的基本思想,依照实际经验建立模糊控制规则表,如表1、表2 所示。误差e 和误差的变化ec的论域范围为[-12,12],ΔKp,ΔKi的论域范围分别为[-6,6],[-0.6,0.6],e,ec,ΔKp,ΔKi的模糊集合均取{NB,NM,NS,ZO,PS,PM,PB},表示{负大,负中,负小,零,正小,正中,正大}。其中,NM,NS,ZO,PS,PM 均取三角波隶属函数。边界值NB,PB 取梯形波隶属函数。

表1 ΔKp 的模糊控制表

表2 ΔKi 的模糊控制表
3 磁链观测器设计
将αβ 坐标系下异步电动机定子电流和定子磁链写成状态方程:

建立观测器模型:

用式(7)减去式(6)得:




由式(10)得:

将式(10)代入式(11)消去S 得:

选取李雅普诺夫函数为:

由于转速ωr变化慢,可将其近似为常数,Δωr=0,则V 的导数:

式(13)变为:

将式(11)和式(12)代入(15)中得:

为了满足李雅普诺夫稳定条件,使pV <0,可令z1<0 并且z2=0。故,为保证z1<0,可使:

将K 写成KT=cI+dJ,代入式(18)得:

改写:

令W= [wI-KP12],得KP12的特征根:

令行列式为零,得:
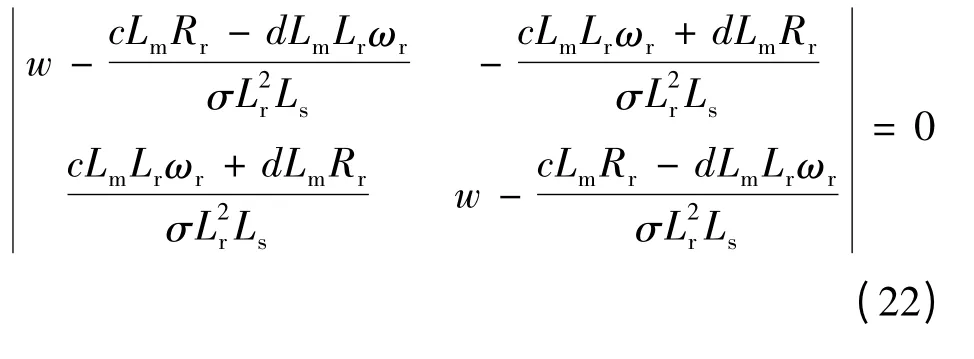
即:
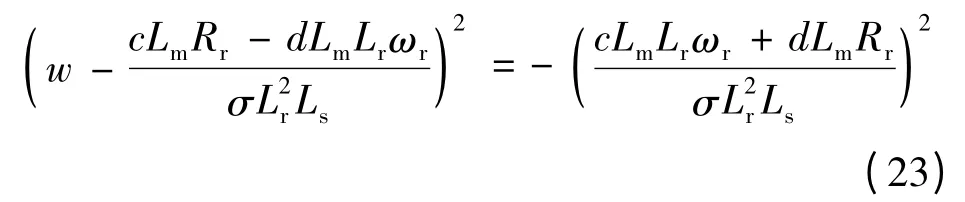
则特征根为:


因为w >0,特征根非正,磁链观测器系统是稳定的。而当z2=0 时,有:

这样,pV <0,将式(18)代入式(26),得:

因此,通过上式估算磁链,可替代式(5)传统磁链计算法。新型磁链观测器也可估计转速,并能根据观测的磁链值计算电机转矩值。
4 仿真结果
依据DTC 原理、异步电动机模型和控制设计方法,用MATLAB/Simulink 分别搭建传统和新型的DTC 仿真模型。仿真电机参数如表3 所示。

表3 仿真电动机主要参数


图2 传统异步电动机直接转矩控制仿真结果

图3 新型异步电动机DTC 仿真结果
由图2、图3 可知,两种方法中电机转速均能跟踪给定转速,当给定转速发生改变时,电机转速迅速达到1 000 r/min,定子磁链在整个变化过程中没有发生改变,一直为0.8 Wb,转矩也呈矩形。但是新型直接转矩控制方法调节速度快,转矩、磁链脉动小。
5 实验结果
以上仿真结果证明了改进方法的可行性和有效性,将其应用到实际系统中进行实验研究。本实验采用一套4 kW 三相异步电动机、QUANSER8(Q8)和dSPACE DS1104 搭建调速实验平台,dSPACE DS1104 实时仿真系统是一套基于MATLAB/Simulink 的控制系统开发及半实物仿真的软硬件工作平台,可作为控制器进行实时计算、A/D 采样、PWM脉冲输出和数据保存。采样频率50 kHz,开关频率5 kHz,死区时间5 μs。异步电动机主要参数如表4所示。
实验中给定转速从200 r/min 上升到600 r/min,模糊PI 控制器和传统PI 控制器对比结果如图4 所示。由图4 可看出,模糊自适应PI 大约经过150 ms转速就达到稳定状态,并且无超调和机械脉动,而传统的PI 要经过250 ms 转速才稳定,大约有5.25%的超调。

表4 异步电动机主要参数

图4 模糊PI 和传统PI 的对比
图5 为自适应滑模磁链观测器所观测的磁链、转矩与传统磁链、转矩对比实验。给定磁链为0.75 Wb,电机先空载运行,在1.0 s 时带载运行。图5(a)、(b)为传统方法中的转矩、磁链波形图;图5(c)、(d)为采用新型磁链观测器的转矩、磁链波形图。
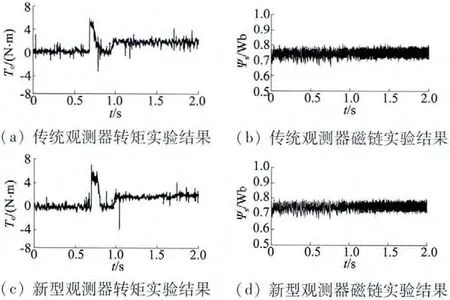
图5 两种观测器对比实验结果
从图5 可以明显看出,传统观测器所观测的转矩和磁链脉动很大,而采用自适应滑模设计的观测器,所估计的转矩和磁链脉动明显减小,说明观测器具有可应用性且控制性能优良。
将模糊PI 控制器和自适应滑模磁链观测器两种控制策略应用到异步电动机直接转矩控制调速实验中。给定定子磁链ψ*s =0.6 Wb,给定转速从300 r/min 上升到700 r/min。实验结果如图6 所示,图6(a)为转子速度,在0.7 s 时,转速发生从300 r/min发生跳变,大约经过0.16 s 转速上升到700 r/min,转速略有波动,变动范围很小。图6(b)为电机的电磁转矩,可以看出当转速发生变化时,转矩迅速响应,瞬间达到大约5.8 N·m,而后快速下降。图6(c)为定子电流变化,定子电流在高速时幅值比低速时小,定子电流变化到稳定的时间和转速上升所用时间几乎一致。图6(d)为定子磁链,在转速变化过程中,其值一直为给定磁链值,控制良好且波动很小。


图6 新型异步电动机直接转矩控制实验结果
6 结 语
本文的模糊PI 控制器是在传统PI 的基础上加入模糊控制算法,可自动调节PI 参数,转速调节时间短且无超调,实现其精确调节。根据自适应滑模基本原理,通过Lyapunov 理论推导自适应收敛律,设计了磁链观测器,所估计的转矩和磁链精度较高,脉动明显较少,两种控制策略提高了整个电机调速系统的控制精度,系统具有良好的控制性能。
[1] CHE Changjin,QU Yongyin.Research on drive technology and control strategy of electric vehicle based on SVPWMDTC[C]//2011 International Conference on Mechatronic Science,Electric Engineering and Computer. IEEE Conference Publications,2011:44-49.
[2] SERGAKI E S,MOUSTAIZIS S D.Efficiency optimization of a direct torque controlled induction motor used in hybrid electric vehicles[C]//IEEE Conference Publications,2011:398-403.
[3] 袁登科,徐国卿,胡波,等.直接转矩控制交流调速系统转速调节器的设计研究[J].机电一体化,2008(10):47-50.
[4] FINCH J W,GIAOURIS D. Controlled AC electrical drives[J].IEEE Trans.on Ind.Electron,2008,55(2):481-491.
[5] 吴志飞,张兴华,孙振兴,等.基于自适应滑模观测器的感应电动机直接转矩控制[J].微特电机,2013,41(10):64-69.
[6] 李春杰,李旭春.一种改进的直接转矩控制系统定子磁链观测方法[J].电机与控制应用,2006,33(6):32-35.
[7] 傅洪,陈全世,田光宇.基于滑模的直接转矩控制车用驱动电机的研究[J].汽车安全与节能学报,2010,1(1):59-66.
[8] 骆光照,李斐,杨南方,等.三电平逆变器供电永磁同步电机直接转矩控制研究[J].西北工业大学学报,2012,30(1):22-26.
[9] 廖永衡,冯晓云,王珍.基于定子磁链滑模观测器的异步电机空间矢量调制直接转矩控制[J].中国电机工程学报,2012,32(18):88-97.
[10] TANG Lixin,ZHONG Limin,RAHMAN M F,et al. A novel direct torque controlled interior permanent magnet synchronous machine drive with low ripple in flux and torque and fixed switching frequency[J]. IEEE Transactions on Power Electronics,2004,19(2):346-354.
[11] 刘军,楚小刚,白华煜. 基于参考磁链电压空间矢量调制策略的永磁同步电机直接转矩控制研究[J]. 电工技术学报,2005,20(6):11-15.
[12] AZCUE P J L,RUPPERT E. Three-phase induction motor DTC-SVM scheme with self-tuning PI-type fuzzy controller[C]//2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery.IEEE Conference Publications,2010:757-762.

