基于无差拍的永磁同步电动机直接转矩控制方法研究
唐红雨,刘贤兴
(1.镇江高等专科学校,镇江212003;2.江苏大学,镇江212013)
0 引 言
永磁同步电动机(以下简称PMSM)以其可靠性好、效率高、适应性强、性价比高而被广泛应用于各种高性能伺服系统中。直接转矩控制(以下简称DTC)是一种较成熟的控制策略,无需对被控模型进行解耦计算,具有动态性能较好、鲁棒性好、控制律不复杂等优点[1]。DTC 是将磁链和电磁转矩作为控制变量,利用简单的滞环比较器完成解耦控制,但转矩和磁链脉动大,可调节性差。国内外学者对控制算法进行了研究与改进,其中无差拍控制技术由于其独特的性能,引起了研究人员的关注。无差拍DTC 目标是让转矩和磁链在一个采样周期结束时与给定值的误差为零,具有较快的响应速度,在高速微处理芯片上易于实现[[2];文献[3-5]从理论上可得到电机的磁链和转矩无差控制的最佳参考电压矢量,但增加了复杂性,求解状态变量的计算大,物理意义不明确。文献[6]研究了在电压源逆变器输出电压受限条件下,无差拍DTC 的设计与实现问题。文献[7]为了减小延时并提高伺服系统电流环控制性能,提出了一种基于无差拍控制原理的PMSM 鲁棒预测电流控制算法。文献[8]基于拉格朗日插值的无差拍预测控制算法,提出一种改进无差拍预测控制算法。文献[9]提出一种新型的基于预测算法感应电机无差拍DTC 方法。
以上文献多是研究了异步电机的无差拍DTC方法,从理论上可以推导出转矩和定子磁链控制律,但实际采样周期受限,还不能满足在1 个周期实现误差为零。同时,PMSM 本身的结构、性能与异步电机的区别,因而研究无差拍DTC 在PMSM 系统中的应用有一定的实际意义。本文对空间矢量脉宽调制(SVPWM)的电压矢量计算方法进行改进,采用在一个周期内2 次采样、2 次更新的策略,设计了PMSM在旋转坐标系下的无差拍DTC,以角速度为输入状态变量,并通过扩张观测器获取磁链和转矩的信号,该控制策略具有较好的动态响应,同时能够减小转矩和磁链脉动,提高系统控制的综合性能。
1 PMSM 数学模型
PMSM 在旋转坐标系dq 下的转子磁通定向的电压回路方程如下:

磁链方程:

转矩方程:

式中:p 为微分算子;id,iq和ud,uq分别为电机的d轴和q 轴的电流和电压;Rs为电机的定子电阻;Ld,Lq分别为电机d 轴和q 轴的电感;对凸极式PMSM,存在Ld=Lq=L;ψs为定子磁链;ψf为电机的永磁通;Tem为电机扭矩;p 为电机的极对数;ω 为电机的角速度;B 和J 为电机的粘性摩擦系数和转动惯量。
2 SVPWM 改进设计
2.1 SVPWM 占空比
对于电压型PWM 逆变器,其输出电压空间矢量如图1 所示。下面以扇区2 为例,分析PWM 信号调制和占空比,对于给定电压矢量幅值Um,各个矢量输出矢量时间由式(4)计算:


图1 电压空间矢量分布图
2.2 PWM 更新时序改进策略
对于SVPWM 而言,在每个扇区内电压矢量都不相同,目前在PWM 采样、更新主要有2 种模式,如图2 中模式1 和模式2 所示。

图2 3 种PWM 更新策略对比
本文设计双采样双更新,即在每个周期开始和中间时刻进行本周期的采样时,同时把PWM 更新到上个周期的指令中,故采样PWM 更新算法总共延时时间不会超过0.75Ts。如图2 的模式3 所示,表1 为三种更新模式的延时时间对比。

表1 PWM 更新模式延时时间
3 无差拍直接转矩控制律
3.1 dq 坐标系下的控制律
从定子磁场定向坐标上,可以设想ud控制磁链,而uq控制转矩。无差拍控制[10-13]是在第k 个载波周期 [kTs,(k+1)Ts]开始时刻kTs,采样得到的实际磁链和转矩,计算得到磁链和转矩的偏差Δψf和ΔTem,计算得到参考电压矢量,然后运用SVPWM方法合成输出电压,使得在(k +1)Ts时刻的实际磁链和转矩Tem跟踪参考值和,Δψf=0,ΔTem=0。Ts为采样周期,考虑到数字控制的采样时间足够小,将式(1)转为电流形式后离散化:

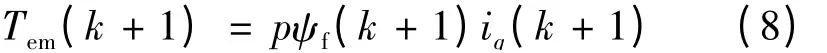

无差拍DTC 的思想就是要求在k +1 时刻的电机转矩等于k 时刻的转矩给定值,即:Tem(k +1)=(k),则相应的q 轴电流在k+1 时刻:

即:

式(9)和式(14)中的ud(k)和uq(k)即是实现无差拍控制所需的电压。
3.2 扩张状态观测器(ESO)估计
在电机运行过程中,电机参数会因发热、磁饱和、dq 轴电流幅值、相角变化而变化,引起误差。因此采用ESO 将所有参数变化对电流id,iq的影响分别用一个附加项表示[15],即:

通过观测补偿这个附加项,可抑制系统参数变化,实现误差矫正,提高系统鲁棒性,ESO 可表示:

式中:z1,z3分别为id,iq观测值;β1,β2,β3和β4为可调参数。在原点附近采用函数fal(e,α,δ)能够消除高频抖震,并实现控制增益随误差的变化而变化,δ为原点附近线性段的区间长度,α1,α2为可调参数,通常在0 到1 之间选择。ESO 只需利用原对象的输入和输出信息进行观测,釆用通用方法设计ESO 的参数β1,β2,β3和β4,保证观测器的稳定性和快速性。将需要观测的部分扩充为fd,fq的观测值z2,z4,将其前馈补偿到式(15)中,可实现对参数变化误差的补偿。
4 系统控制结构图
PMSM 无差拍DTC 结构图如图3 所示,在α-β坐标系下,电机的电压、电流信号和转速信号由传感器测出,定子磁链ψsα,ψsβ,θ 和转矩根据模型由ESO计算得出,然后将磁链、电流转换到两相旋转坐标系下,得到ψsd,ψsq,id,iq,ω 和Tem,再与给定值和比较,得到和ΔTem,再计算实现无差拍控制所需的ud,uq,通过SVPWM 计算出求出完整的空间电压参考矢量后和作用时间,经dq/αβ 转换环节,利用直流母线电压和定子三相电流,计算得出SVPWM所需两相静止坐标系下参考电压矢量uα,uβ,使实际电机转矩达到期望值。在无差拍控制器之前,引入PI 环节实现调节,减少环境对电机参数的影响,降低定子磁链幅值和电压的波动,提高状态量观测的准确性。

图3 PMSM 无差拍DTC
5 仿 真
在MATLAB 中分别建立PMSM 无差拍DTC 和传统DTC 控制系统,PMSM 参数如下:额定功率PN=1.5 kW,额定电压UN=380 V,额定转速nN=3 000 r/min,额定电流IN=3.5 A,极对数p =4,定子电阻RS=2.01 Ω,转子电阻Rr=11 Ω,电感Ldq=0.237 8 mH,J=0.011 kg·m2,ψf=0.8 Wb,逆变器开关频率为10 kHz,观测器参数β1=100,β2=300,β3=800,β4=600,α1=0.5,α2=0.25,系统给定磁链为0.2 Wb。图4 和图5 分别为传统DTC 和无差拍DTC 的定子磁链轨迹图和电磁转矩仿真图。

图4 磁链仿真

图5 转矩仿真
从图4 的磁链仿真轨迹看出,无差拍DTC 减小了磁链脉动,从图5 可以看出,无差拍DTC 有效降低了转矩脉动,提高系统的鲁棒性。图6 为给定转速为1 200 r/min,电动机起动时负载转矩为0,电磁转矩为5 N·m,5 s 突加负载转矩2 N·m 时两种方案系统响应情况对比。
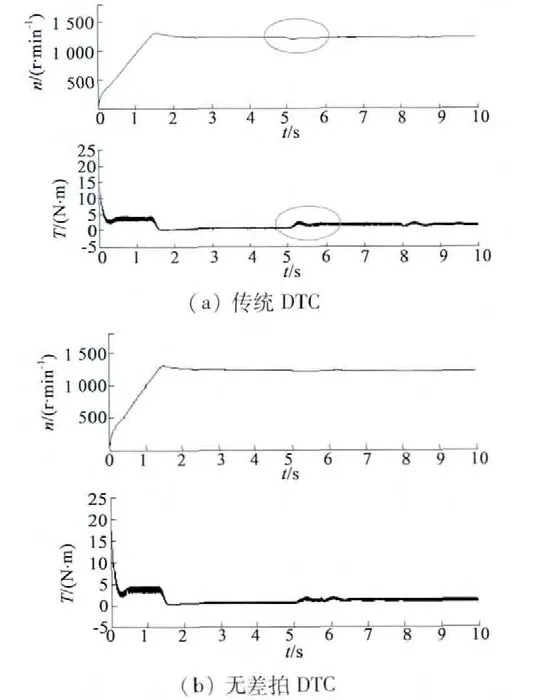
图6 突加负载响应时的转速与转矩对比
从图6 可以看出,无差拍DTC 具有较强的抗负载扰动,在突加负载的情况下,转矩和转速几乎不会发生波动。图7 为传统DTC 和无差拍DTC 的PWM电压信号跟踪仿真图,图8 为两种控制方法下的电压跟踪对比。
从图7 看出,基于传统DTC 算法的PWM 的输出信号和期望值之间有滞后,而无差拍DTC 电压信号只有0.75Ts,几乎无滞后。从图8 看出,无差拍DTC 比传统DTC 快0.5 s。
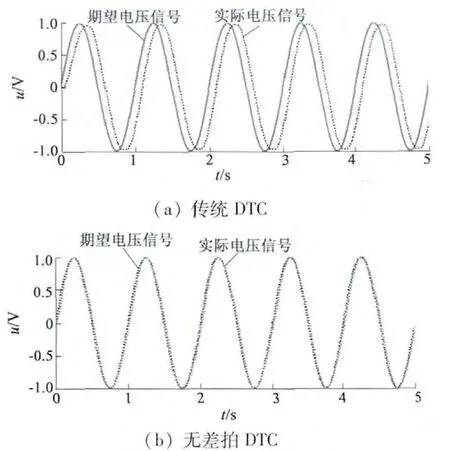
图7 PWM 电压信号

图8 两种方法的电压跟踪对比
6 结 语
本文分析了SVPWM 控制和传统DTC 的优点,针对PMSM 的特点,结合了无差拍和DTC 的优点,提出了PMSM 无差拍DTC 方案。通过分析传统PWM 占空比的不足,提出2 次采样与更新策略,有效地减小了延时。根据PMSM 在旋转坐标系下的数学模型,设计了扩张状态观测器,以定子磁链、转子磁链和角速度为状态变量,以电机参数变化为扰动量,在定子磁链定向坐标系中,理论上推导出PMSM 的无差拍直接转矩电压控制律,仿真实验证明此方法能够降低磁链和转矩的脉动,具有较强的鲁棒性、良好的动静态性能。
[1] 聂晶,张兴华,孙振兴.效率最优的感应电机无差拍直接转矩控制[J].电气传动,2013,10(43):23-27.
[2] 廖永衡,冯晓云,王珍.无差拍空间矢量调制直接转矩控制简化设计[J].电工技术学报,2011,6(6):95-101.
[3] 严殊,肖建.一种无差拍直接转矩控制方法[J].电机与控制学报,2007,11(2):125-129.
[4] WEST N T,LORENZ R D. Implementation and evaluation of a stator and rotor flux linkage-based dead-beat,direct torque control of induction machines at the operational voltage limits[C]//2007 Industry Application Conference,42nd IAS Annual Meeting.2007:690-695.
[5] 王斌,王跃,王兆安.无速度传感器的永磁同步电机无差拍直接转矩控制方法[J].电机与控制学报,2014,6(6):42-49.
[6] 张兴华,孙振兴,沈捷.计及逆变器电压输出限制的感应电机无差拍直接转矩控制[J].中国电机工程学报,2012,7(32):79-85.
[7] 牛里,杨明.基于无差拍控制的永磁同步电机鲁棒电流控制算法研究[J].中国电机工程学报,2013,5(15):80-88.
[8] 郑黎明,毕广明,吴捷.应用SVM 的异步电动机直接转矩控制仿真[J].微特电机,2008,36(5):49-51.
[9] 王晶鑫,姜建国.基于预测算法和变结构的矩阵变换器驱动感应电机无差拍直接转矩控制[J].中国电机工程学报,2010,30(33):65-69.
[10] 刘英培,万健如,梁鹏飞.基于扩展卡尔曼滤波器和空间电压矢量调制的永磁同步电机直接转矩控制[J]. 中国电机工程学报,2009,29(27):67-74.
[11] GUO You-gui,CHEN Cai-xue.Direct torque control system for induction machine fed by space vector modulated matrix converter[J].Control Theory & Applications,2008,4(2):383-388.
[12] 徐艳平,钟彦儒.扇区细分和占空比控制相结合的永磁同步电机直接转矩控制[J].中国电机工程学报,2009,29(3):102-108.
[13] 周扬忠;许海军.直接转矩控制永磁同步发电机相位自校正型定子磁链观测器[J].中国电机工程学报,2012,6(18):98-108.
[14] YANG S M,LEE C H.A deadbeat current controller for field oriented induction motor drives[J].IEEE Transactions on Power Electronics,2002,17(5):772-778.
[15] KENNY B H,LORENZ R D.Stator and rotor-flux-based deadbeat direct torque control of induction machines[J].IEEE Transactions on Industry Application,2003,39(4):1093-1101.

