基于高频波动率估计的中国股市与宏观经济关联性分析
刘 深
一、问题的提出
股票市场作为上市公司向公众筹集资金的主要场所,是经济体动态运行中的重要组成部分。 同时,股票市场还是信息交流的重要平台,各类相关信息在市场参与者的交易中转换为价格变动,而价格变动会直接影响投资者的财富状况, 进而影响他们在市场中的消费行为和投资决策。 所以,股票市场波动可被视为社会情绪和信心的集中体现,与宏观经济存在着千丝万缕的联系。
股市波动与实体经济之间的互动效应一直为学者们所关注。Schwert (1989, 1990)分别研究了20世纪美国大萧条和1987 年股市崩盘事件时发现,重大宏观事件总会导致股市异动, 而在事件过后波动率会回归到与之前相当的水平。 因此,他得出了投机性资产能够更为迅速地对新鲜经济事件作出反应,依据股指波动状态,能预测未来宏观经济走向的结论。 Arestis et al. (2001)在对德国和日本等5 个发达国家数据的实证中指出, 股市规模对长期经济发展指标的作用并不如银行业规模明显, 但他们同时也得到了股市波动与宏观经济有反向作用的结论, 并推测这是由市场不确定性与实体经济间负相关造成的。Bloom et al. (2011)在后来论证了这一结论, 他认为不确定性使市场参与者变得谨慎, 从而导致经济刺激政策生效过程放缓, 对经济周期产生显著的反作用。 类似地,Fornari and Mele (2009)也得出,股市波动作为市场不确定性的度量,对经济周期的预测有促进作用。
不少国内学者也对股票市场与宏观经济的关系进行了讨论。 李冻菊(2006)认为股市规模虽然暂时仍未能发挥对实体经济的促进作用, 但由于股市处在不断发展和完善过程中, 未来依然有可能发挥其晴雨表的价值。 晏艳阳(2004)研究了股指与宏观经济指标间关系,也得到了相似结论。 显然,他们对股市波动与经济形势之间的关系研究不够,周晖(2010)则弥补了这块空缺:他发现上证指数波动与货币政策间联动变化剧烈,但与经济增长间存在着稳定的联动效应,并得出货币政策可以通过调控经济增长来控制股市资产行为的结论。
借鉴国内外学者有益的研究成果, 本文将利用2010 年上证指数1 分钟间隔高频数据,运用高频数据资产价格波动率的稳健估计方法, 分析股指波动与宏观经济之间的关联关系, 考察中国股市作为宏观经济晴雨表的价值。
二、高频数据波动率稳健估计方法
随着资产价格变动信息记录能力的提高,高频数据获取和使用的可能性明显增加。 有学者提出了基于日内收益数据来估算波动率的方法,它有别于以往的GARCH 模型和随机波动模型,对模型不具有依赖性(model-free),而且能够充分利用日内价格的变动信息, 迅速反应出资产价格的波动情况,这类方法被称为已实现波动率估计。 已实现波动率估计是对高频数据波动率的稳健估计方法,其理论思想表现如下:
首先假定资产价格的对数值pt有下列表达形式

其中, 是局部有界的过程,通常称为资产对数价格的均值漂移项(drift),不失一般性,通常假设;是资产的波动项,或称为扩散(diffusion)系数。 (1)式服从以下假设:
假设1: 设资产价格pt是一个连续随机过程,漂移项μt是局部有界的过程, 扩散过程σt右连续有左极限,且局部有界(在任意紧的子区间上具有有限变差)。

参考学者们的普遍做法,不妨设定噪声项服从以下假设:
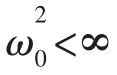
在此条件下,Zhang Lan、Barndorff-Nielsen 和Aït-Sahalia 等学者基于不同角度,分别提出了双尺度(two scale)估计、已实现核(realized kernel)估计和拟极大似然(quasi-likelihood)估计三种可行的稳健估计方法。
1.双尺度估计
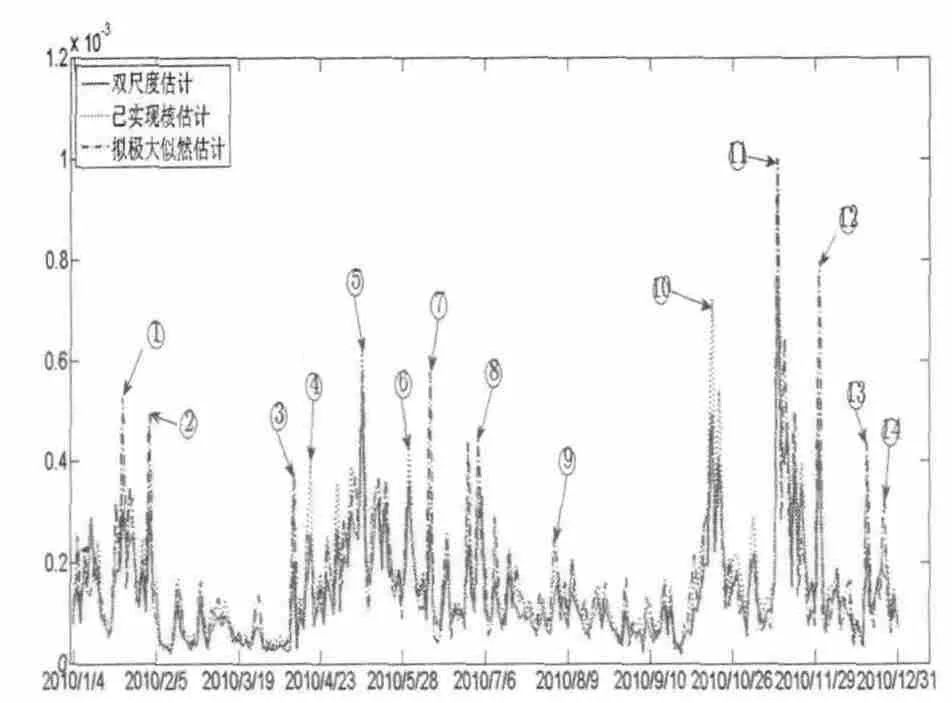
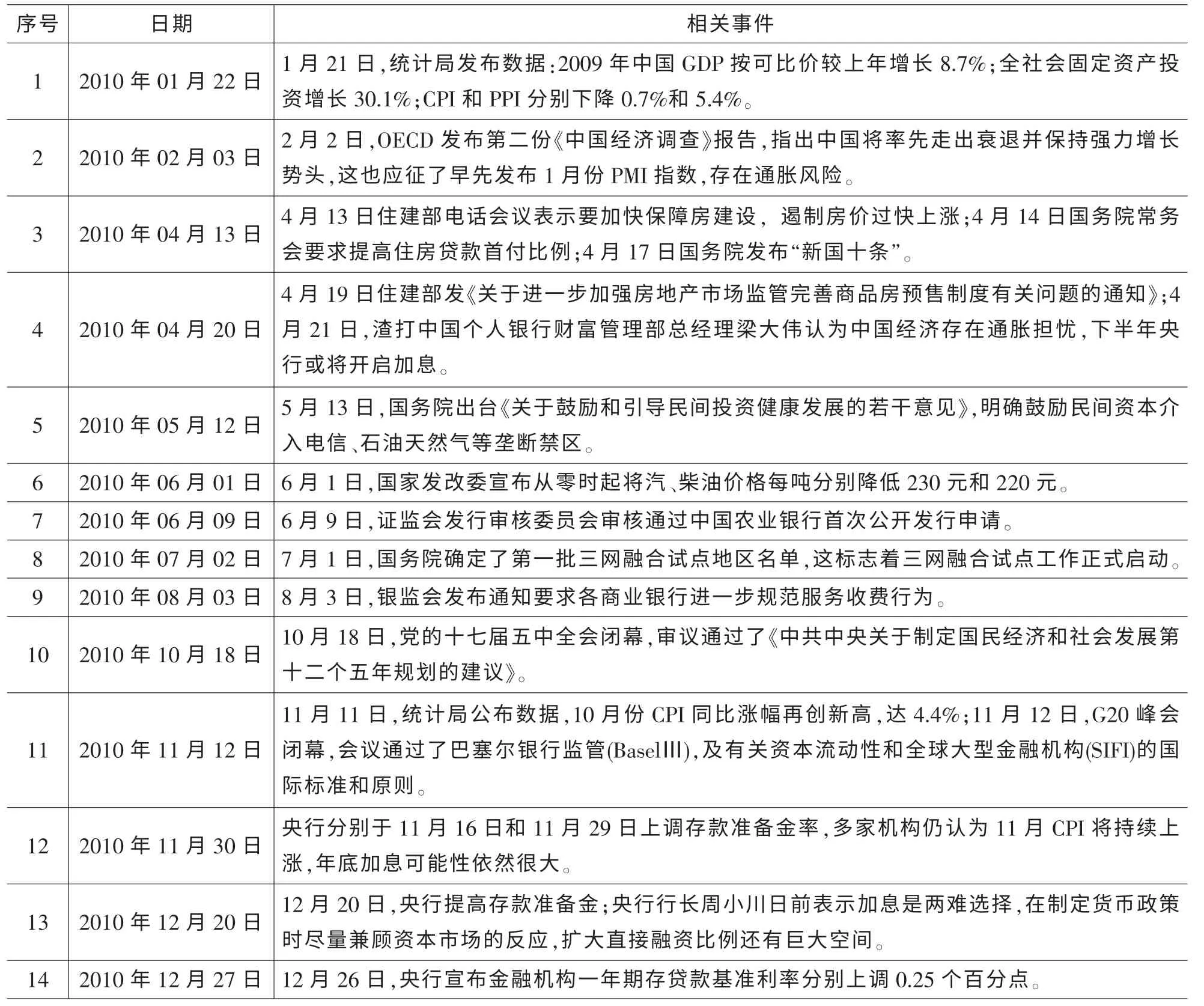
设时间分割点为0=t0 式中,k=1,...,K 决定了第一个样本的起始时间点,K 表示最优时间间隔,而最优样本量[T/K]的确定则是从估计量均方误差的角度出发,使估计量的偏误与方差之和达到最小。 然而,这种做法便意味着要剔除大量的样本,造成信息的流失。 为了能弥补这一缺陷, Zhang et al. (2005)介绍了一种取稀疏子样本估计量平均的方案: 但这种估计方式仍不可避免在估计量中存在的偏差。 Zhang et al. (2005)结合以往成果和平均估计量的优势,提出了一种在噪声干扰下的稳健波动率估计量——双尺度估计量, 其基本形式如下所示: 2.已实现核估计 对于高频价格观测序列p˜t,定义已实现自协方差为: 其中h=-H,...,-1,0,1,...,H, H 是选定的最大滞后阶数; 特别的,h=0 时自协方差正好是传统的已实现波动率估计方法,但这种方法由于受到市场微结构噪声的影响已不再能准确估计资产价格波动率。 Barndorff-Nielsen et al. (2008)利用已实现自协方差期望值中偏差相互抵消的特性,构造出了已实现核估计量: 其中,k(·)是满足(k(0)-1)2+k(1)2=0 的核函数,高阶 的取值则能够有效地帮助控制估计量自身的均方误差。 3.拟极大似然估计 与极大似然法相类似, 拟极大似然法也是一类依赖于分布假定的参数估计方法, 其与极大似然法最大的区别就在于它允许模型设定中存在偏误(miss-specified),这一特性使该方法能够灵活应对更为普遍的问题。 首先来看一个最为简单的情形: 假定dpt=σdBt, 即资产价格的波动项为常数, 噪声项是服从均值为0、 方差为ω2的正态白噪声序列,令参数θ=(σ2,ω2),样本的对数似然函数可以写成: 上述三种稳健估计方法在理论上都具备了较好的收敛性质, 能够稳健应对时间记录点随机、资产价格观测记录中存在有限次跳跃及噪声序列εt存在自相关等情形,高效地估计资产价格波动率,在实践中均得以广泛的应用。 本文也将借助这三种估计方法,研究中国股市与宏观经济之间的关联。 还需要说明的是, 本文所用到的中国股市的高频数据均来源于锐思金融数据库,双尺度估计、已实现核估计和拟极大似然估计三种稳健估计方法的计算都在Matlab 工具包MFEToolbox 中完成。而且, 在估计过程中, 双尺度估计要做小样本修正; 已实现核估计沿用Barndorff-Nielsen et al.(2011) 的定义, 且选择他们所推荐的parzon 核函数, 因为这种只使用日内数据的计算方案较为符合实际情况。 中国股市是在政府强势主导的制度创新与市场自身逐步培育发展条件下共同推进而得以发展壮大的新兴市场(周晖,2010)。 资本市场上股票价格波动不仅是由市场参与者的预期和交易行为造成的,也不仅是由上市公司的财务健康状况和宏观经济的景气程度左右的,更为关键的是受到各类重大经济事件的发生以及市场监管政策与激励政策和货币政策变动等政府宏观调控手段的影响。 图1 是利用双尺度估计、已实现核估计和拟极大似然估计三种方法计算得到的2010 年上证指数波动估计。 根据图1 展示的结果,三种估计方式在上证指数变动问题上持有较为一致的观点:各波动率估计在数值和变动趋势上基本不存在太大区别,因而可以认为计算结果具备一定的可靠性。 图1 2010 年上证指数日波动率 图1 中标注了上证指数波动较为突出的时间点, 并将标注时点附近可能与股指波动相关的宏观经济金融事件列于表1。 从上述图表可以大致看出, 股市的大幅波动背后总是伴随着政策调整等一系列宏观事件的发生。根据本文对标注点新闻整理结果,2010 年造成股市波动的事件大体可分为两类: 1.宏观经济统计数据走弱。四万亿的刺激政策显然让2009 年GDP 的“保八”目标圆满完成,使中国实体经济率先步入复苏进程, 并出现了强势增长的态势。 但由于市场上货币供应量的增加,随之而来的通胀压力却不可小觑。 自2010 年二季度开始,CPI 便一路攀升, 于10 月份和11 月份统计局公布的CPI 同比增长数据相继刷新历史最高记录。 同年,中国的房地产市场也出现了过热发展,由于各类统计数据表现不佳, 促使政府不得不采取手段进行宏观调控。 表1 2010 年上证指数波动相关经济事件 2.宏观经济政策调整。 在2008 年救市政策的刺激下,房地产成交火热:2009 年全国商品房平均售价涨幅约42.18%,35 个大中城市有45.71%涨幅超50%, 2010 年一季度房市仍保持迅猛增长,由此引发中央实施适度从紧的宏观调控政策。 国务院于2010 年4 月17 日颁布了 《国务院关于坚决遏制部分城市房价过快上涨的通知》(简称 “新国十条”), 决心通过宏观调控手段遏制房价的膨胀行为。 “新国十条”,也称为2010 年度中国重大经济事件。 随后商业银行也相继提高贷款利率,收紧了二套房贷。 由于通胀压力日益突出,各大机构纷纷预言央行下半年加息的可能性, 人民银行在2010 年六次上调存款准备金之后, 最终于12 月26 日选择上调存款利率。 事实上,在股票市场中但凡有新的重要信息,必然影响投资者对市场的认知和预期, 改变他们的交易策略,进而导致股票价格发生变动。2010 年正是因为我国政府及时作出宏观调控以及未来政策指向, 再加上国际金融危机引发的市场格局变动等,成为了左右投资者市场预期的重要因素,而这一态度转变则最终集中体现在股市综合指数的波动上,造成股指的上下浮动,这就是股指波动率作为投资者信心状况的综合反应, 与宏观经济事件产生互动的现象, 从中真实地反映出股票市场与宏观经济的密切关联关系。 本文借助高频数据波动率稳健估计理论,论证了上证指数波动与宏观经济事件之间的关联关系,得出几点结论: 一是股指变动综合反映了市场参与者对当前经济状况的认识。 可以把波动率作为股票市场的动态监测指标, 实时监测市场上投资者对宏观经济环境变化所做出的反应, 揭示股指波动率反映市场投资者信心状况的敏感度。 二是股指变动与宏观经济存在关联性。 本文从股指波动与宏观经济事件和主要经济指标间关联两个方面对这一观点进行了实证,2010 年我国一系列宏观经济政策的实施、 政府对市场的调控措施,影响了投资者对市场的认知和预期,左右了他们的交易策略, 进而导致股票市场价格变化与宏观经济事件形成互动,因此,这是股市作为宏观经济晴雨表的价值所在。 三是已实现波动率估计在理论和实践上都有发展空间,特别是在高度强调加强市场监管、防范金融风险的今天, 已实现波动率估计的应用价值和经济价值难以估量, 如何推动该理论的发展和完善, 如何适应各类市场主体和政府监管部门更新更高的要求,是摆在学术界面前的迫切问题。 向理论的深度和广度扩展是必要的, 这就需要决策部门和学术界共同重视这一问题, 为学者们开展已实现波动率估计研究创造良好条件。 最后,不妨借用Schwert (1990)的表述方式,相比显微镜, 上证指数日波动率图1 更像是一张心电图, 它展示了因投资者对未来经济环境不确定而产生的股市风险,反映了金融市场脉搏,并揭示了经济体的综合健康状况。 [1] Arestis, P., Demetriades, P. O., and Luintel, K. B.Financial Development and Economic Growth: The Role of Stock Markets[ J]. Journal of Money, Credit & Banking,2001,(33). [2] Bloom, N., Floetotto, M., Jaimovich, N., Saporta-Eksten,I., and Terry, S. Really Uncertain Business Cycles [ J ].NBER Working Paper 18245, NBER Program,2012. [3] Fornari, F. and Mele, A. Financial Volatility and Economic Activity [ J ]. Discussion Paper 642, Financial Markets Group, London School of Economics and Political Science,2009. [4] Aït-Sahalia, Y., Fan J. and Xiu, D., High-frequency Covariance Estimates with Noisy and Asynchronous Financial Data [ J ]. Journal of the American Statistical Association,2010,(105). [5] Aït-Sahalia, Y., Mykland, P.A., Zhang, L. How often to Sample a Continuous-time Process in the Presence of Market Microstructure Noise [ J].The Review of Financial Studies,2005,(18). [6] Aït-Sahalia, Y., Mykland, P.A., Zhang, L. Ultra high Frequency Volatility Estimation with Dependent Microstructure Noise[ J]. Journal of Econometrics,2011,(160). [7] Barndorff-Nielsen, O. E., Hansen, P. R., Lunde, A.,Shephard, N. Designing Realised Kernels to Measure the Ex-post Variation of Equity Prices in the Presence of Noise [ J]. Econometrica,2008,(76). [8] Barndorff-Nielsen, O. E., Hansen, P. R., Lunde, A.,Shephard, N. Multivariate Realised Kernels: Consistent Positive Semi-definite Estimators of the Covariation of Equity Prices with Noise and Non-synchronous Trading[ J]. Journal of Econometrics,2011,(162). [9] Schwert, G. W. Why does Stock Market Volatility Change over Time? [ J].The Journal of Finance,1989,(44). [10] Schwert, G. W. Stock Volatility and the Crash of '87[ J]. The Review of Financial Studies,1990,(3). [11] Xiu, D. Quasi -maximum Likelihood Estimation of Volatility with high Frequency Data [ J].Journal of Econometrics,2010,(159). [12] Zhang, L. Estimating Covariation Epps Effect, Microstructure Noise[ J].Journal of Econometrics,2011,(160). [13] Zhang, L., Mykland, P.A., Aït-Sahalia, Y. A Tale of two time Scales Determining Integrated Volatility with Noisy High-frequency Data [ J].Journal of the American Statistical Association,2005,(100). [14] 李冻菊.股票市场发展与经济增长的关系研究——源自计量经济学的解释[ J].金融研究,2006,(9). [15] 晏艳阳,李治,许均平.中国股市波动与宏观经济因素波动间的协整关系研究[ J].统计研究,2004,(4). [16] 周晖.货币政策、股票资产价格与经济增长[ J].金融研究,2010,(2).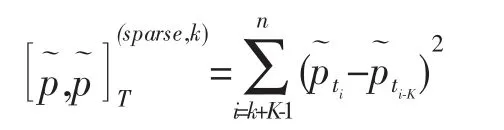
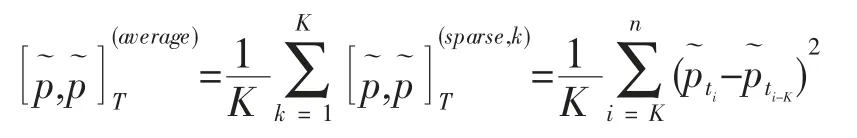
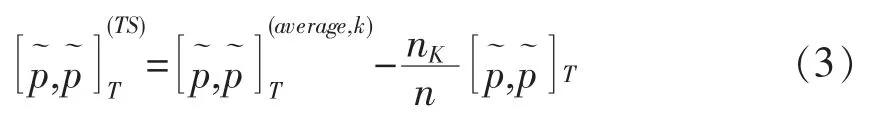
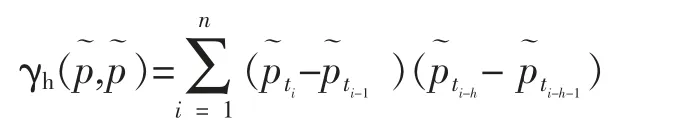
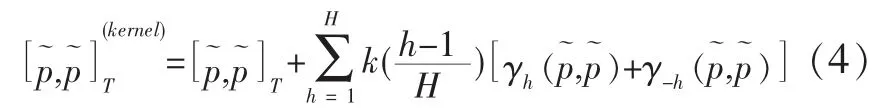
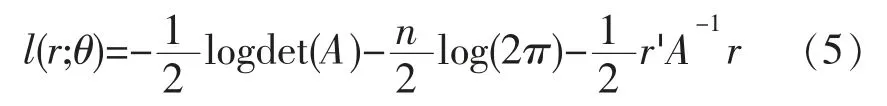
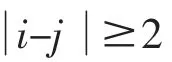
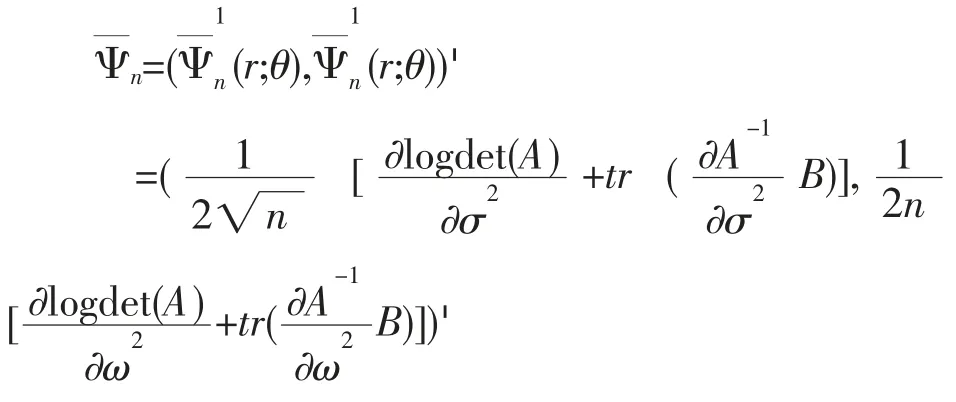
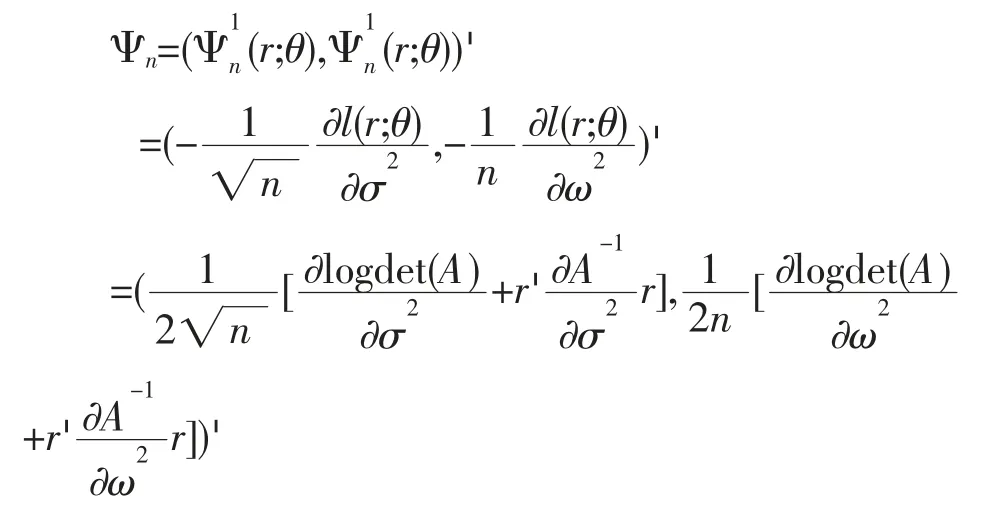
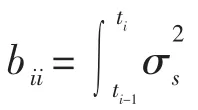

三、在重大经济事件下的上证指数波动实证分析
四、几点结论

