单纯形法中的线性无关性
孙秀华
(安徽建筑大学 数理系,安徽 合肥 230022)
单纯形法作为解决线性规划问题的传统方法,已形成相当成熟的理论,并不断改进简化运算。[1,2]近年来,结合计算机并融合数学建模可更大程度应用运筹学,特别是线性规划中的单纯形法。[3]而单纯形法的原理在于通过迭代不断寻求新的基本可行解,从而得到最优解和目标函数的最优值。基本可行解是指当非基变量全取0 值时,基变量取得非负值而形成的一个解。此时的基变量对应的系数列向量线性无关,并构成线性规划标准型中约束方程组系数矩阵的最高阶的非奇异方阵,即这些列向量为约束方程组系数矩阵所有列向量的最大线性无关组,称为线性规划问题的基。事实上,在单纯形法中,正是其中的线性无关性,才可以保证在每一次迭代中都可以求出非基变量的检验数并确定新的进基变量,进而又要保证确定出基变量后的新的基变量组合仍为基本解,即保证新的基变量对应的系数列向量线性无关。由此可见,线性无关性在单纯形法中有着非常重要的作用。
1 基变量、非基变量与线性无关性
设线性规划问题标准型如下:[4]
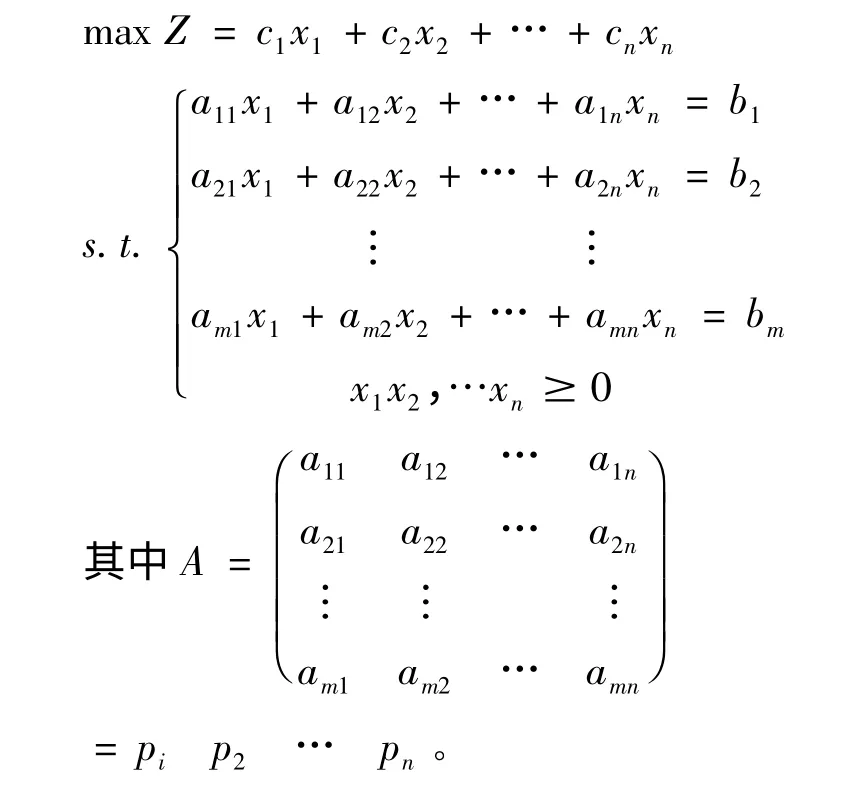
在此不妨假设假设矩阵A 秩为m。
定理1.1[5]设非齐次线性方程组的系数矩阵Am×n的秩R(A)= r,则对应的n 元齐次线性方程组AX = 0 的解集S 的秩Rs= n-r。
由上述定理易得如下命题:
命题1.2 xk1,xk2,…,xkm为第k 步迭代中基变量当且仅当基变量xk1,xk2,…,xkm可由非基变量xkm+1,xkm+2,…,xkn-m表示,即:对1 i m,有xki= b'i-(a'i,m+1xkm+1+ … + a'i,n-mxkn-m)。
证明:“”如果xk1,xk2,…,xkm为基变量,其对应列向量(pk1pk2… pkm)经过初等行变换可化为单位阵,由定理1.1 知xk1,xk2,…,xkm可由自由向量,也即非基变量表示。
“”若对1 i m,有xki都可以由xkm+1,xkm+2,…,xkn-m表示,则xk1,xk2,…,xkm对应列向量(pk1pk2… pkm)可初等行变换为单位阵,即xk1,xk2,…,xkm为基变量。
2 进基变量与线性无关性
由命题1.2 知正因为基变量可以由非基变量表示,每一步迭代时都可以将非基变量代入到目标函数中,同时此时目标函数中不含基变量,进而确定非基变量的检验数,并由检验数的符号确定进基变量。见下例:
例2.1 用单纯形法计算线性规划:
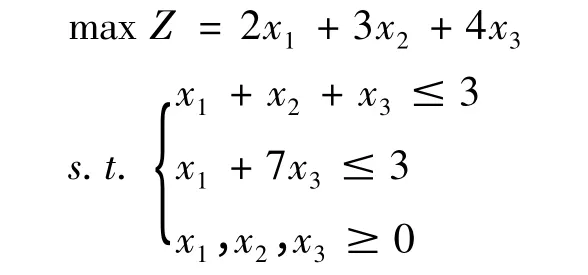
解:引入松弛变量x4,x5将原线性规划问题转化为标准型:
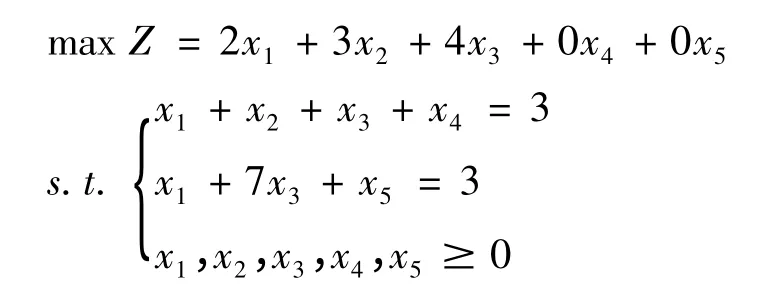
第一步:由(i ≠j)的系数列向量构成单位阵,易知选x4,x5作为基变量,同时非基变量全取0,得基本解(0 0 0 3 9)。
第二步:在约束条件中把基变量用非基变量来
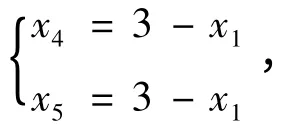
第三步:x1,x5作为新的基变量,得:
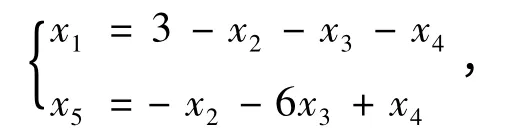
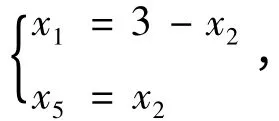
第四步:x2,x5作为新的基变量,得:
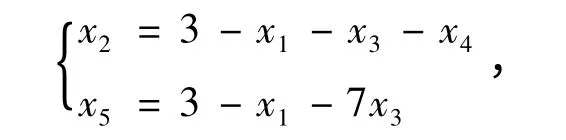
代入目标函数得:Z = 9-x1+x3-3x4,由σ1<0σ3>0σ4<0 故选x3作为进基变量。
再当时,x5= 0,x2=选x5作为出基变量。
而此时x2,x3作为新的基变量,得:
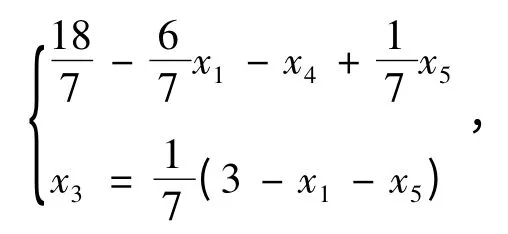
3 出基变量与线性无关性
在确定进基变量后,出基变量的选取便非常重要,这时需要保证两点:新的变量组合是否能保证对应系数列向量线性无关,从而确能构成新的基变量;当非基变量全取0 值,基变量依照约束条件可取得非负值,从而得到的是基本可行解。
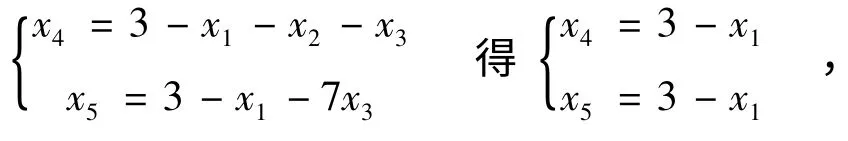
倘若在第二步中选取x2作为进基变量,
此时x2只与x4有关系,而与x5无关,出基变量只能选x4,以使得x2和x5构成新的基变量组合。但显然x2与x4对应的系数列向量线性相关,它们不能成为新的基变量组合。
4 结束语
事实上,在单纯形法的计算中,观察出一个初始的基本可行解后,由上述基变量的线性无关性可知所有的非基变量都可能作为进基变量,但只有通过检验数σk判断出的进基变量xk才可以改善目标函数取值,从而朝最优解方向前进。同样确定了进基得变量后,由前述亦知满足线性无关性和非负约束条件的出基变量可能也并不唯一,通过判断xk所能取得最大值θ,使其它基变量非负,若此时某xt= 0,则xk与xt一定有关系,故可取xt作为出基变量,并且目标函数改善程度最大,达到θσk个单位。
[1]陈利民,苏宏业,牟盛静,等. 基于有界变量单纯形法的区间改进牛顿法[J]. 浙江大学学报(工学版),2003,37(3):269-272.
[2]宋政芳. 单纯形法中进基变量的选择[J]. 上海电力学院学报,2007,23(1):97-99.
[3]邓廷勇,张姮妤. 运筹学教学与数学建模思想的融合[J]. 宜春学院学报,2014,36(9):129-131.
[4]杨民助. 运筹学[M]. 西安:西安交通大学出版社,2000:10-15.
[5]同济大学数学系. 工科数学线性代数[M]. 北京:高等教育出版社,2007:94-102.

