基于样条有限点法的压电功能梯度板的动力分析

黄 君，莫春美，李双蓓，3

(1.桂林理工大学南宁分校 土木与测绘工程系，广西 南宁530001;2.广西大学 土木建筑工程学院，广西 南宁530004;3.广西防灾减灾与工程安全重点实验室，广西 南宁530004)

功能梯度材料(Functionally Graded Materials，简称FGMs)是由两种或两种以上材料组分在特定方向上按一定函数分布而得到的材料。这种近期发展起来的新型复合材料因具有其组分材料的优良特性，并且材料组分间无明显分界，可避免应力集中，广泛应用于对强度和热缓解性能同时有要求的领域［1］。而将FGM 构件与压电材料结合向智能化结构发展是相关领域的主要研究趋势。

目前已有很多关于压电FGM 板振动特性的研究。Behjat 等［2］，Xia 等［3］分别基于有限元法和解析法研究了压电FGM 板几何非线性自由振动问题。黄小林等［4］、Yang 等［5］和Shen 等［6］分别基于Reddy高阶剪切变形理论采用解析法对热环境下压电FGM 板的自由振动和动力响应进行了分析，研究结果表明，热荷载对FGM 板的振动特性影响显著。刘玮等［7］基于经典板理论，采用解析法研究了电场强度和材料组分等对压电FGM 薄板的振动特性的影响。Fakhari 等［8］基于高阶剪切变形理论采用有限元法研究了压电FGM 板在热环境中的非线性自由振动和强迫振动。但目前考虑压电非线性效应影响的研究还较少。Joshi［9］对压电材料的本构关系进行了研究，发现压电材料在强电场作用下表现出电致非线性特性。Kapuria 等［10］考虑电致非线性本构关系，采用有限单元法研究了强电场作用下压电层合板的静力问题。李双蓓等［11-12］基于经典板理论，采用里兹法研究了强电场下的压电层合板弯曲问题，采用样条有限点法研究了强电场作用下压电FGM 板的自由振等动问题，研究表明，强电场作用下电致非线性影响显著不可忽视，而正压电效应的影响微小。由于功能梯度板多应用于热环境下，本文在文献［12］的研究基础上，基于高阶剪切变形理论，考虑热环境对FGM 材料参数影响及温度在压电FGM 板厚度方向的传导问题，并将温差和电场对板自振频率的影响以中面薄膜力形式进行考虑，更深入地探讨强电场作用下的电致非线性效应对压电功能梯度板的动力特性的影响。

1 基本理论

本文研究的是两面贴有等厚压电层的FGM 板，如图1所示。假设压电层与FGM 基层之间的粘结层很薄，其厚度忽略不计。

1.1 材料的热物参数及温度场

假设FGM 板的材料组分沿厚度按幂函数形式连续变化，则与温度相关的物性参数可表示为

其中，P 是与坐标和温度相关的材料参数，包括弹性模量E、密度ρ、热膨胀系数α;下标m、c 分别表示金属和陶瓷材料;若只考虑温度沿板厚方向变化，T=T(z)由热传导方程、热边界条件和边界连续条件共同确定［13］;k 为FGM 板的材料梯度指数;hf为FGM 板的厚度;P0、P-1、P1，P2，P3是与温度有关的系数，由试验得到。本文不考虑热传导系数κ 随温度的变化。由于温度对泊松比μ 的影响很小，设为常数。

图1 压电FGM 板结构及样条离散图Fig.1 The spline discretization model of piezoelectric FGM plate

1.2 本构关系

热环境中考虑热机耦合的FGM 板的本构关系为

压电材料的电致非线性本构方程为［9］

其中，σp为压电层的应力列阵;Cp为压电层的刚度折减后的弹性系数矩阵;为考虑了电致弹性效应和电致伸缩效应的压电非线性项;Dz为电位移;eT=CpdT为压电应力常数矩阵，其中，d是压电应变常数矩阵;e3=Cpd3为电致弹性系数矩阵，其中，d3是电致弹性柔顺系数矩阵;b=Cpm 为电致伸缩系数矢量，其中，m 是电致伸缩柔顺系数矢量;Ez为施加给压电片的电场强度。

1.3 样条有限点法离散化

将压电FGM 板沿x 方向均匀划分进行样条离散化，如图1 所示。采用三次B 样条函数构造压电FMG 板几何中面的位移函数为

采用Reddy 高阶剪切变形理论，板内任意点的位移和应变的样条离散化矩阵表示为:

式中，u1=［u v w θxθy］T为板内任意点的位移和中面转角向量;为应变列阵;N 表示位移形函数;B 是应变形函数。其中，

1.4 热环境中强电场作用下的动力方程

考虑转动惯量影响，板的瞬时总势能泛函表达式参见文献［15］写出。本文忽略正压电效应，则热环境中强电场作用下，将温差和电场产生的薄膜力在中面应变上做的功加入到板的瞬时总势能泛函中，用下式计算:

其中，εN=［w，xw，y］T表示中面应变;NP、NT分别表示电场和温差引起的中面薄膜力，由下式计算:

将功能梯度材料的本构关系式(3)、式(4)和压电材料的本构关系式(6)代入式(19)，并进行样条离散化，得到

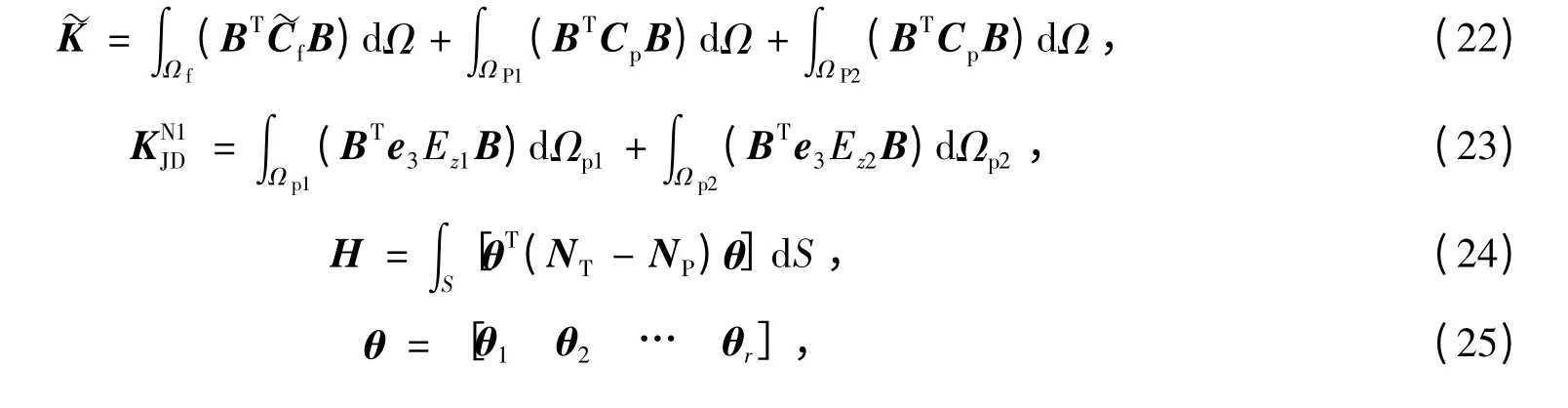
其中，Ωf、ΩP1、ΩP2、Ω 分别表示FGM 层、上下压电层体积及压电FGM 板的总体积;S 为板面面积;mf、mp是密度矩阵;cf、cp为阻尼矩阵;f 为体力为机械面荷载。具体表示式为

其中，ρi为体积密度;Ji表示单位体积转动惯量;ci表示阻尼系数;fx、fy、fz分别为沿x、y、z 方向的体力;分别为沿x、y、z 方向的面力;为绕x、y 方向的力矩。

由瞬时变分原理可得

则不考虑阻尼和外力影响的自由振动方程为

1.5 样条有限点法边界处理

以边界条件为四边固支为例进行说明。四边固支的边界条件如下:

为了满足板y 方向两对边的位移边界条件，振型函数取为

2 数值分析

2.1 验证分析

将本文样条有限点法的线性解与文献［8］的有限单元法的线性解进行对比，板件尺寸及材料参数见文献［8］。四边固支(CCCC)的情况下，分别对比温度变化和电场单独作用时的自振频率λ，结果见表1 所示。频率系数λ 与自振频率ω 的转换表达式为:

表1 给出了3 种情况下样条有限点法和有限单元法的对比结果。第一种是常温且不加电场的情况;第二种是板单面升温不加电场的情况;第三种是常温且两片压电层都加了200V 电压的情况。可见3 种情况下本文解与文献解偏差最大只有1%，吻合得很好，说明本文建立的样条有限点法动力模型正确可靠。从计算收敛情况来看，样条有限点法取N=10，r=2 时就已经收敛，且有较高的精度，此时的自由度是130，而有限元法的自由度是500，可见样条有限点法的计算效率较高。

表1 四边固支压电FGM 板在温度变化和电场作用下的一阶自振频率Tab.1 The natural frequency of fully clamped piezoelectric FGM plate under different thermal and electric conditions

2.2 压电FGM 板自振频率的压电线性解与非线性解的对比分析

本算例取板的长宽a=b=0.6 m，FGM 层厚度hf=3 mm，压电层厚度hp=0.1 mm。FGM 和压电材料参数见表2，其中，FGM 梯度指数k=5。不同边界条件和不同电场下，讨论压电FGM 板的自振频率压电线性解与非线性解的偏差情况。

表2 FGM 和压电材料参数表Tab.2 The material parameters of FGM and piezoelectric material

由图2 知，4 种频率解都随电场增大而增大。其中，四边简支(SSSS)板的频率增大比四边固支(CCCC)板的大，可见，压电FGM 板的边界约束越弱，其自振频率受电场影响越大，也越容易用电场进行振动控制。随电场增大，两种约束形式的线性解与非线性解的偏差都增大，且四边固支边界的偏差要大于四边简支边界，可见，强电场强度作用下采用压电线性本构关系进行计算会产生较大误差，压电材料的电致伸缩效应和电致弹性效应不可忽略，应考虑采用电致非线性本构关系进行计算分析。同时表明压电FGM 板的边界约束越强，电致非线性效应对其自振频率的影响越大。由图2 还可以看到，非线性解曲线都比线性解曲线平缓，可从电致非线性本构关系式(6)解释这一现象。压电线性项eTEz计算中以几何刚度H起作用，由式(24)和式(38)知，电场为负时会减小板的刚度，为正时增大刚度。由计算过程发现，非线性项e3εEz和项的数量级一般很小，可以忽略其影响;e3Ez在计算中起到修正刚度的作用，当电场为负时增大弹性刚度，反之为正时减小板的弹性刚度，且与电场强度Ez成正比关系，电场越大其修正作用越大，与线性项的影响刚好相反。

2.3 振动控制分析

取四边简支的压电FGM 板，板长宽为a=b=0.2 m，FGM 层厚度hf=1.5 mm，压电层厚度hp=0.1 mm，其中，FGM 材料参数同“2.1 节”，压电材料参数见表2。讨论2000 V/mm 的强电场对k=0 的均质板和k=2 的FGM 板自振频率的控制情况，其中的温度环境是板下面为恒温300 K，上面温度变化300 ～310 K。同“2.2 节”，本算例采用频率系数进行讨论。

表3 给出了不同温度环境中电场对均质板和FGM 板的自振频率控制情况。可以看到，随温度升高，均质板和FGM 板的自振频率均有减小，且电场对频率的控制率增大。这是由于温度升高，材料的弹性模量减小，且有温度薄膜力的作用，降低了板的刚度，从而使得频率减小。可见，温度越高，板的弹模越小，越容易通过施加电场对FGM 板进行振动控制。

图2 压电线性和非线性自振频率对比图Fig.2 Compare of linear and nonlinear natural frequencies

表3 强电场对热环境中的压电FGM 板自振频率的控制效果Tab.3 The control effect of strong electric field to the natural frequency of piezoelectricFGM plate in thermal environment

3 结 语

本文基于压电材料的电致非线性本构关系，以薄膜力形式考虑电场和温度产生的纵向力的影响，建立了热环境中强电场作用下压电FGM 板的样条有限点法自由振动分析模型。采用该模型进行算例分析，将样条有限点法的线性解与有限元法的线性解进行对比，验证了本文模型正确可靠。本文方法计算精度好，效率高。对比分析了强电场作用下，在压电本构关系中考虑电致伸缩效应和电致弹性效应与否对板振动特性的影响，结果表明:正电场作用下压电线性解大于非线性解，而负电场下线性解小于非线性解;随着电场增大，线性解与非线性解的偏差增大;边界约束越强，压电非线性效应对板的自振频率的影响越大。最后研究了热环境中强电场对压电FGM 板的振动控制情况，研究发现，温度升高，材料弹模减小，电场控制效果变好。

［1］ 高晓菊，王伯芊，贾平斌，等.功能梯度材料的制备技术及其研发现状［J］.材料导报，2014，28(1):31-36.

［2］ BEHJAT B，KHOSHRAVAN M R.Geometrically nonlinear static and free vibration analysis of functionally graded piezoelectric plates［J］.Composite Structure，2012，94:874-882.

［3］ XIA X K，SHEN H S.Nonlinear vibration and dynamic response of FGM plates with piezoelectric fiber reinforced composite actuators［J］.Composite Structure，2009，90:254-262.

［4］ 黄小林，沈惠申.热环境下功能梯度材料板的自由振动和动力响应［J］.工程力学，2005，22(3):224-227.

［5］ YANG J，SHEN H S.Vibration characteristic and transient response of shear-deformable functionally graded plates in thermal environment［J］.Journal of Sound and Vibration，2002，255(3):579-602.

［6］ SHENH S.Thermal postbuckling behavior of shear deformable FGM plates with temperature-dependent properties［J］.International Journal of Mechanical Sciences，2007，49:466-478.

［7］ 刘玮，闫铂.具有压电元件的功能梯度弹性薄板的振动特性［J］.振动与冲击，2007，26(5):1-3.

［8］ FAKHARI V，OHADI A，YOUSEFIAN P.Nonlinear free and forced vibration behavior of functionally graded plate with piezoelectric layers in thermal environment［J］.Composite Structures，2011，93:2310-2321.

［9］ JOSHI S P.Non-linear constitutive relations for piezoceramic materials［J］.Smart Materials and Structures，1992，1(1):80-83.

［10］KAPURIA S，YASIN M Y.A nonlinear efficient layerwise finite element model for smart piezolaminated composites under strong applied electric field［J］.Smart Materials and Structures，2013，22(5):1-10.

［11］李双蓓，顾春霞，黄 君.强电场作用下压电层合板的非线性弯曲问题研究［J］.广西大学学报:自然科学版，2013，38(6):1284-1291.

［12］李双蓓，黄 君，顾春霞，等.强电场作用下压电FGM 板非线性动力分析的样条有限点法［J］，玻璃钢/复合材料，2014(4):8-12.

［13］黄小林.船舶与海洋工程中复合材料板构件的非线性振动和动力响应［D］.上海交通大学船舶海洋与建筑工程学院，2005.

［14］秦荣.结构力学的样条函数方法［M］.南宁:广西人民出版社，1985.

［15］秦荣.计算结构动力学［M］.桂林:广西师范大学出版社，1997.