部分充填混凝土窄幅钢箱组合梁抗弯承载力

羊海林，莫时旭，郑 艳，李兴科，李 胜

(广西岩土力学与工程重点实验室，广西 桂林541004)

0 引 言

部分充填混凝土窄幅钢箱连续组合梁是在方形钢管混凝土构件和窄幅式钢箱—混凝土组合梁基础上发展起来的一种新型钢箱—混凝土组合梁，主要由钢筋混凝土翼板、填充混凝土的窄幅钢箱梁和剪力连接件三部分组成。其正弯矩区截面与普通钢箱—混凝土组合梁一样，而在负弯矩区的钢箱梁受压部位填充混凝土，从而改善了连续组合梁中支座附件负弯矩区的结构性能，使其受力特点类似方形钢管混凝土偏心受压构件，相比传统空箱—混凝土组合梁同样具有刚度大、自重轻、承载力高等优点，还具有局部稳定性和整体抗扭性能好的特点，处于三向受力状态的混凝土则能更好的发挥抗压性能。同时充填的混凝土对箱梁内锈蚀有良好的防护作用，而且箱内充填混凝土后可以减小应力集中，降低钢箱疲劳的危险等［1-2］。目前，国内外关于类似的钢箱—混凝土组合梁［3-8］的试验研究较少，舒小娟［9］、莫时旭［10］等通过理论与试验研究分析了钢箱—混凝土组合梁的抗弯承载力，并推出了理论计算公式。而部分填充混凝土窄幅钢箱连续组合梁作为一种新型组合结构梁桥形式，其负弯矩区承载能力计算是设计的关键，有必要对其进行更深入研究。结构设计中，一般将结构的极限状态分为两类:承载能力极限状态和正常使用极限状态。因此，对部分填充混凝土窄幅钢箱连续组合梁进行设计时，需对上述两种极限状态下组合梁的抗弯刚度和承载力进行研究。

1 弹性抗弯承载力计算

正常使用阶段的组合梁，其钢箱和纵向钢筋均处于弹性工作阶段。由于混凝土的抗拉强度较小，位于组合梁负弯矩区段的混凝土翼板在受到较小的弯矩作用时即出现微裂缝，因此抗弯承载力计算时一般不考虑其受拉作用。而钢箱内填充的混凝土处于三向受压状态，其压应变处于应力—应变曲线的上升段。因此，对正常使用极限状态下的组合梁研究便可转变为对组合梁弹性工作阶段的研究，即可按弹性理论分析计算。

1.1 截面抗弯刚度与惯性矩

组合梁抗弯刚度的计算是截面抗弯承载力计算的基础，因首先要确定组合梁负弯矩区截面的抗弯刚度。对于连续组合梁而言，中支座负弯矩区段的混凝土翼板处于受拉工作状态，由于混凝土的材料特性在受到较小拉力作用就会开裂，使得连续组合梁的截面刚度沿着梁长度方向不再相同;而负弯矩区钢箱受压部位填充混凝土后，使钢箱腹板的局部屈曲受到约束，屈曲强度大为提高从而使截面抗弯刚度明显变大。由于没有明确的理论计算公式划分正负弯矩区段，本文根据我国现行《钢结构设计规范》(GB50017)取中支座附近0.15L(L 为组合梁单跨跨度)为负弯矩区段，按照截面换算原理计算抗弯刚度，该区段只考虑钢箱、纵向钢筋和钢箱内填充混凝土的抗压作用，忽略翼板混凝土的抗拉作用。正弯矩区段的截面刚度则按照《钢结构设计规范》(GB50017)折减刚度法进行计算，计算公式为:

式中:Ieq为组合梁换算截面惯性矩，按照规范公式计算;ζ 为刚度折减系数，按照规范要求取值;E 为钢材的弹性模量。

由于组合梁负弯矩区的钢筋混凝土翼板与普通钢筋混凝土梁的受拉工作状态类似，可直接引入其参与受拉的程度系数m(0≤m≤1)，在组合梁负弯矩区当翼板未开裂时，混凝土完全参加受拉工作，m=1;随着荷载的增加，混凝土翼板逐渐出现裂缝，并按照曲线形式逐步退出工作(0≤m≤1);当达到弹性抗弯承载力时，混凝土完全开裂退出工作，m=0［11］。综合上述，m 可按下面公式计算:

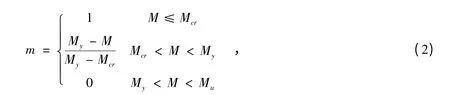
式中:Mcr为开裂弯矩，My为正常使用状态下极限弯矩，Mu为极限弯矩。

每级荷载下组合梁的抗弯刚度均按换算截面原理计算。由于组合梁的混凝土翼板和钢箱填充的混凝土的厚度都比较大，其厚度相对梁高是不可忽略的，为保持换算前后混凝土翼板和填充混凝土的形心位置不变，混凝土翼板和填充混凝土的厚度保持不变，两者的宽度改变，换算后的示意图如图1所示。

根据换算截面法基本原理，将组合梁的混凝土部分全部换算成为钢材，换算后面积为:

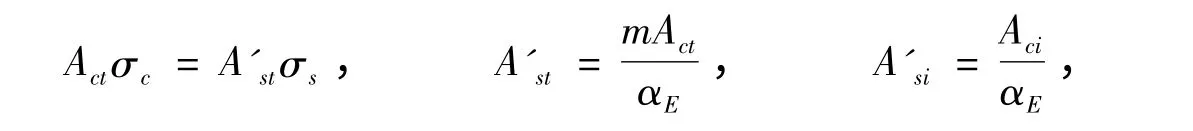
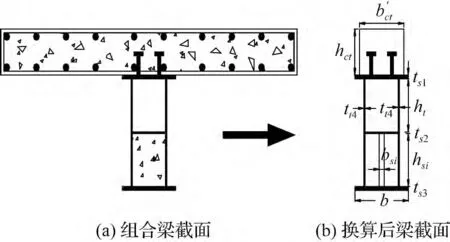
图1 组合截面换算图Fig.1 The section of composite beam conversion

式中:Act、Aci、A'st、A'si、αE分别为翼板截面面积、填充混凝土截面面积、翼板换算后截面面积、填充混凝土换算后截面面积、钢材弹性模量Es与混凝土弹性模量Ec的比值，其中混凝土翼板和填充混凝土换算后的宽度为:b'st=A'st/hst、b'si=A'si/hsi，式中hst、hsi分别为混凝土翼板的厚度和填充的混凝土厚度。

换算截面后，假定组合梁的中性轴位于钢箱内填充混凝土的上部，则梁下缘距中性轴的距离Ys计算式为:

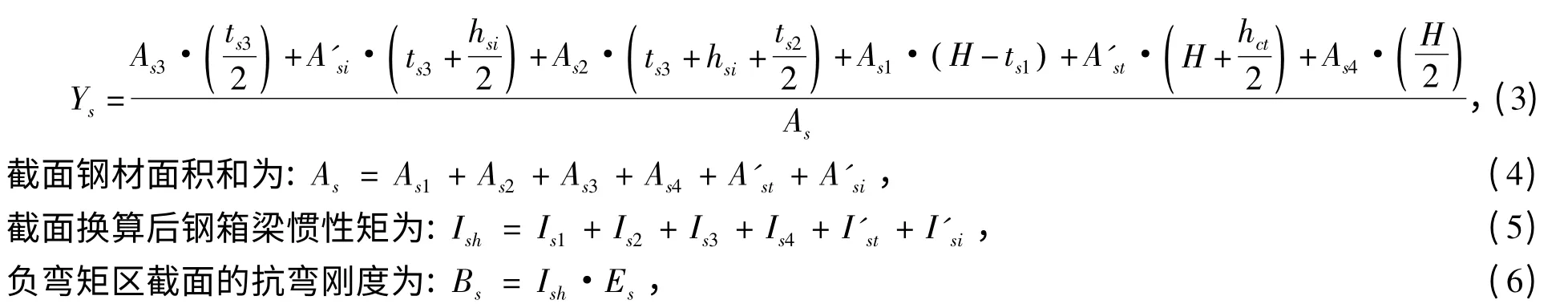
式中:As1、As2、As3、As4、分别为钢箱顶板面积、钢箱中隔板截面面积、钢箱底板截面面积、钢箱腹板截面面积;As为组合梁换算截面后钢材总面积;Is1、Is2、Is3、Is4、I'st、I'si分别为钢箱顶板、钢箱中隔板、钢箱底板、钢箱腹板以及换算截面后的混凝土翼板和填充的混凝土对中性轴的惯性矩。

因此，负弯矩区的截面抗弯刚度按式⑺确定，截面抗弯刚度随荷载的变化过程如图2 所示。

1.2 组合梁的开裂弯矩

荷载作用下，连续组合梁中支座附近为负弯矩区段，混凝土翼板和中性轴上部钢箱处于受拉工作状态，中性轴下部钢箱和填充的混凝土处于受压工作状态。组合梁在开裂前，钢筋混凝土翼板、钢箱内填充的混凝土和钢箱所受的应力值都比较低，截面的应变分布满足平截面假定。由于混凝土的抗拉强度较小，组合梁负弯矩区混凝土翼板上边缘在受到较小荷载作用即出现裂缝，截面抗弯刚度随裂缝的开展逐渐减小，直到混凝土翼板开裂完全退出工作，截面抗弯刚度减小到最小值。因此，负弯矩区截面的抗弯刚度发生变化前所对应的承载能力，即为组合梁的开裂弯矩，其计算公式为:

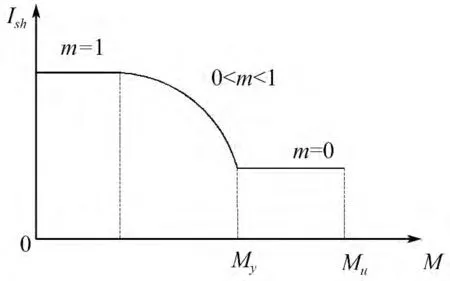
图2 负弯矩区截面刚度随荷载变化过程Fig.2 The relationship between stiffness in negative-moment region and loading

式中，ft为混凝土的抗拉强度，按照文献［12］取为翼板上边缘至换算截面中性轴的距离。

1.3 截面弹性抗弯承载力

部分充填混凝土窄幅钢箱连续组合梁负弯矩区截面的抗弯承载力由钢箱、钢筋混凝土翼板和钢箱内填充的混凝土共同承担，当其中任意材料达到屈服，即可认为组合梁达到弹性极限抗弯承载力。对于非密实截面的连续组合梁负弯矩区而言，由于组合梁在达到弹性承载力极限状态时混凝土翼板已开裂退出工作，对截面发挥作用的为钢箱、纵向钢筋和钢箱内填充的混凝土。因此，组合梁受拉区的纵向钢筋与受压区的钢箱底板都有可能屈服。所以组合梁负弯矩区的弹性承载力极限状态的计算公式有两种情况:

①考虑钢箱底部首先屈服

此时组合梁混凝土翼板的纵向钢筋没有达到屈服应力值，而钢箱梁底板受压达到钢材的屈服强度f'y，其弹性抗弯承载力计算公式:

式中:fy为钢箱底板的屈服强度值，y's为翼板开裂后组合梁换算截面时，底板受力点至换算截面形心的距离，(I'sh=Is1+Is2+Is3+Is4+I'si)为混凝土翼板开裂后换算截面的惯性矩。

②考虑纵向受拉钢筋首先屈服

随着荷载的增加以及翼板上边缘混凝土的开裂，拉应力逐渐转移到纵向钢筋上，当纵向钢筋达到屈服强度fy时，组合梁的弹性抗弯承载力的极限弯矩值My的计算公式:

式中:f'y为纵向钢筋的屈服强度值，y″s为翼板开裂后组合梁换算截面时翼板上缘纵向钢筋受力点至换算截面形心的距离。

2 承载极限状态下的抗弯承载力计算

通常组合梁达到抗弯承载极限状态时，最大弯矩处的钢箱和纵向钢筋大部分均已屈服，填充的混凝土压碎破坏。因此，部分充填混凝土窄幅钢箱组合梁负弯矩区截面抗弯承载力极限值的理论计算方法引入如下假设［13］:

①组合梁在达到弹性极限状态以前，应变满足平截面假定。

②在承载力极限状态，对钢材采用理想弹塑性模型，即截面应力呈矩形分布，混凝土翼板开裂退出工作。

③钢箱内填充的混凝土采用文献［14］提出的偏心荷载作用下方形钢管混凝土构件的本构关系。

④抗剪连接件能充分发挥其塑性变形能力，不考虑其垂直掀起效应。

⑤钢箱与填充的混凝土之间有可靠粘结，忽略两者之间相对滑移;且不考虑混凝土翼板与钢箱之间滑移对承载力的影响。

为简化负弯矩区钢箱内填充混凝土的强度计算，本文仅考虑混凝土压碎后的强度值fc0，且截面应变为矩形分布如图3 所示。根据文献［15］中混凝土的本构关系，取混凝土极限压应变εmax=0.001 5，混凝土强度计算式为:

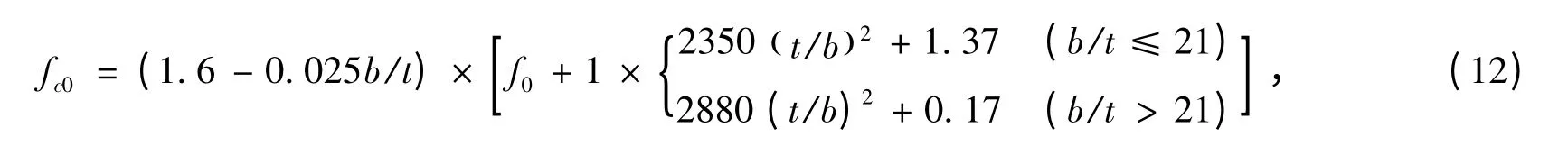
式中:b 为钢箱底板宽度，t 为钢板厚度，f0为混凝土强度值。

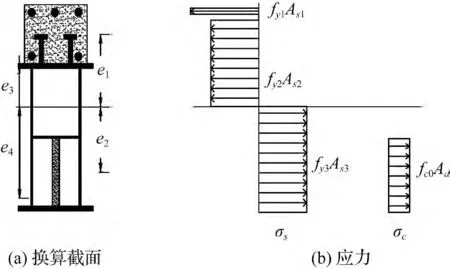
图3 极限抗弯承载力计算模型Fig.3 The computation model of bending capacity in ultimate limit state

根据负弯矩区截面力的平衡关系，则有:

式中:fy1为受拉钢筋的强度设计值，fy2为钢箱的强度设计值，As1为钢筋的截面面积，As2为承载力极限状态下受拉区钢箱梁截面面积，As3为承载力极限状态下受压区钢箱截面面积。

按照弯矩平衡关系，得到组合梁截面抗弯极限承载力计算公式:

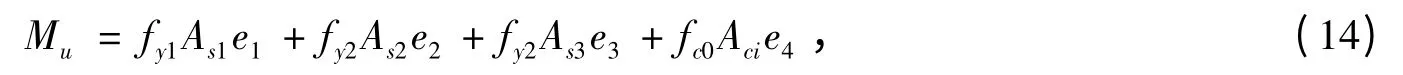
式中:e1、e2、e3、e4分别为受拉钢筋合力作用点、钢箱受压区合力作用点、钢箱受拉区合力作用点及钢箱内填充混凝土合力作用点至中性轴的距离。

3 试验验证

为了验证部分充填混凝土窄幅钢箱混凝土组合梁负弯矩区截面抗弯承载力理论计算式，制作3 根试验简支组合梁(PSCB1-1、PSCB1-2、PSCB1-3)，其中PSCB1-3 试件在加载作用点钢箱腹板内部焊接横向加劲肋，提高加载点腹板的局部抗屈曲能力。加载方式采用正向对称受力，加载点间距1.4 m。各试验组合梁的参数如表1 所示，试验装置与加载装置如图4 所示。钢箱内填充的混凝土强度设计值为C40，对应3 根试验梁的混凝土立方体抗压强度实测平均值分别为fcu1=38.5 MPa，fcu2=39.1 MPa，fcu3=37.7 MPa。钢板型号为Q235，纵向钢筋为HRB335，箍筋为HPB300，钢材的相关力学参数如表2 所示。

表1 组合梁试件材料性参数Tab.1 Main parameters of steel-concrete composite girder

图4 试验装置与加载设备Fig.4 Test device and loading equipment

当加载到60 kN 左右时，相同配筋率的试件PSCB1-2、PSCB1-3 组合梁纯弯段混凝土翼板的上边缘开始出现受拉裂缝，随着荷载的增加，裂缝逐渐由翼板两侧开始向中间延伸。裂缝宽度、长度以及深度也在不断发展。当荷载加到185 kN 左右时，混凝土翼板完全开裂退出工作，纵向钢筋拉应变突增，裂缝宽度也随着快速变大，纵向钢筋和钢箱随荷载增加逐步开始屈服。荷载到达600 kN 左右时，组合梁进入塑性变形阶段，跨中挠度快速增加，负弯矩区达到极限抗弯承载力，钢箱腹板出现局部屈曲，组合梁无法继续承载，试件受弯破坏。试验数据经处理分析后，得出PSCB1-1、PSCB1-2 和PSCB1-3 试件负弯矩区截面纵向钢筋和钢箱梁底板的荷载—平均应变关系曲线(如图5 所示)。图5 中，右边纵向钢筋的曲线从开始施加荷载到荷载—应变曲线的首次转折，曲线上升段近似直线，此时负弯矩区处于弹性工作阶段;首次转折点表示混凝土翼板开裂完全退出工作，纵向钢筋承受大部分的拉应力。若钢筋先屈服，此时纵向钢筋荷载—应变曲线的峰值对应负弯矩区截面抗弯承载力极限值，即组合梁发生弯曲破坏。

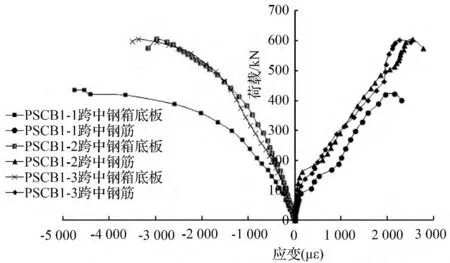
图5 荷载—应变曲线Fig.5 The curves of load-strain

若钢箱底板先发生屈服，从图5 左边钢箱底板的荷载—应变曲线可以看出，随着荷载的增加，荷载—应变曲线斜率逐渐增大并出现转折，钢箱底板由弹性工作阶段进入塑性工作阶段，即组合梁负弯矩区截面达到弹性抗弯承载力极限值。由于钢箱内填充混凝土的箍套作用提高了钢箱梁截面的整体刚度，因此腹板局部屈曲并不非常明显。图6 为PSCB1-2 组合梁达到承载力极限值发生弯曲破坏，钢梁腹板局部屈曲，从图6 中可以看出完全卸载后组合梁仍具有较大的残余挠度。

图6 PSCB1－2 组合梁弯曲破坏图Fig.6 PSCB1-2 bending failure diagram of composite beam

4 理论计算值与试验实测值对比

由理论计算分析得出，组合梁混凝土翼板开裂前后其截面中性轴一直位于填充混凝土的上部，PSCB1-1 试件纵向钢筋先于钢箱底板屈服，而PSCB1-2、PSCB1-3 试件钢箱底板先于纵向钢筋屈服。分别按上述理论推导相应的公式求得开裂弯矩、弹性抗弯承载力My 和极限抗弯承载力Mu 与实测值进行对比(表3 所示)，不计界面处相对滑移对抗弯承载力的影响。从表3 中数据可以看出，PSCB1-1、PSCB1-2 和PSCB1-3 试件开裂弯矩理论计算结果与实测结果比值分别为1.20、1.14 和1.12 相差较大，分析其原因是翼板浇筑时混凝土塌落度过大，组合梁翼板上表面浮浆层过厚，导致理论计算开裂弯矩与实测值出现较大偏差;PSCB1-1、PSCB1-2 和PSCB1-3 试件的混凝土翼板弹性抗弯承载力比值分别为1.03、1.05 和1.05，说明理论计算值与试验值较好吻合;而极限抗弯承载力PSCB1-2 和PSCB1-3 试件计算值与实测值比值为1.09 和1.10 相差较小，PSCB1-1 试件偏差较大是由于钢箱内充填的混凝土振捣不够密实，混凝土实际抗压强度小于设计值，使得充填的混凝土没有起到约束钢箱腹板结构变形的效果，导致极限抗弯承载力比值相差达到1.25。由于剪力连接程度对负弯矩区抗弯承载力的影响关系没有在计算公式中得到体现，所以PSCB1-3 的承载力计算值较PSCB1-2 的安全度小。

表3 抗弯承载力计算值与试验值比较1Tab.3 The compare between test value and calculated value about bending capacity

5 结 论

部分充填混凝土窄幅钢箱试验梁在弯曲破坏后表现出良好的结构延性和较高的强度储备等塑性特征。相比文献［14］传统型空箱—混凝土组合梁，由于负弯矩区钢箱受压部位填充混凝土的存在，使得钢箱腹板和底板变形只能为向外凸，延迟了组合梁局部屈曲的发生，提高了钢箱的局部稳定性，同时由于限制了结构变形使得组合梁的抗弯承载力极限值得到提高。

通过试验结果与理论计算结果的对比分析，得出如下结论:

①PSCB1-1 组合梁理论计算结果偏大主要原因是钢箱内充填的混凝土不够密实，填充混凝土的箍套效应不明显，导致钢箱腹板过早屈曲降低了抗弯承载力。PSCB1-2 和PSCB1-3 组合梁由于混凝土翼板配筋量的提高，荷载到达极限承载力时钢箱顶板并没完全达到屈服强度，使得按简化塑性理论计算的结果偏大。

②试验结果对比可以看出，连续组合梁剪力连接件间距的变化对负弯矩区截面抗弯承载力的影响不明显。而配筋率的不同对非密实截面组合梁负弯矩区的抗弯承载力和混凝土翼板裂缝发展的影响很明显，增加配筋率能明显的提高组合梁的抗弯极限承载力，配筋率的提高同时能有效的控制混凝土翼板裂缝宽度。

③根据混凝土翼板的参与受拉工作状态的程度系数m，按换算截面原理确定连续组合梁负弯矩区截面的惯性矩与抗弯刚度，求出截面的开裂弯矩和弹性抗弯承载力，并根据简化塑性理论推导出截面极限抗弯承载力计算式，试件PSCB1-1 由于钢箱内充填的混凝土不够密实，导致理论计算值与试验结果比值为1.25 偏差较大，而试件PSCB1-2 和PSCB1-3 的理论计算结果与试验结果比值分别是1.09 和1.10 较好吻合，具有一定的工程精度，可以用于设计参考。

［1］ 莫时旭，郑艳，钟新谷，等.钢箱—混凝土组合梁受力性能有限元分析［J］.广西大学学报:自然科学版，2010，35(4):543-548.

［2］ 刘滔，舒小娟，沈明燕.钢箱—混凝土组合梁极限扭矩分析［J］.铁道科学与工程学报，2012，9(2):43-47.

［3］ 尧国皇，林松，陈宜言.钢箱—混凝土组合梁抗弯力学性能研究［J］.特种结构，2010，27(2):10-13.

［4］ NAKAMURA S，MORISHITA H.Bending strength of concrete-filled narrow-width steel box girder［J］.Journal of Constructional Steel Research，2008，64(1):128-133.

［5］ RYU H K，CHANG S P，KIM Y J，et al.Crack control of a steel and concrete composite plate girder with prefabricated slabs under hogging moments［J］.Eng Struct，2008，27(11):1613-1624.

［6］ 舒小娟，钟新谷，沈明燕，等.钢箱—混凝土组合梁初步设计与应用［J］.土木工程学报，2011，44(增刊):8-16.

［7］ 张南，洪英维.体外索钢箱—混凝土组合梁力学性能研究［J］.土木工程学报，2007，39(12):60-66.

［8］ 聂建国，陶慕轩.预应力钢—混凝土连续组合梁的承载力分析［J］.土木工程学报，2009，42(4):38-47.

［9］ 舒小娟，钟新谷，沈明燕.钢箱—混凝土组合梁抗弯承载力理论与试验研究对比分析［J］.铁道科学与工程学报，2006，2(6):19-26.

［10］莫时旭，钟新谷，郑艳，等.钢箱—混凝土组合梁力学性能分析与试验研究［J］.哈尔滨商业大学学报:自然科学版，2008，23(6):707-713.

［11］胡少伟，叶祥飞.预应力连续组合梁负弯矩区抗弯承载力分析［J］.工程力学，2013，30(11):160-165.

［12］周安，戴航，刘其伟.钢箱—预应力混凝土组合梁负弯矩区结构性能试验研究［J］.土木工程学报，2009，42(12):69-75.

［13］钟新谷，舒小娟，沈明燕，等.钢箱—混凝土组合梁正截面强度设计理论与试验研究［J］.中国工程科学，2008，10(10):47-53.

［14］李四平，霍达，王箐，等.偏心受压方钢管混凝土柱极限承载力的计算［J］.建筑结构学报，1998，19(1):41-51.

［15］莫时旭，钟新谷，舒小娟，等.钢箱—混凝土组合梁试验研究与承载能力计算［J］.工业建筑，2006，36(增刊):499-503.