L 形偏心框架结构混合减震分析

段绍伟，毛 轴，陈 敏，贺国京

(中南林业科技大学 土木工程与力学学院，湖南 长沙410004)

鉴于建筑使用功能的要求，框架结构因能形成大的空间得到了广泛应用。《高层建筑混凝土结构技术规程》规定，抗震设计的混凝土高层建筑，其平面布置宜简单、规则、对称、减少偏心，但在场地受限和建筑要求的情况下，不可避免会形成平面不规则框架结构。大量震害显示［1-4］，平面不规则的偏心结构不仅会发生平面和竖向振动，还会发生扭转振动，而扭转反应是造成结构抗震性能退化并导致结构破坏甚至倒塌的重要原因。国内外学者对结构消能减震做了大量研究，文献［5-10］中对粘滞阻尼器的减震设计方法及相关参数进行了研究;文献［11-13］中对结构的耗能减震与防屈曲支撑钢框架设计理论进行了探讨。《高层建筑混凝土结构技术规程》对偏心结构的扭转周期比、位移比、层间位移角等指标均有规定的限值。L 形偏心框架在地震作用下存在明显的扭转效应，若仅在结构中设置粘滞阻尼器，虽能满足小大震作用下规范对层间位移角的要求，但由于粘滞阻尼器并不能给结构附加刚度，因而周期比、位移比很难满足规范要求;若仅在结构中设置屈曲约束支撑，抗侧刚度的增加使结构的地震响应也随之增大。本研究发现，仅采用屈曲约束支撑的结构在小震作用下并不能确保层间位移角小于规范限值，但楼层剪力较原结构有较大幅度的提高。为此，本研究运用屈曲约束支撑与粘滞阻尼器混合减震［14-15］的方法，研究L 形偏心框架结构的动力性能。

1 理论模型及运动方程

1.1 偏心结构理论模型

在一般的结构抗震分析中，通常将结构简化成平面模型，分别在其两个主轴方向进行计算，但这种分析方法仅适用于质量中心与刚度中心重合的规则结构，而偏心结构中的质量中心与刚度中心往往存在偏心，地震时作用在质量中心的惯性力将对结构刚度中心产生扭转力矩，迫使结构产生扭转耦联的空间振动。因此，对结构采用以下假定:①在振动计算中，各层质量都集中于楼板平面内;②不考虑楼板的变形，即认为楼板在其平面内无限刚;③忽略柱的轴向变形，楼板只产生水平方向的位移。通过上述假定即可得到如图1所示的串联刚片模型。

1.2 平扭耦联结构运动方程及阻尼比的计算

由串联刚片模型得，偏心结构的运动方程为:

式中，M 为结构的质量矩阵，K 为混合减震结构的刚度矩阵，C 为混合减震结构的阻尼矩阵，分别为运动方向上的位移、速度、加速度，为地面运动加速度，Ks是无控结构的刚度矩阵，Ke是屈曲约束支撑、粘滞阻尼器的等效水平刚度矩阵，Cs是无控结构的阻尼矩阵，Ce是屈曲约束支撑、粘滞阻尼器的附加阻尼矩阵。由于粘滞阻尼器不提供刚度，Ke可由屈曲约束支撑芯材强度和横截面积得到，关键在于计算附加阻尼矩阵Ce。

计算阻尼矩阵时，可取瑞雷阻尼矩阵［16］，即:

为计算α、β，利用模态分析所得到的前两阶圆频率及阻尼比，有

联立式(4)、(5)求解可得:

式(6)中，ω1、ω2和ξ1、ξ2分别为结构前两阶振型的基本圆频率和阻尼比。结构阻尼比包含两部分，即结构自身阻尼比和消能装置提供的附加阻尼比，根据结构的质量矩阵M、总刚度矩阵Ks+Ke可求得其频率向量和振型矩阵，即:

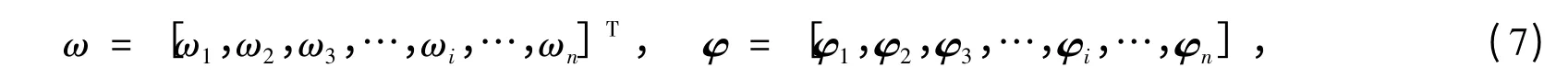
其中，ωi、φi分别为混合减震结构第i 阶振型频率和特征向量。按照振型分解法，将多自由度体系转化为广义单自由度体系:

由于消能装置附加阻尼矩阵Ce通常不满足正交条件，近似处理时，忽略Ce中的非正交项，即:

考虑结构的平扭耦联作用，解耦后可写成:

式(11)、(12)中，γj为振型参与系数，ζj为混合减震第j 振型总阻尼比，ζsj、ζej分别为第j 振型结构自身阻尼比和消能装置提供的附加阻尼比。

2 工程算例分析

2.1 工程概况

某国家重点工程实验室为钢筋混凝土框架结构，混凝土强度等级C30，第一层层高4.5 m，第二层～第十层层高3.3 m。梁截面尺寸250 mm×600 mm，柱截面尺寸600 mm×600 mm，板厚100 mm。梁柱纵向受力钢筋采用HRB400 级钢筋，箍筋与板中受力钢筋采用HRB335 级钢筋。屈曲约束支撑采用十字形内芯，Q235 钢材，内芯面积As=1 968 mm2，外围约束单元由混凝土与方钢管套筒组成。粘滞阻尼器参数:最大行程±50 mm，设计阻尼力800 kN，设计速度540 mm/s，阻尼系数800 kN/(mm·s-1)，阻尼指数0.15。抗震设防烈度为8 度，设计基本地震加速度为0.20 g，采用《建筑抗震设计规范》规定时程分析时的峰值加速度，即多遇地震取70 cm/s2，罕遇地震取400 cm/s2。地震分组为第一组，场地类别Ⅱ类，抗震设防为标准设防类，安全等级二级，平面布置如图2 所示。

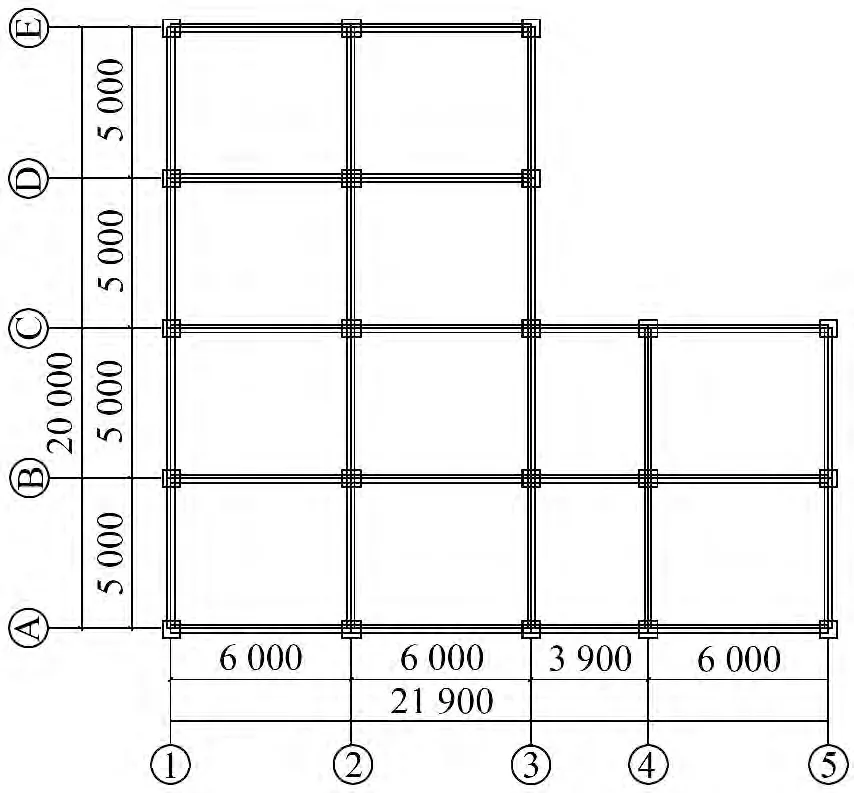
图2 平面布置图Fig.2 Layout of the floor

2.2 有限元模型

在Midas Gen 软件中建立模型并对结构进行非线性时程分析，模型中梁柱结构采用梁单元，楼板采用板单元，屈曲约束支撑采用人字形，粘滞阻尼器采用单斜布置方式。屈曲约束支撑小震作用下处于弹性状态，并不能够消能减震，但它给结构增加了一定的侧向刚度，故用普通梁单元来模拟，截面面积与芯材面积相同，仅需释放梁端部约束;大震分析时，屈曲约束支撑屈服耗能，用一般连接中的滞后系统来模拟。粘滞阻尼器小、大震分析时均采用一般连接中的粘弹性阻尼器来模拟，结构三维模型如图3 所示。

2.3 结构地震响应时程分析

2.3.1 多遇地震下弹性时程分析

根据结构自振周期、场地土类别选取El-centro 波、Taft 波和1 条人工波进行动力时程分析，3 条地震波持续时间均为15 s。由于粘滞阻尼器(Viscous Damper)仅提供阻尼，不提供侧向刚度，当偏心结构中仅设置粘滞阻尼器时，几乎不能减小结构的扭转位移比及扭转周期比，或者需要大量布置粘滞阻尼器才能达到满意的减震效果，且粘滞阻尼器的价格较屈曲约束支撑高，因此，在达到相同减震效果时，应尽量多的选择布置屈曲约束支撑。本文对原结构(无控)、设置屈曲约束支撑结构(BRB)、设置屈曲约束支撑和粘滞阻尼器结构(BRB+Viscous Damper)的各项参数指标进行对比分析。

①扭转周期比、扭转位移比

屈曲约束支撑的布置位置如图4 所示。方案1:BRB 布置在椭圆位置;方案2:BRB 布置在圆位置;方案3:BRB 布置在矩形位置;方案1、2、3 均为1 ～10 层连续布置，方案4:1 层BRB 布置在矩形位置，2 ～10层BRB 布置在椭圆位置。

图3 三维模型Fig.3 Three-dimensional model

图4 BRB 及粘滞阻尼器平面布置图Fig.4 Layout of BRBs and viscous dampers arrangement

表1 和表2 为Midas Gen 有限元软件计算的4 种方案的扭转周期比、扭转位移比。从表1 中可看出，无控结构的扭转周期比为0.922 4 ＞0.9，不满足规范要求，布置屈曲约束支撑后，4 种方案的扭转周期比均小于0.9，由方案1 ～4 中扭转周期比的变化不难发现，屈曲约束支撑越远离结构的刚度中心，即屈曲约束支撑布置在结构的端部，如方案1 所示，其提供的抗扭刚度越大，扭转周期比越小，若仅从周期比方面考虑，应选择方案1 的布置方式。

表2 中无控结构的位移比均超过规范限值1.2，方案1 中，第三层至屋顶位移比均减小，由于层高的影响，此时第二层的扭转位移比为1.279 5，较原结构有增大趋势，且超过了规范限值1.2;方案2 中第三层～第十层的扭转位移比均超过规范限值1.2，而第二层的扭转位移较方案1 的有减小的趋势;方案3 中第三层～第十层的扭转位移比较原结构均有所增大，第二层位移比仍小于规范限值1.2。经综合考虑与软件试算，最终确定BRB 的优化布置方案为方案4，其扭转周期比、位移比见表1 和表2，均小于规范限值。

表1 扭转周期比Tab.1 The ratio of torsion period to translation period

表2 扭转位移比Tab.2 Torsional displacement ratio

②层间位移角

陈敏等［8］对阻尼器在框架结构中的优化布置进行了研究，表明在框架底部两层或者三层安装粘滞阻尼器即可取得满意的减震效果，使之满足规范的要求。本工程在1 ～3 层安装粘滞阻尼器，具体位置如图4，三角形位置为粘滞阻尼器的平面布置位置。

图5 ～图7 为各地震波分别沿X 向，Y 向输入时的层间位移角。由图可知，无控结构在3 种地震波作用下均有楼层层间位移角超过规范限值1/550，而采用BRB 优化布置方案4 后，图6、图7 的层间位移角均小于1/550，而图5 中的层间位移角较无控结构反而增大，超出了规范限值。研究结果表明:结构中设置BRB 后，随着支撑面积的加大，整体结构抗侧刚度增强，在水平地震作用下，框架的侧移有减小的趋势;与此同时，整体结构的刚度增大后，作用于结构的地震力也随之增强，框架的水平侧移有增大的趋势。因此，结构中设置BRB 后，其层间位移角变化并不呈现出规律性，而是表现出随机性。采用BRB+粘滞阻尼器混合减震后，不仅能使周期比、位移比满足规范，且能大幅度减小结构的层间位移角，将其控制在规范允许的范围内，减小幅值最大达50%，减震效果显著。

图5 El-Centro 波沿X 向、Y 向输入时的层间位移角Fig.5 The story drift of structure under El-Centro ground motion in X direction，Y direction

图6 Taft 波沿X 向、Y 向输入时的层间位移角Fig.6 The story drift of structure under Taft ground motion in X direction，Y direction

图7 人工波沿X 向、Y 向输入时的层间位移角Fig.7 The story drift of structure under artificial wave in X direction，Y direction

③层剪力最大值

图8 为El-Centro 波沿X 向、Y 向输入时，各楼层剪力最大值。从图8 中可看出，无控结构的剪力值较小，设置BRB 后，剪力值大幅度提高，增幅最大达155%，验证了地震力随着结构抗侧刚度的增加而增大，如果增加BRB 的数量，则又回到了传统抗震设计思维“以硬碰硬”的老路中。采用屈曲约束支撑与粘滞阻尼器混合减震后，层剪力值大幅降低，接近无控结构的层剪力值。这不仅提高了结构整体的抗侧刚度，且由于其层剪力的增幅较无控结构的增幅并不大，抗侧构件数量的增加减小了框架柱承受的剪力，从而提高框架柱的安全储备。

图8 El-Centro 波沿X 向、Y 向输入时的层剪力最大值Fig.8 The maximum story shear of structure under El-Centro ground motion in X direction，Y direction

2.3.2 罕遇地震下弹塑性时程分析验算

仍然选取2 条天然波El-Centro 波、Taft 波和1 条人工波对混合减震结构(BRB+Viscous Damper)进行大震验算。弹塑性时程分析时，梁柱构件均采用塑性铰模型，非弹性铰特性值采用程序提供的修正武田三折线模型，分析结果如图9 所示。由图9 可见，大震下层间位移角最大值为1/54，小于规范规定的钢筋混凝土框架结构弹塑性层间位移角限值1/50，故能满足抗震规范三水准中“大震不倒”的要求。

图9 弹塑性层间位移角Fig.9 The elastic-plastic story drift

3 结 论

本文采用串联刚片模型，建立了平扭耦联结构的动力方程。对1 栋10 层钢筋混凝土L 形偏心框架结构在无控、设置屈曲约束支撑、联合运用屈曲约束支撑与粘滞阻尼器的减震效果进行了对比分析，研究结果表明:

①通过优化布置，屈曲约束支撑能有效地降低L 形偏心框架结构的扭转周期比、位移比、并将其控制在规范允许的范围内，从而减小偏心框架结构的扭转效应;屈曲约束支撑位置越远离结构的刚度中心，周期比越小。

②粘滞阻尼器在小大震作用下均能起到消能减震的作用，且耗能能力强，在结构底部3 层安装粘滞阻尼器即能较好地控制结构的层间位移角，减小楼层剪力。

③在L 形偏心框架结构中，综合运用屈曲约束支撑与粘滞阻尼器对L 形偏心框架结构进行混合减震，使结构的扭转周期比、位移比等参数均能满足规范要求，弥补了传统减震方法中仅用单一消能器减震的不足，混合减震中两种消能器的优点都得到了充分发挥，减震效果明显。

［1］ MINORU W.Design of earthquake-resistant buildings［M］.New York:McCraw-Hill Company，1986:92-93.

［2］ MELI R.The 1985 earthquake:causes and effects in Mexico City［J］.Concrete Int，1986，8(5):23-34.

［3］ TSAI K C，HSIAO C P.Overview of building damage in 921 Chi-chi Earthquake［J］.Earthquake Engineering and Engineering Seismology，2000，2(1):93-108.

［4］ 吴晓云，陈森，魏琏.论地震作用下多层平扭耦联建筑的刚心［J］.地震工程与工程振动，1998，8(4):33-44.

［5］ 李创第，刘伟，葛新广，等.带支撑分数导数粘滞阻尼器减震结构随即响应［J］.广西大学学报:自然科学版，2010，36(1):28-32.

［6］ 周云.粘滞阻尼减震结构设计［M］.武汉:武汉理工大学出版社，2006.

［7］ 刘鹏飞，刘伟庆，王曙光，等.非线性粘滞阻尼减震结构基于位移的设计方法［J］.世界地震工程，2009，25(4):167-173.

［8］ 陈敏，贺国京.阻尼器在框架结构中的优化布置策略［J］.土木建筑与环境工程，2013，35(4):21-27.

［9］ CHANG K，LIN Y，CHEN C.Shaking table study on displacement-based design for seismic retrofit of existing buildings using nonlinear viscous dampers［J］.Journal of Structural Engineering，2008，134(4):671-681.

［10］吴从晓，周云，邓雪松，等.高位转换粘滞阻尼减震结构阻尼器合理阻尼系数研究［J］.振动与冲击，2011，30(3):180-184.

［11］郭彦林，刘建彬.结构的耗能减震与防屈曲支撑［J］.建筑结构，2005，35(8):18-23.

［12］刘建彬.防屈曲支撑及防屈曲支撑钢框架设计理论研究［D］.北京:清华大学土木工程学院，2005.

［13］CHOIH K M.Energy-based seismic design of buckling-restrained braced frames using hysteretic energy spectrum［J］.Engineering Structures，2006，28:304-311.

［14］李霆，王小南.武汉保利广场混合减震连体高层结构设计［J］.建筑结构，2012，42(12):1-7.

［15］李霆，王小南.武汉保利广场混合减震连体高层抗震性能研究［J］.建筑结构，2012，42(12):8-12.

［16］沈聚敏.抗震工程学［M］.北京:中国建筑工业出版社，2000.