基于APOS理论的高中数学概念教学——以“直线的倾斜角与斜率”的概念教学为例

角碧波 张湘君

（云南省昆明市第八中学，昆明650222 湖南师范大学附属中学，长沙 410006）

一、问题的提出

概念教学在高中数学教学中举足重轻.传统的概念教学中典型的做法是：教师带领学生勾画概念，强调若干注意点，随即开始大量做题，试图通过让学生不断地解题来促进学生对概念的理解.而这种做法的结果往往适得其反，学生变成了解题机器，只知其然而不知其所以然.寻求新的有效的概念教学法是高中数学教与学的迫切需要，也是广大高中数学教师的不懈追求.APOS理论是美国学者杜宾斯基（Dubinsky）等人提出的一种建构主义的数学学习理论［1］，它的主张概念建构要具有层次性的观点为数学概念教学的逐层渐进提供了理论基础.本文试图基于APOS理论，以平面解析几何的开篇和基础——“直线的倾斜角与斜率”为例，尝试对高中数学概念教学进行探索，以期获得一些启发.

二、APOS理论

APOS由“Action（操作）”“Process（过程）”“Object（对象）”和“Schema（图式）”四个英文单词的首字母组合而成［1］，杜宾斯基认为数学概念的学习要经历这四个活动阶段.APOS 理论是源于杜宾斯基试图对皮亚杰（Piaget）数学学习的“自反抽象（Reflective Abstraction）”理论进行拓展的一种尝试［2］.

1.“操作（A）阶段”——学生建构数学概念的起点

教师基于学生已有认知的基础，为学生提供概念的直观背景、相关概念或是一些感性素材，学生对这些外部刺激进行感知和转换.在数学概念中学生的“操作（A）”是广义上的活动，可以是具体的动作操作，也可以是抽象的思维操作［3］.

2.“过程（P）阶段”——学生概念学习的关键阶段

在“操作（A）阶段”学生获得了直观感知，在随后的这一阶段，就要对其进行组织和处理，经历观察、联想、归纳和概括等过程，才有思考和顿悟，实现知识的内化和压缩.在这一阶段需要充分暴露思维的过程，才能实现知识的“再创造”，其短暂或缺失，都会影响学生的参与度和学习效果，并直接影响“对象（O）阶段”概念的概括和生成.

3.“对象（O）阶段”——学生概念学习的概括阶段

“操作（A）”和“过程（P）”两个阶段的达成度将直接影响此阶段的时间、效率和质量.经历一次或数次“操作（A）”和“过程（P）”后，学生在大脑中对活动不断进行描述和反思，抽象概括出概念所特有的性质，从而在头脑中生成对概念的认知和初步把握.

4.“图式（S）阶段”——学生习得概念的升华阶段

教师提供反映概念的特例、抽象过程、定义和符号等情境给学生探究，学生对其进行深入学习.对前面几个阶段的经历及大脑中原有相关方面的问题图式进行不断的整合、精致，最终实现数学概念的建构，形成综合的心理图式.概念一旦建构起来，就将成为后续的概念建构的材料.

值得指出的是，有的数学概念的学习，一两次的“APOS”是不能形成完整的“图式（S）”的［3］，如函数概念的学习是一个复杂而困难的过程［4］，学生在初中、高中和大学都需要经历不同程度的概念建构.

三、基于APOS理论的“直线的倾斜角与斜率”的概念教学活动设计

“直线的倾斜角与斜率”是普通高中课程标准实验教科书数学人教A 版必修2 第三章第一节的第一小节内容［5］，本小节内容涉及两个核心概念的教学——辅概念“倾斜角”和主概念“斜率”1在数学学习中常常会遇到这样的情况：在学习一个知识点之前需进行一些必要的预备知识的学习.我们称最终要学习的概念为“主概念”，为此需要进行预备学习的概念为“辅概念”.，现基于APOS理论对两个概念的教学活动过程进行设计2本文主要处理“倾斜角”和“斜率”两个核心概念的教学设计，其他教学内容和环节在此不予涉及..

1.直线的倾斜角

（1）操作（A）阶段

问题1：在初中我们已经学习过一次函数，知道其图象是直线，图1是在同一直角坐标系中给出了某三个一次函数的图象，它们有什么区别与联系？

师生活动：（1）引导学生发现三条直线图象的联系是过同一个点（1，0），区别是倾斜程度不同；（2）用几何画板演示过定点（1，0）的直线系（如图2），帮助学生思考“区别”；（3）得出结论：两点确定一条直线，过一点不能确定一条直线.

图1

图2

【设计意图】“一次函数及其图象”和“两点确定一条直线”是初中就已学过的内容，以此作为“生长点”，基于已有认知而又高于已有认知，形成认知冲突，启发学生思考，激发学生学习兴趣.

（2）过程（P）阶段

问题2：上述问题中我们所谓的直线的倾斜程度应该是相对的，分别以x轴、y轴为参照，同一条直线的倾斜程度是不一样的，我们不妨以x轴为参照进行研究.在直角坐标系中，任何一条直线与x轴都有一个相对倾斜程度.请同学们思考可以用什么样的一个几何量来反映一条直线与x轴的相对倾斜程度.

师生活动：引导学生把重点放在“如何描述直线倾斜程度”的问题上，启发学生发现可以用直线与x轴形成的夹角（当直线与x轴相交时）来描述直线的倾斜程度.当然，直线与x轴相交会形成四个角，教师还需引导学生思考到底选哪个角作为刻画直线倾斜程度的几何量比较合适.在这一系列引导学生的思考中促成概念的形成.

【设计意图】充分暴露思维的过程，引导学生做数学，自然而然探索得到描述直线倾斜程度的几何要素，此即概念生成的过程.

（3）对象（O）阶段

问题3：我们探究得到的描述直线倾斜程度的角简称直线的倾斜角，请同学们用自己的语言尝试着给倾斜角下一个定义.

师生活动：鼓励学生大胆发言，交流意见，引导学生在碰撞中归纳总结出直线倾斜角的概念.

【设计意图】想清楚了还需说清楚，说清楚了才能写清楚，基于前面问题2的充分探究，可以把舞台让给学生，锻炼学生的数学言语表达和归纳能力.

（4）图式（S）阶段

练习1 判断正误：（1）存在倾斜角是210°的直线；（2）存在倾斜角是180°的直线；（3）直线确定，则倾斜角确定；（4）倾斜角确定，则直线确定.

师生活动：先给学生时间做，必要时进行适当引导，而后再借助几何画板进行讲评.

【设计意图】（1）（2）帮助学生再次理解直线倾斜角的含义，并得出直线倾斜角取值范围的规定；（3）（4）旨在引导学生理解直线与倾斜角的对应关系，明确确定一条直线位置的几何要素.

2.直线的斜率

（1）操作（A）阶段

问题4：我们在生活中，骑车或步行都爬过山、爬过坡，陡的坡感觉比较难爬，如何描述坡的陡缓程度呢？（几何画板演示：将实际生活中的斜坡抽象成如图3所示，动态演示升高量、前进量改变时坡的陡缓程度的变化.）

师生活动：教师引导与演示，启发学生积极思考（可提示学生用书本模拟），再现初中就已经接触过的“坡度”概念（坡度＝升高量／前进量＝tanα）.

图3

【设计意图】基于学生客观认知水平，结合已有生活经验寻找几何要素代数化的方法.引导学生发现，坡的陡缓程度与前进量和升高量有关，帮助学生再现“坡度”概念.

（2）过程（P）阶段

问题5：在图3中，∠BAC是斜坡构成的二面角的平面角.在平面ABC中，将斜坡对应直线AC，坡角对应直线AC的倾斜角α，那么坡度对应直线AC的什么量呢？

师生活动：引导学生把“坡度”这个刻画倾斜程度的量与直线倾斜角联系起来，进行类比，从而发现tanα可以作为直线倾斜程度的一个代数表示.

【设计意图】通过类比，探索描述直线的倾斜程度的代数表示，由此引出直线斜率的概念.

（3）对象（O）阶段

问题6：请同学们类比倾斜角概念的给出，给直线倾斜程度的代数表示起个名字，并下一个定义.（注：师生活动与设计意图同问题3.）

（4）图式（S）阶段

练习2 填表

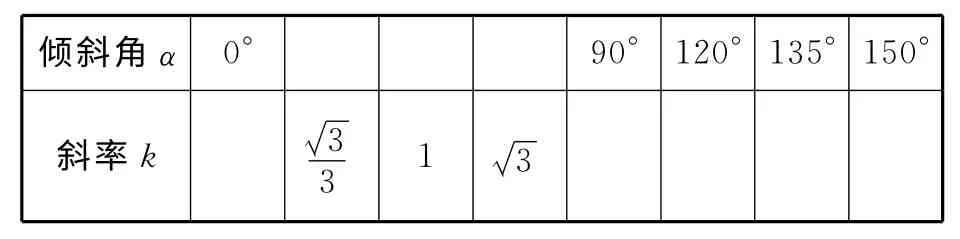
师生活动：先让学生独立去做，而后与学生一起订正.（正切是学生在三角函数中理解的一个难点，需留给学生充分的时间去回顾必修4里的正切相关知识.）

【设计意图】使学生学会倾斜角与斜率的互换，学会求倾斜角是钝角时的直线斜率，明确“倾斜角为90°的直线斜率不存在”，深化斜率概念的理解，与此同时为后续问题7做铺垫.

问题7：请同学们借助正切函数的图象，思考倾斜角α与斜率k有何关系？

师生活动：如图4，引导学生回忆y＝tanx的图象，结合y＝tanx在区间上的图象总结出斜率与倾斜角之间的关系.

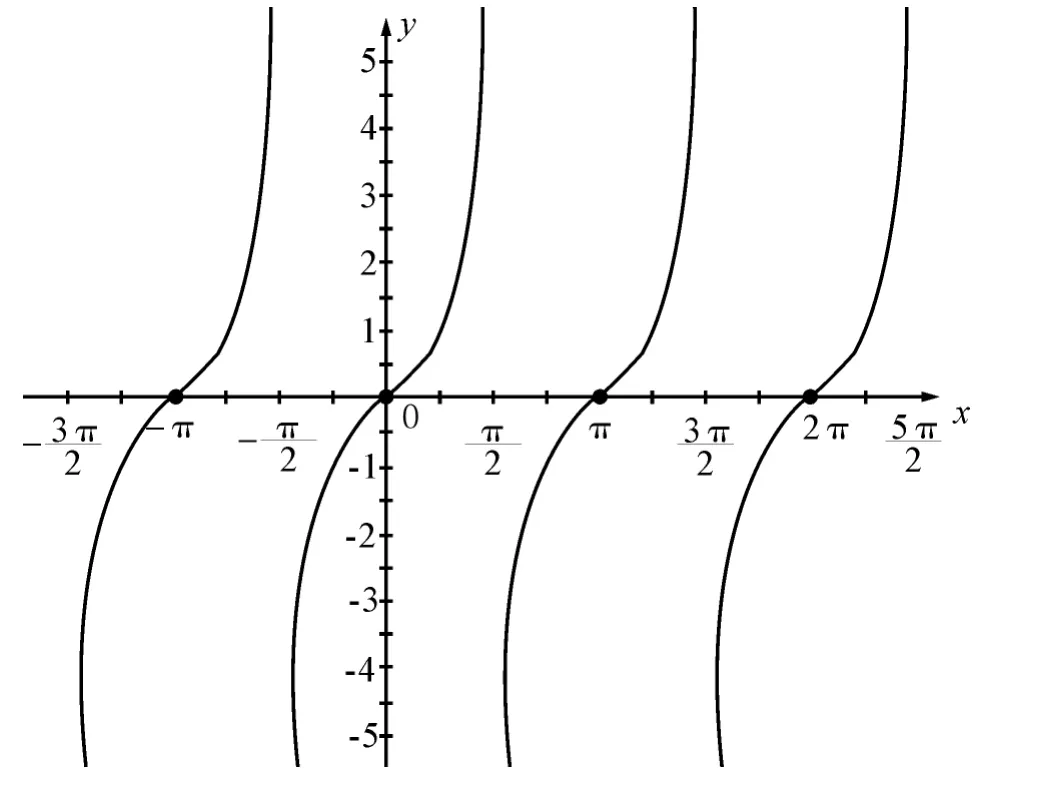
图4

【设计意图】沟通数形关系，加深概念理解，让学生明确倾斜角与斜率的关系，体会倾斜角与斜率的内在联系.

练习3（1）判断正误：①与x轴平行或重合的直线没有斜率；②直线的倾斜角为α，则它的斜率为tanα；③直线斜率为tanα，则它的倾斜角为α；④直线的倾斜角越大，则它的斜率也越大.

（2）如图5 所示，直线l1，l2，l3的斜率分别为k1，k2，k3，试比较它们斜率的大小.

图5

师生活动：让学生先自己做，再小组讨论，组织小组间博弈，教师充当组织者、引导者的角色.

【设计意图】（1）是针对斜率概念的理解而设计；（2）是综合倾斜角和斜率两个概念的理解与应用而设计.

四、基于APOS理论的高中数学概念教学

在实际教学中我们发现，学生在数学概念的建构过程中，大多数都能达到“操作（A）阶段”和“过程（P）阶段”，到“对象（O）阶段”的学生就少了许多，能达到“图式（S）阶段”的则更少一些.我们知道，“对象（O）阶段”的达成取决于“操作（A）阶段”“过程（P）阶段”的充分铺垫，有文献［6］总结了对“操作（A）阶段”“过程（P）阶段”的教学建议：（1）用新奇的操作，燃起思考的火花；（2）以递进的问题导引思维的纵深.因此，“操作（A）阶段”中的引导和“过程（P）阶段”中对数学思维过程的暴露尤为重要，需要教师在教学设计时精心设计情境引入和问题串，在教学过程中留给学生足够的思考和探究的时间，避免“短、平、快”的现象发生.

学生对知识真正意义的理解与建构是建立在亲历操作的基础上的，APOS理论为概念教学提供了一个操作层面的指导［6］，让学生在“操作（A）阶段”中体验、在“过程（P）阶段”中感悟、在“对象（O）阶段”中归纳、在“图式（S）阶段”中升华.在高中数学教学中进行以APOS理论为指导的概念教学设计，可以大大改善高中数学概念教学.

［1］Dubinsky E.APOS：A Constructivist Theory of Learning in Undergraduate Mathematics Education Research［C］.1993.

［2］乔连全.APOS：一种建构主义的数学学习理论［J］.全球教育展望，2001（03）：16－18.

［3］程华.APOS理论的内涵及其对中学数学概念教学的启示［J］.教学与管理，2010（24）：65－66.

［4］孟世才.基于APOS理论的中学函数概念的教学研究［J］.教学与管理，2011（21）：95－96.

［5］课程教材研究所.普通高中课程标准实验教科书·数学必修2（A 版）［M］.北京：人民教育出版社，2004.

［6］程华.在操作中体验，从过程中感悟，在感悟中建构——对APOS理论操作、过程阶段的思考［J］.数学教学研究，2007（5）：2－5.