数理统计在原油计量和检验工作中的应用

马应奎

中国检验认证集团新疆有限公司(新疆乌鲁木齐830011)

数理统计在原油计量和检验工作中的应用

马应奎

中国检验认证集团新疆有限公司(新疆乌鲁木齐830011)

以中哈原油管道计量和检验工作为例，通过几个不同的案例介绍了置信区间、t检验和方差分析等数理统计工具在原油的密度检测、水分检测、动态计量流量计系数修正、不同检测标准间检测结果比对以及检测影响因素分析等工作中的应用。通过数理统计工具严谨的推论，可以有效地解决一些实际工作中结论论据不充分、论证过程不够严谨的问题，使计量检验工作中常见的数据对比分析工作论证更加充分，结论更加科学严谨。

原油检验;数理统计;商品检验;置信区间;t检验;方差分析

计量和检验是质量管理的重要内容之一，属于技术服务领域。要想在激烈的市场竞争中占有一席之地，获得好的收益，就要不断的提高服务的技术含量。高技术含量的业务往往也是高收益的业务，竞争对手少，利润率高，处于行业的高端。数理统计是质量管理非常重要的工具之一，作为从事计量和检验服务的质量控制从业人员，应该很好地掌握并将其应用在工作中。

1 应用案例

1.1 置信区间的应用案例

我国第一条跨国原油管道——中哈原油管道计量检验业务中，业主单位要求的其中一项工作是对每一批次原油(24h为一批次)实验室离线检测的密度值和安装在管线上在线密度仪检测值进行对比，每10个批次的对比结果向业主单位提交一次对比分析报告。当两检测值差异出现偏离时应立即向业主单位通报并检查检测过程是否出现失控。实验室离线检测的样品为自动取样系统或人工取样的24h混合样，检测方法为密度计法［1］;在线密度仪的检测值为24h检测值的加权平均值，检测方法为U型管振荡法［2］。可以近似认为这种对比是对同一样本的不同检测方法的对比。如何判断两检测值间的差异是否出现偏离呢?可以用再现性进行判断。相关检测标准中:对于原油，按实验方法正确操作得到的2个独立结果之间的差，在长期操作实践中，超过1.5kg/m3的概率只有5%。

现随机抽取2个对比时间段(10d)的在线和离线密度数据，差值情况见表1。

表1中所列两对比组的在线密度与离线密度之间的差异是否偏离了正常值呢?在长期操作实践中，差值超过1.5的概率只有5%。有人认为2个对比组中均有20%的差值数据超过了1.5，(第一组中为-1.6和-1.7，第二组中为-1.6和-1.8)大于标准给定的5%的概率，所以根据2个对比组的对比结果，应判定检测过程出现异常。这样的判断方法显然是不对的。

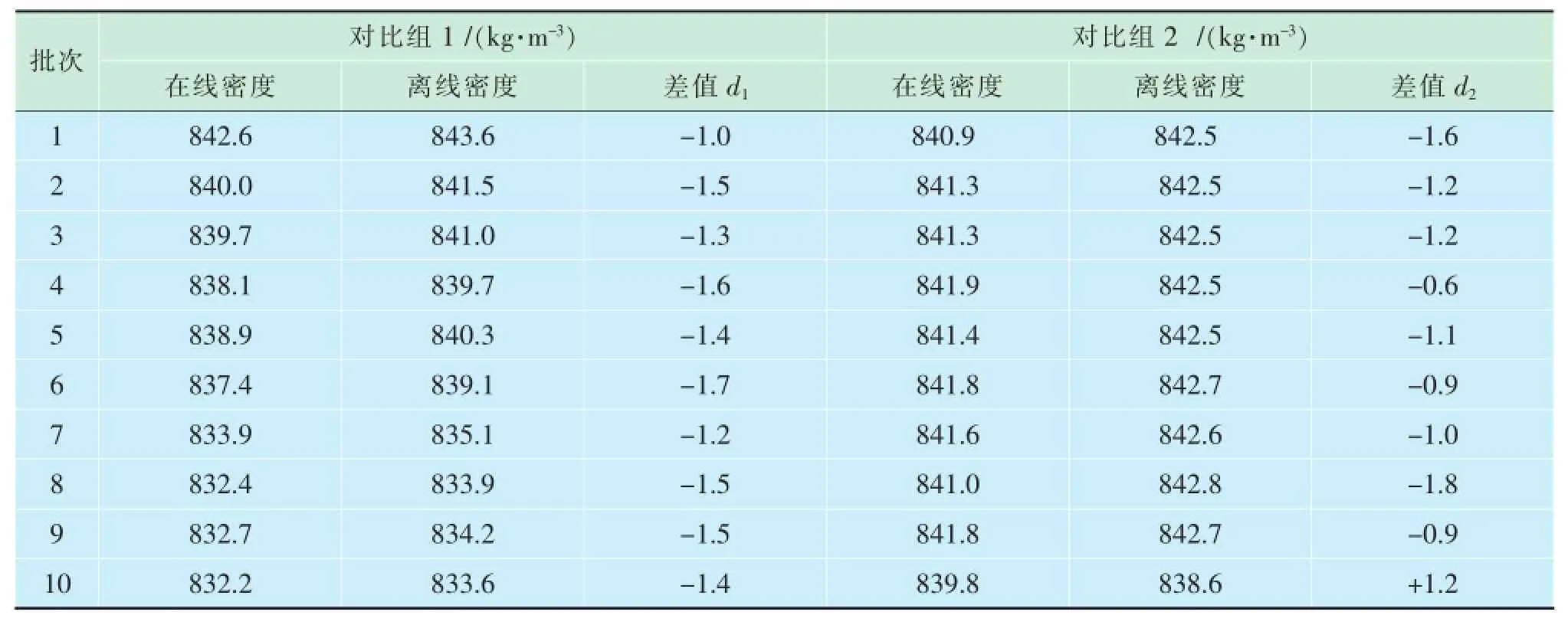
表1 随机抽取的两组在线密度与离线密度差异

这是一个用样本估计总体的区间估计问题。标准中“在长期操作实践中，差值超过1.5的概率只有5%。”在95%的置信区间下，两检测结果的差值的不超过1.5，即95%的置信区间为［-1.5，1.5］。要判断一个对比组的差值是否出现偏离，应计算出其95%的置信区间是否在［-1.5，1.5］内。下面计算表1中2个对比组的95%置信区间。

首先计算两对比组差值的均值和标准差:

样本量n1=n2=10，所以自由度df1=df2=n1-1=n2-1=10-1=9。

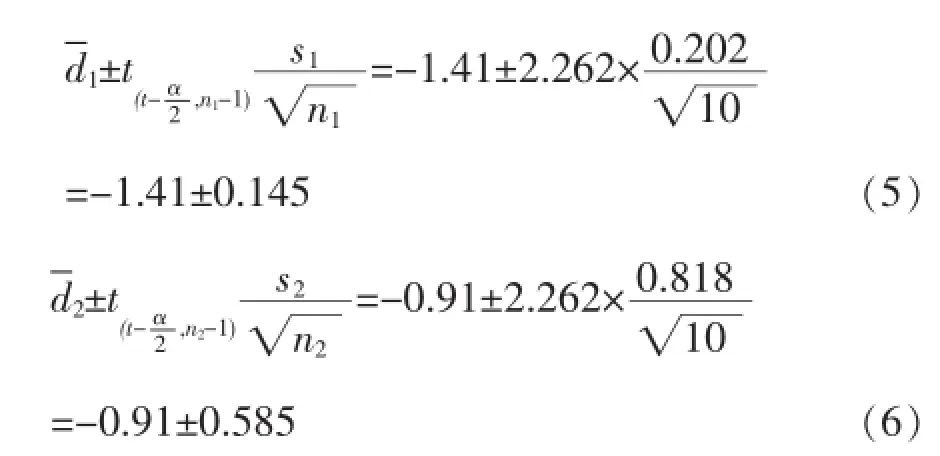
从以上计算可得出，对比组1的95%置信区间为［-1.555，-1.265］，已超过了标准给定的［-1.5，1.5］差值区间，应判定差值出现偏离，对两种检测方法的各过程进行检查，消除原因。对比组2的95%置信区间为［-1.495，-0.325］，在标准给定的［-1.5，1.5］差值区间内，应判定差值未出现异常。

因为样本量n=10和置信水平95%是固定的，标准给出的置信区间［-1.5，1.5］也是固定的，因此，两方法检测差值的置信区间可转化为不等式的求解问题:

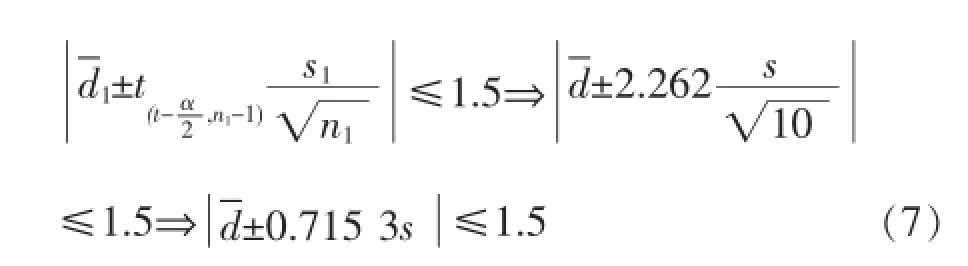
1.2 t检验应用案例

1.2.1 单样本的t检验

中哈原油管道阿拉山口计量站是中哈两国认可的交接计量点，使用双转子流量计进行动态连续计量。双方约定每6个月由中哈两国计量院对流量计进行一次共同检定。为监控流量计的计量准确性，每个月由业主单位中哈管道公司(KCP)、政府监管单位CIQ、计量服务提供商CCIC、运营单位西部管道共同对流量计进行一次在线实流校验，并根据校验结果对流量计进行系数修正。由于流量计为0.2级，即最大允许误差不超过0.2%［3］。当校验所得流量计脉冲系数K与经检定录入系统的在用脉冲系数K0差值不超过0.2%时，不必对流量计进行系数校正。某台在用流量计检定脉冲系数K0为10 235.822，对其进行在线校验，所得数据见表2。

是否应根据此次校验结果对该流量计的K系数进行调整呢?如果按照基本误差法有:

(10 228.968 6-10 235.822)/10 235.822=-0.067%

显然0.067%远小于0.2%，可以不对该流量计进行系数修正。

表2 在线实流校验结果

如果用数理统计的方法对此次校验结果进行分析，这就是一个单样本的t检验问题(双侧检验)。表2中已经计算出均值μ=10 228.968 6，取检验水平α=0.05，则有

查t临界值表，t(0.05，4)=2.776，3.328＞2.776，此次在线实流校验所得脉冲系数K与在用脉冲系数K0存在显著差异。应对该流量计进行系数修正:该流量计每月计量原油50×104t，如不进行流量计系数修正，则少计量原油达到335t，货值达170多万元。

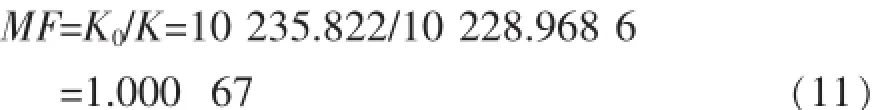
1.2.2 独立样本的t检验

在管输原油流量计动态计量方面，独联体国家与我国的计量体系没有明显的差别，计量交接结算也均以净重为准。但我国原油净重的计算是毛重扣除水分和机械杂质后的重量［4］，而独联体国家原油净重的计算在扣除水分和机械杂质外，还要扣除盐含量［5］。由于两国在水分、机械杂质和盐含量(以上3项的总和一般称为原油的总杂)的检测方法和检测周期上均存在一定差别，中国阿拉山口末站累计检测原油总杂绝对数量最高时比哈萨克斯坦阿塔苏首站高出2万余吨，总货值高达上亿元人民币，导致双方对彼此检测结果相互质疑等一系列问题。

为了弄清两站间原油总杂数量相差较大的原因，对中哈原油管道哈萨克斯坦阿塔苏首站及中国阿拉山口末站两站连续15个月的品质检测结果进行了统计分析。分析发现，两站的机械杂质的检测结果基本相同，盐含量检测结果虽然存在较大差异，但检测值都比较低，仅为10-5数量级，其对原油总杂的影响可以忽略不计。最终得出两站间原油总杂差异较大的主要原因应该是水分含量检测结果的差异。

由于阿塔苏站水分检测采用的是ΓOCT 2477［6］标准，阿拉山口站采用的是ASTM D 4006［7］标准。为了研究两种不同的检测方法的检测结果是否存在明显差异，将随机抽取的某日样品分别按照ASTM D 4006与ΓOCT 2477标准进行平行检测，结果见表3。

由表3已知:n1=5，s1=0，=0.200;n=10，s2= 0.023 6，=0.017 4。两种检测方法的检测结果是否存在着显著性差异，是一个独立样本的t检验问题，可以使用假设检验进行判断。

查t临界值表t(0.05，9)=1.833，

有3.474＞1.833，所以，拒绝原假设H0，接受备择假设Ha。即在0.05显著性水平下，ΓOCT 2477的检测结果均值小于ASTM D 4006的检测结果均值。通过假设检验对对比实验结论的充分论证，该结论获得了中哈双方专家的认可，很好的解决了两国间水分检测值差异较大的原因分析问题。

1.3 方差分析应用案例

在原油检验过程中，原油的密度是一项非常重要的检测项目。在使用密度计法检测原油密度时，除了密度计本身的精度外，检验人员的操作水平是影响检测结果主要因素。为了比较3名不同的检验员操作水平是否会对检测结果产生直接影响，组织了一次检测试验。对同一样品由3名检验员使用同一密度计分别做5次平行检测，结果见表4。

要想知道不同检验员的检测结果间是否存在显著性差异，可以进行方差分析。方差分析计算过程比较繁琐，手工计算数据量大，现已普遍使用计算机软件进行计算。以下是使用IBM SPSS Statistics 20软件计算的结果(显著性水平为0.05)(表5、表6)。

方差分析的显著性水平0.011＜0.05，组间存在显著性差异，所以参加试验的3名检验员间存在由操作导致的检测结果显著性差异。具体是哪一名检验员与其他两名检验员间存在显著性差异还是3名检验员间均存在显著性差异，需要进一步进行多重比较。已知方差齐性，选择较为灵敏的LSD法(最小显著差法)，SPSS计算的多重比较检验结果见表7。

表3 ASTM D 4006和ΓOCT 2477水分含量检测结果/%

表4 3名检验员原油密度的检测结果/(kg·m-3)

表5 方差齐性检验

表6 单因素方差分析

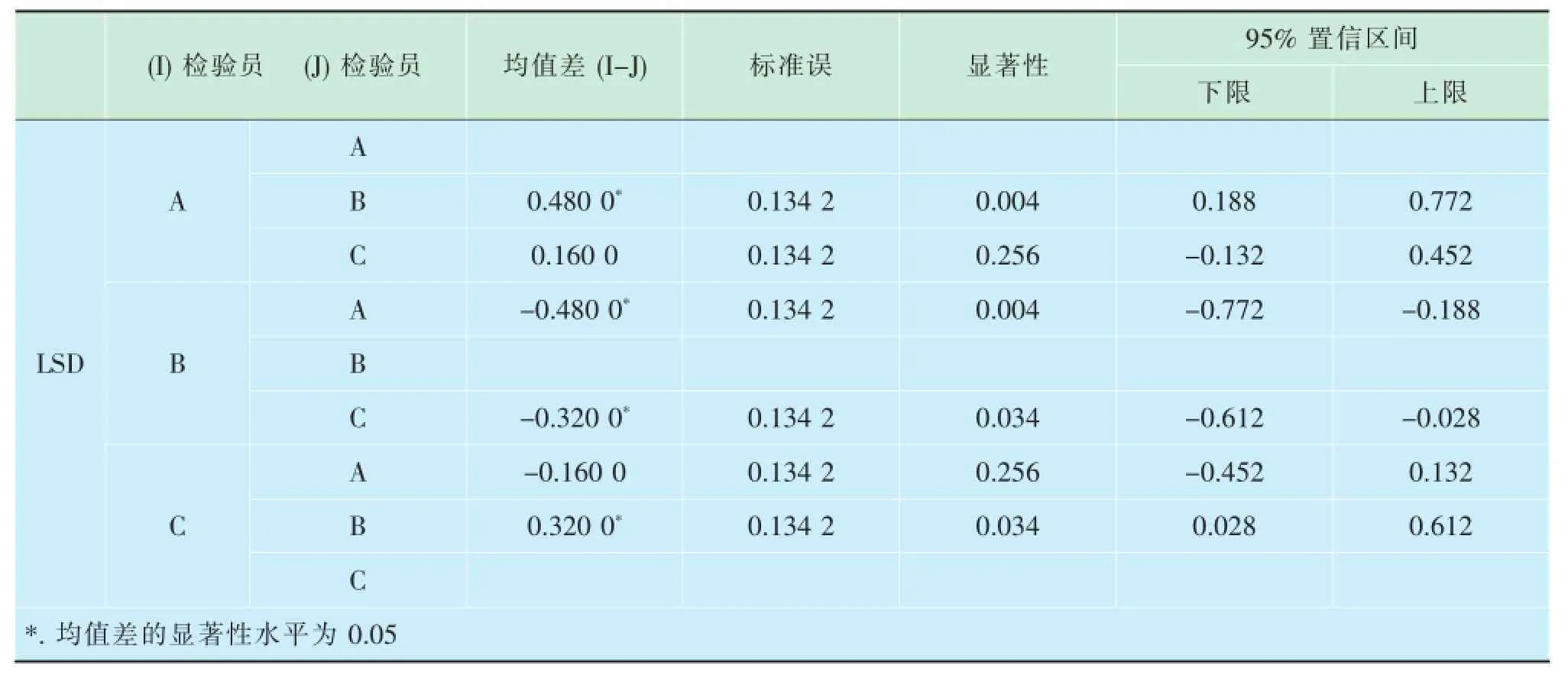
表7 多重比较检验结果

由多重比较检验结果可知，检验员A和检验员C的检测结果间不存在显著性差异，检验员B和检验员A、C的检测结果间均存在显著性差异。因此检验员B的操作过程可能存在不规范处，应对其操作过程进行详细检查，以尽量降低人为因素对检测结果造成的影响。

2 结论

通过数理统计工具的应用，可以很好地解决工作中遇到的许多实际问题，如无明确判定标准、差异原因分析等。可以提升各类报告的专业化水平，使论证过程更加严谨，结论依据更加充分，树立专业化质量管理的良好形象。

［1］GB/T 1884-2000原油和液体石油产品密度实验室测定法(密度计法)［S］.

［2］SH/T 0604-2000原油和石油产品密度测定法(U形振动管法)［S］.

［3］JJG 667-2010液体容积式流量计检定规程［S］.

［4］GB/T 9109.5-2009石油和液体石油产品油量计算动态计量［S］.

［5］ΓOCT P 8.595-2004石油与石油产品的质量对测定方法的总要求［S］.

［6］ASTM D 4006-2011原油水含量的测定蒸馏法［S］.

［7］ΓOCT 2477-65(82)石油产品水分测定法［S］.

Taking themeasurement and inspection of China—Kazakhstan pipeline crude oil as an example，the application of confidence interval，t-test and variance analysis in crude oil density inspection，water content inspection，flowmeter coefficient correction，the inspection result comparison of different inspection standards and the influencing factor analysis of inspection results.The rigorous reasoning ofmathematical statistics tools solves the problems thatevidence is not sufficientand argument is not rigorous，whichmakes the argument of the data analysis in themeasurement and inspection of crude oilmore sufficient and the conclusions aremore rigorous and scientific.

crude oil inspection;mathematical statistics;commodity inspection;confidence interval;t-test;variance analysis

左学敏

2014-08-07

马应奎(1976-)，男，工程师，主要从事石油及天然气计量和检测相关工作。