IFS-LSSVM及其在时延序列预测中的应用

田中大，李树江，王艳红，高宪文（.沈阳工业大学信息科学与工程学院，辽宁沈阳 0870；.东北大学信息科学与工程学院，辽宁沈阳 089）

IFS-LSSVM及其在时延序列预测中的应用

田中大1，李树江1，王艳红1，高宪文2
（1.沈阳工业大学信息科学与工程学院，辽宁沈阳 110870；2.东北大学信息科学与工程学院，辽宁沈阳 110819）

∶针对最小二乘支持向量机预测模型中最优参数难以确定的问题，提出一种基于改进的自由搜索算法确定最小二乘支持向量机最优参数的方法（IFS-LSSVM）。对标准自由搜索算法进行改进，使之可应用于最小二乘支持向量机的参数优化，改进之后的算法具有更好的优化性能。将具有时间序列性质的网络时延作为预测对象，利用本文的IFS-LSVM算法进行预测。在仿真中与遗传算法优化的最小二乘支持向量机（GA-LSSVM）、粒子群优化算法优化的最小二乘支持向量机（PSOLSSVM）、标准最小二乘支持向量机工具箱中的网格搜索算法（Grid-LSSVM）进行了对比。仿真对比结果表明本文的方法具有更高的预测精度与更小的预测误差。

∶最小二乘支持向量机；自由搜索；时延序列；预测；时间序列

0 引言

支持向量机（supportvectormachines，SVM）在模式识别、时间序列预测、非线性建模等领域有着广泛应用［1］。为简化SVM的计算复杂性，缩短计算时间，Suykens等人在1999年提出了最小二乘支持向量机（leastsquaressupportvectormachines，LSSVM）［2］，LSSVM采用最小二乘线性系统作为损失函数，用等式约束代替不等式约束，从而避免了计算复杂的二次规划问题。

网络中的时延具有时变和随机的特性［3-4］，具有强烈的非线性，因此可将网络时延作为预测对象来考察非线性预测模型的精确性，目前对于网络时延序列的预测方法中，文献［5-7］认为在某一观测尺度内，时延集合可视为平稳的时间序列，因此对时延可通过自回归（autoregressive，AR）为基础的方法建模与预测，但是采用自回归预测方法需要对模型精确建模，其模型的参数求解过程复杂，很难在线递推，不适合网络时延动态变化范围很大的情况。神经网络具有非线性辨识能力，且运算速度快，因此可使用神经网络来进行时延序列的预测［8-10］，但基于神经网络的时延预测方法存在的问题是易限于局部最优值以及过分依赖输人时延序列的自相关系数。而SVM和LSSVM在非线性、小样本以及高维模式识别问题中有独特的优势，非常适合具有强烈非线性特点的网络时延的预测［11-12］，但是基于SVM或LSSVM的算法的参数选取没有确定的理论依据，算法参数对于预测结果精度的影响很大。

本文为了确定LSSVM预测模型中的最佳参数，利用自由搜索（freesearch，FS）算法良好的全局优化特点，对标准自由搜索算法进行改进，建立改进自由搜索算法的最小二乘支持向量机（improvedfree searchleastsquaressupportmachines，IFS-LSSVM）预测模型，并将网络时延作为预测对象，与遗传算法优化的LSSVM（geneticalgorithmLSSVM，GA-LSSVM）、粒子群算法优化的LSSVM（particleswarmoptimization，PSO-LSSVM）、网格搜索法寻优的LSSVM（Grid-LSSVM）进行了对比，并通过仿真验证了本文方法的有效性。

1 时延预测的LSSVM模型

定义如下的时延样本矢量

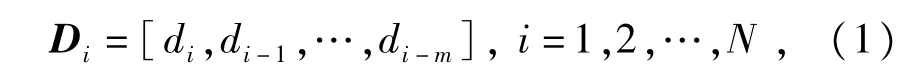
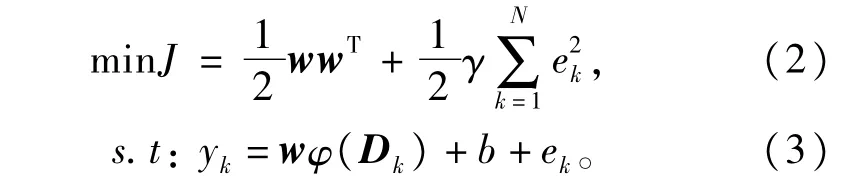
式中∶J代表二次优化问题的目标函数，w为权系数向量，φ（.）为非线性映射，其将输人向量映射到高维的希尔伯特空间，γ为正则化参数，b为常值偏差，ek为训练误差，建立拉格朗日函数求解上述的约束优化问题∶

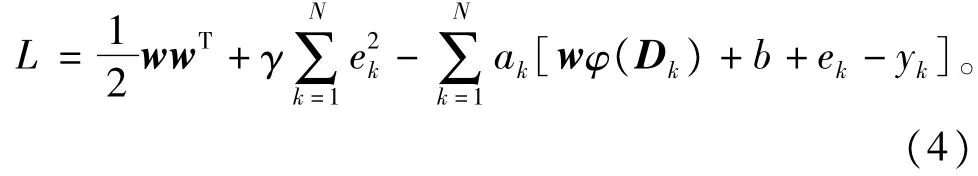
根据Karush-Kuhn-Tucker（KKT）最优条件［13］，可得到∶

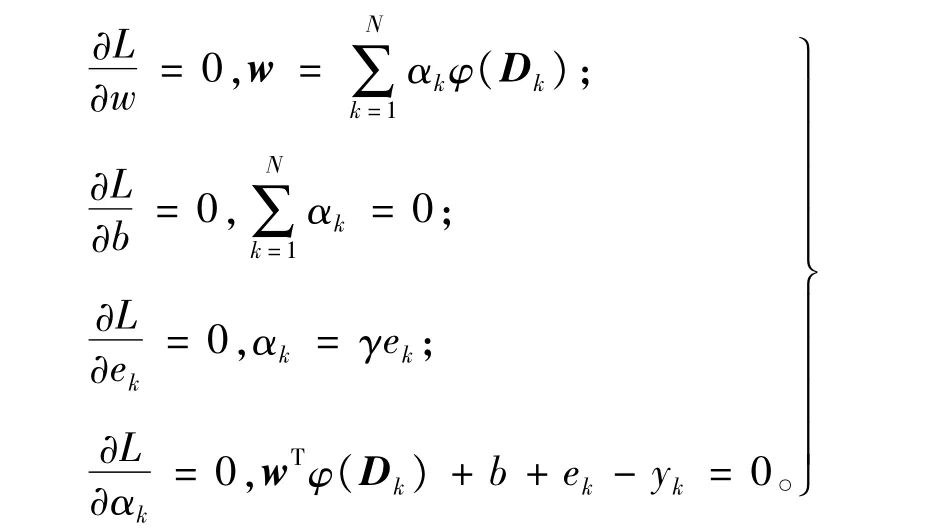
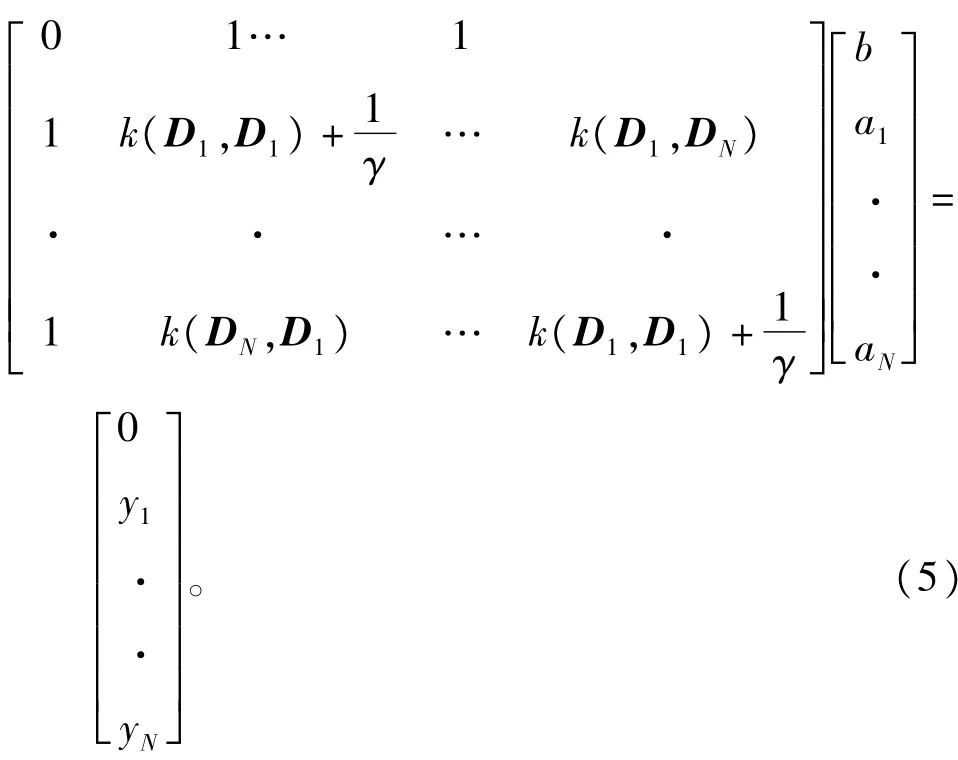
消元去掉w和ek则得到∶

式中k（.）为核函数，在回归预测中一般选择式（6）所示的径向基函数（radialbasisfunction，RBF）作为核函数［14］

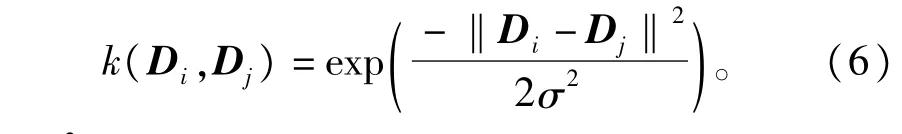
式中σ2为径向基的核函数宽度。由以上各式可得k+1时刻的网络时延预测值为∶

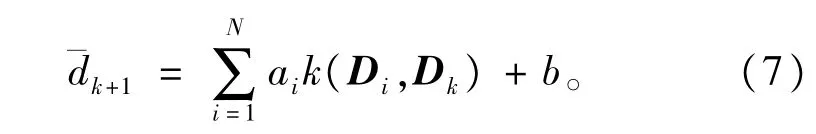
设输人的时延序列为D，将D转化为下式（8）所示的矩阵形式∶

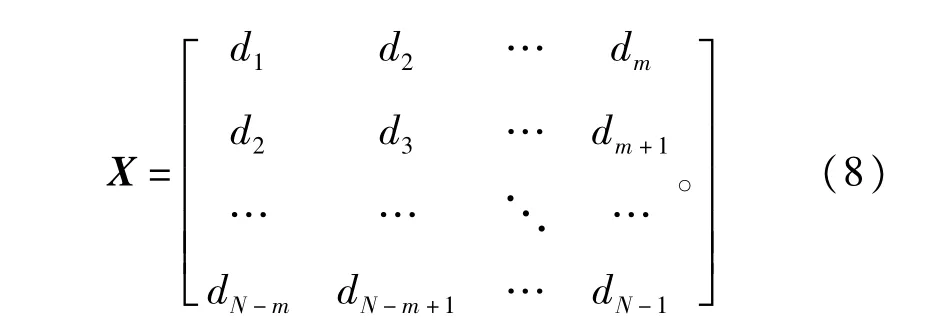
其中∶dt代表t时刻的时延值；N为输人时延序列的总长度；m为嵌人维数；矩阵X是维数为（N-m）× m的矩阵，而输出的预测时延可表示为式（9）的（N -m）×1维矩阵Y∶

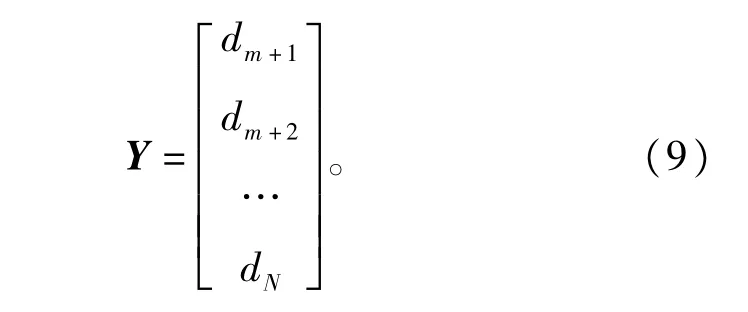
由式（8）与式（9）可知，X与Y的关系相当于用当前时刻时延与过去m个时刻的时延来预测未来时刻的时延。基于LSSVM的时延预测方法可表示为如下步骤∶

步骤1∶取N组样本时延数据，选择合适的预测参数γ，σ2，m；

步骤2∶将样本数据按照式（8）与式（9）转换为输人与输出向量；

步骤5∶将预测值作为实际值代人时延序列，重复运行，预测未来多个时刻的时延，直到结束。

从以上的描述可知，利用LSSVM算法对时延预测的关键参数为正则化参数γ，径向基的核函数宽度σ2，然而γ和σ2对于LSSVM性能的影响在理论上没有确定的依据，对于如何选取合适的γ和σ2没有确定的方法［15］。同时本文测试发现时延序列的嵌人维数m对于预测的精度也存在一定的影响，合理的选择γ、σ2、m这3个参数将极大的影响预测的精度。为了定量说明3个参数对于预测精度的影响，图1为γ∈［0.1，1］，σ2∈［0.1，1］，m=5，图2 为m∈［1，10］，γ=1，σ2=1时100组预测时延与实际时延误差的均方误差（meansquareserrors，MSE）的变化曲线，从图1与图2中可看出3个参数不同的取值其预测精度是不同的。

为了确定预测模型中的最优参数，本文下节提出一种改进的自由搜索算法来完成参数的优化选取。

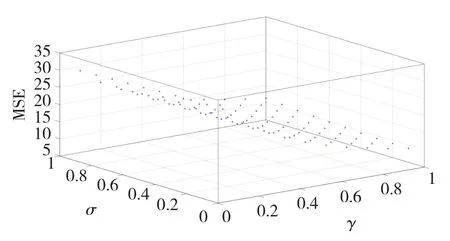
图1 γ与σ2不同取值时的MSE分布Fig.1 MSEdistributionwhenγandσ2with differentvalues

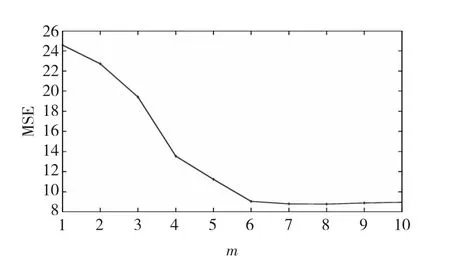
图2 m不同取值时的MSE分布Fig.2 MSEdistributionwhenmwithdifferentvalues

2 改进的自由搜索算法

2.1 标准自由搜索算法

自由搜索算法是2005年提出的一种新的基于群体的优化方法［16］，其算法包括初始化、寻优搜索与终止判断。其算法描述如下∶m代表个体的数量，j，（1≤j≤m）为第j个个体，k，（1≤k≤m）为信息素标记坐标点，n为目标函数的变量数也就是搜索空间的维数，i（1≤i≤n）代表变量的第i维，T为搜索步中的小步数，t（1≤t≤T）是搜索步中的当前小步，Rji（Rji∈［Rmin，Rmax］）是第j个个体在搜索空间第i维变量空间邻域搜索范围，G是搜索终止代数。自由搜索算法种群的初始化一般采用如下的策略∶

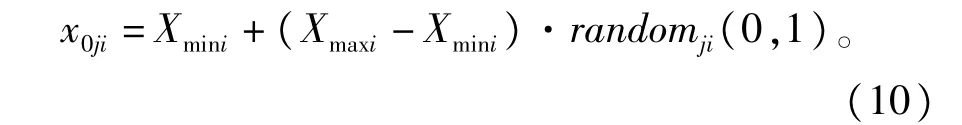
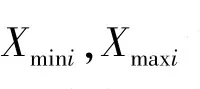
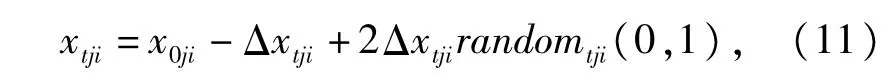
其中∶xtji更新后的动物个体位置分量，在自由搜索算法模型中，个体移动一个搜索步，每个搜索步包含T小步，个体在多维空间作小步移动，其目的是发现目标函数更好的解。其修改策略Δxtji为∶

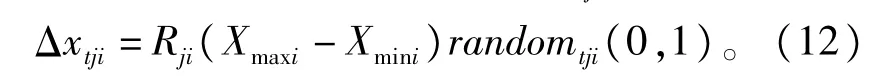
个体搜索过程中对目标函数符号作如何规定∶

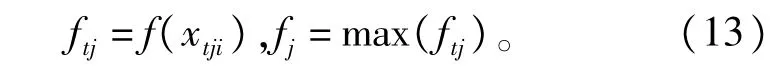
定义如下更新的信息素∶

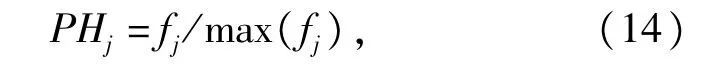
定义灵敏度SEj按如下更新∶

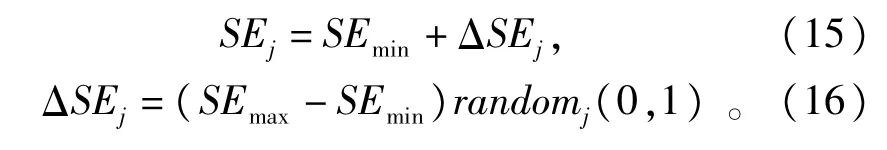
其中SEmin=PHmin，SEmax=PHmax。

在一轮搜索结束后，确定下一轮搜索的起始点。

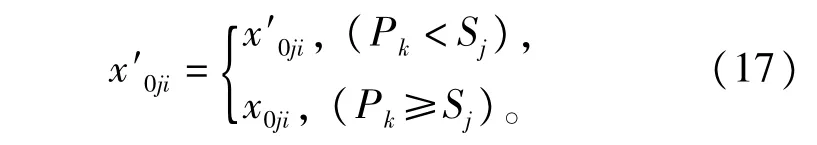
自由搜索算法的终止条件如下∶

2）搜索代数g达到终止代数G∶g≥G；

3）上述条件满足其一。

2.2 自由搜索算法的改进

标准的自由搜索算法是为求取目标函数的最大值作为优化目标而提出的，而本文的预测模型需要使得预测值与实际值的误差越小越好，因此优化目标是求取最小值的。本文将标准自由搜索算法的信息素更新算法修改为如下达到求取最小值的目的∶

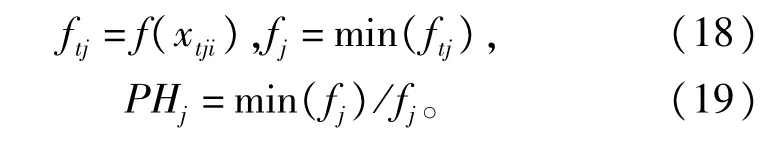
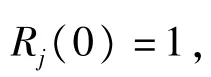
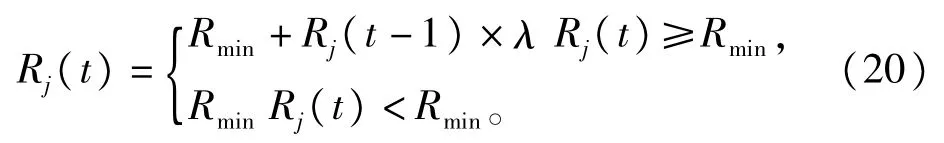
灵敏度参数对于自由搜索算法的性能也有着很大的影响，增大灵敏度，个体将趋近整个群体的当前最佳值进行局部搜索。减小灵敏度，个体可以在其他邻域进行全局搜索。本文对灵敏度进行如下的修改∶

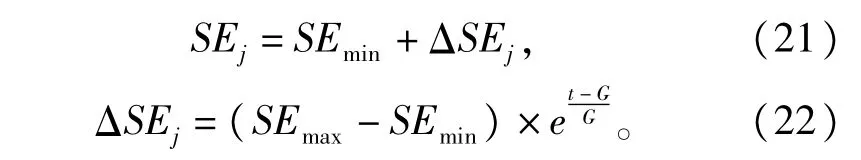
标准算法中灵敏度取值由于随机数导致其具有随机性，而按照本文上面公式进行灵敏度的修改，使算法前期适当减小灵敏度，个体在其他邻域进行全局搜索，算法迭代后期增大灵敏度，使个体趋近于整个种群当前最佳值进行局部搜索，从而提高算法的收敛速度。

综上，本文的改进自由搜索最小二乘支持向量机时延预测模型实现步骤可描述如下∶

步骤1∶初始化

1）设定搜索的初始值∶种群规模M，搜索最大代数G，搜索步长T，待优化参数为γ，σ2，m，输人样本时延序列归一化处理；

2）按式（10）均匀产生初始种群；

3）初始化搜索∶根据初始值生成初始信息素，释放初始信息素，得到初始搜索结果。

步骤2∶搜索

1）按式（21）与式（22）计算灵敏度；

2）按式（11）与式（12）确定新一轮的起始点；

3）将预测模型预测的预测值与时延实际值误差的MSE作为评价指标，其定义如下∶

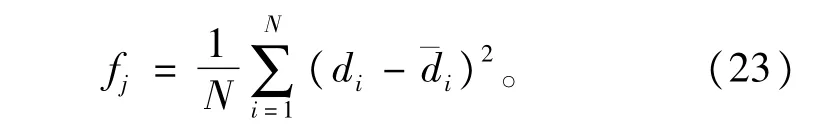
4）按式（18）计算信息素，按照式（19）释放信息素，得到本次搜索结果；

5）选取并保留最佳个体；

6）按式（20）调整搜索半径。

步骤3∶终止判定

判断终止条件，若满足输出最佳优化参数γ，σ2，m；

最优预测模型建立完成后，即可按照第1节的预测步骤进行预测。

3 仿真

利用时延测试软件得到500组时延样本数据，前400组数据用于预测模型的训练，后100组数据用于预测模型精度的验证，为了对比本文改进的自由搜索最小二乘支持向量机的性能，与标准LSSVM算法工具箱中的网格法参数优化，文献［17］中的遗传算法参数优化，文献［18］中的粒子群算法参数优化分别进行了对比。

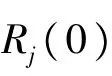
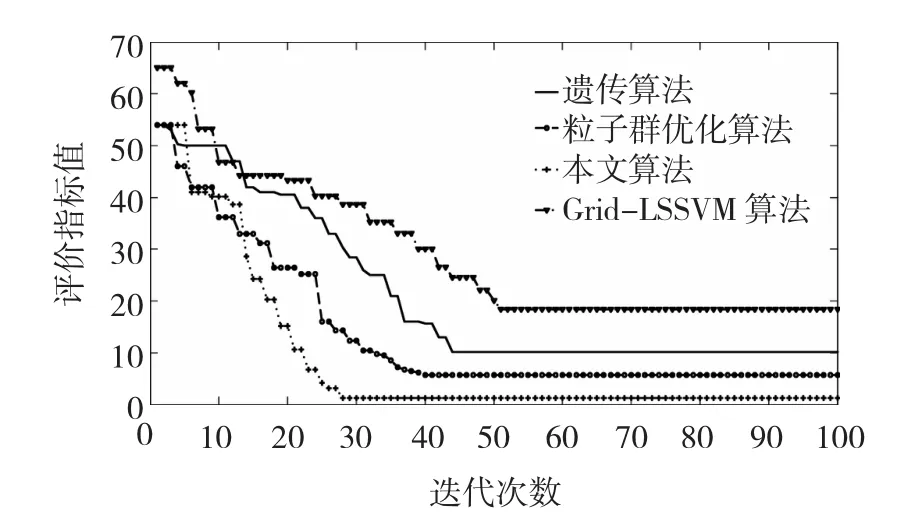
图3 评价指标值变化对比Fig.3 Thecomparisonofevaluationindexvalue

表1为本文IFS-LSSVM、GA-LSSVM、PSO-LSSVM、LSSVM工具箱中网格法寻优后的参数结果。

表1 参数寻优结果Table1 Theresultsofoptimization

图4～图7为4种算法的100组测试数据的实际值与预测值的对比曲线，从这些图中可看出本文的方法的时延预测值较另外3种方法更好的拟合了网络的实际时延，较好的预测了未来时刻时延的变换趋势。

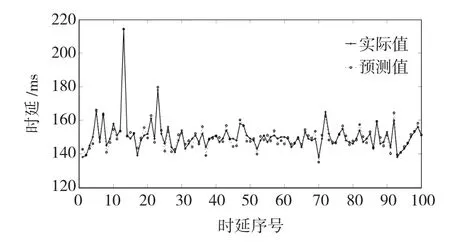
图4 IFS-LSSVM时延预测结果对比Fig.4 Thepredictiveresultcomparisonbased onIFS-LSSVM

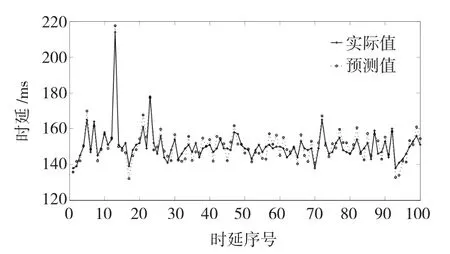
图5 PSO-LSSVM时延预测结果对比Fig.5 Thepredictiveresultcomparison basedonPSO-LSSVM

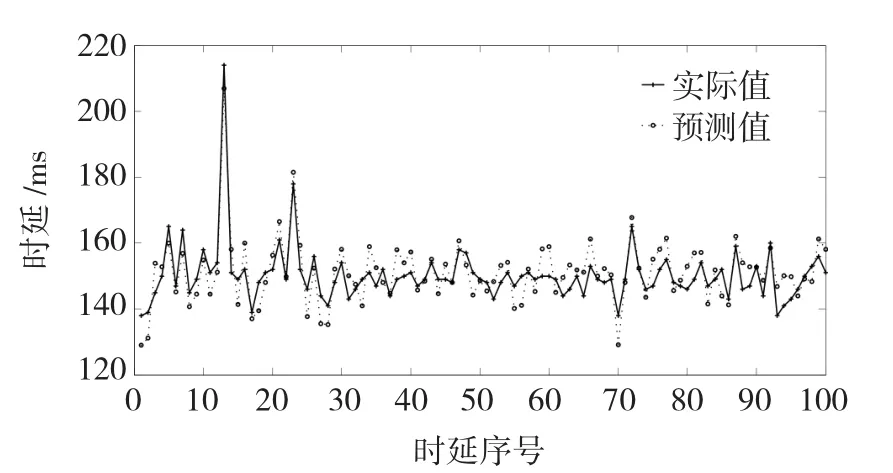
图6 GA-LSSVM时延预测结果对比Fig.6 Thepredictiveresultcomparison basedonGA-LSSVM

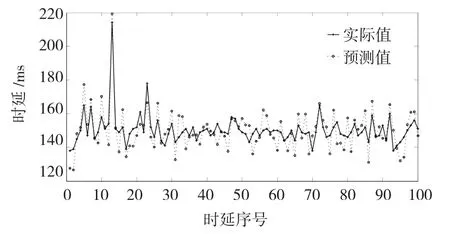
图7 Grid-LSSVM时延预测结果对比Fig.7 Thepredictiveresultcomparison basedonGrid-LSSVM

图8为4种预测方法预测误差的分布图，从图中可看出本文的预测方法的预测误差更小，同时分布更加均匀，其预测误差随着预测时间变长变化幅度要小于其他3种方法，表明本文的预测方法具有更好的预测效果。

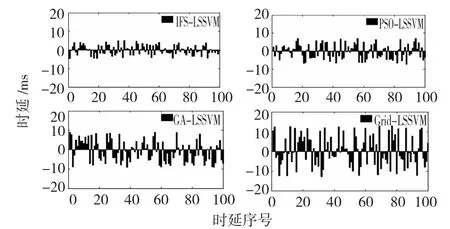
图8 预测误差分布图Fig.8 Thepredictionerrordistribution

为了更进一步的对比预测效果，表2给出了4种算法的MSE与平均绝对百分误差（meanabsolute percentageerror，MAPE）对比。

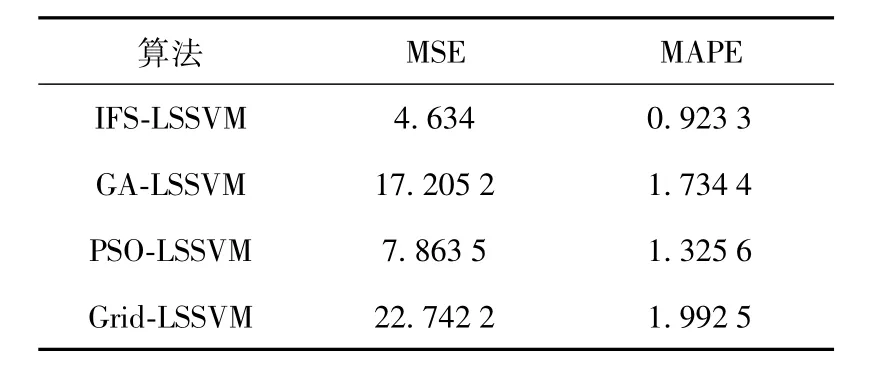
表2 MSE与MAPE指标对比Table2 Theperformancecomparisonof MSEandMAPE

从表2中可看出本文的方法在MSE与MAPE评价指标上优于其他3种预测方法，具有更高的预测精度。

4 结论

LSSVM算法由于自身的优点非常适于非线性时间序列的预测，但是其算法存在参数难以确定的问题。为了实现最优参数的确定，文中提出一种基于改进自由搜索的最小二乘支持向量机（IFS-LSSVM）预测模型，对标准自由搜索算法进行改进使得算法适用于LSSVM的参数优化，对具有强非线性特性的网络时延的预测进行了仿真，验证了本文的IFS-LSSVM预测模型较GA-LSSVM、PSO-LSSVM与网格搜索法优化的LSSVM模型具有更好的预测效果。虽然本文的仿真对象是网络时延序列，但是其他的诸如太阳黑子、股票、交通流量等时间序列的预测问题都可采用本文的方法，未来工作可在其他时间序列问题的预测上进一步验证与修正本文的方法。

∶

［1］DINGSF，HUAXP，YUZJ.Anoverviewonnonparallelhyperplanesupportvectormachinealgorithms［J］.NeuralComputing andApplications，2013，25（5）∶975-982.

［2］SUYKENSJAK，VANDEWALLEJ.Leastsquaressupportvector machinesclassifiers［J］.NeuralProcessingLetters，1999，9（3）∶293-300.

［3］田中大，高宪文，李琨.基于EMD与LS-SVM的网络控制系统时延预测方法［J］.电子学报，2014，42（5）∶868-874. TIANZhongda，GAOXianwen，LIKun.Time-delaypredictionmethodofnetworkedcontrolsystembasedonEMDandLS-SVM［J］.ActaElectronicaSinica，2014，42（5）∶868-874.

［4］田中大，高宪文，史美华，等.资源受限网络控制系统的模糊反馈调度［J］.电机与控制学报，2013，17（1）∶94-101. TIANZhongda，GAOXianwen，SHIMeihua，etal.Fuzzyfeedback schedulingofresourceconstrainednetworkedcontrolsystem［J］. ElectricMachinesandControl，2013，17（1）∶94-101.

［5］HUTJ，HUANGXX，TANQ.Timedelaypredictionforspace teleoperationbasedonnon-Gaussianauto-regressivemodel［C］//2012ProceedingsofInternationalConferenceonModelling，Identification＆Control（ICMIC），June24-26，2012，Wuhan，China.2012∶567-572.

［6］时为国，邵成，孙正阳.基于AR模型时延预测的改进GPC网络控制算法［J］.控制与决策，2012，27（3）∶477-480. SHIWeiguo，SHAOCheng，SUNZhengyang.ImprovedGPCnetwork-controlalgorithmbasedonARmodeltime-delayprediction ［J］.ControlandDecision，2012，27（3）∶477-480.

［7］YANGM，RUJ，LIXR，etal.PredictingInternetend-to-end delay∶amultiple-modelapproach［C］//24thAnnualJointConferenceoftheIEEEComputerandCommunicationsSocieties，March13-17，2005，Miami，USA.2005，4∶2815-2819.

［8］TABIBSRS，JALALIAA.Modellingandpredictionofinternet time-delaybyfeed-forwardmulti-layerperceptronneuralnetwork ［C］//SecondUKSIMEuropeanSymposiumonComputerModelingandSimulation，Sept8-10，2008，Liverpool，England. 2008∶611-616.

［9］RAHMANIB，MARKAZIAHD，MOZAYANIN.Realtimepredictionoftimedelaysinanetworkedcontrolsystem［C］//Proceedingsofthe3rdInternationalSymposiumonCommunications，ControlandSignalProcessing，March12-14，2008，StJulians，Malta.2008∶1242-1245.

［10］SADEGHZADEHN，AFSHARA，MENHAJMB.AnMLPneuralnetworkfortimedelaypredictioninnetworkedcontrolsystems ［C］//ControlandDecisionConference，July2-4，2008，Yantai，China.2008∶5314-5318.

［11］田中大，高宪文，李琨.基于KPCA与LSSVM的网络控制系统时延预测方法［J］.系统工程与电子技术，2013，35（6）∶1281-1285. TIANZhongda，GAOXianwen，LIKun.Networkedcontrolsystemtimne-delaypredictionmethodbasedonKPCAandLSSVM ［J］.SystemsEngineeringandElectronics，2013，35（6）∶1281-1285.

［12］李春茂，肖建，张玥.基于LS-SVM的网络化控制系统自适应预测控制［J］.系统仿真学报，2007，19（155）∶3494-3498. LIChunmao，XIAOJian，ZHANGYue.Approachofadaptive predictioncontrolonnetworkedcontrolsystemsbasedonleastsquaressupportvectormachines［J］.JournalofSystemSimulation，2007，19（155）∶3494-3498.

［13］杨晓冬，王崇林，史丽萍.H桥逆变器IGBT开路故障诊断方法研究［J］.电机与控制学报，2014，18（5）∶112-118. YANGXiaodong，WANGChonglin，SHILiping.StudyofIGBT open-circuitfaultdiagnosismethodforH-bridgeinverter［J］.E-lectricMachinesandControl，2014，18（5）∶112-118.

［14］龚瑞昆，宁荣飞，陈磊，等.改进DOAS技术在混合气体中的定量分析 ［J］.哈尔滨理工大学学报，2012，17（6）∶110 -113. GONGRuikun，NINGRongfei，CHENLei，etal.Improvmentof DOAStechnologyintheapplicationofmixedgasquantitativea-nalysis［J］.JournalofHarbinUniversityofScienceandTechnology，2012，17（6）∶110-113.

［15］YANGKH，ZHAOLL.Anewoptimizingparameterapproach ofLSSVMmulticlassclassificationmodel［J］.NeuralComputing andApplications，2012，21（5）∶945-955.

［16］KALINP，GUYL.FreesearchacomparativeAnalysis［J］.InformationScience，2005，172∶173-193.

［17］张弦，王宏力.嵌人维数自适应最小二乘支持向量机状态时间序列预测方法 ［J］.航空学报，2010，31（12）∶2309 -2313. ZHANGXian，WANGHongli.Conditiontimeseriesprediction usingleastsquaressupportvectormachinewithadaptiveembeddingdimension［J］.ActaAteronauticaAstronauticaSinica，2010，31（12）∶2309-2313.

［18］尚万峰，赵升吨，申亚京.遗传优化的最小二乘支持向量机在开关磁阻电机建模中的应用［J］.中国电机工程学报，2009，29（12）∶65-69. SHANGWanfeng，ZHAOShengdun，SHENYajing.Application ofLSSVMoptimizedbygeneticalgorithmtomodelingofswitched reluctancemotor［J］.ProceedingsoftheCSEE，2009，29（12）∶65-69.

（编辑∶张诗阁）

IFS-LSSVManditsapplicationintime-delayseriesprediction

TIANZhong-da1，LIShu-jiang1，WANGYan-hong1，GAOXian-wen2
（1.CollegeofInformationScienceandEngineering，ShenyangUniversityofTechnology，Shenyang110870，China；2.CollegeofInformationScienceandEngineering，NortheasternUniversity，Shenyang110819，China）

∶Itisdifficulttodeterminetheoptimalparametersofleastsquaressupportvectormachinepredictionmodel，soapredictionmethodbasedonimprovedfreesearchalgorithm（IFS-LSSVM）wasproposedtodeterminetheoptimalparametersofleastsquaressupportvectormachines.First，thestandard freesearchalgorithmwasimprovedsothatitcanbeappliedtotheparameteroptimizationofleastsquares supportvectormachines，theimprovedharmonysearchalgorithmhasbetteroptimizationperformance. Thentheleastsquaressupportvectormachineswasappliedtopredictthetime-delayseriesofthenetwork basedonimprovedfreesearchoptimizationalgorithm.Finally，time-delayserieswasusedasprediction simulationobject，geneticalgorithmoptimizedleastsquaressupportvectormachines（GA-LSSVM），particleswarmoptimizationalgorithmoptimizedleastsquaressupportvectormachines（PSO-LSSVM），standardgridsearchmethodofleastsquaressupportvectormachines（Grid-LSSVM）toolboxwerecompared.Simulationcomparisonresultsshowthattheproposedmethodhashigherpredictionaccuracyand smallerpredictionerror.

∶leastsquaressupportmachines；freesearch；time-delayseries；prediction；timeseries

∶TP393

∶A

∶1007-449X（2015）11-0104-07

∶2013-12-12

∶国家自然科学基金（61034005）；辽宁省博士科研启动基金（20141070）

∶田中大（1978—），男，博士，讲师，研究方向为混沌时间序列预测、网络控制系统；

李树江（1966—），男，博士，教授，研究方向为复杂工业过程建模与控制；

王艳红（1967—），女，博士，教授，研究方向为生产过程调度与优化控制；

高宪文（1955—），男，博士，教授，博士生导师，研究方向为复杂工业过程建模与控制。

∶田中大

DOI∶10.15938/j.emc.2015.11.016