自适应CKF强跟踪滤波器及其应用

丁家琳，肖建，赵涛（.西南交通大学电气工程学院，四川成都 6003；.西南交通大学交通运输与物流学院，四川成都 6003）

自适应CKF强跟踪滤波器及其应用

丁家琳1，肖建1，赵涛2
（1.西南交通大学电气工程学院，四川成都 610031；2.西南交通大学交通运输与物流学院，四川成都 610031）

∶针对强跟踪滤波器（STF）的理论局限以及基于UT变换的强跟踪滤波器（UTSTF）处理高维非线性系统时滤波精确度下降甚至发散等问题，提出一种基于容积卡尔曼滤波（CKF）算法的强跟踪滤波器（CKFSTF）。CKFSTF兼具了STF和CKF的优点∶鲁棒性强，滤波精度高，数值稳定性好，计算速度快，容易实现且应用范围广。此外，对于目标跟踪系统过程噪声统计特性未知的情况，在CKFSTF的基础上应用Sage-Husa噪声估值器对噪声统计特性进行在线估计，形成自适应CKFSTF。仿真结果验证了新算法的有效性。

∶强跟踪滤波器；容积卡尔曼滤波；自适应性；目标跟踪

0 引言

由于实际应用系统的复杂性与时变性，非线性系统状态和参数的估计一直受到广泛的关注。为了能对系统实现精确的控制，众多学者进行了大量的研究工作并提出了许多经典的非线性滤波算法。其中，扩展卡尔曼滤波器（extendKalmanfilter，EKF）因其算法简单、收敛速度快等优点得到了广泛的应用。遗憾的是EKF关于模型不确定的鲁棒性较差，此外，在系统达到平稳状态时，EKF将丧失对突变状态的跟踪能力。为此，文献［1］提出了一种带次优渐消因子的扩展卡尔曼滤波器，即强跟踪滤波器（strongtrackingfilter，STF）［2］，以避免由模型不确定而引起的鲁棒性差、滤波发散等问题，并且对系统状态的突变具有很强的跟踪能力［3］。由于STF是在EKF的基础上进行改进得到的，所以仍然存在一些自身无法克服的问题，如∶对于强非线性系统，线性化会产生较大的估计误差，甚至使得滤波发散；要求非线性系统模型连续可微，且需要计算非线性模型的雅可比矩阵等。为此，文献［4］和文献［5］分别提出了基于Unscented变换和中心差分变换的强跟踪滤波器。该方法通过对非线性高斯系统状态的后验均值和协方差进行逼近，避免了雅可比矩阵的计算，且有效的提高了滤波精度。

但由于无迹卡尔曼滤波器（unscentedKalman filter，EKF）和中心差分滤波器（centraldifference Kalmanfilter，CDKF）的性能易受参数取值的影响，仅适用于解决低维（n＜3）的非线性滤波问题，在状态维数较高时会出现滤波性能不佳甚至发散现象［6-8］。而基于UKF和CDKF的强跟踪滤波器也因此存在相同的问题。为了克服上述缺点，Arasaratnam等人［6］基于球面径向规则采用一组等权值的容积点来逼近系统状态的后验分布，提出了容积卡尔曼滤波（cubatureKalmanfilter，CKF）。由于CKF在滤波过程中其权值始终为正，从而保证了协方差的正定性，所以适用于解决从低维到高维的非线性滤波问题，具有更广的应用范围。虽然UKF 与CKF有着相似的计算复杂度，由于UKF可看作二阶EKF的特殊形式，经过非线性传递后UT变换不能总保存一阶和二阶矩信息［9］，而CKF比UKF能更精确的保存一阶和二阶矩信息，所以CKF有着更高的滤波精确度和数值稳定性［8，10］。由于这些显著的优点，近年来CKF也得到了广泛的应用［11］。考虑到在目标跟踪系统中，量测噪声的统计特性一般可以事先由传感器的物理特性得到，而过程噪声由于人为有意识的操作和外界干扰等，使它的统计特性往往是未知或时变的［12］，如果将不准确的噪声统计特性应用到滤波过程中，可能会导致较大的估计误差甚至滤波发散等。

为此，本文提出一种带Sage-Husa噪声统计估值器的CKF强跟踪滤波器（CKFSTF）。该方法能兼具上述改进强跟踪滤波器的优点，又能克服高维情况下存在滤波性能不佳甚至发散等现象，且具有更优的计算速度和数值稳定性，通过对未知噪声统计特性的在线估计和修正，增强滤波器应对噪声统计特性变化的自适应能力。

1 基于CKF的强跟踪滤波器

1.1 强跟踪滤波理论

考虑如下非线性离散动态系统

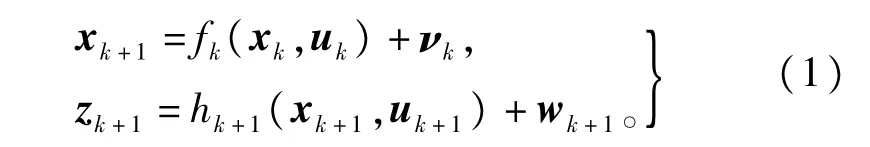
式中∶xk∈Rn是系统的状态向量；uk∈Rm是已知的控制输人；zk∈Rp是系统的观测向量；函数fk∶Rn× Rm→Rn和hk∶Rn×Rm→Rp分别为已知的非线性函数；vk∈Rn和wk∈Rp是带时变均值和协方差且线性无关的高斯白噪声。

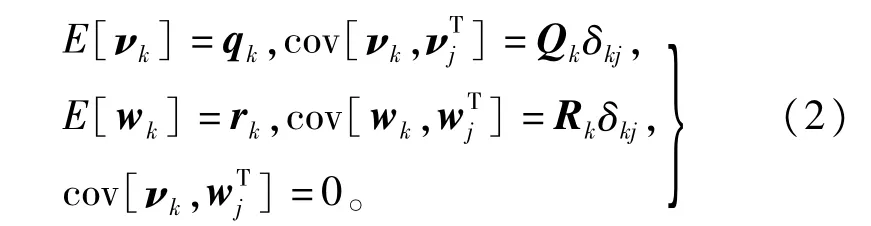
式中，δkj为Kronecher-δ函数。初始状态x0服从高斯分布N（xˆ0，P0），且与vk和wk互不相关。

为了增强滤波器关于系统模型不确定的鲁棒性以及系统状态突变的跟踪能力，周东华等人在EKF的基础上提出了强跟踪滤波器的概念。基本思想是选择一个适当的时变增益矩阵Kk+1，使得［1］

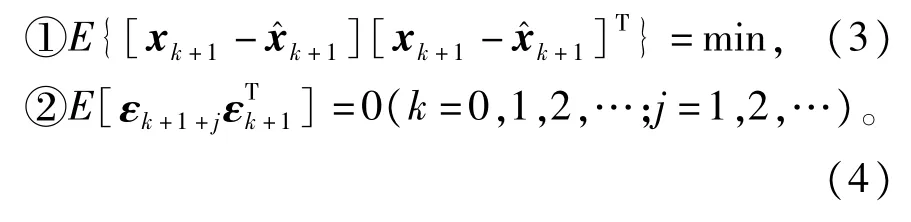
其中，εk+1=zk+1-zˆk+1｜k。条件①为EKF的性能指标，条件②要求不同时刻的残差序列处处保持相互正交。但在实际系统中，由于模型的不确定使得滤波器的状态估计值偏离真实值，从而造成输出残差序列不再正交。为了保持强跟踪滤波器的优良特性，在预测状态误差协方差阵中引人次优渐消因子，通过在线调整增益阵，强迫残差序列仍然保持相互正交，从而保证滤波器对实际系统状态的跟踪，算法的具体步骤为［1］

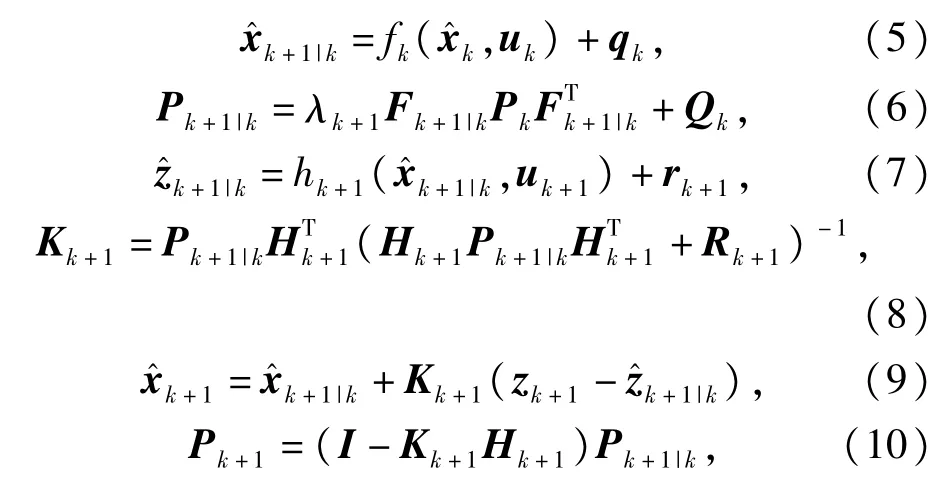
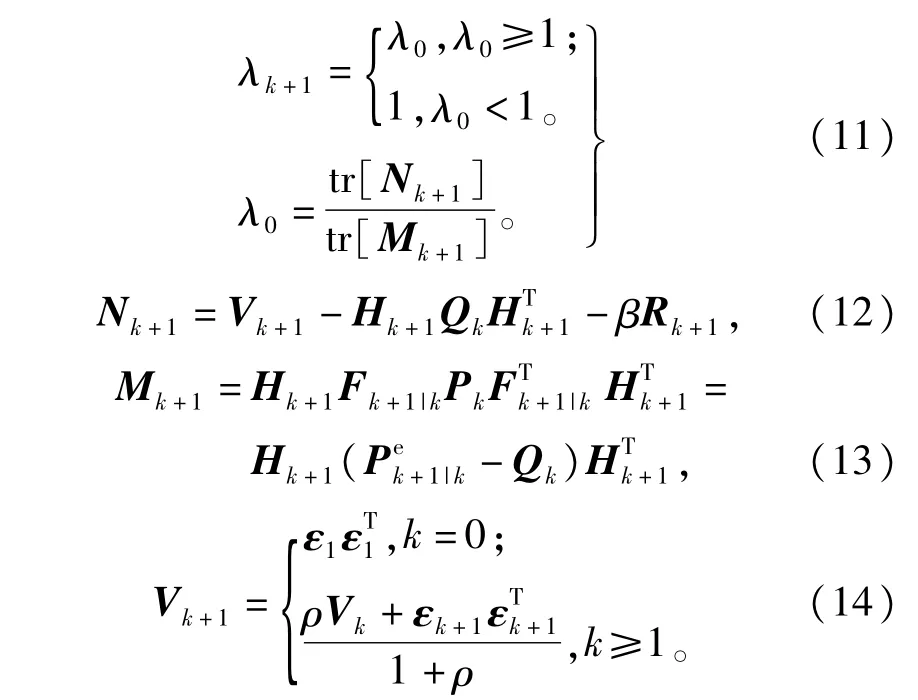
其中

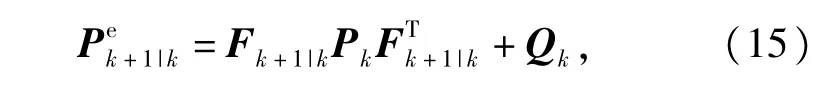
表示未引人渐消因子的状态预测协方差阵。0＜ρ≤1为遗忘因子，一般取ρ=0.95［13］。β≥1为一个选定的弱化因子，加人弱化因子是目的是避免有可能造成的过调节，使得状态估计值更加平滑，此数值可凭经验选定，这里我们取β=4.5。

1.2 基于CKF的强跟踪滤波理论

CKF与UKF、CDKF同属确定采样型滤波，至少能以二阶泰勒精度逼近非线性高斯状态的后验分布，所以估计精度均高于EKF且能有效克服EKF的理论局限。但UKF和CDKF受参数取值的影响使其仅适用于处理低维（n＜3）的非线性状态估计问题，在高维情况下CKF的估计精度和数值稳定性都优于UKF［6-8］。另一方面，尽管UKF与CKF有着相似的计算复杂度，但在每次采样过程中CKF都比UKF少一个采样点，所以计算速度更快，实时性更好。因此考虑将CKF与强跟踪滤波器结合，根据强跟踪滤波器的思想，在CKF的状态预测协方差矩阵中引人时变渐消因子，得到CKF强跟踪滤波器（CKFSTF）。具体分析如下∶

由标准CKF算法步骤有∶

1）初始化

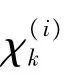
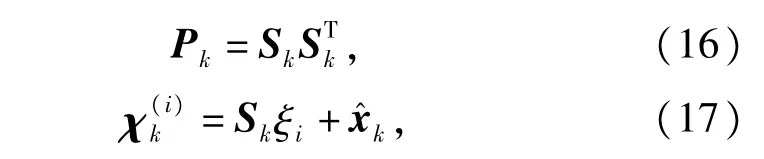
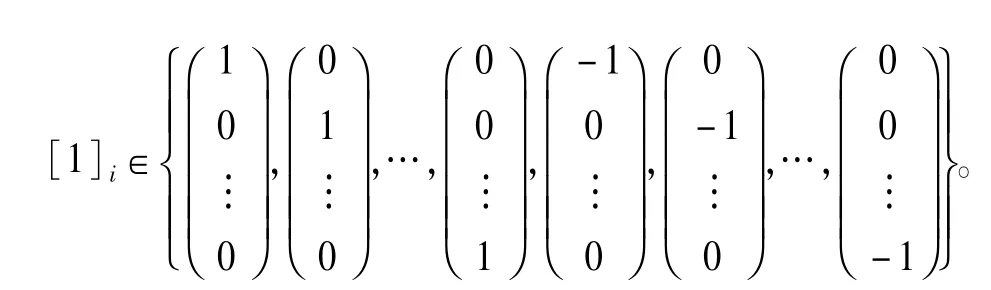
2）预测更新

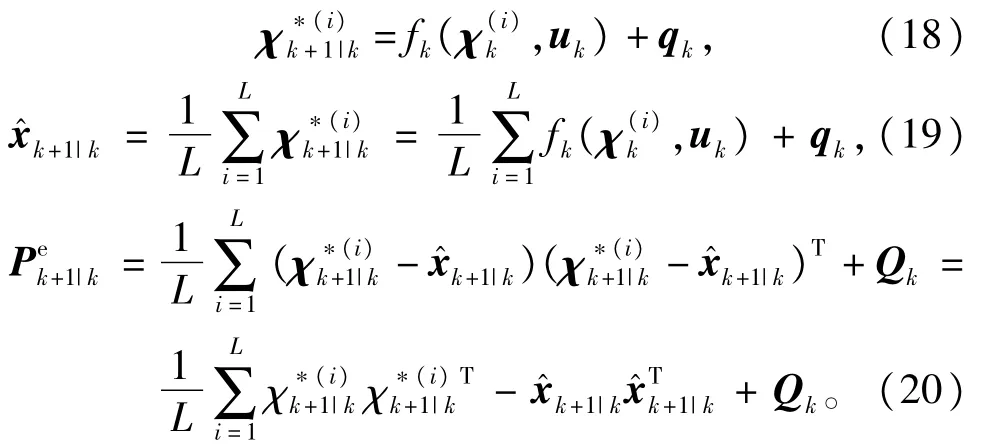
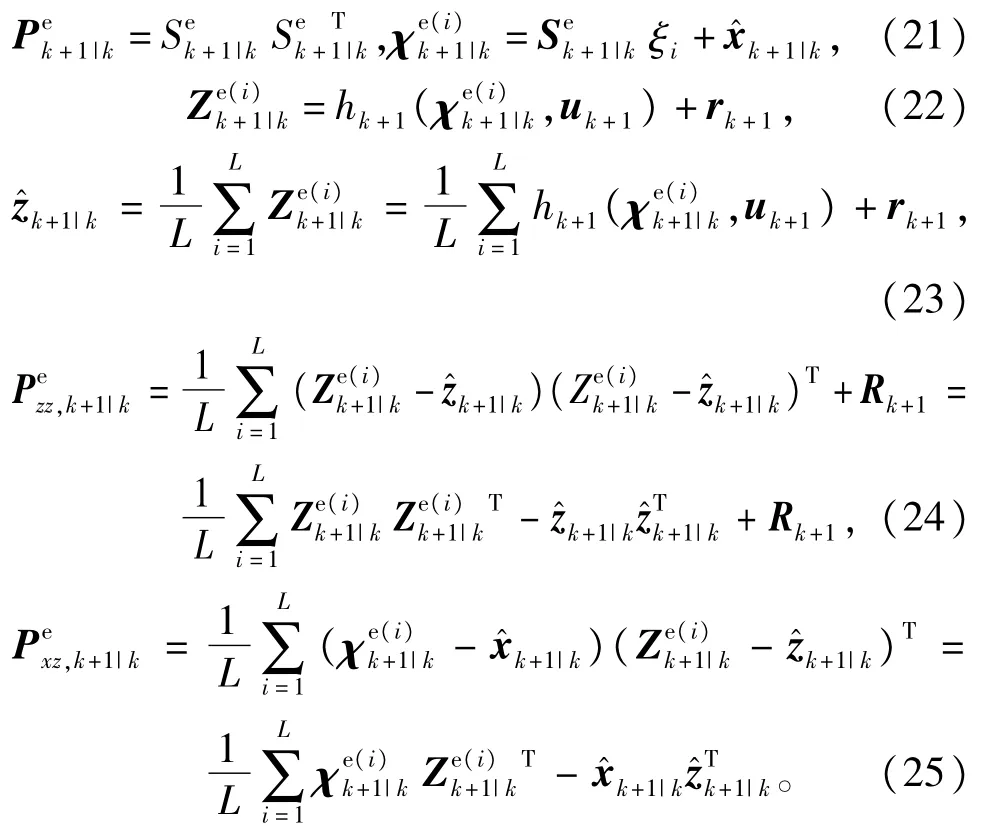
3）状态更新

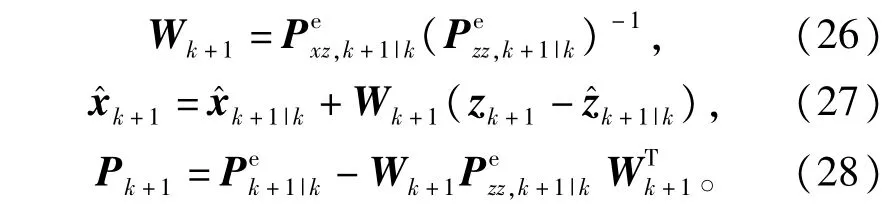
根据强跟踪滤波器的思想，要避免由模型不确定而引起的鲁棒性差、滤波发散等问题，并且对系统状态的突变具有很强的跟踪能力，应对误差协方差阵和相应的增益矩阵进行在线调整，使得输出残差序列保持相互正交，因此需要在状态预测协方差阵中引人时变渐消因子λk+1，即

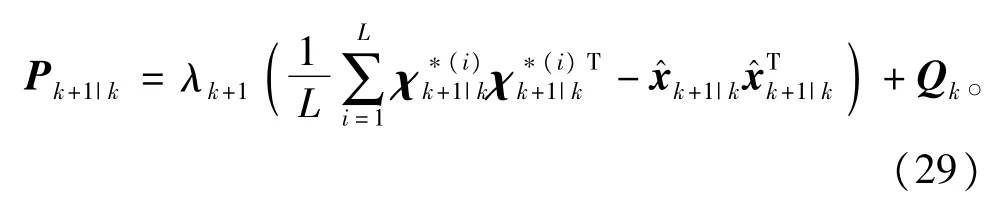
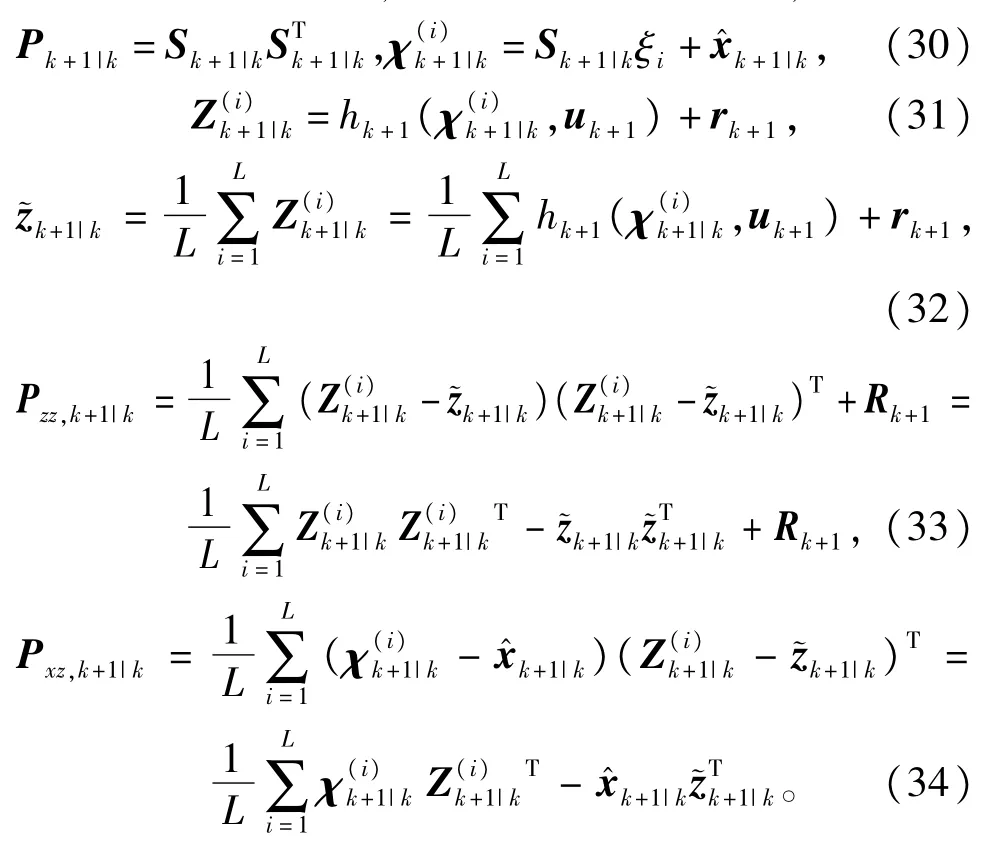
再根据步骤3），即可得到调整后的增益矩阵进而对状态和误差协方差阵进行更新有

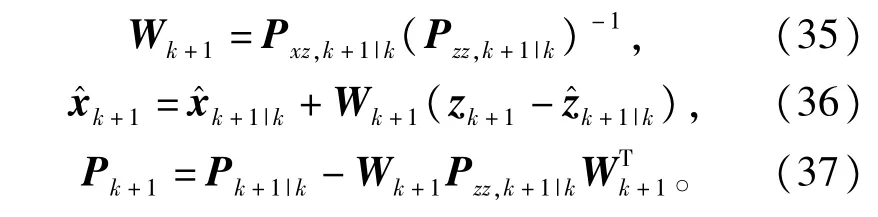
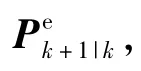
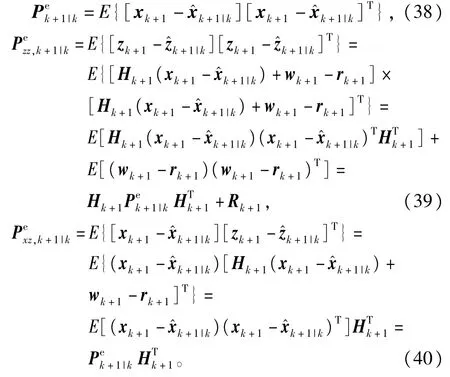
所以有

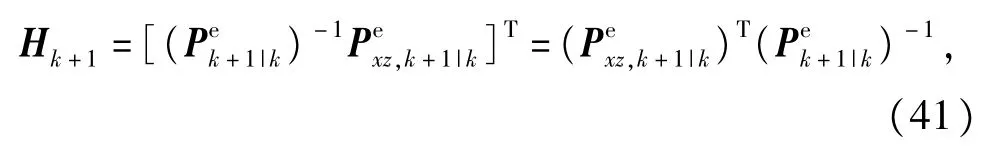
将式（39）和式（40）代人式（12）和式（13），则Nk+1和Mk+1可按下式计算得到

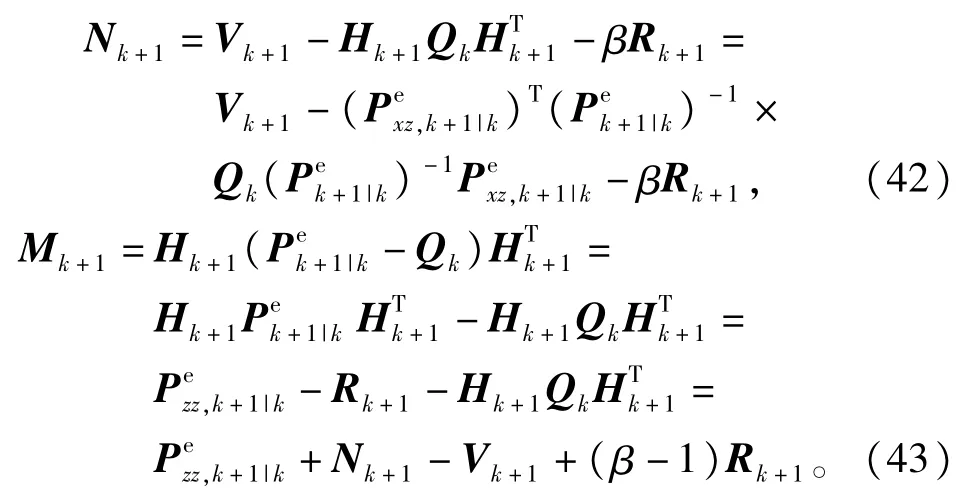
同理，对于引人渐消因子λk+1后的状态预测协方差阵Pk+1｜k，输出预测协方差阵Pzz，k+1｜k和交叉协方差阵Pxz，k+1｜k也可以推导出类似式（39）和式（40）的表示为

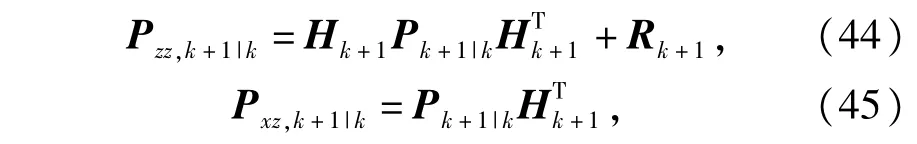
则有

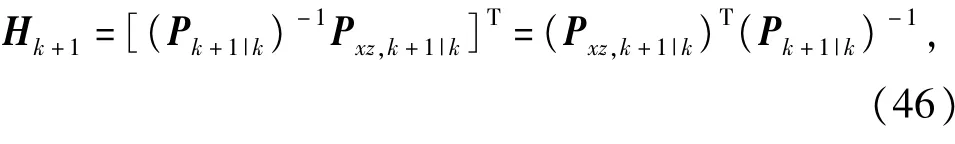
于是将式（45）和式（46）代人式（8）和式（10），可得

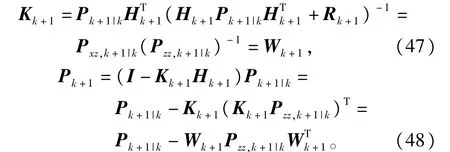
显然，式（47），式（48）与式（35），式（37）是一致的，由此也进一步说明上述的等价表示是可行的。所以在CKFSTF算法中，可以利用式（42）～式（43）在避免求取雅可比矩阵的情况下计算时变渐消因子λk+1，进而实现对状态预测协方差阵的在线调整。

CKFSTF既能保持强跟踪滤波器关于模型不确定的鲁棒性以及对系统状态突变的跟踪能力，并且无需计算雅可比矩阵，还具备更高的滤波精确度和数值稳定性，适用于解决从低维到高维的非线性滤波问题。考虑到在实际应用中系统的噪声统计特性往往是未知或时变的，若利用不准确的噪声统计特性可能会导致滤波精确度降低甚至使得滤波发散。因此要保持CKFSTF的滤波性能，增强滤波器应对噪声统计特性变化的自适应能力是非常重要的。

2 自适应CKF强跟踪滤波算法

2.1 Sage-Husa过程噪声自适应估计算法

对于系统的过程噪声统计特性未知或时变的情况，为了能以较高的滤波精度实现对系统状态稳定的跟踪，需要对未知或时变的噪声统计特性进行实时估计和修正，使得滤波器对噪声统计特性的变化具有鲁棒性。而Sage-Husa自适应滤波算法因其计算简单，原理清晰，可同时估计出噪声的一、二阶矩被广泛的应用［15］。

对于非线性系统（1），我们假设系统过程噪声的均值q=0，结合EKF与Sage-Husa自适应滤波算法，可得到时变过程噪声统计特性的递推估计为［14］

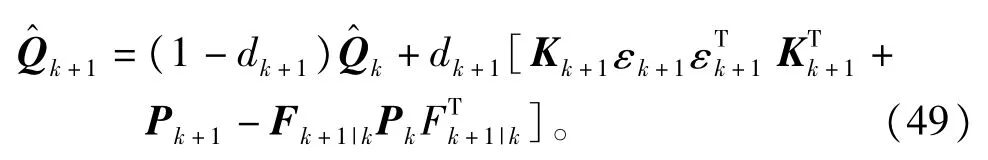
其中，dk+1=（1-b）/（1-bk+1），0＜b＜1为遗忘因子，其值要经实验确定，一般取0.95～0.99。

在CKFSTF滤波过程中，对噪声统计特性进行在线估计时，为避免求取雅可比矩阵所以同样需要对Fk+1｜k和Hk+1进行等价代换，如前一节所述利用式（15），则式（49）可表示为

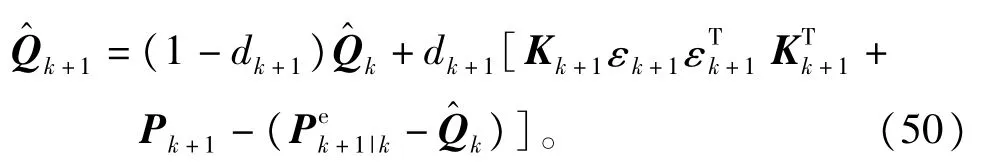
再利用式（47）的等价表示以及式（20）可得到自适应CKFSTF中时变噪声统计特性的递推估计为

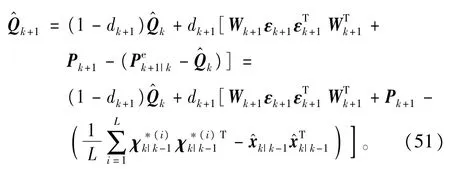
将式（51）嵌人到CKFSTF算法，即式（16）～式（37），进行交替运算则构成自适应CKFSTF算法。

2.2 防止滤波发散的改进算法

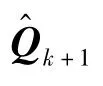
根据式（49）的推导可知，噪声协方差阵的无偏估计是对在对初始的有偏估计方程进行了修正得到的，因此要保证协方差阵的半正定或正定性，可采用噪声协方差阵初始的有偏估值器，即

采用有偏的噪声协方差估值器可以完全阻止滤波器的发散，但可能会造成较大的估计误差，因此在该方法的基础上稍加改进，其计算公式为

算法1∶自适应CKFSTF算法

fork=1，2，…，do

预测更新∶

状态预测协方差阵的在线调整∶

根据式（42）～式（43），由式（11）得到时变渐消因子λk+1，对状态预测协方差阵进行修正

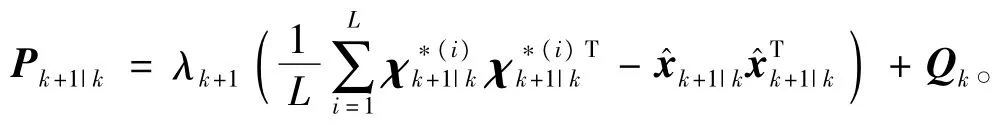
测量更新∶

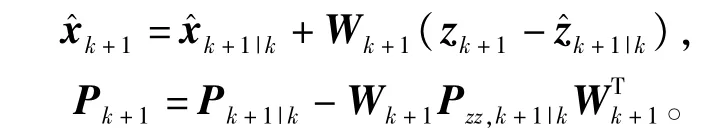
递推估计系统噪声统计特性∶

3 仿真分析和比较

3.1 实例1

考虑如下不连续不可微的非线性离散系统

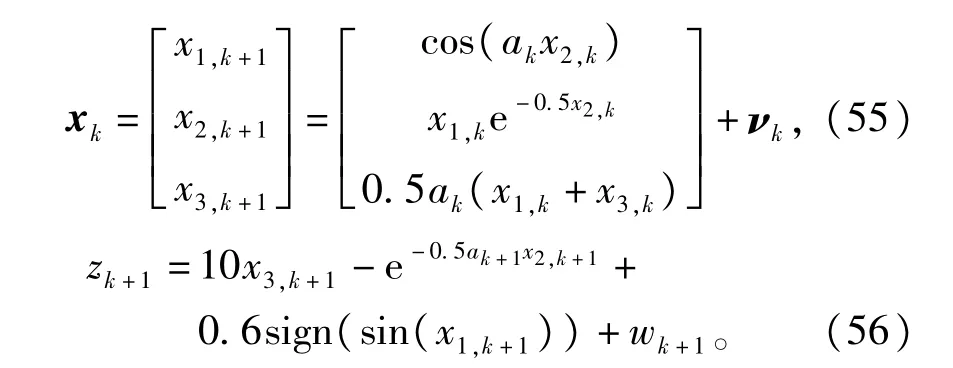
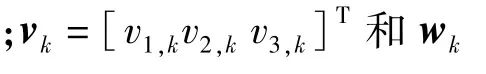
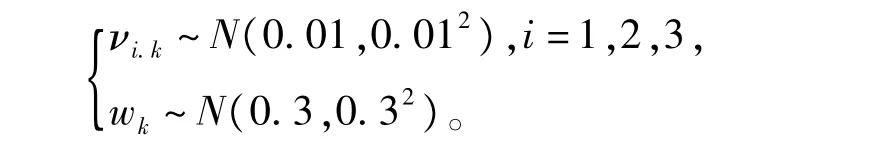
显然，由式（56）可知非线性系统的量测函数是不连续不可微的，因此STF将不再适用。下面我们将采用本文所提出CKFSTF算法对非线性系统式（55）～式（56）的状态以及参数进行估计，验证其算法的有效性。假设系统状态的理论初始值为

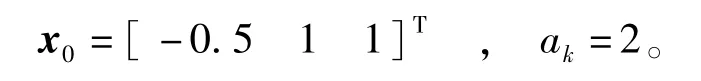
由于存在未知参数，所以系统的模型参数需要与状态进行同时估计，对系统状态进行扩维处理有

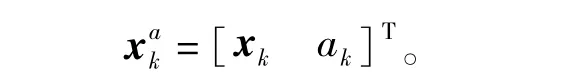
而对应于参数估计的噪声va，k～N（0.01，0.012）。取系统状态估计和误差协方差阵的初始值为

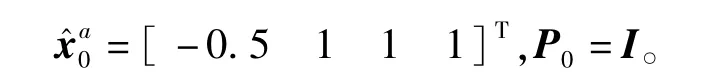
由前面的理论分析可以得知，对式（55）和式（56）这样不连续不可微非线性系统的状态估计问题STF已失效，并在仿真研究中也得到了验证。而由图1可知，CKFSTF算法能有效的处理此类问题，并且系统的状态估计与参数估计是并行进行的。仔细分析图1可看出，在滤波过程的初始阶段，由于模型参数ak的不准确，使得状态估计产生较大的估计误差。但随着模型参数ak对真实值的逐步逼近，系统状态的估计误差也在逐渐减小；而且大致能在15s以后，模型参数ak的估计值开始准确跟踪上真实值，此时系统状态的估计误差也近似于零。由此也说明了在模型参数未知或不准确的情况下，CKFSTF能有效的对不连续不可微非线性系统的状态进行准确的跟踪，它具有较强的关于模型不确定的鲁棒性。

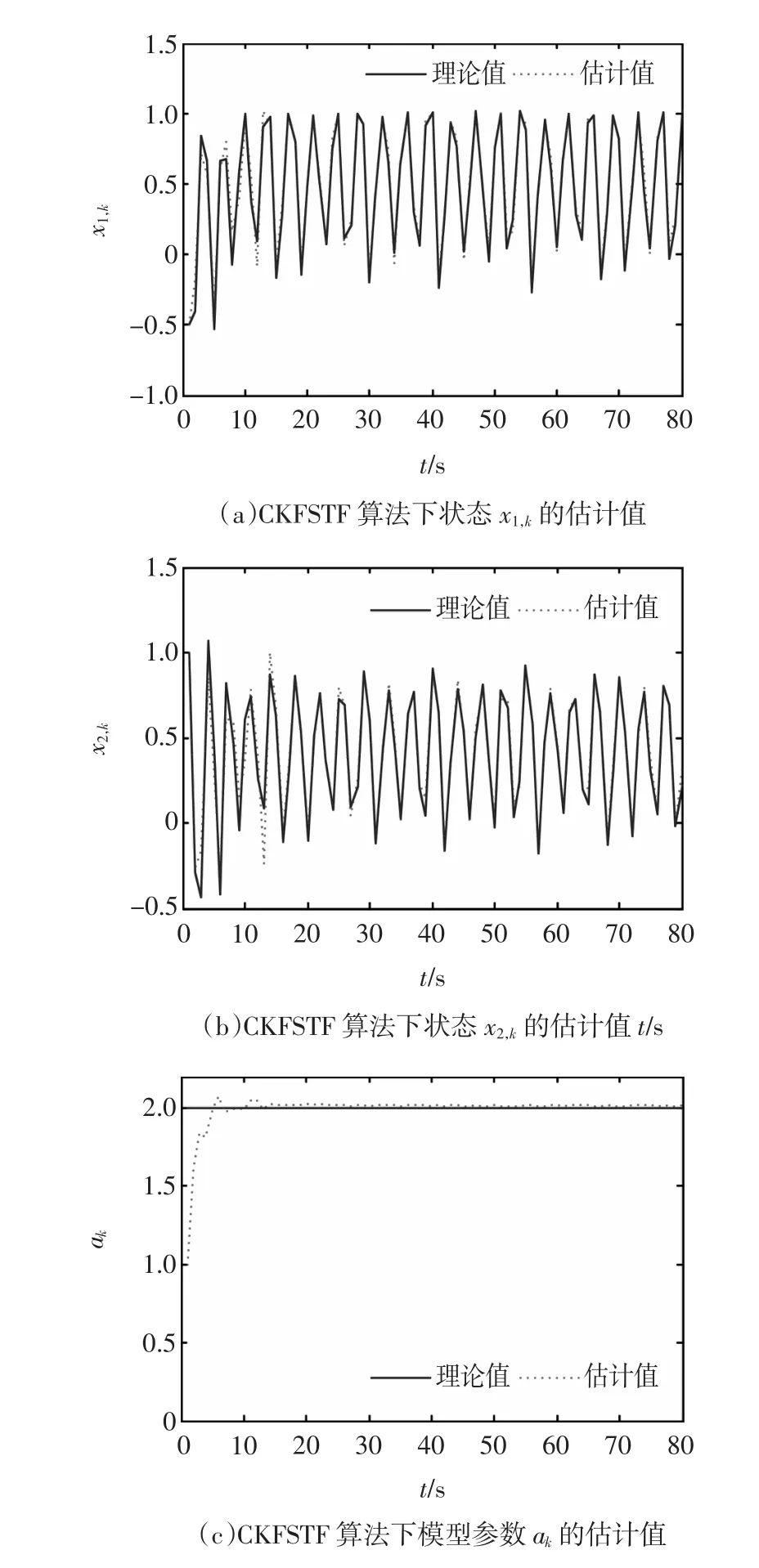
图1 CKFSTF算法下状态及模型参数的估计值Fig.1 Estimationsofstateandparameterin CKFSTFalgorithm

3.2 目标跟踪

考虑典型的空中交通管制情况，飞行器以一未知角速度在水平面内执行机动转弯，其旋转运动的动力学模型可由如下非线性方程描述为

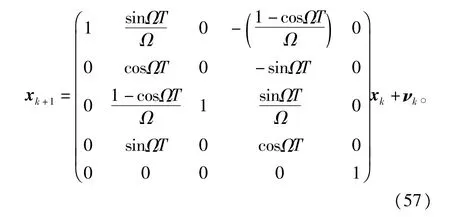
式中∶飞行器的状态x=［ξ.ξ η.η Ω］T；ξ和η表示位置，.ξ和.η分别表示飞行器在x方向和y方向的速度；T是两次量测的时间间隔。雷达固定在飞行器的初始位置，对飞行器的飞行距离r以及方位角θ进行测量，那么量测方程可表示为

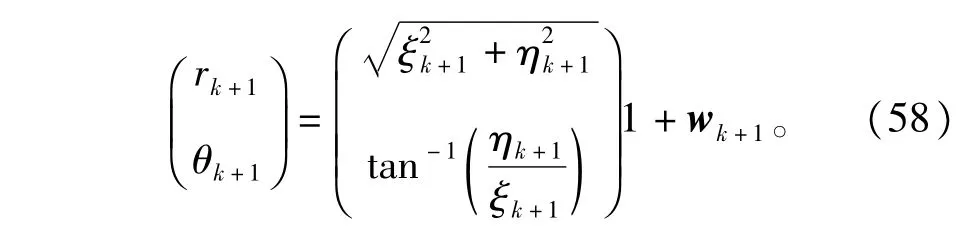
情况1∶系统的噪声统计特性精确已知，且满足∶过程噪声vk～N（0，Q），量测噪声wk～N（0，R），其中

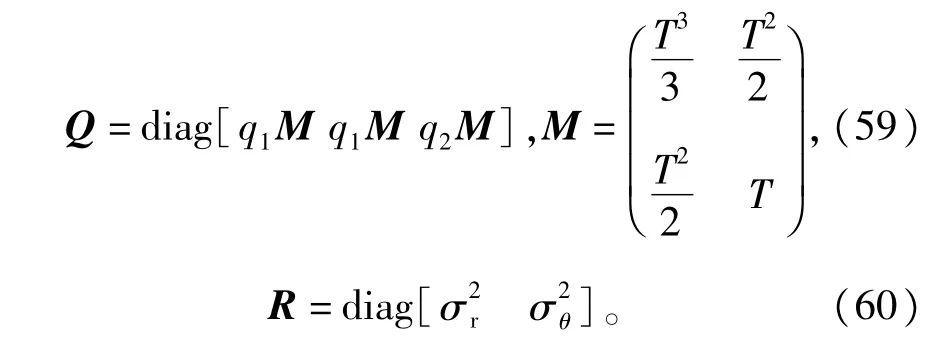
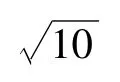
系统状态的理论初始值为

状态估计的初始值xˆ0从分布N（x0，P0）中随机选取，进行100次MonteCarlo仿真，每次仿真的步数为80。分别采用本文所提出的CKFSTF算法、UTSTF算法以及STF对系统状态进行估计。对于UKF的参数选择为α=1e-3，β=2，κ=-2。定义均方根误差（Rootmeansquareerror，RMSE），即

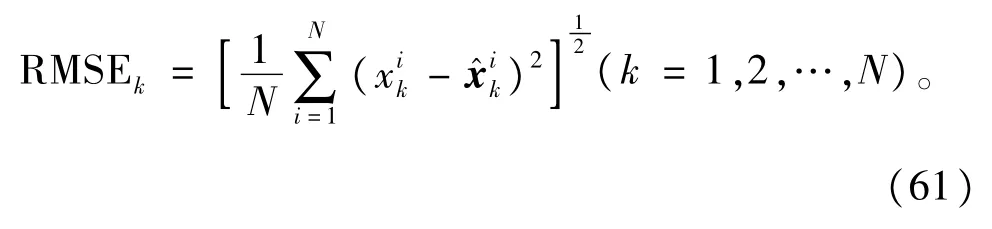
其中，N为MonteCarlo仿真次数。通过均方根误差定量的比较3种算法的性能。

图2、图3和图4分别为采用CKFSTF算法、基于UT变换的强跟踪算法以及STF进行状态估计时位置、速度和角速度的均方根误差曲线比较。表1给出了在进行100次MonteCarlo仿真后，3种算法进行单次MonteCarlo仿真所用的平均计算时间。

从仿真结果可看出，CKFSTF的滤波效果明显优于UKF强跟踪滤波器和STF。说明在处理高维非线性系统状态变化的估计问题时，CKFSTF能有效克服其他强跟踪滤波器所出现的滤波精度不佳甚至滤波发散等现象，正与前面分析的一致。对于计算时间，由于CKF和UKF采样相同的滤波框架，且CKF比UKF少一个采样点，理论上CKF强跟踪滤波器要比UKF强跟踪滤波的计算速度更快，表1的仿真结果也验证了该理论分析的正确性。

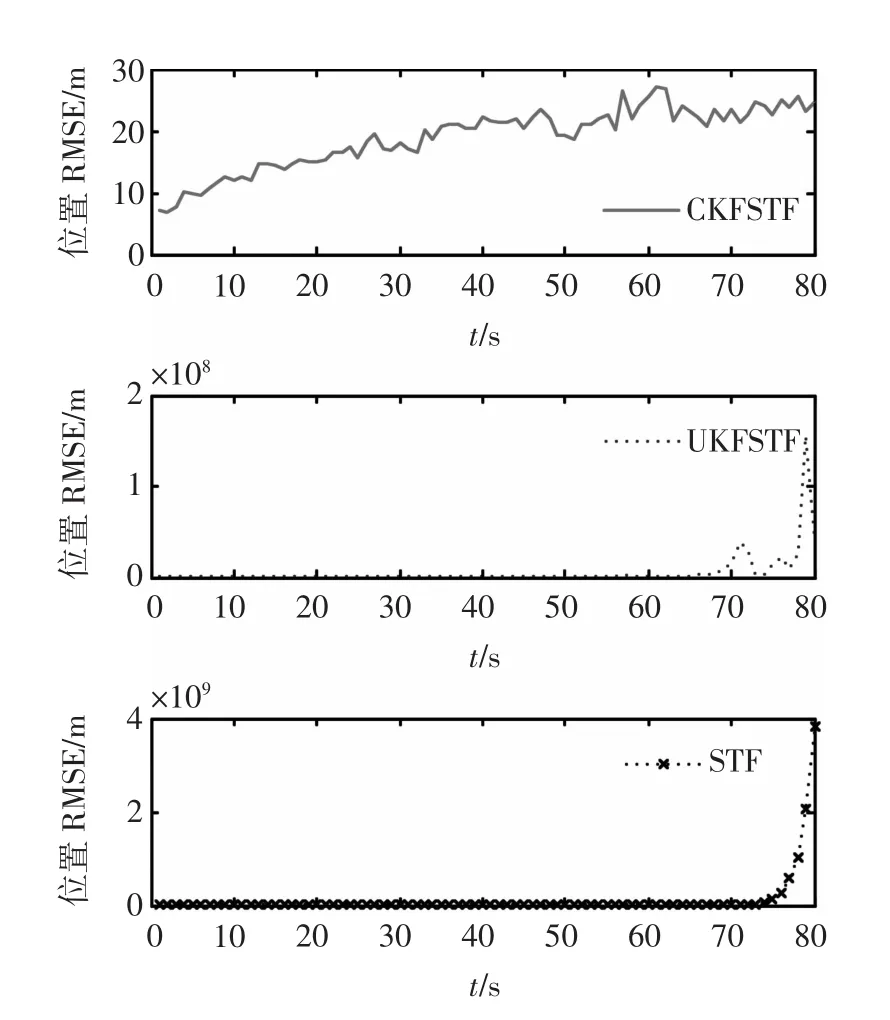
图2 3种算法下位置的均方根误差Fig.2 RMSEsofpositioninthreealgorithms

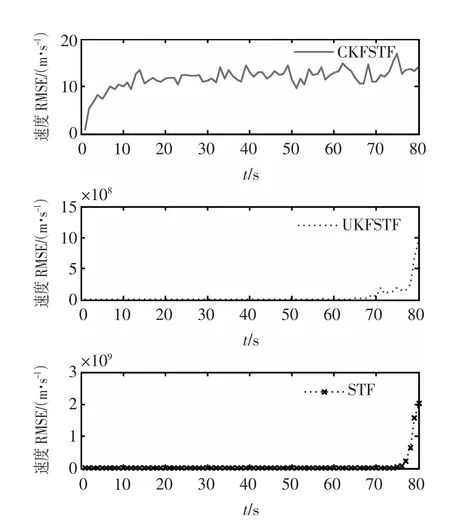
图3 3种算法下速度的均方根误差Fig.3 RMSEsofvelocityinthreealgorithms

表1 3种算法下进行单次MonteCarlo仿真的平均计算时间Table1 AveragecalculationtimesofsingleMonte Carlosimulationinthreealgorithms

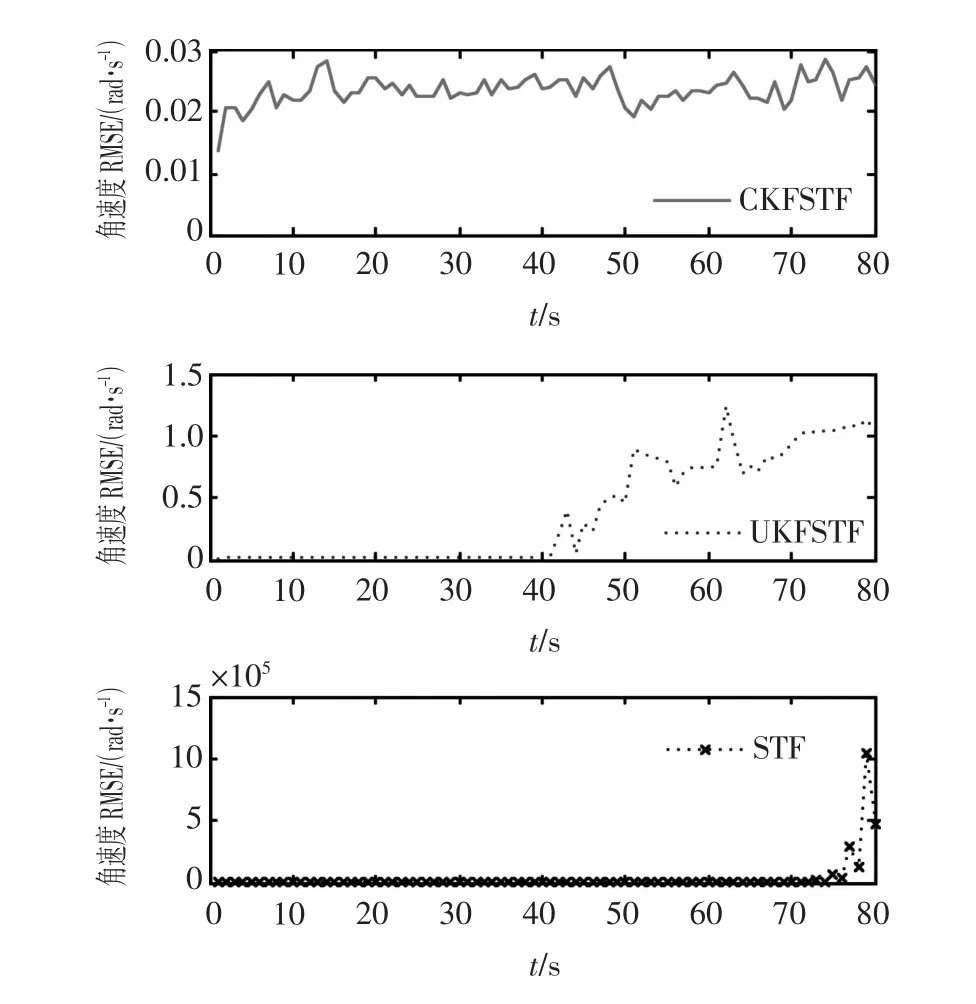
图4 3种算法下角速度的均方根误差Fig.4 RMSEsofangularvelocityinthreealgorithms

情况2∶系统过程噪声的统计特性未知或时变。

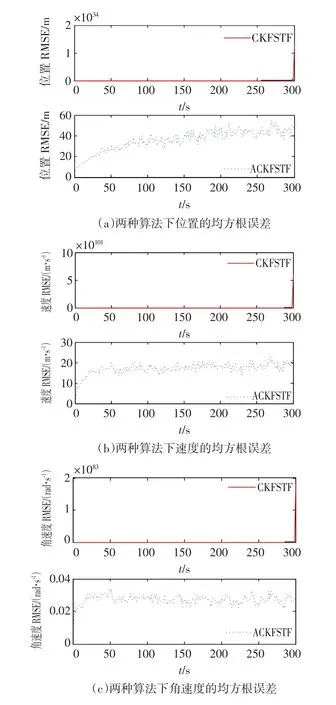
从图6和图7的仿真结果得知，通过自适应CKFSTF所得到的速度、角速度均方误差小于CKFSTF的均方误差，而表2的定量比较也给出自适应CKFSTF关于位置的滤波精度是高于CKFSTF，可见自适应CKFSTF能有效的减小因噪声统计特性不准确而产生的估计误差，有效的提高了滤波精度。另外，在仿真研究中发现不准确的噪声统计特性还容易导致CKFSTF发散，如图8所示，而带噪声估值器的自适应CKFSTF能有效的克服发散现象。由此也验证了在系统过程噪声统计特性未知或不准确的情况下，自适应CKFSTF仍能准确的对状态进行跟踪，具有更强的应对过程噪声统计特性变化的自适应能力。

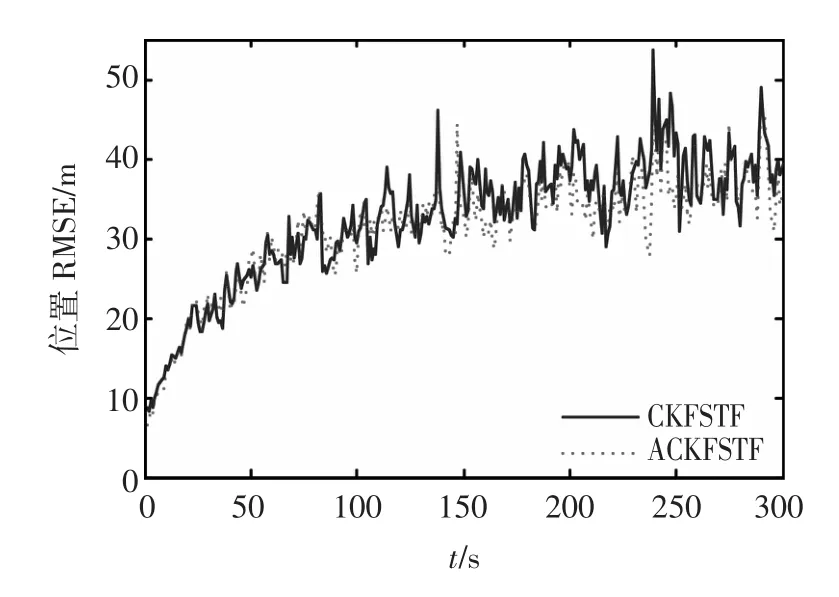
图5 两种算法下位置的均方根误差Fig.5 RMSEsofpositionintwoalgorithms

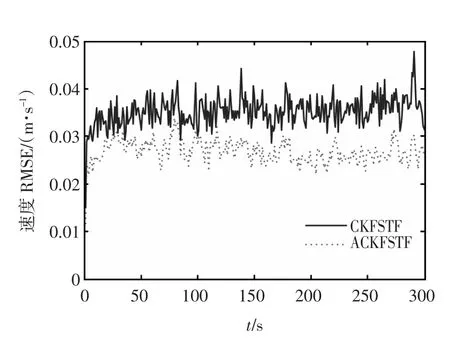
图6 两种算法下速度的均方根误差Fig.6 RMSEsofvelocityintwoalgorithms

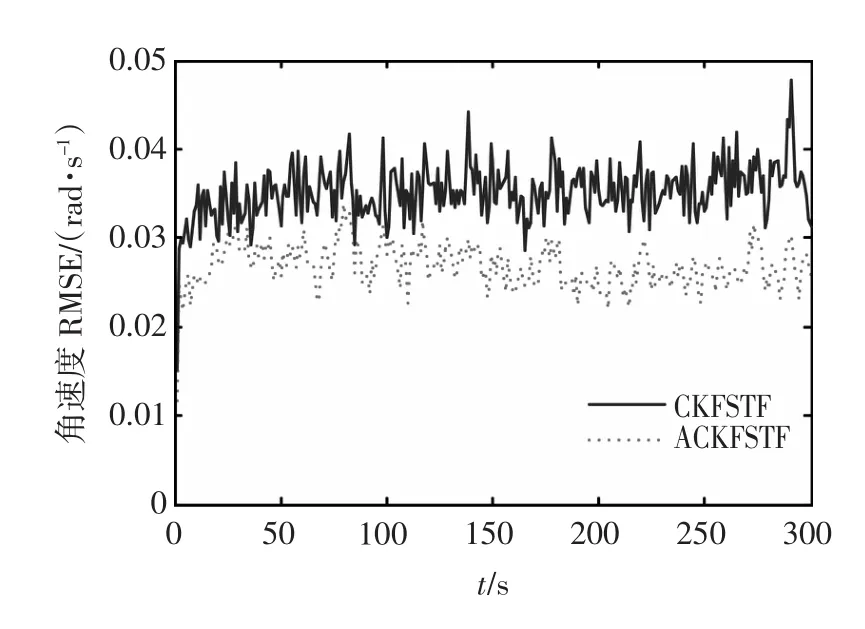
图7 两种算法下角速度的均方根误差Fig.7 RMSEsofangularvelocityintwoalgorithms

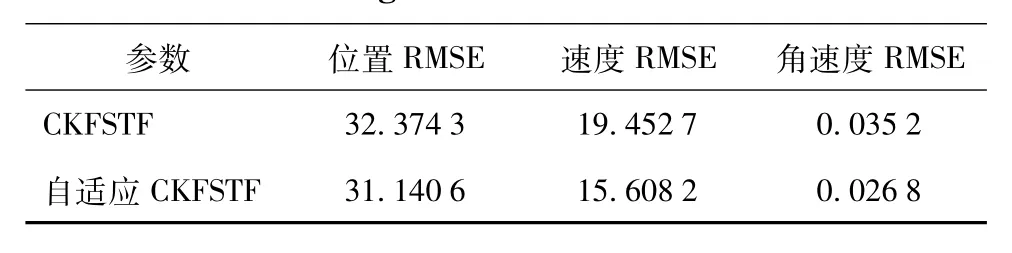
表2 两种算法下状态估计RMSEs的均值Table2 AverageRMSEsofstateestimationin twoalgorithms

4 结论

针对STF需求取雅可比矩阵并要求非线性系统的状态函数和量测函数连续可微等理论局限以及基于UT变换的强跟踪算法处理高维非线性滤波问题滤波精度不佳甚至发散等问题，本文将强跟踪滤波器与容积卡尔曼滤波器结合，提出了CKFSTF算法。理论分析与仿真结果表明，对于模型不确定的强非线性系统，CKFSTF能实现系统参数和状态的快速准确跟踪，有效的克服了STF的理论局限。相比于UT变换的强跟踪器，CKFSTF能对高维（n≥3）非线性系统的状态进行准确估计，且有效缩短了计算时间。此外，对于过程噪声统计特性未知的目标跟踪问题，将CKFSTF进行了相应的改进，增加了Sage-Husa噪声统计估值器，得到了自适应CKFSTF算法，它能增强滤波器关于噪声统计特性变化的自适应能力，有效地提高状态估计精确度。

∶

［1］周东华，叶银忠.现代故障诊断与容错控制［M］.北京∶清华大学出版社，2000∶60-68.

［2］SPETHM，DAECKED，MEYRH.MinimumoverheadburstsynchronizationforOFDMbasedbroadbandtransmission［C］//Global TelecommunicationsConference，November8，1998，Sydney，NSW.1998，5∶2777-2782.

［3］周聪，肖建.基于自适应强跟踪滤波器的汽车行驶状态软测量［J］.电机与控制学报，2012，16（2）∶96-101. ZHOUCong，XIAOJian.Softcomputingforvehiclestateestimationbasedonadaptivestrongtrackfilter［J］.ElectricMachines andControl，2012，16（2）∶96-101.

［4］王小旭，赵琳，夏全喜，等.基于Unscented变换的强跟踪滤波器［J］.控制与决策，2010，25（7）∶1063-1068. WANGXiaoxu，ZHAOLin，XIAQuanxi，etal.Strongtracking filterbasedonunscentedtransformation［J］.ControlandDecision，2010，25（7）∶1063-1068.

［5］王小旭，赵琳，薛红香.强跟踪CDKF及其在组合导航中的应用［J］.控制与决策，2010，25（12）∶1837-1842. WANGXiaoxu，ZHAOLin，XUEHongxiang.StrongtrackingCDKFandapplicationforintegratednavigation［J］.ControlandDecision，2010，25（12）∶1837-1842.

［6］ARASARATNAMI，HAYKINS.CubatureKalmanfilters［J］. IEEETransactionsonAutomaticControl，2009，54（6）∶1254-1269.

［7］王小旭，潘泉，黄鹤，等.非线性系统确定采样型滤波算法综述［J］.控制与决策，2012，6（27）∶801-812. WANGXiaoxu，PANQuan，HUANGHe，etal.Overviewofdeterministicsamplingfilteringalgorithmsfornonlinearsystem［J］. ControlandDecision，2012，6（27）∶801-812.

［8］孙枫，唐李军.Cubature卡尔曼滤波和Unscented卡尔曼滤波估计精度比较［J］.控制与决策，2013，28（2）∶303-308. SUNFeng，TANGLijun.Estimationprecisioncomparisonofcubaturekalmanfilterandunscentedkalmanfilter［J］.Controland Decision，2013，28（2）∶303-308.

［9］GUSTAFSSONF，HENDEBYG.SomerelationsbetweenextendedandunscentedKalmanfilters［J］.IEEETransactionsonSignal Processing，2012，60（2）∶545-555.

［10］LIUJ，CAIBG，TANGT，etal.ACKFbasedGNSS/INStrain integratedpositioningmethod［C］//2010InternationalConferenceonMechatronicsandAutomation（ICMA），August4-7，2010，Xi’an，China.2010∶1686-1689.

［11］徐树生，林孝工.基于鲁棒CKF的多传感器全信息融合算法［J］.电机与控制学报，2013，17（2）∶90-111. XUShusheng，LINXiaogong.Multi-sensorallinformationfusionalgorithmbasedonrobustCKF［J］.ElectricMachinesand Control，2013，17（2）∶90-111.

［12］石勇，韩崇昭.自适应UKF算法在目标跟踪中的应用［J］.自动化学报，2011，37（6）∶755-759. SHIYong，HANChongzhao.AdaptiveUKFmethodwithapplicationstotargettracking［J］.ActaAutomaticaSinica，2011，37（6）∶755-759.

［13］WANGZS，HUY，WANGDB，etal.Multi-sensorattitude determinationsystembasedonstrongtrackingfilter［J］.Journal ofNanjingUniversityofAeronautics＆Astronautics，2009，41（1）∶64-68.

［14］LEEDJ.Nonlinearestimationandmultiplesensorfusionusing unscentedinformationfiltering［J］.IEEESignalProcessing Lett.，2008，15∶861-864.

［15］邓自立，王建国.非线性系统的自适应推广的Kalman滤波［J］.自动化学报，1987，13（5）∶375-379. DENGZili，WANGJianguo.AdaptiveextendKalmanfilterfor nonlinearsystem［J］.ActaAutomaticaSinica，1987，13（5）∶375-379.

［16］张汉国，张洪钺.阻止自适应Kalman滤波发散的补救方法［J］.控制与决策，1991，6（1）∶53-56. ZHANGHanguo，ZHANGHongyue.RescuemethodforpreventingthedivergenceofadaptiveKalmanfiltering［J］.Controland Decision，1991，6（1）∶53-56.

（编辑∶刘琳琳）

AdaptiveCKFstrongtrackingfilterandapplication

DINGJia-lin1，XIAOJian1，ZHAOTao2
（1.SchoolofElectricalEngineering，SouthwestJiaotongUniversity，Chengdu610031，China；2.SchoolofTransportationandLogistics，SouthwestJiaotongUniversity，Chengdu610031，China）

∶FortheproblemthatStrongtrackingfilter（STF）hassometheoreticallimitationsandtheSTF basedonunscentedtransformation（UTSTF）declinesinaccuracyandfurtherdivergeswhensolvingthe nonlinearfilteringprobleminhighdimension，acubatureKalmanfilter（CKF）withstrongtrackingbehavior（CKFSTF）wasproposed.CKFSTFcombinesadvantagesofSTFandCKF∶strongrobustness，highaccuracy，strongnumericalstability，fastcalculationspeed，easyimplementationandwiderangeof applications.Furthermore，adaptiveCKFSTFwasproposedwhenthepriornoisestatisticisunknownand time-varying，whichusingSage-HusanoisestatisticestimatorbasedonCKFSTF.Validityofthenewproposedalgorithmwasverifiedbythesimulationexamples.

∶strongtrackingfilter；cubaturekalmanfilter；adaptability；targettracking

∶TP273

∶A

∶1007-449X（2015）11-0111-10

∶2013-10-06

∶国家自然科学基金（51177137）；国家自然科学基金重点项目（61134001）

∶丁家琳（1986—），女，博士研究生，研究方向为非线性滤波算法及其在电机状态估计中应用；肖 建（1950—），男，教授，博士生导师，研究方向为交流传动系统，模糊控制和计算机控制；赵 涛（1988—），男，博士研究生，研究方向为二型模糊系统、智能控制。

∶丁家琳

DOI∶10.15938/j.emc.2015.11.017