矩阵式整流器的输入滤波器谐振抑制算法

刘晓，张庆范，侯典立（.国网技术学院，山东济南 5000；.山东大学控制科学与工程学院，山东济南 5006；.鲁东大学信息与电气工程学院，山东烟台 6405）

矩阵式整流器的输入滤波器谐振抑制算法

刘晓1，张庆范2，侯典立3
（1.国网技术学院，山东济南 250002；2.山东大学控制科学与工程学院，山东济南 250061；3.鲁东大学信息与电气工程学院，山东烟台 264025）

∶结合单周期控制策略和主动阻尼算法，提出了一种适用于矩阵整流器的简单易行的输入滤波器谐振抑制方法。通过参数估计计算阻尼电流，减少了算法所需传感器数量。在考虑实际控制器所造成延时的基础上，建立了包括主动阻尼算法和输入滤波器在内的数学模型，利用零极点图分析其稳定性，为虚拟电阻参数整定提供了理论依据。利用单周期控制策略简化了软件复杂程度，使主动阻尼算法更易于工程实现。实验结果证明，引入本文所提算法后，矩阵整流器网侧输入电流中谐振点附近的谐振峰值从10％以上下降至2.5％以下，输入电流的总谐波畸变率（TotalHarmonicDistortion，THD）从18.75％下降至5.23％，试验结果验证了理论分析的正确性和控制策略的可行性。

∶矩阵整流器；主动阻尼；单周期控制；谐振抑制

0 引言

三相交流-直流矩阵式变换器（以下简称矩阵式整流器）是一种由三相交流-交流矩阵式变换器发展而来的新型“绿色”通用整流装置。由于其具有正弦输人电流、能量可双向流动、输人功率因数任意可控、体积小、重量轻等优点［1］，受到众多学者的广泛关注［2-4］。

在实际应用中，通常在电网和开关矩阵之间串联LC输人滤波器，以滤除输人电流中由于功率电路开关动作而产生的高次谐波分量，减少对电网的谐波污染；同时改善输人电压的波形畸变，以免其影响输出电能质量。但是，LC输人滤波器也会带来很多问题，甚至使系统无法正常工作［5-7］。根本原因是LC网络具有谐振特性，可能会被电网中潜在的谐波分量（串联谐振，seriesresonance）或者被矩阵式整流器自身激发（并联谐振，parallelresonance），导致输人电流的严重畸变。为了抑制输人滤波器谐振，通常的做法是在滤波电感上并联阻尼电阻［8-9］，降低谐振峰值使系统稳定。这种技术被称为“被动阻尼”（PassiveDamping），具有结构简单可靠，无需算法支持等优点，在工业中得到了广泛应用。但物理阻尼电阻的引人会增加损耗，降低系统效率，尤其是在大功率的情况下，阻尼电阻发热明显，能量消耗严重。

为了在不改变变换器结构、不影响效率的前提下，改善系统稳定性和输人电流质量，文献［10］提出了一种应用“主动阻尼”（ActiveDamping）技术的新型控制方法，该算法检测滤波电容电压，经过一阶数字低通滤波器之后用于占空比计算，可以得到与带有阻尼电阻的LC滤波器-矩阵变换器系统近似的动态性能和稳定性，但系统中需要额外增加三个电压传感器。

文献［11-14］中提出了多种应用于三相电流源型PWM整流器的“主动阻尼”算法，这些控制策略的基本思路是在滤波电容上并联一个“虚拟”的阻尼电阻，并使由于谐振产生的谐波电流流过这个电阻。由于三相电流源型PWM整流器使用的调制策略与矩阵式整流器常用的空间矢量调制策略（SpaceVectorModulation，SVM）类似，因此这些算法同样可用于矩阵式整流器系统。该种算法首先对阻尼电流进行归一化（Normalization）处理，加人至指令输人电流矢量之中后，重新计算调制度和矢量相角，并判断指令输人电流矢量所处扇区，最后计算占空比。使用这种调制策略时，运算量较大，编程困难。同时，此类算法也需要额外的传感器检测滤波电容电压。

文献［15］借鉴上述思路，介绍了一种利用电流预测控制技术（PredictiveCurrentControl，PCC）在三相交流-交流矩阵式变换器的输出侧合成阻尼电流的新方法。PCC控制技术具有快速动态响应、算法易于理解、灵活性高等优点，但是文中所介绍方法的运算量更大，需要高性能DSP或者FPGA芯片执行算法。

本文提出了一种新型的低成本“主动阻尼”算法。该算法检测网侧电流，通过参数估计取得开关矩阵输人电压信号，计算流过虚拟电阻的谐波电流后，利用单周期控制策略［16-17］（One-CycleControl，OCC）在网侧输人电流中将其合成出来。由于无需计算调制度和输人电流矢量相角，软件复杂度得到了极大的简化，易于工程实现；另外，网侧电流传感器同样用于对系统提供过电流保护，一般是必需的，因此本算法未增加系统成本。文中分析了系统稳定性和“虚拟电阻”参数整定方法，最后给出实验结果验证了本算法的可行性和有效性。

1 矩阵式整流器的“主动阻尼”算法

1.1 基于电容电压的“主动阻尼”算法

如图1所示，为矩阵式整流器系统结构图。若不考虑“主动阻尼”算法，即系统中不含虚拟阻尼Rd时，输人滤波器的电压、电流方程为∶

三相电源 输入滤波器 开关矩阵 输出电抗器 负载

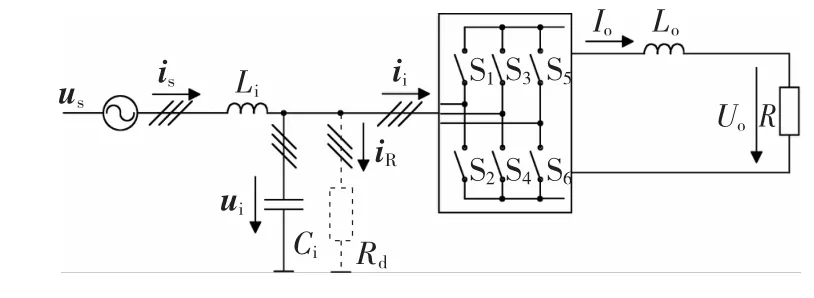
图1 矩阵式整流器系统结构图Fig.1 Systemschemeofmatrixrectifier

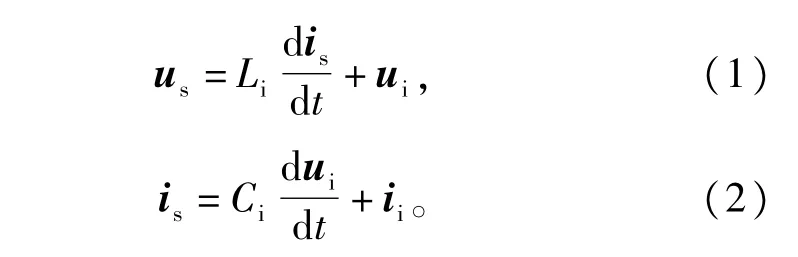
式中∶Li和Ci分别为输人滤波电感、电容；us=［uaubuc］T和is=［iaibic］T分别为网侧输人电压、电流矢量；ui=［uiauibuic］T和ii=［iiaiibiic］T分别为开关矩阵输人电压、电流矢量。以us和ii为输人变量，以ui和is为输出变量，可得拉氏域下的输出表达式为∶

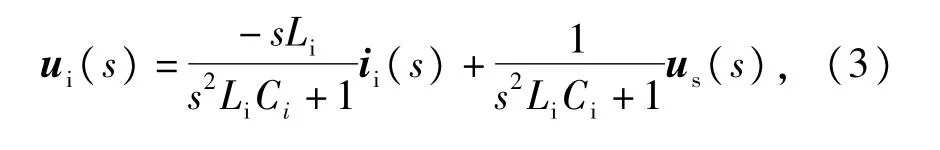
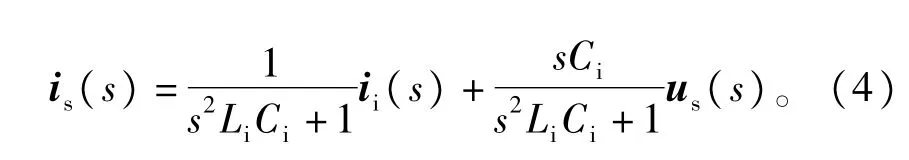
由式（3）和式（4）可见，输人滤波器存在一个固有的谐振频率，并且会被电网中潜在的谐波分量激发（串联谐振）；或者被开关矩阵输人电流ii中的谐波激发（并联谐振），引起网侧输人电流is和电容电压ui的剧烈震荡，导致系统不稳定。

“主动阻尼”技术通过在滤波电容旁路并联虚拟阻尼Rd，可以在不影响变换器效率的前提下，衰减输人滤波器谐振产生的谐波分量，同时不影响基波分量［11-14］。如图1所示，引人Rd后，输人滤波器电流方程式（2）应变为∶

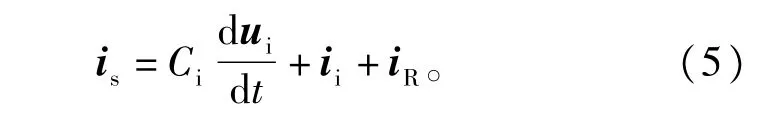
虚拟阻尼中流过的电流iR与电容电压ui成比例关系∶

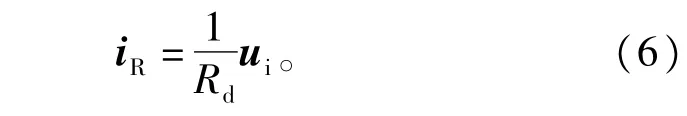
由于“主动阻尼”衰减的是输人滤波器中的谐波分量而不是基波分量，因此计算阻尼电流iR时，应使用电容电压ui中的谐波成分uih。为了实现这一目的，首先遵循幅值不变的原则，将ui变换至与网侧输人电压同步旋转的d-q坐标系下∶

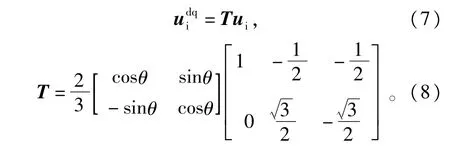
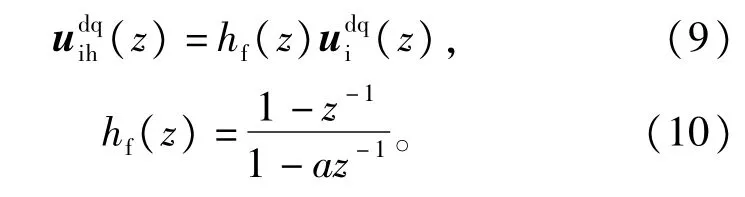
式（10）为数字直流阻断器的z域传函，a为其参数［18］，本文中取a=0.995。采样周期为Ts，对上式进行双边拉氏变换，可得数字直流阻断器的拉氏域传函为∶

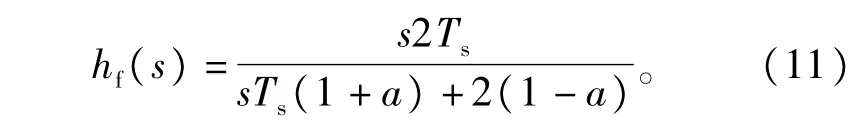
式（9）可变为∶

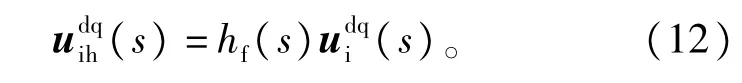
综上所述，可得基于电容电压的“主动阻尼”算法框图如图2所示。

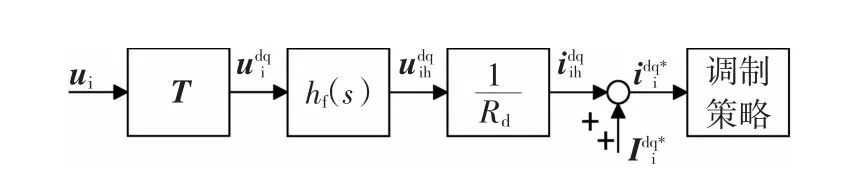
图2 基于电容电压的“主动阻尼”算法框图Fig.2 Blockdiagramofcapacitorvoltagebased “ActiveDamping”strategy

1.2 基于网侧输入电流的“主动阻尼”算法

基于电容电压的“主动阻尼”算法思路清晰、运算量小。但需要额外增加三个电压传感器检测电容电压，增加了系统成本和硬件设计难度。在矩阵式整流器系统中，输人侧必须配置的传感器是网侧电压传感器和网侧电流传感器，前者用于软件锁相环（PhaseLockLoop，PLL）、执行换流策略和提供输人电源过压、欠压保护，后者用于提供输人电流过流保护。

本文将传感器检测得到的us和is带人式（1），对电容电压ui进行参数估计∶

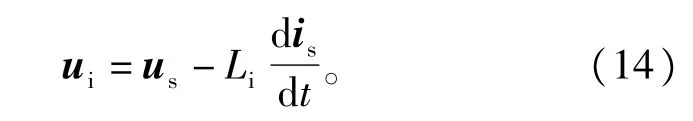
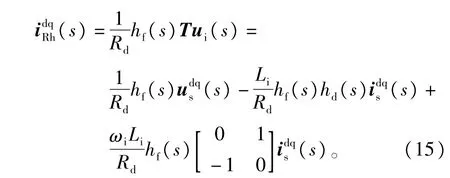
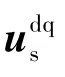
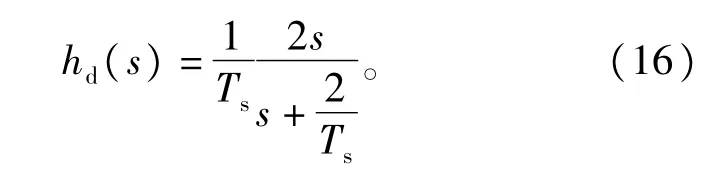
对式（15）进行深人分析，可见∶在基于网侧输人电流的“主动阻尼”算法中，阻尼电流是三个部分线性组合得到的。

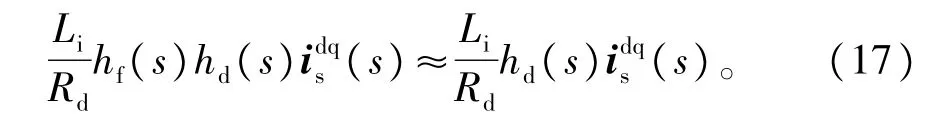
综上所述，基于网侧输人电流的“主动阻尼”算法框图如图3所示。

图3 基于网侧输入电流的“主动阻尼”算法框图Fig.3 Blockdiagramofgrid-sideinputcurrentbased “ActiveDamping”strategy

1.3 基于网侧输入电流的“主动阻尼”算法稳定性分析

上述基于网侧输人电流的“主动阻尼”算法省去了电容电压传感器，节约了系统成本，同时运算量更小，降低了编程难度。

在实际应用中，由于控制器进行模拟-数字采样、坐标变换、信号滤波等运算需要时间，这种延时会造成相角裕度的减小，使系统的控制性能恶化。因此，使用理想控制器对系统的稳定性进行分析是不可靠的。本文所使用数字信号处理器（Digital SignalProcessor，DSP）存在约1个开关周期的延时，其中一半的时间用于模拟-数字采样，一半的时间用于计算阻尼电流和执行调制策略。

考虑实际控制器延时，并引人输人滤波器传递函数，可得基于网侧输人电流的“主动阻尼”算法闭环控制系统模型如图4所示。

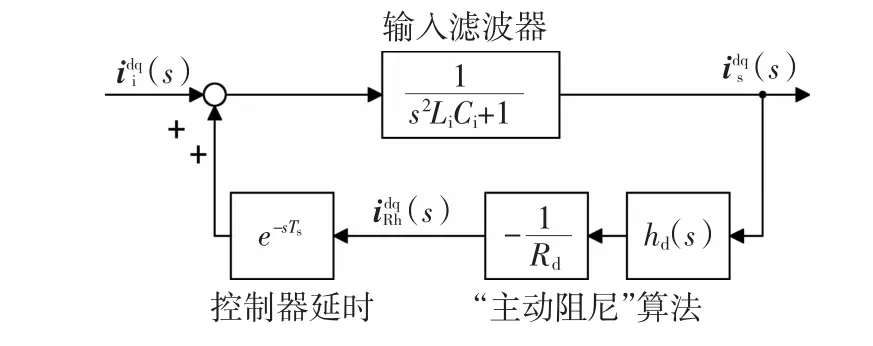
图4 基于网侧输入电流的“主动阻尼”算法控制系统模型Fig.4 Modelofgrid-sideinputcurrentbased “ActiveDamping”controlsystem

当Rd取不同值时，利用Matlab软件绘制上述闭环控制系统的Bode图和零极点轨迹如图5所示。

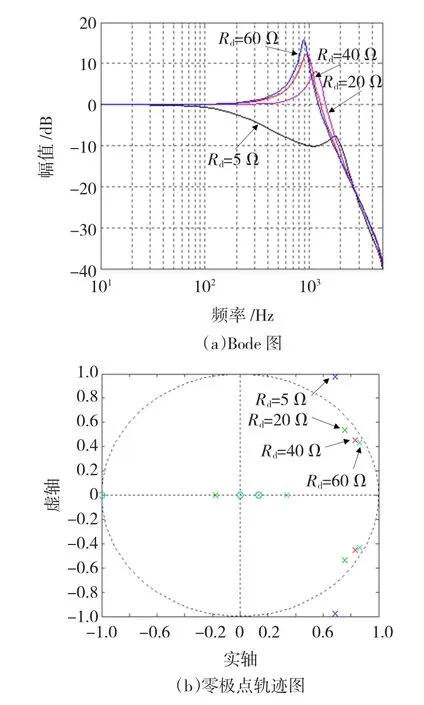
图5 Rd取不同值时的算法稳定性分析Fig.5 StabilityanalyzewithdifferentRdvalues

由图5（a）可见，Rd越小，“主动阻尼”算法对谐振峰值的拟制效果越明显。但是，由图5（b）可见，Rd减小时，系统位于z平面右侧的一对共扼极点将向单位圆外移动，影响系统稳定性。以本文所选择滤波器参数（Li=3mH，Ci=13μF，谐振频率ωres= 805Hz）为例，使系统临界稳定的Rd最小值Rd-min约为12Ω。

2 矩阵式整流器的单周期控制策略

本文选择使用单周期控制策略（One-CycleControl，OCC）在矩阵式整流器的输人侧合成阻尼电流。OCC控制技术是一种新颖的非线性控制技术，能够逐周期的调节开关器件的占空比，在一个开关周期内实现控制目标，而且OCC控制还具有鲁棒性好、瞬时响应速度快、抗干扰能力强等优点。本文选择OCC控制技术的主要原因在于这种调制策略以开关矩阵输人电流为控制对象，引人“主动阻尼”算法后，仅需调整开关矩阵输人电流的期望值即可，非常易于工程实现。

文献［16］中对单周期控制矩阵式整流器的系统模型、控制思路、实现方法等进行了详细的阐述。但是文中直接利用输人相电流的峰值参考量计算输人电流的参考信号，并强迫输人电流矢量与输人电压矢量同相位，未实现对输人电流中有功分量和无功分量的解耦控制，算法不够灵活。本文针对“主动阻尼”算法要求对输人电流中d轴和q轴分量单独控制的特点，以文献［16］为基础，对积分器指令值的生成方法和电流扇区号N的判断方法进行了改进，如图6中虚线框所示。

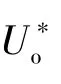
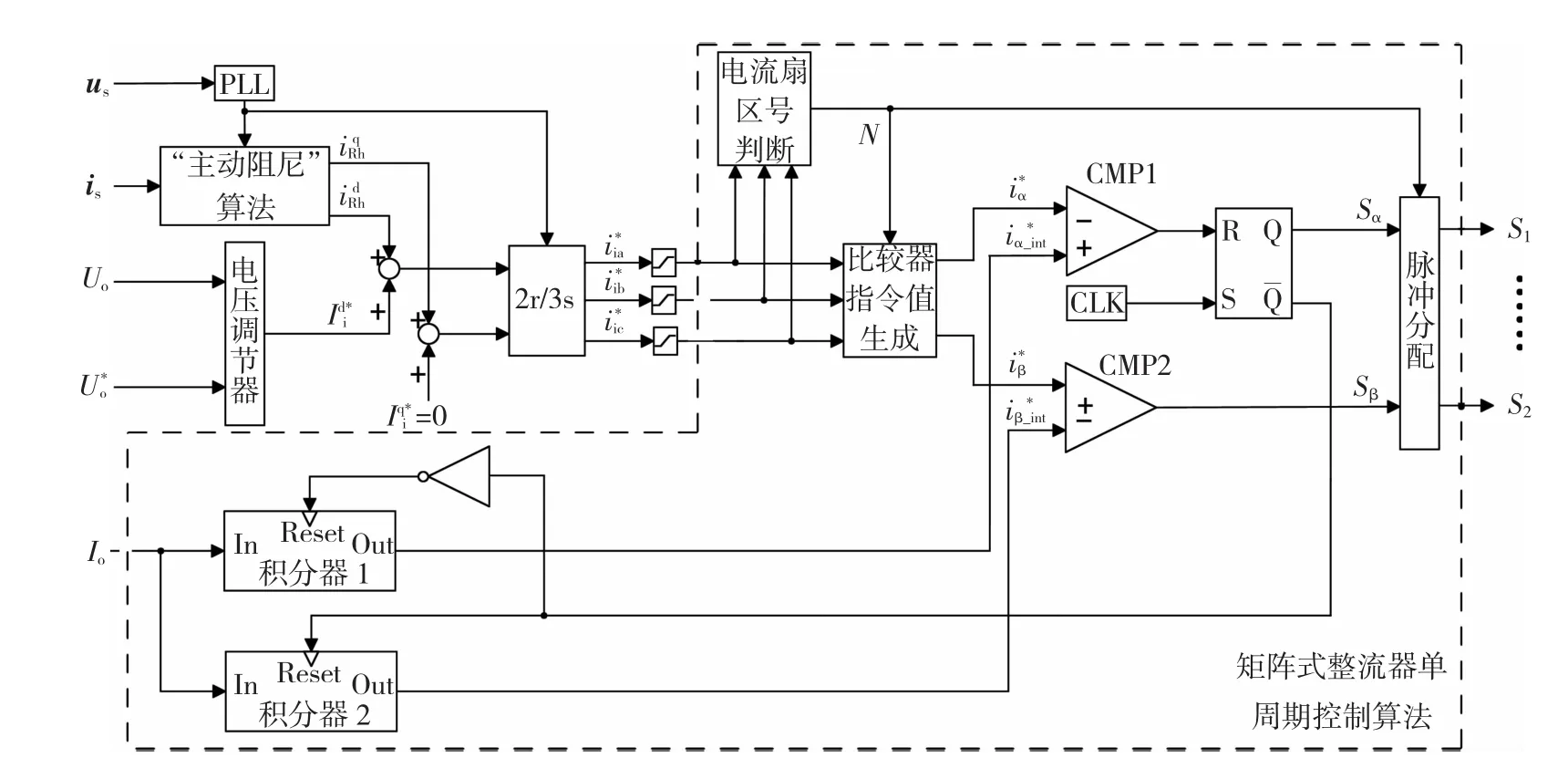
图6 矩阵式整流器“主动阻尼”-单周期控制策略框图Fig.6 BlockdiagramofOCCwith“ActiveDamping”strategyformatrixrectifier

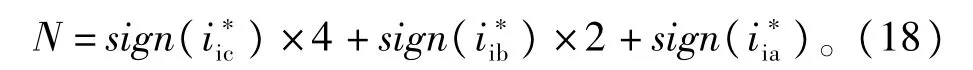
上式中，sign（）表示取符号运算∶

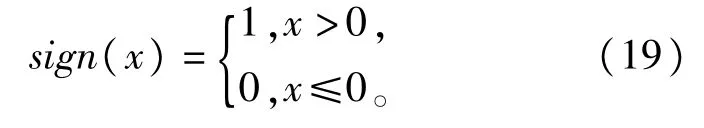
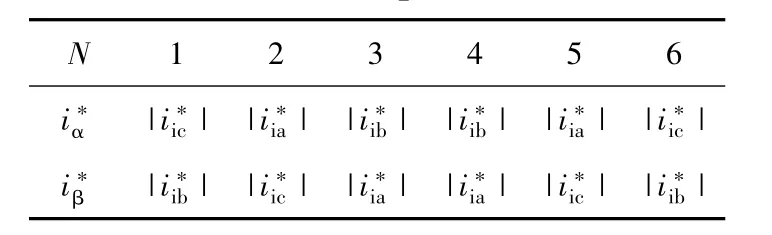
表1 扇区号与比较器指令值的对应关系Table1 Relationshipbetweenthesectorsofinput currentandcomparereferences

在每个开关周期内，单周期控制器对驱动信号Sα、β的控制规律；不同输人电流扇区内，Sα、β与6个双向开关的对应关系；单周期控制器的建模、仿真、实现方式等可参见文献［16］，本文不再重复。

本文通过对单周期控制策略的改进，实现了输人有功电流和无功电流的解耦控制，算法简单，易于应用。引人“主动阻尼”算法后，无需计算调制度、输人电流相角等变量，软件复杂程度得到了极大的简化。

3 虚拟电阻的参数整定

阻尼电流idqRh中仅含交流分量，不含直流分量，平均值为0，因此正常情况下，“主动阻尼”算法的引人不会对输出直流电压Uo和输人无功功率产生影响。

4 实验研究

4.1 实验装置

为了验证上述理论分析的正确性，搭建了由强电电路和弱电电路组成的矩阵式整流器实验装置（如图7所示），强电电路主要包括输人滤波器、双向功率开关矩阵、输出平波电抗器、阻性负载等，弱电电路包括DSP（TITMS320F2812）和CPLD（Xilinx XC9572XL）组成的控制系统，网侧电压、电流检测电路，输出电压、电流检测电路，以及驱动电路等。实验参数∶三相输人电压每相60V/50Hz；开关频率12kHz；输人滤波电感电容3mH/13μF，谐振频率ωres=805Hz；输出平波电抗器5mH；负载电阻25Ω；虚拟阻尼Rd=25Ω。

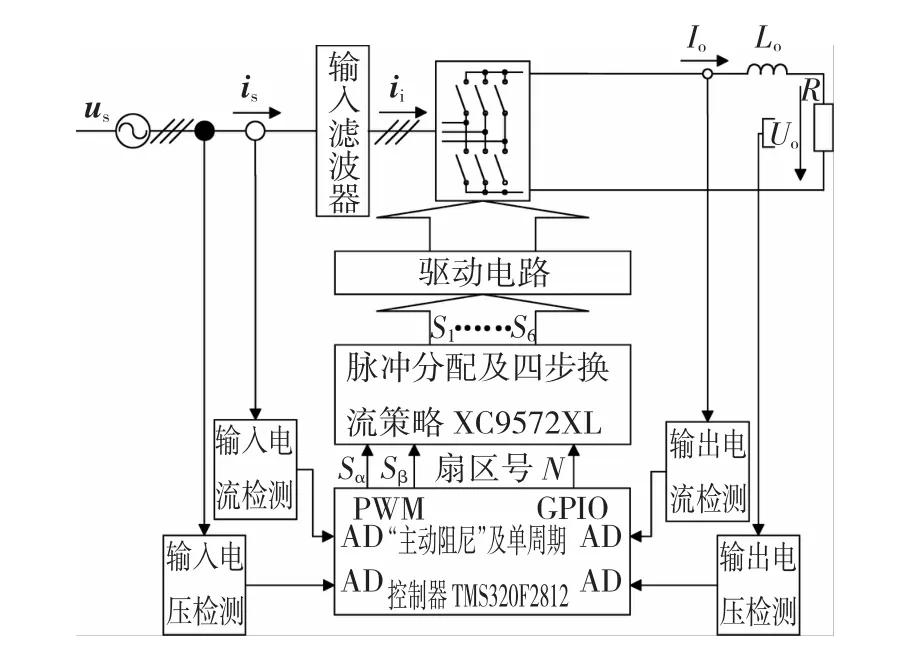
图7 实验装置Fig.7 Experimentalconfiguration

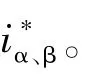
表2 扇区号与双向开关驱动信号的对应关系Table2 Relationshipbetweenthesectorsofinputcurrent andbi-directionalswitchdrivesignal

表2中，“1”表示开通，“0”表示关断，S0为零矢量的作用时间，用于为负载提供续流通路，当Sα、Sβ均为低电平时，S0为高电平。

4.2 “主动阻尼”-单周期控制策略静态特性实验

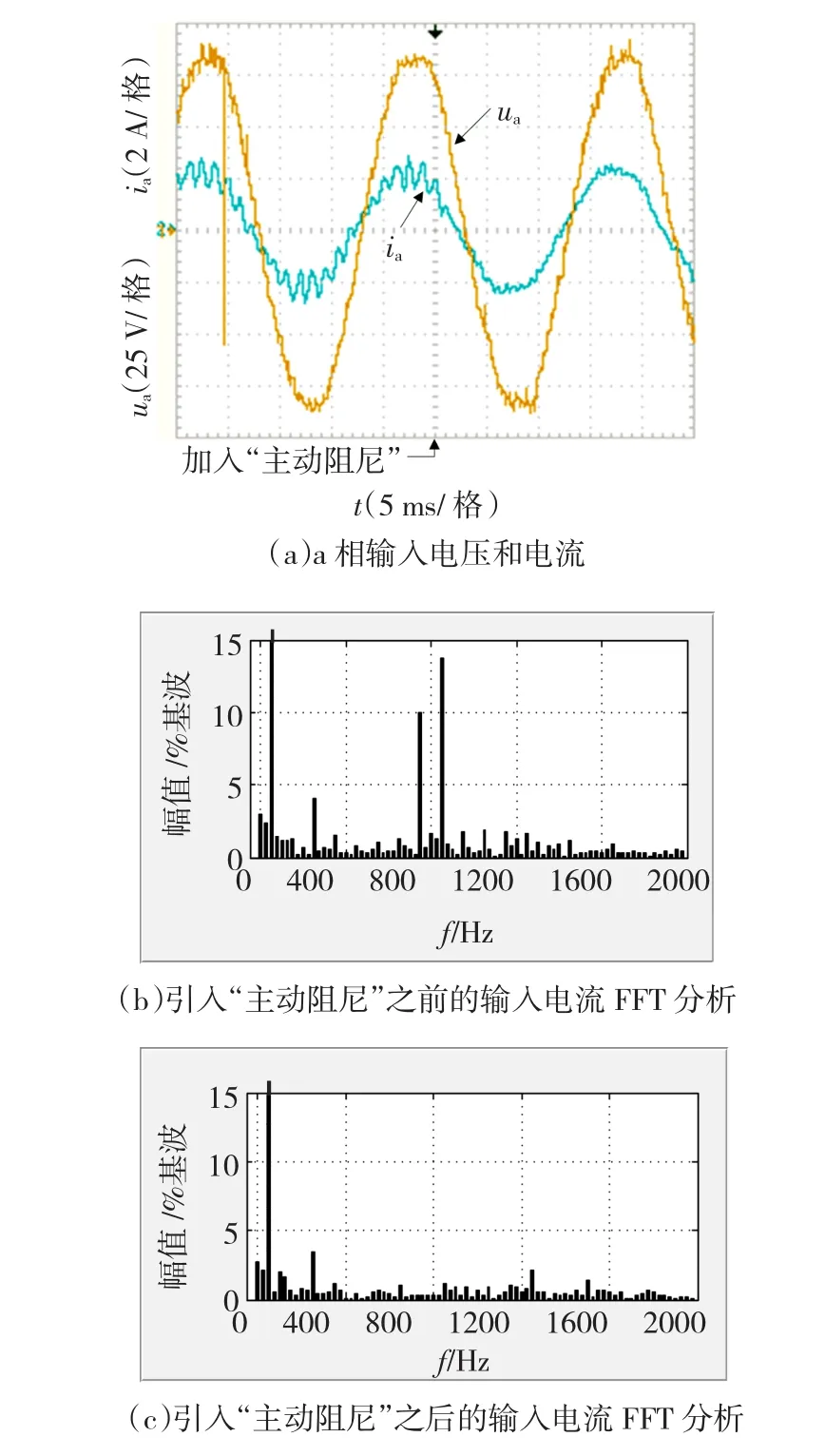
图8 网侧输入电流实验结果及其FFT分析Fig.8 Experimentalwaveformsofthegrid-side inputcurrentandtheirFFT

通过图8可见，未加人“主动阻尼”算法时，输人电流在谐振点805Hz附近发生了震荡，15次和17次谐波的幅值分别为基波幅值的10％和14％，输人电流的总谐波畸变率（TotalHarmonicDistortion，THD）为18.75％；引人“主动阻尼”算法之后，输人电流稳定，谐振频率附近的谐波幅值被衰减，降至基波幅值的2.5％以下，输人电流的THD降至5.23％，输人电流的波形质量得到了改善。需要指出的是，图8（a）中输人电压与电流的相位差是输人滤波电容造成的，“主动阻尼”算法对50Hz基波幅值和相位都没有明显影响。

4.2 “主动阻尼”-单周期控制策略动态特性实验

图9和图10分别为指令输出电压U*o由50V突变为100V和负载由15Ω突变为25Ω时（U*o= 80V）的实验结果。

由图9可见，指令输出电压突变时，直流输出和输人电流在一个电源周期（20ms）内即达到新的稳态值，调节过程中无超调，动态响应速度可以接受。调节前后，直流输出电压均可以准确跟踪指令值，无静态误差。

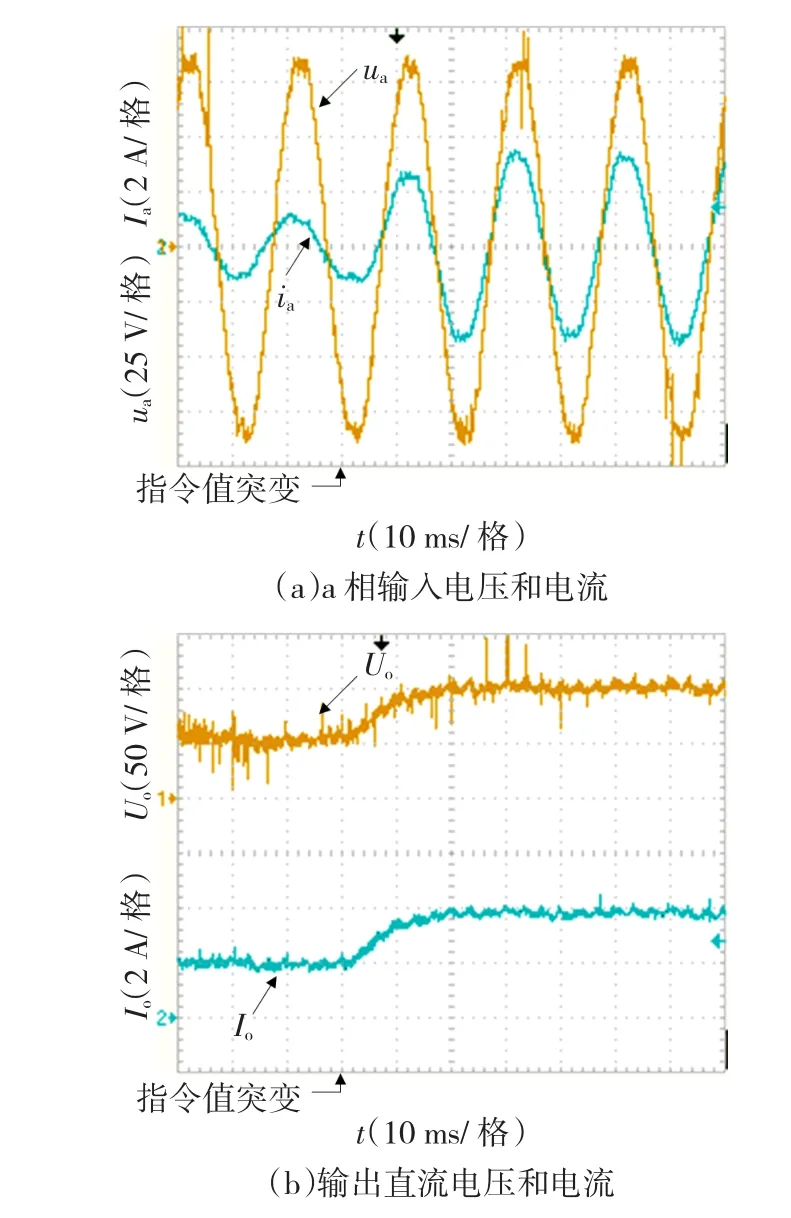
图9 指令输出电压由50V突变为100V实验结果Fig.9 Experimentalresultswhenoutputvoltagereference stepchangesfrom50Vto100V

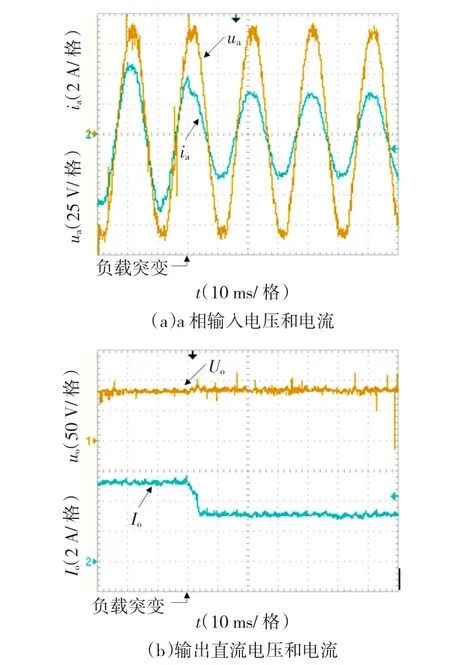
图10 负载由15Ω突变为25Ω实验结果Fig.10 Experimentalresultswhenloadresistorstep changesfrom15Ωto25Ω

由图10可见，当负载发生突变时，输人电流和输出电流能够在6ms左右进人稳定状态，同时，负载突变对输出直流电压没有明显影响。

无论在指令值突变还是在负载突变情况下，输人电流均保持稳定、无谐振，过渡过程平滑。说明“主动阻尼”算法在系统动态变化的过程中也可以很好的抑制输人滤波器谐振，提高了系统动态稳定性。

5 结论

本文通过对“主动阻尼”-单周期控制策略进行理论分析和实验研究，可得到以下结论∶

1）本算法利用虚拟电阻代替实际电阻，衰减输人滤波器造成的电流谐振，在不增加系统功耗的前提下，改善网侧输人电流波形和系统稳定性，取得了良好的实验结果。

2）本算法利用参数估计计算阻尼电流，减少了所需传感器数量，有助于降低整机成本和硬件设计要求。文中给出了虚拟阻尼参数整定方法并进行了理论分析，对本算法的局限性进行了讨论。

3）通过对矩阵式整流器单周期控制策略进行改进，实现了对网侧输人有功和无功电流的解耦控制，并利用其在网侧输人电流中合成阻尼电流，简化了软件复杂程度，提高了稳态控制精度和动态响应速度，更利于工程实现。

∶

［1］文锋，姜久春，郭慧萍.基于矩阵变换器的AC-DC变换器［J］.电工技术学报，2009，24（3）∶129-131. WENFeng，JIANGJiuchun，GUOHuiping.AC-DCconverter basedonmatrixconverter［J］.TransactionsofChinaElectrotechnicalSociety，2009，24（3）∶129-131.

［2］HOLMES，DG，LIPOTA.ImplementationofacontrolledrectifierusingAC-ACmatrixconvertertheory［J］.IEEETransactions onPowerElectronics，1992，7（1）∶240-249.

［3］徐壮，殷冠贤，徐殿国.车用新型AC-DC矩阵式变换器［J］.电工技术学报，2011，26（8）∶64-70. XUZhuang，YINGuanxian，XUDianguo.Anewbidirectional AC-DCconverterusingamatrixconvertertopology［J］.TransactionsofChinaElectrotechnicalSociety，2011，26（8）∶64-70.

［4］许烈，张奇，李永东，等.混合电动汽车功率变换器的研究［J］.电机与控制学报，2014，18（1）∶98-104. XULie，ZHANGQi，LIYongdong，etal.ResearchontheHEV basedpowerconverter［J］.ElectricMachinesandControl，2014，18（1）∶98-104.

［5］CASADEID，CLAREL，EMPRINGHAML，etal.Large-siganl modelforthestabilityanalysisofmatrixconverter［J］.IEEE TransactionsonIndustrialElectronics，2007，54（2）∶939-950.

［6］CASADEID，SERRAG，TANIA，etal.Theoreticalandexperimentalinvestigationonthestabilityofmatrixconverters［J］. IEEETransactionsonIndustrialElectronics，2007，52（5）∶1409 -1419.

［7］粟梅，覃恒思，孙尧，等.矩阵变换器系统的稳定性分析［J］.中国电机工程学报，2005，25（8）∶62-69. SUMei，QINHengsi，SUNYao，etal.Stabilityanalysisofmatrix converterdrivesystem［J］.ProceedingsoftheCSEE，2005，25（8）∶62-69.

［8］佘宏武，林桦，王兴伟，等.矩阵变换器的阻尼输人滤波器设计［J］.电源学报，2011，33（1）∶19-25. SHEHongwu，LINHua，WANGXingwei，etal.Dampedinput filterdesignofmatrixconverter［J］.JournalofPowerSupply，2011，33（1）∶19-25.

［9］粟梅，孙尧，覃恒思，等.矩阵变换器输人滤波器的多目标优化设计［J］.中国电机工程学报，2007，27（1）∶70-75. SUMei，SUNYao，QINHengsi，etal.Anmulti-objectiveoptimizeddesignofinputfilterofmatrixconverter［J］.Proceedingsof theCSEE，2007，27（1）∶70-75.

［10］粟梅，孙尧，覃恒思，等.一种改善矩阵变换器系统动态性能和稳定性的控制方法［J］.电工技术学报，2005，20（12）∶18-23. SUMei，SUNYao，QINHengsi，etal.Effectoftheinputfilter onstabilityofmatrixconverterdrivesystem［J］.Transactionsof ChinaElectrotechnicalSociety，2005，20（12）∶18-23.

［11］WISEMANJC，WUBin.Activedampingcontrolofahigh-powercurrent-sourcerectifierforline-currentTHDreduction［J］. IEEETransactionsonIndustrialElectronics，2005，52（3）∶758 -764.

［12］LIYW.Controlandresonancedampingofvoltage-sourceand current-sourceconverterswithLCfilters［J］.IEEETransactions onIndustrialElectronics，2009，56（5）∶1511-1521.

［13］LIYunwei，WUBin，ZARGARINR，etal.DampingofPWM current-sourcerectifierusingahybridcombinationapproach［J］. IEEETransactionsonPowerElectronics，2007，22（4）∶1383-1393.

［14］QIUAM，LIYunwei，WUBin，etal.Highperformancecurrent sourceinverterfedinductionmotordrivewithminimalharmonic distortion［C］//IEEEPowerElectronicsSpecialistsConference，2007∶79-85.

［15］RIVERAM，ROJASC，RODRIGUEZJ，etal.Predictivecurrentcontrolwithinputfilterresonancemitigationforadirectmatrixconverter［J］.IEEETransactionsonPowerElectronics，2011，26（10）∶2794-2803.

［16］杨兴华，杨喜军，张哲民，等.矩阵整流器单周期控制策略的研究［J］.电工技术学报，2012，27（2）∶38-44. YANGXinghua，YANGXijun，ZHANGZhemin，etal，Research onone-cyclecontrolstrategyofmatrixrectifier［J］.Transactions ofChinaElectrotechnicalSociety，2012，27（2）∶38-44.

［17］SMEDLEYKM，CUKS.Onecyclecontrolofswitchingconverter［J］.IEEETransactionsonPowerElectronics，1995，10（6）∶625-633.

［18］SADIKAZ，HUSSAINZM，O'SHEAP.Asingle-bitdigital DC-blockerusingternaryfiltering［C］//IEEETENCON，2005∶1-6.

［19］张宪平，林资旭，李亚西，等.LCL滤波的PWM整流器新型控制策略［J］.电工技术学报，2007，22（2）∶74-77. ZHANGXianping，LINZixu，LIYaxi，etal.Anovelcontrol strategyforPWMrectifierwithLCLfilter［J］.Transactionsof ChinaElectrotechnicalSociety，2007，22（2）∶74-77.

（编辑∶张诗阁）

Inputfilterresonancemitigationschemeformatrixrectifier

LIUXiao1，ZHANGQing-fan2，HOUDian-li3
（1.StateGridofChinaTechnologyCollege，Jinan250002，China；2.SchoolofControlScienceandEngineering，Shandong University，Jinan250061，China；3.SchoolofInformationandElectricalEngineering，LudongUniversity，Yantai264025，China）

∶Inordertomitigateinputfiltersresonance，asimplifiedlow-costcontrolmethod，combinedthe advantagesofone-cyclecontrolstrategyandactivedampingtechnique，wasdevelopedforthree-phase AC-DCmatrixconverter，ormatrixrectifier.Parameterestimatemethodwasusedtoremoveunnecessary sensors.Amodelincludingtheactivedampingmethodandinputfilterwasestablishedwithconsidering delaycausedbyactualcontroller.Aimingtoguidethetuningupofthevirtualresistor，thestabilityof thismodelwasanalyzedusingzero-polemap.Bycombiningwithone-cyclecontrolstrategy，thealgorithm complexityoftheproposedactivedampingmethodwasreduced，resultingineasyengineeringimplementation.Atlast，experimentalresearcheswereconductedonaprototypematrixrectifier.Theresultsshow thatthemagnitudeoftheharmonicsneartheresonancefrequencyisreducedfrommorethan10％tobelow2.5％.Accordingly，theTotalHarmonicDistortion（THD）ofgrid-sideinputcurrentsisdecreased from18.75％to2.5％.Hence，thecorrectnessofthetheoreticalanalysis，andthefeasibilityoftheproposedcontrolmethodarevalidated.

∶matrixrectifier；activedamping；one-cyclecontrol；resonancemitigation

∶TM461

∶A

∶1007-449X（2015）11-0084-08

∶2013-12-09

∶国家自然科学基金（51407088）

∶刘 晓（1979—），男，博士，研究方向为矩阵式整流器以及电力电子装置的非线性控制；

张庆范（1949—），男，副教授，博士生导师，研究方向为电力电子与电力传动、信号处理、自动控制；

候典立（1975—），男，博士，讲师，研究方向为无线功率传输、直流电力线载波通信。

∶刘 晓

DOI∶10.15938/j.emc.2015.11.013