采用I-APSO算法的弛豫响应等效电路参数辨识

蔡金锭，曾静岚，李安娜（福州大学电气工程与自动化学院，福建福州 350116）

采用I-APSO算法的弛豫响应等效电路参数辨识

蔡金锭，曾静岚，李安娜
（福州大学电气工程与自动化学院，福建福州 350116）

∶针对传统弛豫响应等效电路参数辫识方法无法排除试验中充电电压的波动和测量误差所造成的影响，结合去极化电流数据，引入区间-自适应粒子群算法（I-APSO）对油纸绝缘系统进行参数辫识。I-APSO算法不仅在计算过程中减小了实际误差，使结果更为精确，而且能高效率地定位参数解空间。同时考虑现有的介质响应函数未能真实反映实际极化问题，将方根指数衰减规律引入介质响应函数以改进现有的数学模型。最后计算结果表明，相较于传统方法，采用I-APSO算法和改进介质响应数学模型获取的去极化电流曲线与测试曲线更为吻合，通过此算法辫识的等效电路参数能更加真实、有效地反映油纸绝缘系统的极化过程。

∶等效电路；参数辫识；区间—自适应粒子群算法；介质响应函数

0 引言

油纸绝缘电气设备造价昂贵又必不可缺，有效诊断油纸绝缘设备的老化状态，对确保电网经济安全运行具有重要的意义［1-2］。极化去极化电流法是一种揭示绝缘介质极化过程的无损诊断方法，测量的去极化电流曲线内部包含各介质的弛豫信息，其特征量会随着绝缘介质老化程度的加剧而改变，一些学者通过研究介质响应等效电路模型及其参数的变化来间接评估绝缘的老化受潮状态［3-4］。因此，介质响应数学模型和特征参数的准确辨识对评估油纸绝缘老化受潮状态至关重要。

目前基于介质响应函数的等效电路模型参数辨识主要存在以下2个问题∶1）现有的介质响应函数未能反映油纸绝缘介质的实际极化过程，需要改进其数学模型。文献［5］和［6］中的介质响应数学模型是建立在假设偶极子松弛介质间不会相互作用的前提下，基于此介质响应数学模型下计算的参数并不能真实反映实际的极化过程。2）现有的参数计算中未考虑测量误差和充电电压波动的影响。波动的充电电压将引起介质内部电场的变化，从而影响去极化电流曲线，加上测量仪器易受外界电磁干扰而造成测试数据的误差，在此基础上的参数辨识结果并不准确。文献［7］和文献［8］未考虑实际的误差，其参数辨识结果误差较大，不能准确反映油纸绝缘设备老化受潮状况。

基于以上两点，本文将电介质物理学的研究成果——方根指数型衰减规律引人介质响应函数，以贴近实际的极化过程。同时针对测试中充电电压的波动和测量的误差，将I-APSO算法应用到去极化电流函数的参数计算。由于测试数据和充电电压值都在一定的区间范围内波动，故在寻优过程中采用区间算法，并结合粒子群算法的随机搜索性及经验更新能力［9］，从而获取表示为区间集的参数解。其内都包含了考虑各种干扰因素下，实际等效电路参数的可行范围，从而使得辨识结果更加准确。

1 介质响应数学模型的分析和改进

变压器油纸绝缘系统包括绝缘油、隔板、撑条以及油隙，这些介质的弛豫响应速率各不相同，单一弛豫时间的RC等值电路不能反映复合介质的实际极化特性，因此本文采用多个弛豫时间的扩展Debye电路模型［10］，即多个RC支路并联的等效电路来分析油纸绝缘系统的复杂极化过程。扩展Debye模型的等效电路如图1所示。

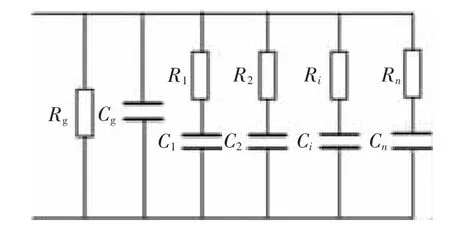
图1 扩展Debye模型的等效电路Fig.1 Dielectricresponseequivalentcircuit basedonextendedDebyemodel

其中，Rg代表绝缘电阻，Cg是工频下的几何电容；极化电阻Ri（i=1，2，…，n）和极化电容Ci（i=1，2，…，n）串联的极化支路代表不同弛豫时间τi=RiCi的弛豫过程。

目前普遍采用以下扩展Debye形式的响应函数f（t）来反映油纸绝缘介质的极化过程，其数学表达式为∶

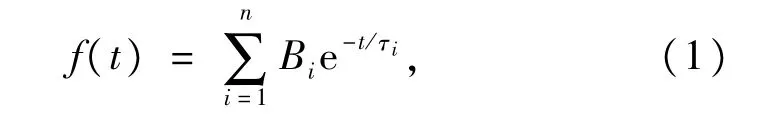
式中∶n表示油纸绝缘介质中弛豫机构的数目；Bi为第i个弛豫机构作用所占的比重；τi表示为第i个弛豫机构的时间常数。

以上介质响应函数是在假设偶极子松弛介质间不会相互作用的前提下获得的［11］，基于此数学模型下计算的参数并不能真实反映实际复杂的极化过程，因此需要一个能准确描述介质极化的数学模型。大量的热释电弛豫数据表明，在不同的情况下电介质具有随机弛豫和自由弛豫的特点，在外加电场下的极化称为随机弛豫，而自由状态下的极化称为自由弛豫，综合考虑以上弛豫特点，弛豫过程将呈现方根指数型衰减规律［12-13］。因此方根指数衰减的介质响应函数更符合实际的弛豫情况，其表达式如下∶

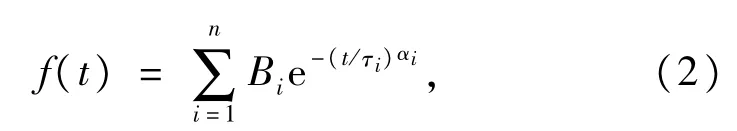
式中∶指数方根αi是线型参数，其中αi∈［0.5，1］。油纸绝缘的介质响应函数可看作由n个弛豫机构的不同方根指数衰减项之和。

去极化电流id与式（2）的介质响应函数之间具有简单的线性关系［5，11］，因此id的表达式如下∶

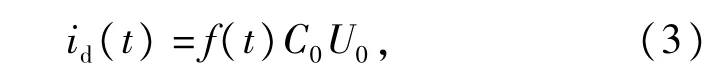
式中∶C0代表油纸绝缘的真空几何电容值；U0为直流的充电电压。

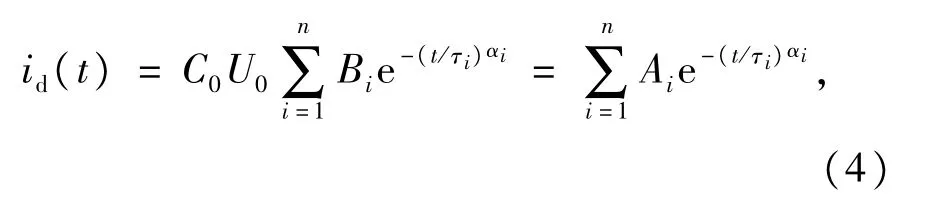
将式（2）的响应函数表达式代人式（3）可得∶其中Ai定义为第i个机构的弛豫贡献系数。在图1的等效电路中，去极化电流特征参数τi和Ai用弛豫机构电路元件参数可表示为∶

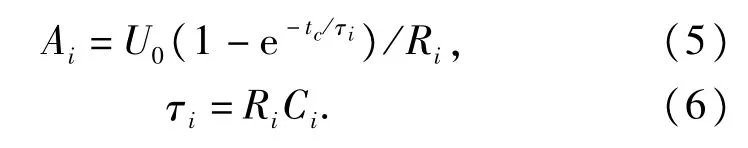
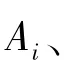
2 I-APSO算法

I-APSO算法将各种误差考虑在内，使得区间参数能直接被包含在计算过程中。本文放弃了传统区间优化的二分定界过程，将区间算法和APSO算法融合，利用了区间的确定性指导和APSO的全局优化能力，有效地求解出参数的可行区间［14］。

2.1 区间粒子种群的初始化

I-APSO算法的独特之处是以区间变量来代替点变量，变量不再是确切的数值，而是包含误差在内的区段。对于一个变量，定义有界闭区间及其特征如式（7）所示。

根据上述区间的定义，第i个粒子的位置矢量xi和速度矢量vi则是一组空间矢量，表达式如下∶

式中D为种群的维数，即未知数的个数，每一维粒子都包含上下区间。

区间粒子位置确定后即可求出各种群中心位置，通过中心选择机制求出最小中心位置作为寻优的方向。同时也将位置区间值代人目标函数，产生适应值区间。

2.2 基于自适应因子的粒子更新

标准的PSO算法容易在寻优过程中陷人局部最优解，引人惯性权重能够有效增强全局和局部搜索的平衡能力［15］。I-APSO算法根据实际搜索情况改变惯性权重，在初期采用较大惯性权重指导全局搜索并加快收敛，在后期采用较小的惯性权重提高局部寻优的能力。自适应惯性权重公式如式（9）所示。

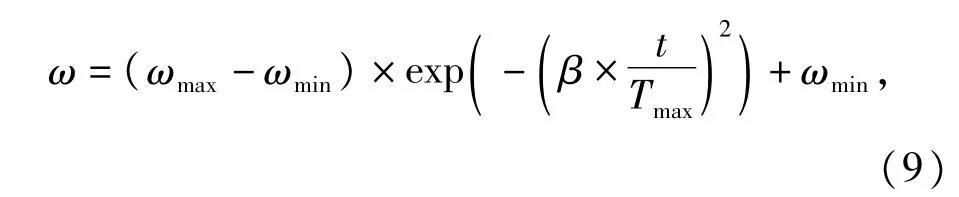
其中∶ωmin和ωmax分别为最小、最大自适应惯性权重；t、Tmax分为当前迭代次数和最大迭代次数；β的取值由经验决定，一般β∈［20，55］。

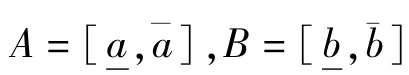
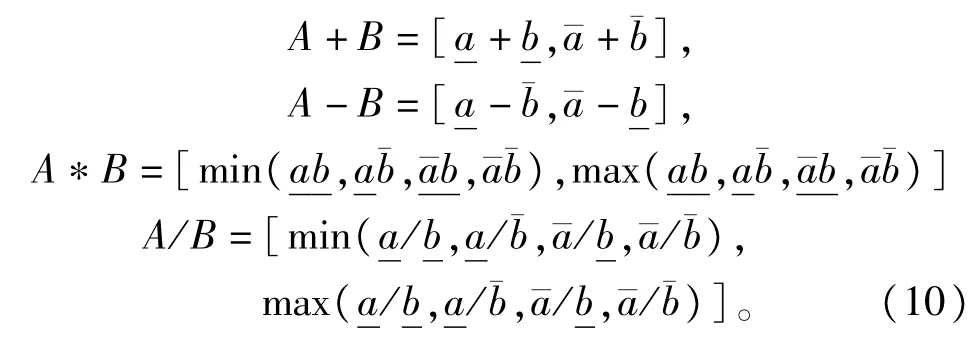
位置和速度的更新按照上述的区间运算法则，更新公式如下∶

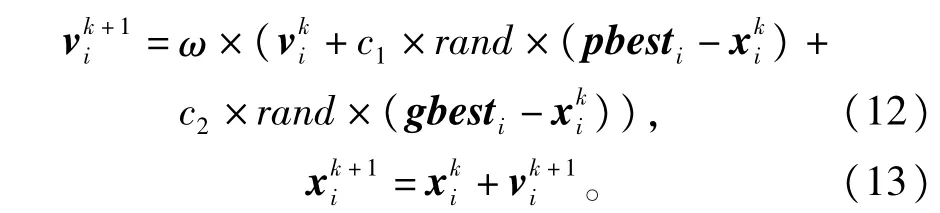
其中∶vi、xi、个体极值pbesti和全局极值gbesti均为区间值，运算遵循区间运算法则；c1、c2为学习因子。

2.3 最优种群缩宽度的缩减

I-APSO算法的核心就是利用区间缩减来代替传统区间算法的二分定界过程。迭代过程中适应值区间宽度不满足精度要求时，为了控制误差应同时缩减pbest宽度，缩减公式如式（14）所示。

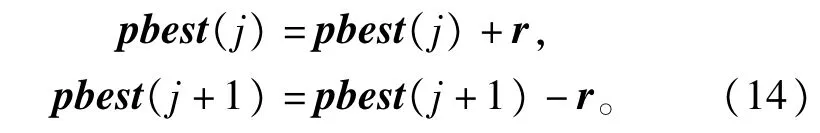
其中∶pbest（j）、pbest（j+1）分别为个体最优区间的上界和下界；宽度r可以是固定值，也可以随着迭代次数的增加而减小。直至确保误差在可控的范围内，最优区间位置宽度满足精度要求。

2.4 I-APSO算法流程

I-APSO算法随着迭代次数的增加，逐步逼近目标函数值的最优解，同时在搜索过程中最优区间也不断缩减，最终缩减到较小宽度的区间里，每一步迭代都体现了区间和粒子群的融合。I-APSO算法流程如图2所示。

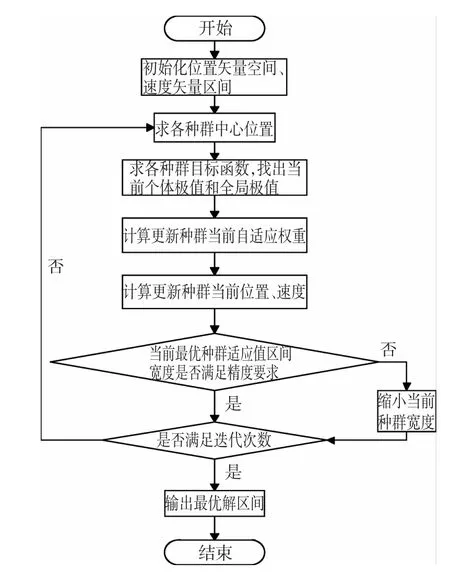
图2 区间-粒子群算法流程图Fig.2 Flowchartofinterval-particleswarm optimizationalgorithm

3 基于I-APSO算法的弛豫响应等效电路区间参数辨识

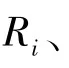
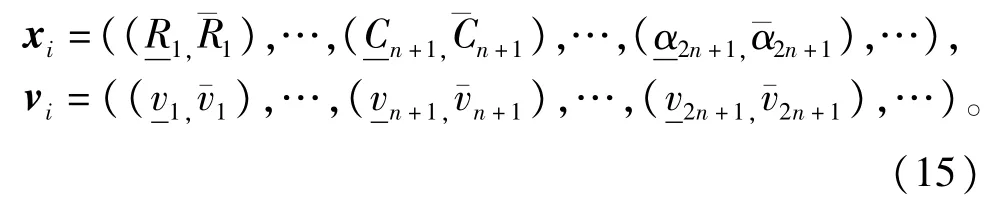
结合式（9）的I-APSO算法权重更新公式，确定每次迭代的权值。在此基础上，再根据式（12）、（13）的粒子位置和速度更新公式即可指引下一次的寻优方向。

3n个未知参数的求解至少需要3n组测量去极化电流数据，联立构成大于3n个方程组如下，其中m（m＞3n）为测量数据的数目。

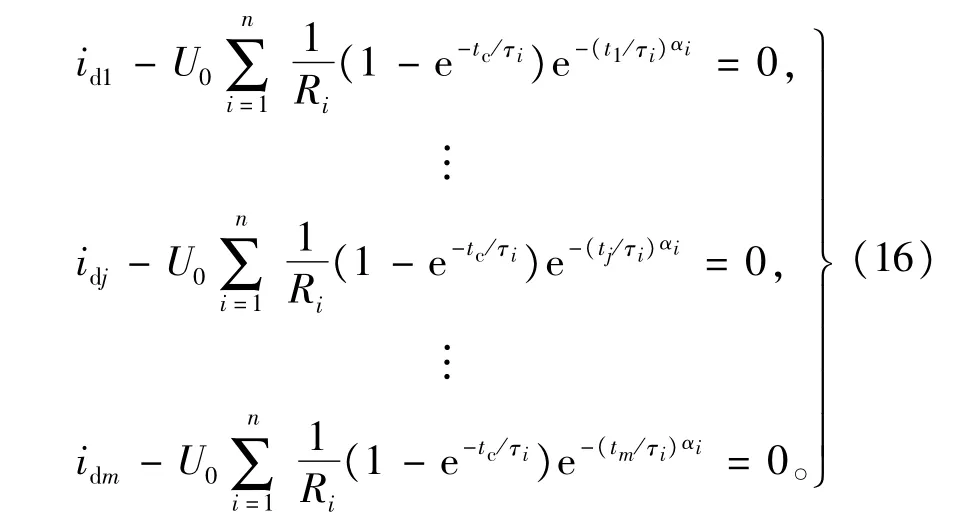
每个粒子都有各自的目标函数适应值以评价当前位置的优劣，故将式（16）的非线性方程组求解转化为最优化问题，构造出的目标函数 F（x）如式（17）所示。

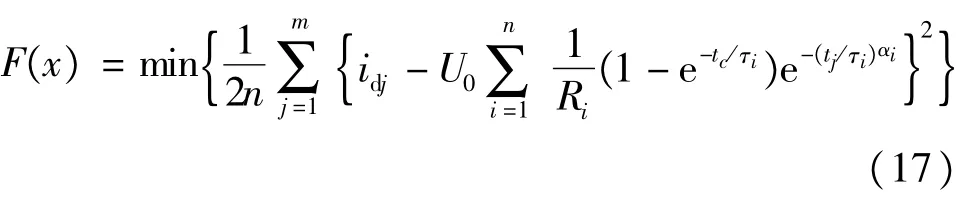
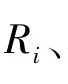
4 实例验证

文献［7］采用微分解析法计算一台电压等级为220kV、容量为240MVA的变压器等效电路参数，原始220kV变压器的扩展Debye模型参数如表1所示。

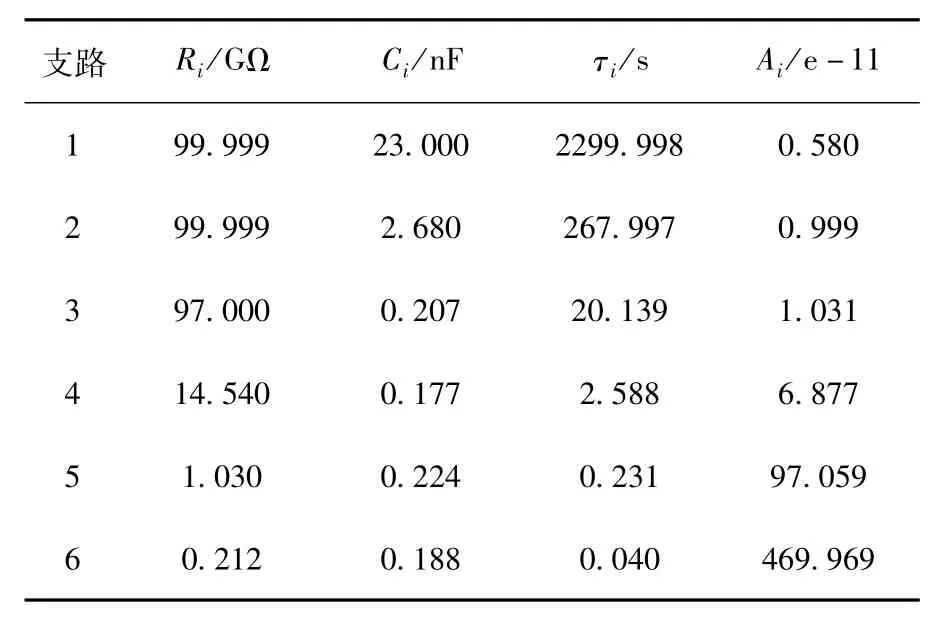
表1 原始220kV变压器的扩展Debye模型参数Table1 ExtendedDebyemodelparametersof 220kVtransformer

文献［7］未考虑充电电压的浮动，而且去极化电流包含噪声干扰，数据波动幅度较大，直接拟合出的参数值并不准确。本文采用改进的介质响应数学模型，同时考虑充电电压和测试值的波动，将I-APSO算法的参数辨识结果和文献［7］进行对比，验证改进的介质响应数学模型的适用性和I-APSO算法的准确性。

根据实际情况，充电电压的波动可取±1V，则U0=［1999，2001］。去极化电流误差取为自身测量值的1％，以确保误差的合理。采用上述介绍的介质响应函数，对文献［7］中的6条极化支路，包含有18个未知数的非线性方程组进行区间优化求解，区间优化结果如表2所示。

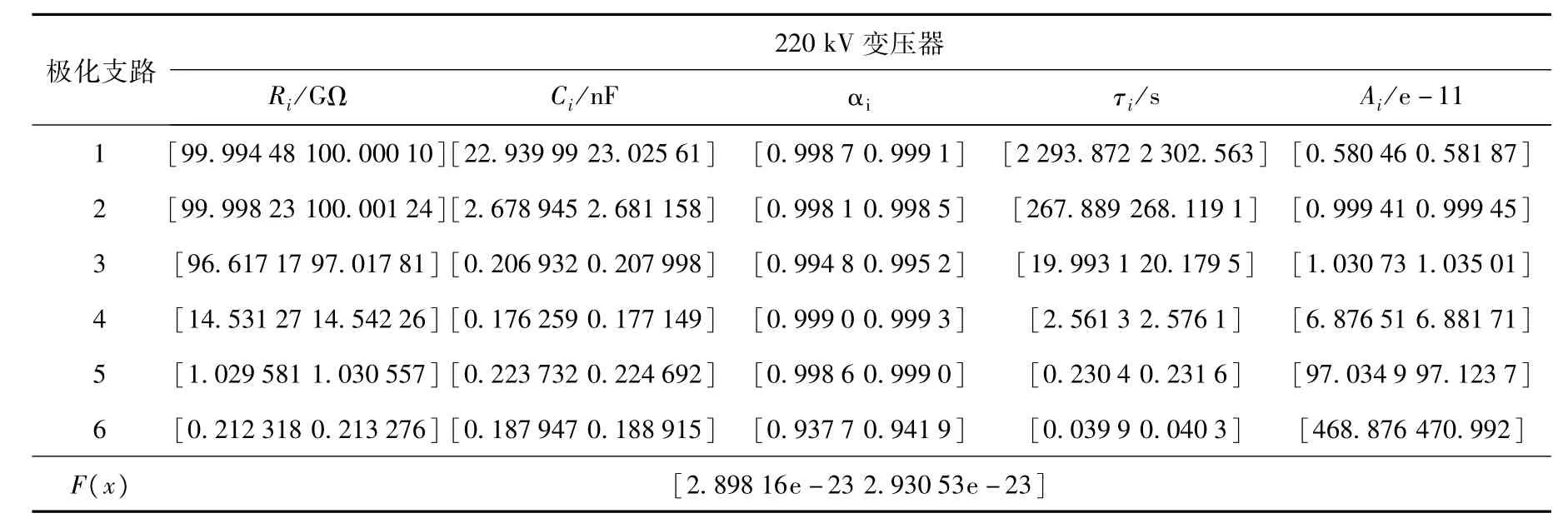
表2 优化求解得到的等效电路参数区间值Table2 Obtainedintervalvaluesofequivalentcircuitparameter

由表2可见，应用改进数学模型，I-APSO算法求出的最优化参数是一个考虑各种误差的最优区间解，参数和Ai最终都收敛至很小的区间。与表1的原始220kV变压器的扩展德拜模型参数相比，每一条支路参数都落在相应的最优区间内部。现定义各条支路参数的最大相对误差如式（18）。

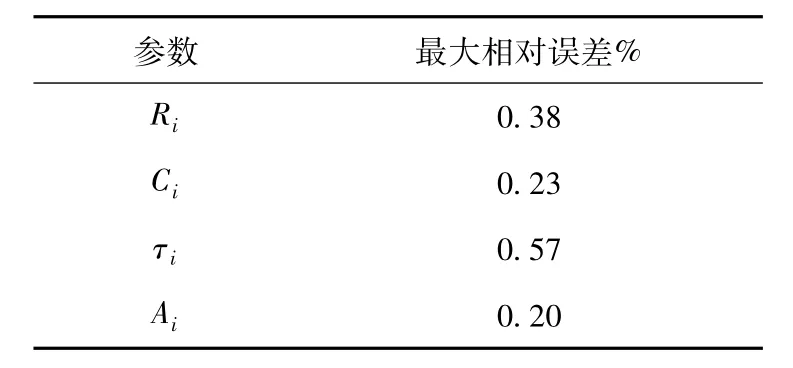
表3 各参数的最大相对误差Table3 Themaximumrelativeerrorof eachparameter

可见考虑实际测量误差和仪器误差后，I-APSO算法求解参数的误差非常小。而文献［7］中时间常数的最大误差达到6.01％，而弛豫贡献系数的最大误差达到11.7％，通过对比说明采用I-APSO算法结果更精确。

采用传统方法求得的参数将是一组固定值，但这一结论过于绝对。因为在实际测量中，直流充电电压总存在一定的波动，并非固定值；同时在高精度的测量过程中，仪器容易受到外界电磁噪声干扰，不可避免地产生误差。采用固定参数值的方法无法剔除以上两方面因素造成的影响。然而，采用I-APSO算法计算得到的等效电路模型参数为最优区间值，其包含了考虑各种干扰因素下的可行解，这样辨识的参数更符合油纸绝缘介质实际的极化情况。

为了进一步验证采用改进介质响应数学模型的适用性和准确性，现将采用改进介质响应函数得到的去极化电流曲线和测试的到去极化电流曲线进行对比。由于每个参数值都是一个区间，求解去极化电流曲线时只要任意代人区间的某个数值即可。现在选取区间的中点、上下端点值分别代人式（4）的去极化电流函数方程，得到去极化电流测量值与计算值对比结果如图3所示。在不同参数取值下，它们的计算值和测量值误差很小，从放大部分可知，区间中点值计算的去极化电流曲线夹在用上下界的计算曲线中，符合区间算法的包含原理［16］。综上所述，采用改进的介质响应数学模型的去极化电流曲线和原测量曲线基本重合，能有效反映油纸绝缘介质的实际弛豫过程。

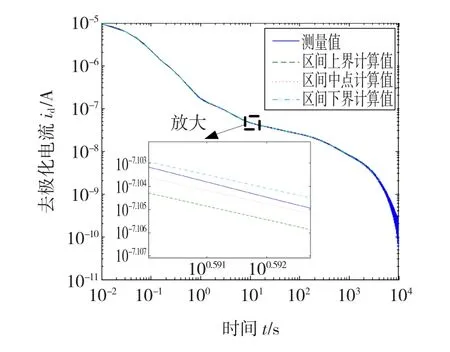
图3 不同参数取值下去极化电流测量值与计算值对比图Fig.3 Comparisonofcalculatedandmeasured valuesunderdifferentparameter

图4给出了传统PSO算法和I-APSO算法计算得到的去极化电流曲线和测试曲线对比结果。

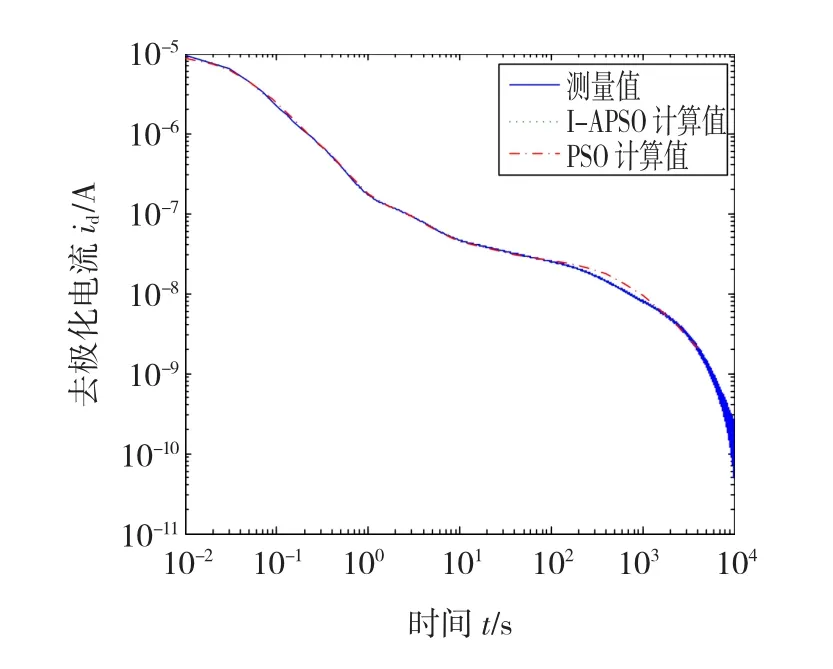
图4 不同算法下去极化电流测量值与计算值的对比图Fig.4 Comparisonofcalculatedandmeasured valuesunderdifferentalgorithms

由图4可见，采用传统PSO算法的计算结果与测量值的吻合度较低，这是由于其计算等效电路参数时没有考虑仪器误差和测试误差，得到的数值解不能反映油纸绝缘实际的极化过程，这给绝缘老化状态的评估带来不确定性。因此相比于POS算法，I-APSO算法的参数辨识结果更为精确。

5 结论

1）在扩展Debye模型的基础上，根据实际电介质的极化情况，引人方根指数型衰减的介质响应函数，改进了数学模型。

2）本文将I-APSO算法应用在极化去极化电流法的参数辨识中，解决了由于充电电压的波动和测试仪器的误差造成参数计算不准确的问题。

3）在上述方法的基础上，采用I-APSO算法解析改进介质响应函数的相关参数。最后通过对比，验证采用改进介质响应数学模型和I-APSO算法解析参数的适用性和准确性。为后续研究变压器绝缘老化与区间电路参数的关系提供了新思路。

∶

［1］林智勇，蔡金锭.油纸绝缘极化等效电路参数计算方法［J］.电机与控制学报，2014，18（8）∶62-66. LINZhiyong，CAIJinding.Novelmethodtocalculatepolarizedequivalentcircuitofoil-paperinsulation［J］.ElectricMachinesand Control，2014，18（8）∶62-66.

［2］王凯，蔡金锭.油纸绝缘变压器非标准极化谱的仿真研究［J］.电机与控制学报，2014，18（9）∶49-53. WANGKai，CAIJinding.Researchonnon-standardpolarization spectrumofoil-paperinsulationtransformers［J］.ElectricMachinesandControl，2014，18（9）∶49-53.

［3］李军浩，司文荣，姚秀，等.油纸绝缘变压器老化状态评估的极化/去极化电流技术研究［J］.仪器仪表学报，2009，30（12）∶ 2605-2611. LIJunhao，SIWenrong，YAOXiu，eta1.Studyofpolarization anddepolarizationcurrentmeasurementsforassessmentofaging stateofoil-paperinsulatedtransformers［J］.ChineseJournalof ScientificInstrument，2009，30（12）∶2605-2611.

［4］SHROFFDH，STANNETTAW.Areviewofpaperaginginpowertransformers［J］.IEEProceedingsCGeneration，Transmission andDistribution，1985，132（6）∶312-319.

［5］SAHATK，PURKAITP.Investigationofpolarizationanddepolarizationcurrentmeasurementsfortheassessmentofoil-paperinsulationofagedtransformers［J］.IEEETransactionsonDielectrics andElectricalInsulation，2004，11（1）∶144-154.

［6］SAHATK，PURKAITP，MULLERF.Derivinganequivalent circuitoftransformersinsulationforunderstandingthedielectric responsemeasurements［J］.IEEETransactionsonPowerDelivery，2005，20（1）∶149-157.

［7］李功新，江修波，蔡金锭，等.采用微分去极化电流法解析变压器油纸绝缘的介质响应函数［J］.高电压技术，2012，38（8）∶1930-1936. LIGongxin，JIANGXiubo，CAIJinding，etal.Dielectricresponsefunctionfortransformeroil-paperinsulationsolvedbymethodofdifferentialdepolarizationcurrent［J］.HighVoltageEngineering，2012，38（8）∶1930-1936.

［8］郭艳雪，蔡金锭.采用时域介电谱线法确定变压器油纸绝缘等效电路参数［J］.供用电，2012，29（6）∶52-62. GUOYanxue，CAIJinding.Equivalentcircuitparameteroftransformeroil-paperinsulationidentifiedbytimedomaindielectric spectrummethod［J］.DistributionandUtilization，2012，29（6）∶52-62.

［9］林国汉，章兢，刘朝华，等.改进综合学习粒子群算法的PMSM参数辨识［J］.电机与控制学报，2015，19（1）∶51-57. LIGuohan，ZHANGJing，LIUZhaohua，etal.ParameteridentificationofPMSMusingimprovedcomprehensivelearningparticle swarmoptimization［J］.ElectricMachinesandControl，2015，19（1）∶51-57.

［10］JOTAAPRS，ISLAMSM，JOTAFG.Modelingthepolarizationspectrumincompositeoil/paperinsulationsystems［J］. IEEETransonDielectricsandElecInsulation，1999，6（2）∶145 -151.

［11］张涛.基于回复电压特征量的变压器油纸绝缘状态诊断研究［D］.福州∶福州大学电气工程与自动化学院，2010∶33 -36.

［12］李景德，曹万强，李向前，等.时域介电谱方法及其应用［J］.物理学报，1996，45（7）∶1225-1231. LIJingde，CAOWangxiang，LIXiangqiang，etal.Timedomain dielectricspectroscopymethodanditsapplication［J］.Acta PhysicaSinica，1996，45（7）∶1225-1231.

［13］沈韩.时域介电谱的非典型线型［J］.中山大学研究生学刊自然科学版，1997，18（4）∶4-8. SHENHan.Non-typicallineshapeoftimedomaindielectric spectroscopy［J］.NaturalScienceJournaloftheGraduatesSun Yat-senUniversity，1997，18（4）∶4-8.

［14］关守平，房少纯.一种新型的区间-粒子群优化算法［J］.东北大学学报，2012，33（10）∶1381-1384. GUANShouping，FANGShaochu.Newinterval-particleswarm optimizationalgorithm［J］.JournalofNortheasternUniversity，2012，33（10）∶1381-1384.

［15］赵志刚，常成.自适应混沌粒子群优化算法［J］.计算机工程，2011，37（15）∶128-130. ZHAOZhigang，CHANGCheng.Adaptivechaosparticleswarm optimizationalgorithm［J］.ComputerEngineering，2011，37（15）∶128-130.

［16］胡承毅，徐山鹰，杨晓光.区间算法简介［J］.系统工程理论与实践，2003，23（4）∶59-62. HUChengyi，XUShanying，YANGXiaoguang.Abriefintroductiontotheintervalmethods［J］.SystemsEngineering-Theoryand Practice，2003，23（4）∶59-62.

（编辑∶张诗阁）

Parameteridentificationforequivalentcircuitofrelaxationresponse basedoninterval-activeparticleswarmoptimizationalgorithm

CAIJin-ding，ZENGJing-lan，LIAn-na
（CollegeofElectricalEngineeringandAutomation，FuzhouUniversity，Fuzhou350116，China）

∶Aimingattraditionalmethodofparameteridentificationforrelaxationresponseequivalentcircuit，whichcannoteliminatefluctuationsofchargingvoltageandmeasurementerror，combinedwithdepolarizingcurrentdata，theinterval-adaptiveparticleswarmoptimization（I-APSO）wasintroducedtoidentifytheparametersofoil-paperinsulation.Thealgorithmnotonlyreducestheactualerrormakingthe resultmoreprecise，butalsolocatestheoptimalsolutionareasoftheparameterseffectively.Theradical exponentialdecaylawwasusedtoimproveddielectricresponsefunctionconsideringthattheexistingone cannotreflectthemediumdepolarizationprocessaccurately.Theresultshowsthatdepolarizingcurrent curvebyI-APSOandimproveddielectricresponsemodelcanbematchedbetterwithtestcurvecompared withconventionalmethod，whichreflectsthedielectricprocessofoil-paperinsulationsystemmoretruly andeffectively.

∶equivalentcircuitmodel；parameteridentification；interval-activeparticleswarmoptimization algorithm；dielectricresponsefunction

∶TM411

∶A

∶1007-449X（2015）11-0078-06

∶2014-11-05

∶国家自然科学基金（61174117）

∶蔡金锭（1954—），男，博士，教授，博士生导师，研究方向为人工智能技术在电力工程中的应用研究；

曾静岚（1990—），女，硕士研究生，研究方向为电力变压器油纸绝缘故障诊断；

李安娜（1988—），女，硕士，研究方向为电力变压器油纸绝缘故障诊断。

∶蔡金锭

DOI∶10.15938/j.emc.2015.11.012