一种感应电机预测控制的电流静差消除方法

金辛海，张扬，杨明，徐殿国（.哈尔滨工业大学电气工程系，黑龙江哈尔滨 5000；.上海辛格林纳新时达电机有限公司，上海080）

一种感应电机预测控制的电流静差消除方法

金辛海1，张扬2，杨明1，徐殿国1
（1.哈尔滨工业大学电气工程系，黑龙江哈尔滨 150001；2.上海辛格林纳新时达电机有限公司，上海201801）

∶感应电机电流预测控制可以有效避免由电流环中各个滞后环节所导致的控制性能恶化，提高电流控制的动态性能。但由于测量误差以及参数变化等原因，预测控制器所使用的感应电机模型参数与实际电机参数很有可能存在偏差，进而引起电流静差，导致系统效率降低，无法输出额定转矩及无法工作在转矩控制模式等问题。在感应电机模型基础上，定量分析了预测控制模型参数误差对电流控制稳定性的影响，并推导出电流指令与实际反馈电流的静差与模型参数误差两者之间的定量关系，进而提出一种电流静差消除方法。这种方法通过d、q轴反馈电流对预测控制模型参数进行校正，来消除控制器电机模型参数误差所引起的静差。最后通过实验验证了此种方法的可靠性和有效性。

∶预测电流控制；感应电机；参数校正；电流静差消除

0 引言

感应电机具有低成本、高可靠性等优点，广泛应用在工业各个领域。基于空间矢量脉宽调制的控制系统一般采用双闭环结构，外环为速度环，内环为电流环，电流控制器以指令电流和实际反馈电流为输人，经过计算生成目标电压指令。目前感应电机变频器广泛采用数字比例积分调节器（proportionintegration，PI）作为电流控制器［1］。由于数字控制系统固有的采样保持和量化环节，以及脉宽调制（pulse widthmodulation，PWM）占空比更新、逆变器的输出、死区和各种滤波等延时环节，限制了系统动态响应速度的提升。

与传统数字PI控制相比，预测控制可以获得更好的动态响应性能，其关键在于预测控制能够实现在当前控制周期下，预测出下一周期的控制指令，从根本上解决数字PI控制的延迟滞后。

目前，预测控制理论可以分为系统模型预测［2-3］、动态矩阵预测［4-5］、广义预测控制［6-7］以及内模控制［8-12］等多个不同的控制算法。文献［8-11］提出了将7种不同的电压矢量输人到预测模型中求出7个预测电流，再将预测电流与指令电流输人到评价函数中进行比较，进而确定唯一的电压矢量作为输出电压指令。这种方法的优点是电流频响快，缺点是电流纹波较大。文献［13］采用了模型参考自适应、预测控制以及神经网络自学习相结合的控制系统，但是该方法，计算量很大，对CPU的计算能力要求很高。文献［14］分别研究了基于三电平逆变器的预测电流矢量控制和预测磁链直接转矩控制，文中分别对两种控制方式下的预测控制器进行了设计。

电流预测控制能够使电机电流获得良好的动态响应，但是也存在一定的问题。由于预测控制是基于模型的控制方法，因此在控制器中需要准确地使用电机模型的电阻、电感等参数。而在实际系统中，这些参数测量很可能存在误差，并且电机电感会随着电机工作状态而改变，尤其是当电机负载较大时，电机电感值由于饱和特性而发生变化，模型参数与实际参数的误差会使电流控制出现振荡或静差［15］。电流振荡会导致电机机械振荡及驱动器过流报警，而电流静差会导致驱动系统效率降低、额定转速下无法输出额定转矩及无法工作在力矩控制模式等很多问题。因此需要适当地改进算法，提高电流预测控制的鲁棒性并消除电流静差。

文献［16］提出一种鲁棒性控制方法，可以解决电感参数过大所导致的系统振荡，但这种方法没有考虑电感参数误差对电流静差的影响。文献［17］为了消除参数误差的负面影响，使用PI控制d轴电流，并在q轴电流预测控制中加人积分环节，虽然能够消除电流静差，但由于积分饱和的影响已经严重削弱了预测控制在动态性能方面的优势。文献［18］采用了模型参考自适应的方法，对电机的电感等参数进行在线参数辨识，但是需要占用大量的系统资源。

本文将以感应电机数学模型为基础，分析数字PI控制器限制系统频响进一步提升的原因，提出一种基于模型的感应电机电流预测控制算法，能够在当前控制周期内预测出下一个周期的指令电压，并进一步定量分析了预测控制模型参数误差对电流控制稳定性的影响，并推导出电流指令与实际反馈电流的静差与模型参数误差两者之间的定量关系，进而提出一种有效消除电流静差方法。

1 感应电机数学模型

在d-q同步旋转坐标系下，采用间接矢量控制（假设转子总磁链矢量沿着d轴方向，即转子磁链只存在于d轴）方式的感应电机的定子电压方程如下所示。

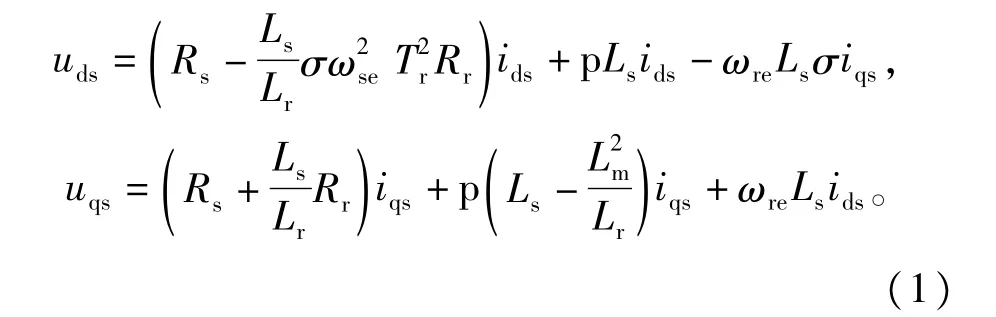
式中∶uds、uqs是定子d、q轴电压，ids、iqs是定子d、q轴电流，Rs、Rr是定、转子电阻，Ls是定子电感，Lr是转子电感，Lm是定转子互感，p是微分算子，ωse是定子电角速度，ωre是转子电角速度，σ是漏磁系数，σ=1-L2m/LsLr，Tr是转子时间常数，Tr=Lr/Rr。

为后续推导过程方便，式（1）简化写成状态方程形式（2）

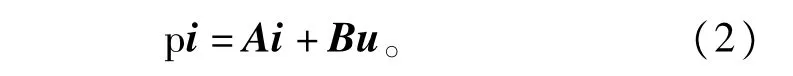
其中i=［idsiqs］T，u=［udsuqs］T，

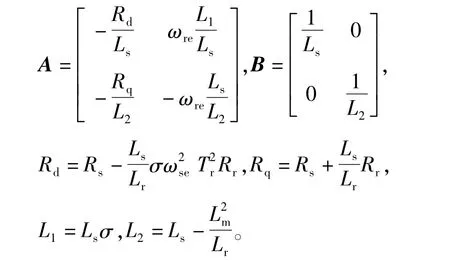
2 传统PI控制

由于PI控制器有结构简单，成熟可靠等优点，感应电机的传统电流控制通常采用PI控制结构，结构框图如图1所示。

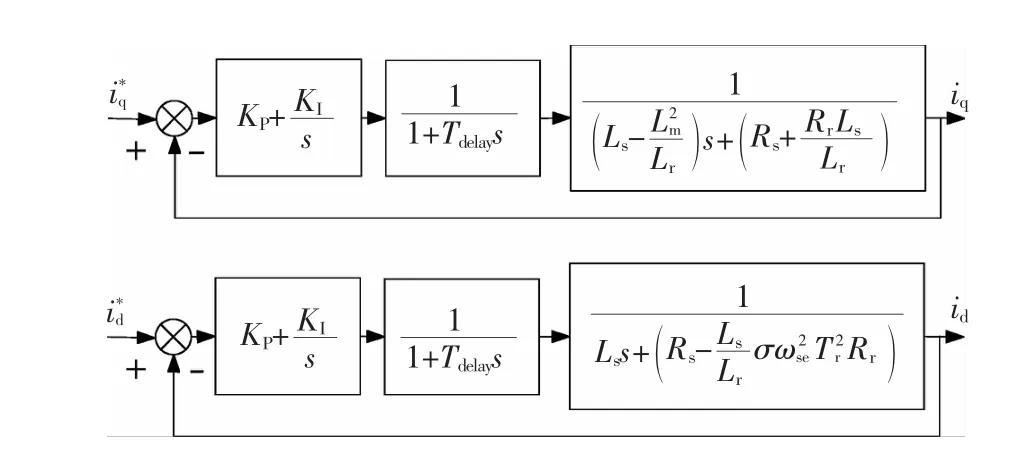
图1 电流环控制框图Fig.1 Diagramofcurrentcontrolloop

这样得到的电流环iq开环传递函数如下式∶

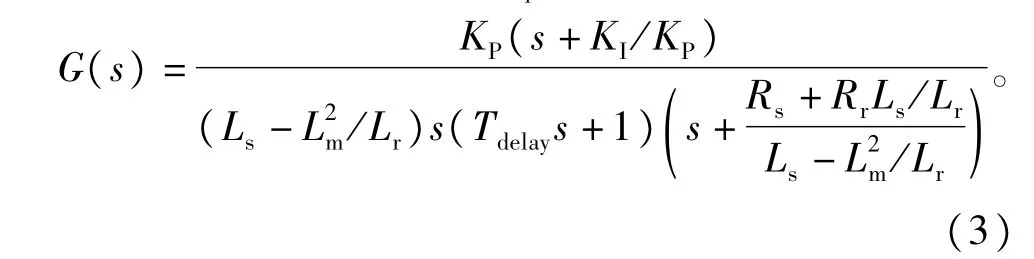
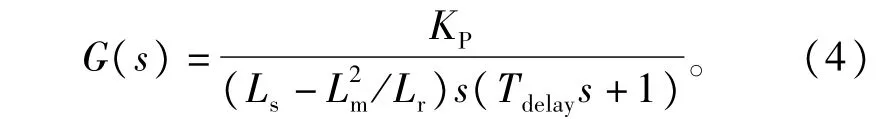
根据Ⅱ阶系统的频域分析理论可知，当系统的开环截止频率ωc=Kp/（Ls-L2m/Lr）小于1/Tdelay并留有裕量时，系统可以保持稳定。

由此可见电流环的带宽拓展的最主要限制条件是Tdelay，Tdelay包括电流采样延时、脉宽调制占空比更新延时、逆变器的输出、死区、滤波延时，Tdelay一般等于电流环的采样控制周期，逆变器的载波频率一般在2～10kHz，即Tdelay在100～500μs之间。系统ωc设定值越大，电流环带宽就越高。id的PI控制与iq的原理是相同的，这里不再赘述。

3 电流预测控制

为了设计电流预测控制器，需要将电机的状态空间函数进行离散化，由于采样保持周期T很小，在采样周期内电机的ωre相当于常数，由式（2）可得等效离散化方程为

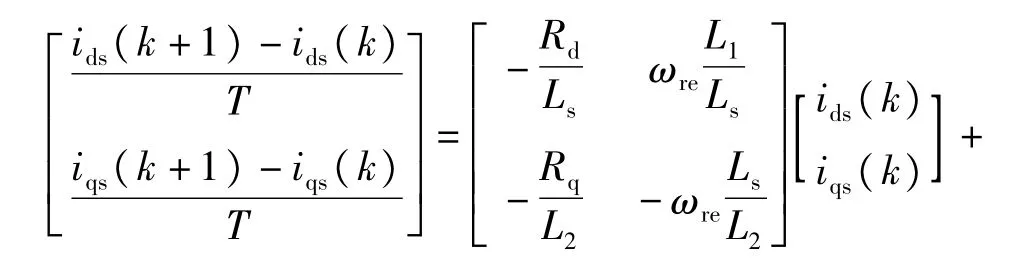
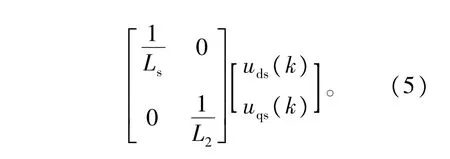
整理得到

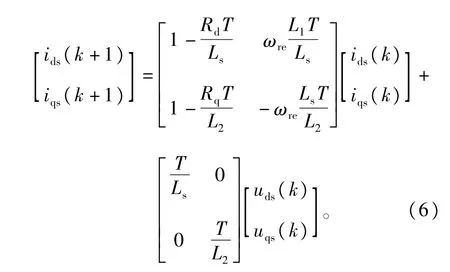
求逆，整理得到

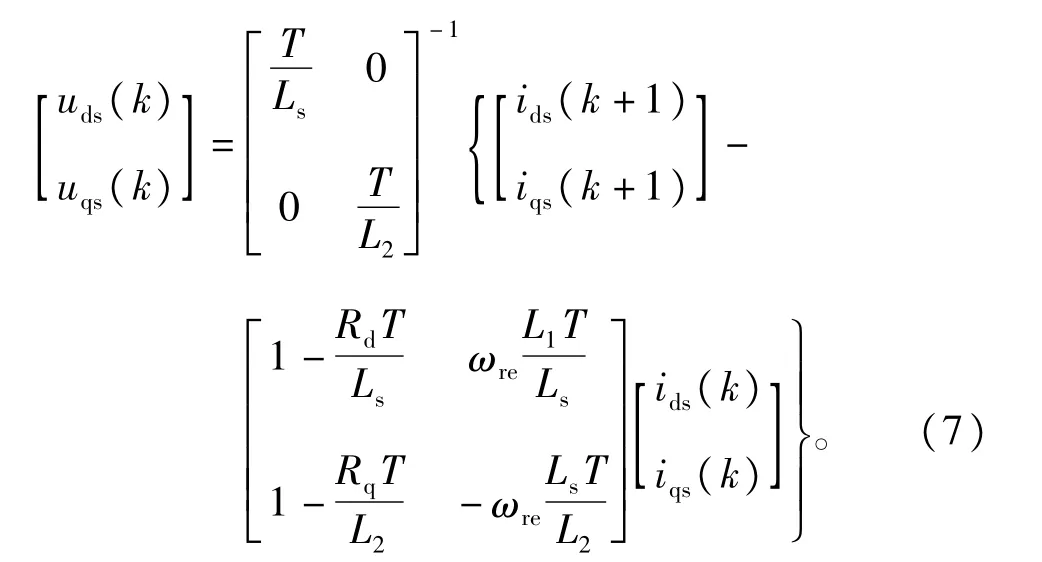
把上式化简得到下式

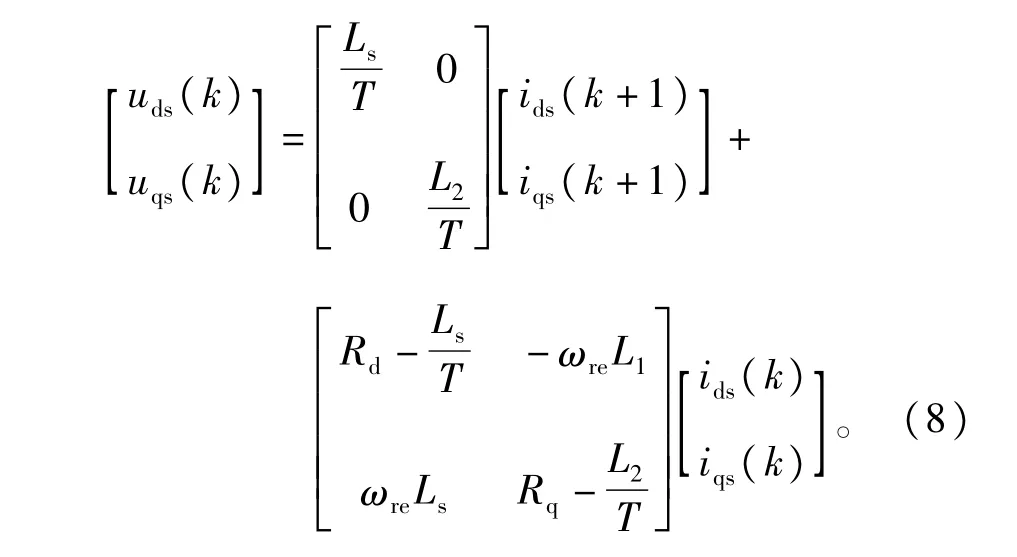
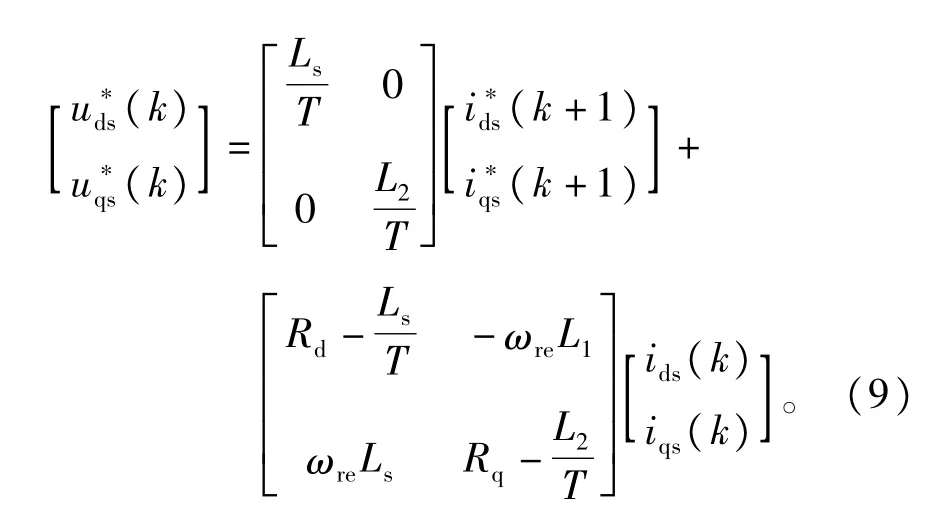
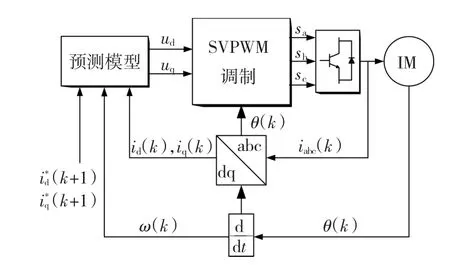
图2 电流预测控制结构图Fig.2 Blockdiagramofpredictivecurrentcontrol

上述控制过程的第k和k+1中断周期控制框图如下，式（9）就是图3中的电流预测控制器使用的计算公式。

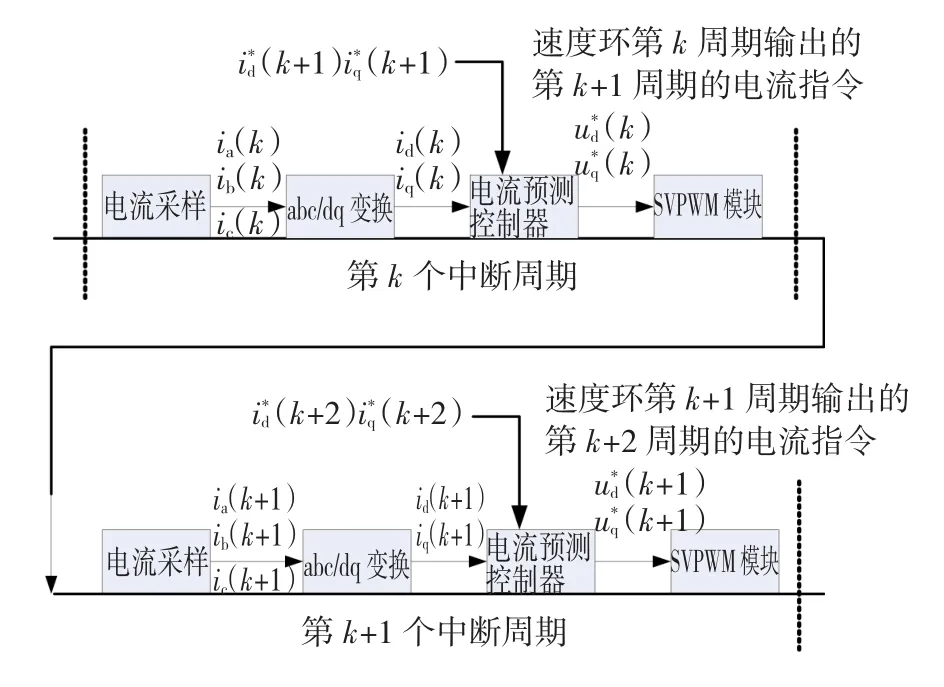
图3 控制周期框图Fig.3 Diagramofcontrolsequence

4 模型参数误差分析

4.1 参数误差的影响

1）参数L2误差对稳定性影响

假设电流预测控制器中L2有误差，即实际的电机电感是L2，控制器使用的电感参数是L'2，将L'2替换L2代人式（9）的uqs部分，得到

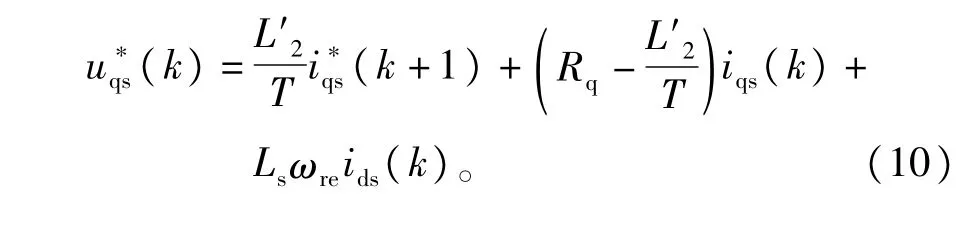
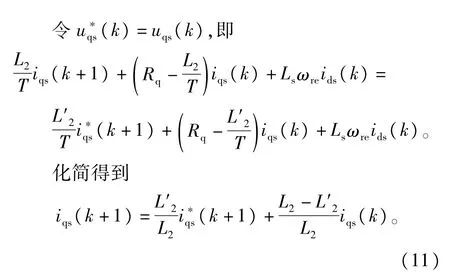
将式（11）转换成Z离散域传递函数如下

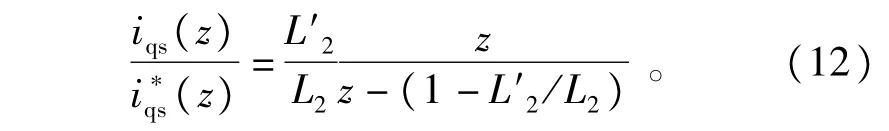
由式（12）得系统的特征根为z=1-L'2/L2，离散域根轨迹如图4所示，离散控制系统稳定的充要条件是系统的极点在z平面的单位圆内，即∶

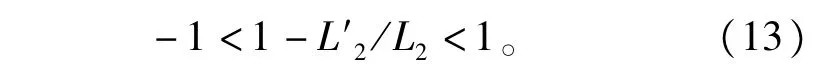
由式（13）可得系统稳定条件为0＜L'2＜2L2，即预测控制器使用的参数L'2小于实际参数L2的2倍的条件下，系统可以保持稳定。一般情况下，参数的误差会在2倍以内，所以系统的稳定性是可以得到保证的。

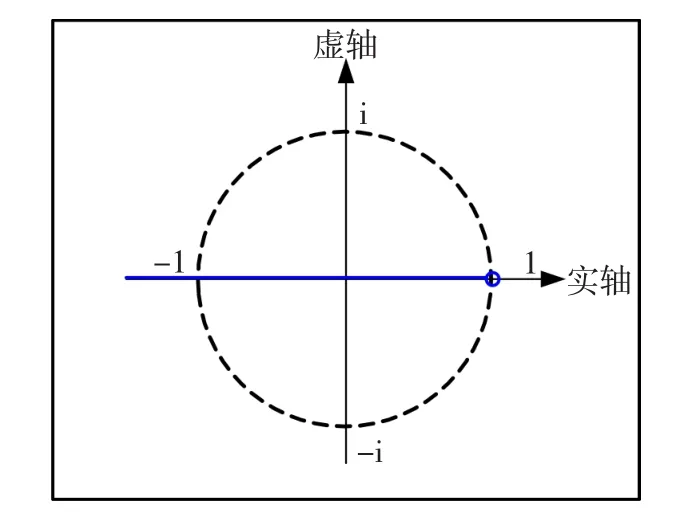
图4 离散域根轨迹Fig.4 Rootlocusofdiscretedomain

2）参数L2误差对静差影响

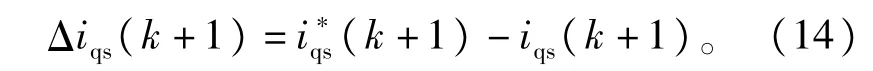
把式（14）代人式（11）中，得到式（15）

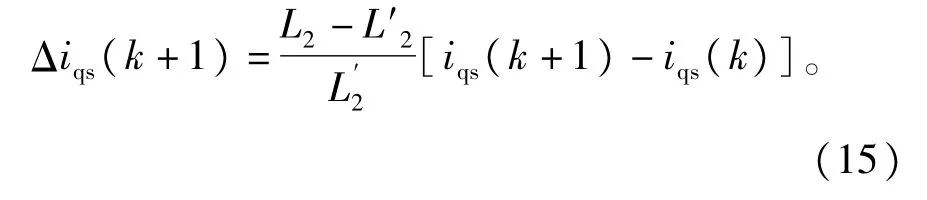
因为采样控制周期时间很短，所以iqs（k+1）-iqs（k）趋近于0，所以Δiqs（k+1）很小，即L2参数的偏差对于iqs静差的影响很微弱。采样控制周期T越小，对于减小iqs静差越有利。

3）参数Rq误差对稳定性影响

假设电流预测控制器中Rq有误差，即实际的电机参数是Rq，控制器使用的电机参数是R'q，ΔRq= Rq-R'q，将R'q替换Rq代人式（9）的uqs部分，得到

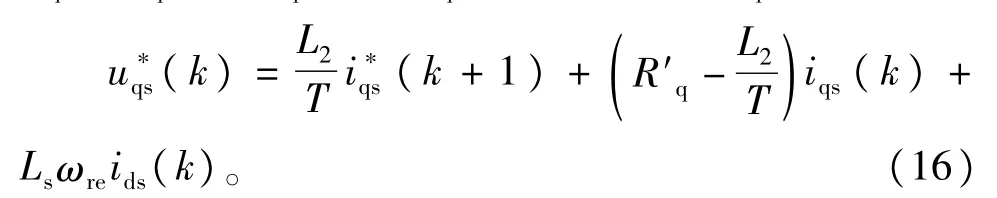
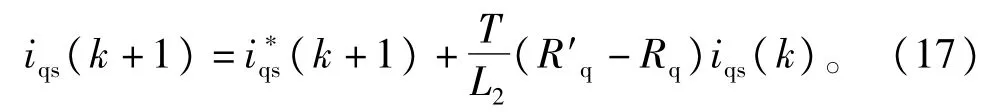
转换成离散域传递函数

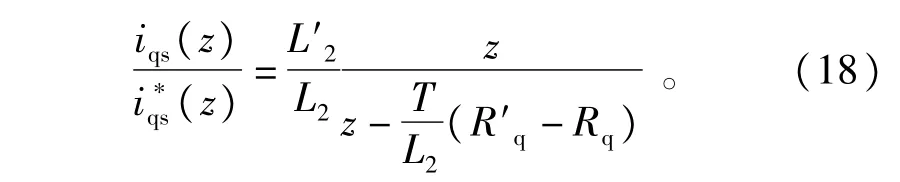
由离散域系统稳定判据可知，系统的极点在z平面的单位圆内时系统稳定，即图5中的根轨迹在单位圆内。

可得，满足Rq-L2/T＜R'q＜Rq+L2/T条件时，系统稳定。

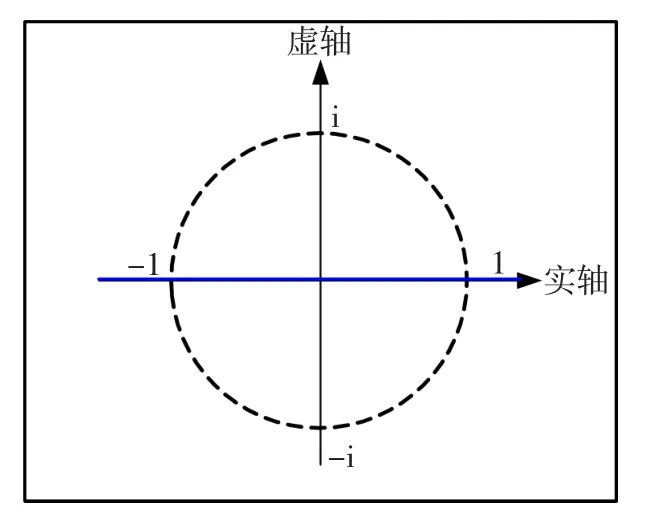
图5 离散域根轨迹Fig.5 Rootlocusofdiscretedomain

4）参数Rq误差对静差影响

将式（14）代人式（17）得到式（19）

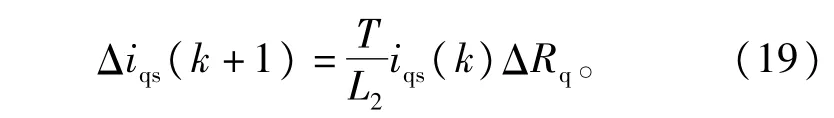
可见，Δiqs（k+1）与ΔRq成正比例，当iqs（k）接近于0时，即电机处于空载运行时，Δiqs（k+1）也接近于0。换句话说，电机空载运行时，即便iqs的实际电流与指令电流之间有偏差，也不是由于ΔRq导致的。

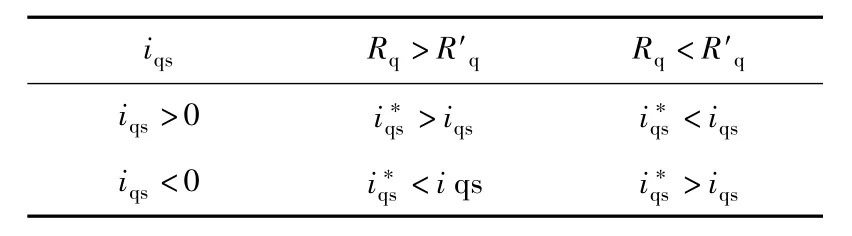
表1 Rq参数偏差与电流静差Table1 Rqparametererrorandcurrenterror

5）参数Ls误差对稳定性影响

假设电流预测控制器中Ls有误差，即实际的电机参数是Ls，控制器使用的电机参数是L's，ΔLs=Ls-L's，将L's替换Ls代人式（9）的uqs部分，并按照类似前面的思路化简得到式（20）

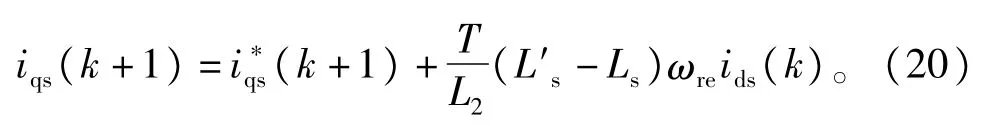
由式（20）可见当Ls有偏差时，是不会引起iqs控制发散的。

6）参数Ls误差对静差的影响

把式（14）代人式（20）得到式（21）

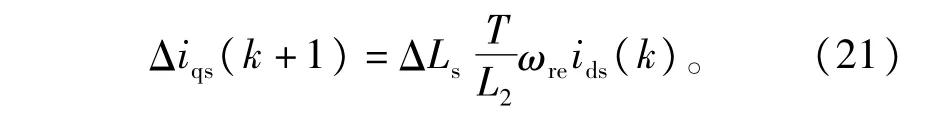
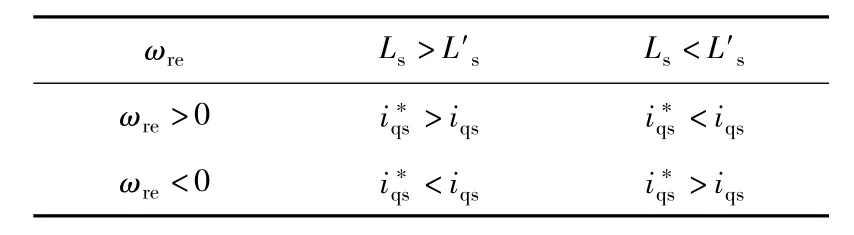
表2 Ls参数偏差与电流静差Table2 Lsparametererrorandcurrenterror

式（9）中的uds部分与uqs部分本质上是一致的，uds的L1相当于上面分析的Ls，uds的Rd相当于上面所分析的Rq，uds的Ls相当于上面分析的L2，所以这里就不再赘述了。

4.2 电流静差消除

由上面的分析可知，预测控制器的Ls与Rq的参数偏差都会导致iqs指令与实际电流有静差，当电机空载运行时，iqs的静差是由Ls的偏差ΔLs引起的，与Rq无关。考虑到iqs静差与Ls的偏差成正比，并且随着ωre越大，iqs的静差也越大的特性，使电机空载额定转速运行，通过iqs电流静差来调整预测控制器中的L's参数，以最终消除iqs电流静差。本文采用加人积分的方法使预测控制器的L's最终收敛到真实值，如下式所示

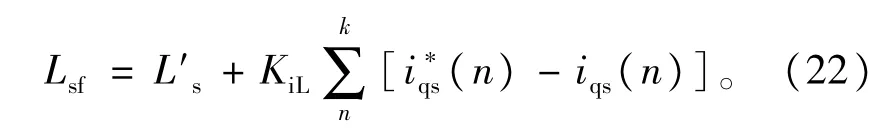
其中∶Lsf是控制器Ls参数的最终收敛值，也就是电机的真实Ls值；L's是控制器中Ls初始值，也就是未经过调整的Ls值；KiL是积分系数。

当Ls参数最终收敛到电机的真实值后，当电机运行在恒定负载条件下时，如果iqs有电流静差，这是由控制器R'q的偏差ΔRq导致的。同样采用加人积分的方法使预测控制器的R'q最终收敛到真实值，如下式所示

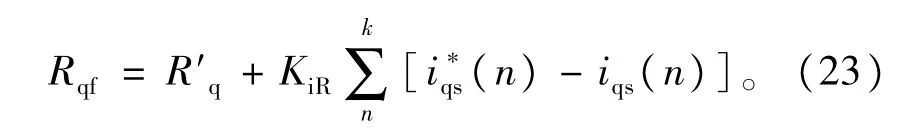
其中∶Rqf是控制器Rq参数的最终收敛值，也就是电机的真实Rq值；R'q是控制器中Rq初始值，也就是未经过调整的Rq值；KiR是积分系数。图6是加人静差消除算法的改进电流预测控制结构框图。

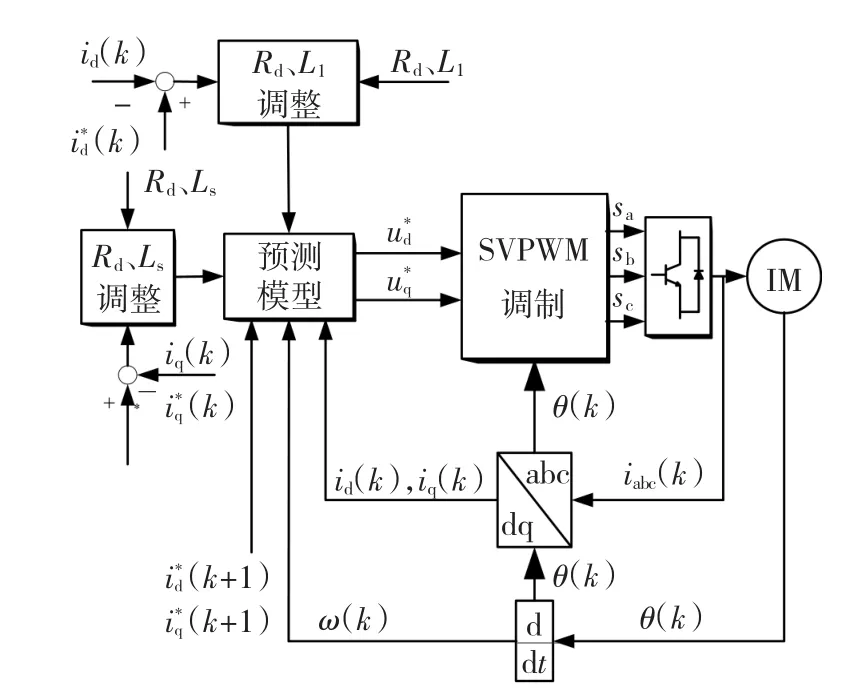
图6 加入静差消除算法的电流预测控制结构框图Fig.6 Predictivecurrentcontrolwithstatic erroreliminationalgorithm

5 实验结果和分析

本文采用变频器驱动11kW感应电机进行实验验证，用磁粉制动器提供负载转矩，电机的参数如下表3所示。变频器采用ST公司的ARM芯片来实现控制算法，芯片型号为STM32F103，主频为72MHz，功率开关管的开关频率为6kHz。

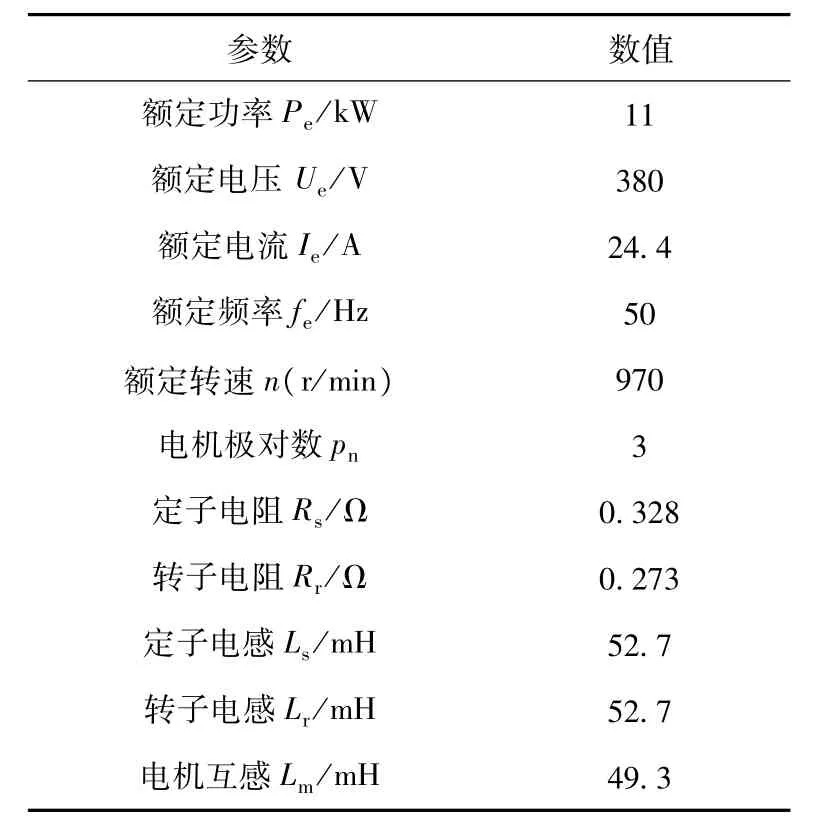
表3 感应电机参数Table3 RatingsandparameterofACmotor

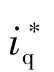
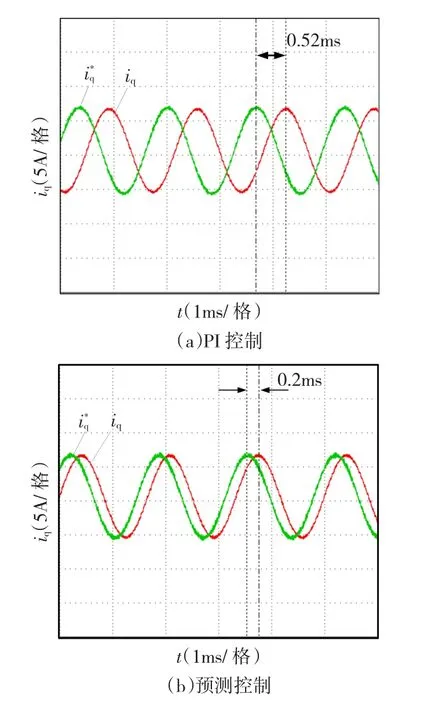
图7 电流环频响测试Fig.7 Frequencyresponseofcurrentcontol

表4 预测控制电流环频响测试表Table4 Frequencyresponseofpredictivecurrentcontrol

图8是预测控制与PI控制的电流阶跃响应对比实验，可见PI控制的实际电流超调量较大，稳定时间较长，而预测控制的超调量和稳定时间都较小，两者的上升时间基本相同。通过调整PI控制参数，可以减少超调量，但是那样上升和稳定时间都会延长很多，对于PI控制来说，缩小超调量和缩短上升和稳定时间是相互矛盾的，但是预测控制可以较好的同时兼顾超调量和调整时间。

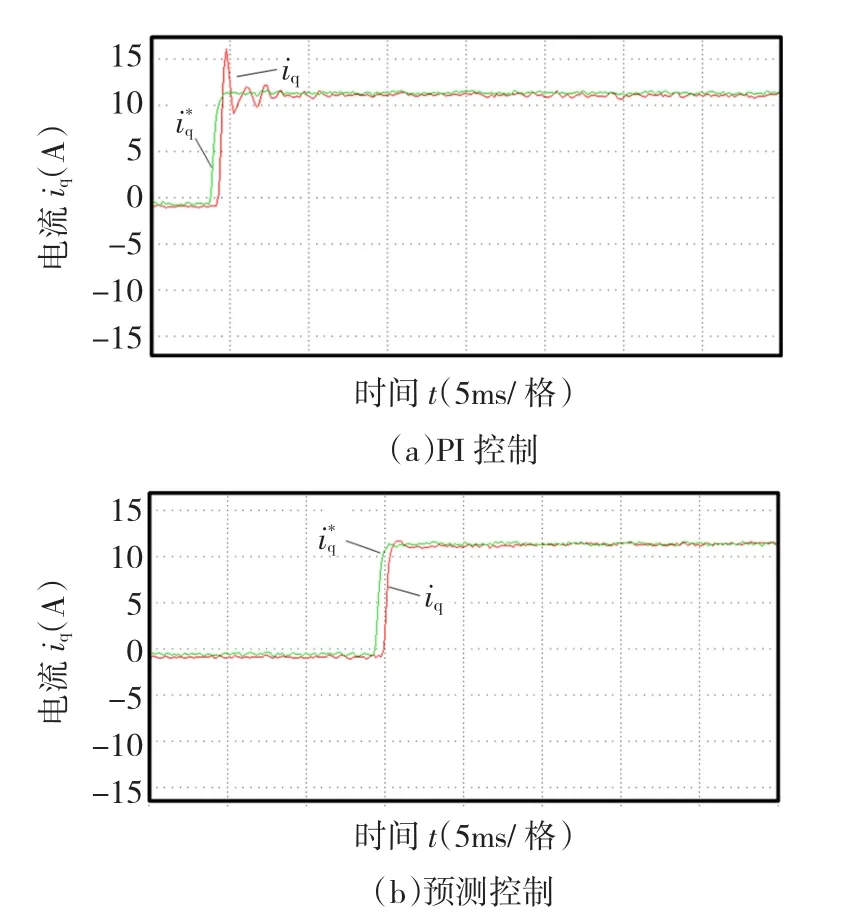
图8 电流阶跃响应对比实验Fig.8 Diagramofstepcurrentresponse

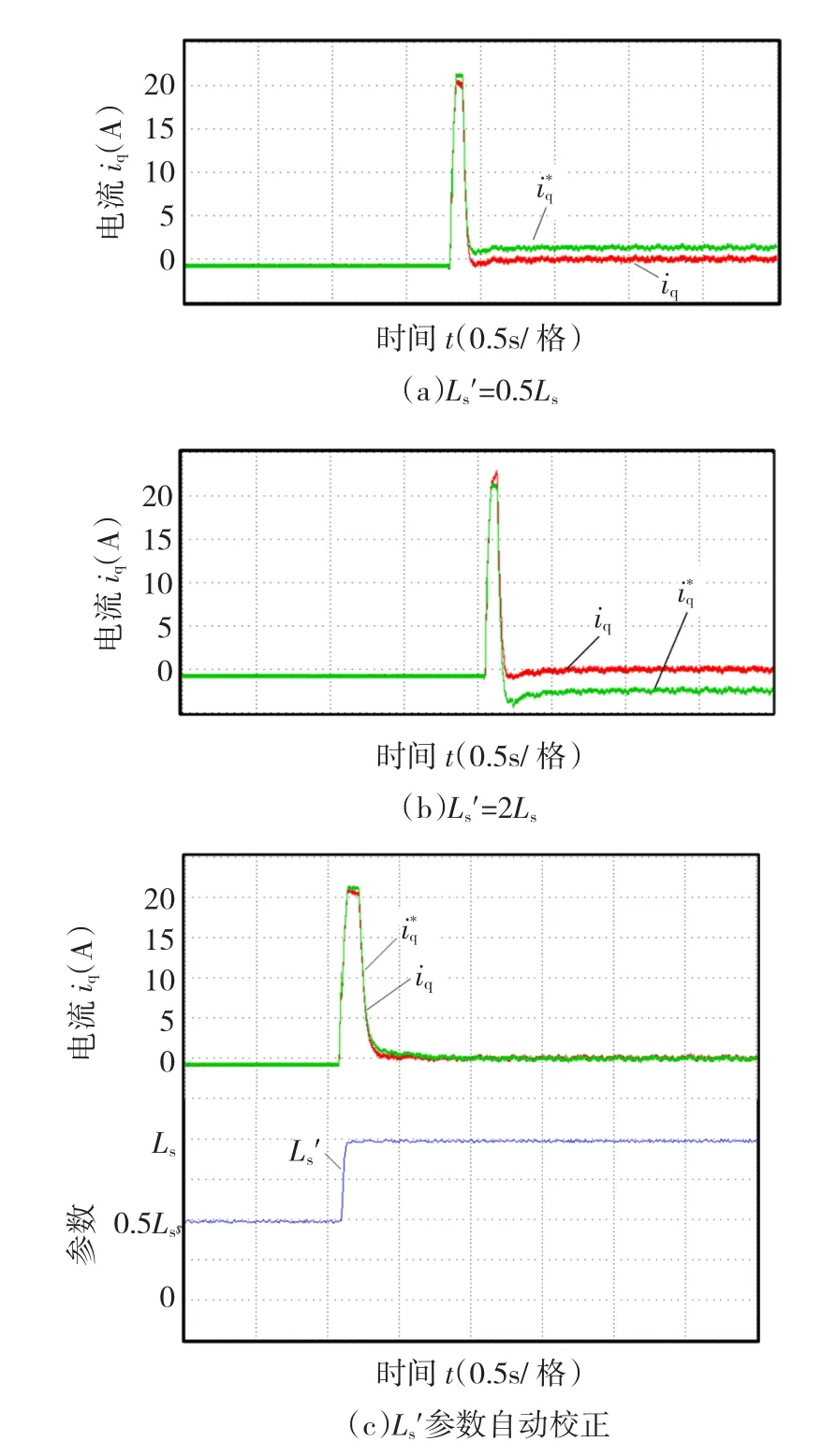
图9 预测控制参数L's校正实验Fig.9 PredictivecontrolparameterL'scorrection

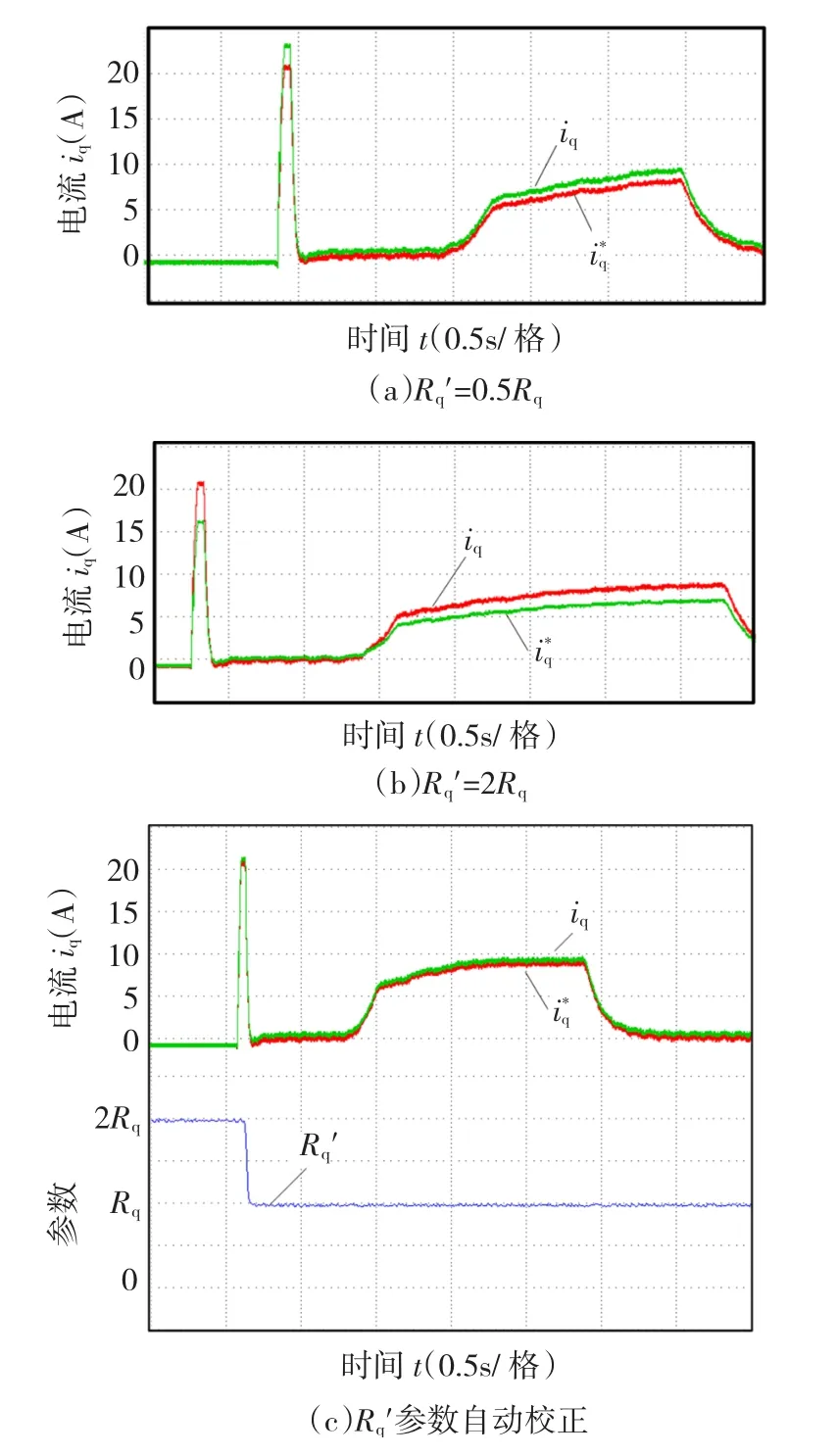
图10 预测控制参数R'q校正实验Fig.10 PredictivecontrolparameterR'qcorrection

综上所述，实验证明预测控制的动态响应特性比PI控制更好，预测控制器的参数自校正算法可以有效消除电流指令与实际电流之间的静差。

6 结论

本文提出了一个基于感应电机模型的电流预测控制方法。首先分析了传统PI控制器对电流环带宽提升的限制因素，然后给出了本文电流预测控制的理论推导过程和依据。定量分析了预测控制器所使用的电机模型参数与实际电机参数有偏差的条件下，会对控制的稳定性产生不良影响，还会导致电流指令与实际电流反馈之间产生静差，基于上述定量分析提出一种预测控制器的模型参数校正方法，可以有效消除电流静差。通过实验结果证明了本文所述电流预测控制方法的正确性和实用性。

∶

［1］CASADEID，PROFUMOF，SERRAG，etal.FOCandDTC∶two viableschemesforinductionmotorstorquecontrol［J］.IEEE TransactionsonPowerElectronics，2002，17（5）∶779-787.

［2］SANTANADES，BIME，AMARALDWC.Apredictivealgorithmforcontrollingspeedandrotorfluxofinductionmotor［J］. IEEETransactionsonIndustrialElectronics，2008，55（12）∶4398 -4407.

［3］DIABAAZ，PANKRATOVVV.Modelpredictivecontrolofvectorcontrolledinductionmotordrive［C］//20127thInternational ForumonStrategicTechnology（IFOST），Tomsk，Russia.2012∶1 -6.

［4］SHANBaoming，ZHANGJing.Modelanewkindofdynamicmatrix algorithmintheprocesscontrol［C］//ISA2009International WorkshoponIntelligentSystemsandApplications，Wuhan，China. 2009∶1-4.

［5］UNCHULM，LEEKY.Anadaptivedynamicmatrixcontrolwith fuzzy-interpolatedstep-responsemodelforadrum-typeboiler-turbinesystem［J］.IEEETransactionsonEnergyConversion，2011，26（2）∶393-401.

［6］RODRIGUEZP，DUMURD.Generalizedpredictivecontrolrobustificationunderfrequencyandtime-domainconstraints［J］.IEEE TransactionsonControlSystemsTechnology，2005，13（4）∶577 -587.

［7］ZHANGL，NORMANR.Long-rangepredictivecontrolofcurrent regulatedPWMforinductionmotordrivesusingthesynchronous referenceframe［J］.IEEETransactionsonControlSystemsTechnology，1997，5（1）∶119-126.

［8］LINSHIX，MORELF，LLORAM，etal.Implementationofhybrid controlformotordrives［J］.IEEETransactionsonIndustrialElectronics，2007，54（4）∶1946-1952.

［9］MORELF，LINSHIX，RETIFJM，etal.Acomparativestudyof predictivecurrentcontrolschemesforapermanentmagnetsynchronousmachinedrive［J］.IEEETransactionsonIndustrialElectronics，2009，56（7）∶2715-2728.

［10］何凤有，王从刚，曹晓冬，等.感应电机准无差拍模型预测电流控制策略［J］.电机与控制学报，2013，17（9）∶57-62. HEFengyou，WANGConggang，CAOXiaodong，etal.Quasideadbeatmodepredictivecurrentcontrolstrategyforinduction motordrives［J］.ElectricMachinesandControl，2013，17（9）∶57-62.

［11］齐昕，周晓敏，马祥华，等.感应电机预测控制改进算法［J］电机与控制学报，2013，17（3）∶62-69. QIXin，ZHOUXiaomin，MAXianghua，etal.Improvedpredictivecontrolalgorithmforinductionmotors［J］.ElectricMachines andControl，2013，17（3）∶62-69.

［12］高丽媛，卢达，赵光宙，等.应用自动微分的永磁同步电机预测控制［J］电机与控制学报，2012，16（10）∶38-43. GAOLiyuan，LUDa，ZHAOGuangzhou，etal.Currentcontrol forPMSMbasedonmodelpredictivecontrolwithautomaticdifferentiation［J］.ElectricMachinesandControl，2012，16（10）∶38 -43.

［13］CIRRINCIONEM，PUCCIM.AnMRAS-basedsensorlesshighperformanceinductionmotordrivewithapredictiveadaptive model［J］.IEEETransactionsonIndustrialElectronics，2005，52（2）∶532-551.

［14］SCOLTOCKJ，GEYERT，MADAWALAUK.Acomparisonof modelpredictivecontrolschemesforMVinductionmotordrives ［J］.IEEETransactionsonIndustrialInformatics，2013，9（2）∶909-919.

［15］WIPASURAMONTONP，ZHUZQ，HOWED.Predictivecurrent controlwithcurrent-errorcorrectionforPMbrushlessACdrives ［J］.IEEETransonIndustrialApplications，2006，42（4）∶1071 -1079.

［16］牛里，杨明，刘可述，等.永磁同步电机电流预测控制算法［J］.中国电机工程学报，2012，32（6）∶131-137. NIULi，YANGMing，LIUKeshu，etal.Apredictivecurrent controlschemeforpermanentmagnetsynchronousmotors［J］. ProceedingsoftheCSEE，2012，32（6）∶131-137.

［17］王伟华，肖曦.永磁同步电机高动态响应电流控制方法研究［J］.中国电机工程学报，2013，33（21）∶117-123. WANGWeihua，XIAOXi.Acurrentcontrolmethodforpermanentmagnetsynchronousmotorswithhighdynamicperformance ［J］.ProceedingsoftheCSEE，2013，33（21）∶117-123.

［18］王伟华，肖曦.基于电感辨识的PMSM电流自适应增量预测控制［J］.电机与控制学报，2014，18（2）∶75-82. WANGWeihua，XIAOXi.AdaptiveincrementalpredictivecontrolmethodforcurrentofPMSMbasedononlineidentificationof inductance［J］.ProceedingsoftheCSEE，2014，18（2）∶75 -82.

（编辑∶张诗阁）

Staticcurrenterroreliminationalgorithmforinductionmotor predictivecurrentcontrol

JINXin-hai1，ZHANGYang2，YANGMing1，XUDian-guo1
（1.DepartmentofElectricalEngineering，HarbinInstituteofTechnology，Harbin150001，China；2.ShanghaiSigrinerSTEPElectricCo，.Ltd，Shanghai201801，China）

∶Currentpredictivecontrolofinductionmotorcaneffectivelyavoidthedeteriorationofcontrol performancecausedbydelayincurrentloop，anddynamicperformanceofcurrentcanbeimproved. However，duetomeasurementerror，parameterchangesandotherreasons，deviationprobablyexistedbetweentheinductionmotormodelparameterswhichpredictivecontrollerusedandtheactualmotorparameters，thenstaticcurrenterrorwerecaused，systemefficiencywaslowered，failedtooutputnominal torque，andcouldnotoperateintorquecontrolmode.Basedoninductionmotormodel，influenceoncurrentcontrolstabilitywasquantitativelyanalyzedcausedbypredictivecontrolmodelparametererror，the mathematicalrelationofmodelparametererrorandtheactualfeedbackcurrentstaticerrorwaspresented，andanalgorithmwasproposedtoeliminatethestaticerror.Thealgorithmcorrectedpredictivecontrol modelparametersthroughd、qaxiscurrentfeedback，andstaticerrorcausedbythecontrollermotormodelparametererrorswaseliminated.Withexperimentalresult，thestabilityandeffectivenessofthisproposedmethodwereproved.

∶predictivecurrentcontrol；inductionmotor；parametercorrection；currenterrorelimination

∶TM921

∶A

∶1007-449X（2015）11-0001-09

∶2015-03-02

∶“十二五”国家科技支撑计划项目（2014BAF08B05）

∶金辛海（1974—），男，博士研究生，研究方向为变频器驱动系统，智能控制；

张 扬（1984—），男，硕士，研究方向为变频器驱动系统、交流伺服系统和智能控制；

杨 明（1978—），男，博士，副教授，研究方向为电力电子技术及应用、交流伺服系统和智能控制应用；

徐殿国（1960—），男，教授，博士生导师，研究方向为交流伺服系统、机器人控制技术、风力发电和光伏发电技术等。通讯作者∶张 扬

DOI∶10.15938/j.emc.2015.11.001