并联混合型有源电力滤波器中无源滤波器设计与优化

王玲玲，周 贺，陈辉明，王正仕

（浙江大学电气工程学院，杭州310027）

并联混合型有源电力滤波器中无源滤波器设计与优化

王玲玲，周 贺，陈辉明，王正仕

（浙江大学电气工程学院，杭州310027）

介绍了一种针对中等功率非线性设备网侧谐波补偿的分布式并联混合型有源电力滤波器，并对其中无源滤波器的优化设计问题进行了重点研究，提出了一种实用的无源滤波器优化设计方法；详细分析了无源滤波器参数对有源模块开关管耐压、滤波支路电流的影响并推导了时域解析表达式；基于此优化设计方法，针对整流性负载进行了滤波器参数设计，相比传统的经验设计方法，在相同有源容量情况下，采用新的优化方法设计无源参数，滤波器滤波效果明显改善。仿真及实验结果验证了优化设计方法的有效性。

混合型；有源电力滤波器；无源滤波器；优化设计

引言

电力谐波是工业现代化的主要副产品之一，日益严重的谐波污染对配电系统造成了严重危害，因此电力滤波技术得到了广泛研究。无源电力滤波器PPF（passive power filter），结构简单，但滤波效果易受系统影响；有源滤波器APF（active power filter）滤波效果好，但设备本身成本高、可靠性差［1］。目前，滤波主要是针对系统级别网络，可靠性及可替换性较差，随着变频器等大容量电力电子负载的普及，设备级高性能滤波器的研究具有极其重要的意义。

设备级电力滤波装置要求体积容量小、成本低、补偿效果好且不会对被补偿设备造成严重影响，混合型有源电力滤波器HAPF（hybrid active power filter）有效兼顾了成本和性能，是设备级高性能滤波装置的首选。HAPF的滤波效果及其体积成本在很大程度上依赖于其中PPF的设计［2］。文献［3-5］提出了几种不同的优化设计算法，算法复杂，且都只是针对PPF本身进行研究，忽略了PPF与APF间的相互影响；文献［6］针对HAPF提出了基于神经网络算法的优化方法，其优化目标为减小APF的容量；文献［7］将针对PPF的粒子群优化算法移植到HAPF的设计中。

已有文献提出的PPF优化设计方法，都是将其抽象为规划问题，再应用纯计算机算法进行数值求解，整个过程缺乏对电气关系的定量分析和优化，且算法复杂，缺乏工程实用性。本文在重点考虑PPF与APF之间相互影响的基础上，推导出了重要电气参数关系的解析表达式，对单体设备级HAPF中PPF的参数进行了详细分析并提出了优化设计方法。

1 系统结构分析

设备级滤波器的作用在于滤除设备本身主要次谐波，结构如图1所示，选用二极管整流负载为补偿对象。图中：us、is为电网电压、电流，iL为负载电流，Ls为电网等效电感，ZP为无源滤波器阻抗，负载为谐波源。

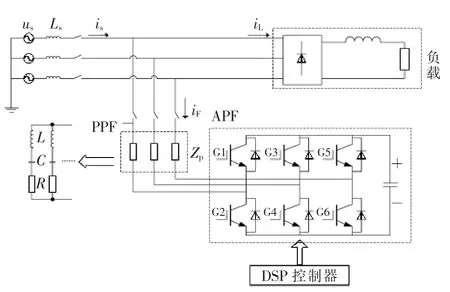
图1 并联混合型有源电力滤波器系统结构Fig.1 System configuration of HAPF

HAPF由APF与PPF直接串联后并入电网。PPF由用于滤除主要次谐波的单调谐滤波器组成，其在APF开关频率处呈高阻抗，能够起到滤除APF输出开关纹波的作用，此外，单调谐滤波器在基波频率处呈现容性，可承受大部分基波电压，从而降低了对变换器直流侧电容和开关器件的耐压等级要求，系统结构简单，成本低，效率高［8］。

本文将APF控制为受控电压源，等效电路如图2所示。其输出电压的参考值V*AF为电网谐波电流ish的K倍，即V*AF=Kish，忽略电网谐波电压，可得系统谐波等效电路如图2（a），分析可得电网谐波电流ish为

式中：ZPh、Zsh分别为PPF阻抗和电网谐波阻抗；iLh为负载谐波电流。APF的作用相当于在电网上串联电阻RK，取值为K，强迫谐波电流流入滤波装置，同时还起到了阻尼Zs和ZP谐振的作用，如图2（b）所示。K越大滤波效果越好，但K不能取太大，否则会影响系统稳定性，因此滤波效果不能完全依赖于K值的选取，还需要对Zp进行优化设计，并且无源参数也会对APF容量、器件应力产生影响。

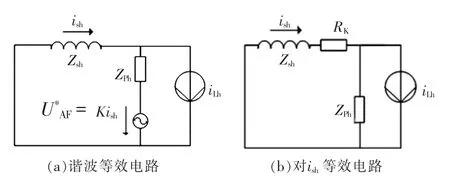
图2 系统谐波等效电路Fig.2 Equivalent circuits for harmonics of HAPF

2 无源滤波器优化设计

2.1 无源滤波器拓扑选择

组成PPF的单调谐支路越多滤波效果越好，但系统复杂性和体积成本会大大提高，因此，在设备级HAPF实际应用中，以单条和两条支路方案为主，具体选择要权衡其滤波能力和成本体积各方面。

二极管整流负载，主要为5、7次谐波。经验设计中，单支路通常将谐振频率设计在7次谐波附近［8-9］；双支路谐振频率通常分别设计在5、7次谐波附近。考虑相同无功补偿能力，设计参数如表1所示，阻抗特性如图3所示。由图3可见，双支路拓扑中的5次谐波阻抗约为单支路的1/2，7次谐波阻抗相差不大，在更高谐波频率处，单支路阻抗小于双支路阻抗。变换器直流侧电压足够高时，通过闭环调节APF谐波阻抗，两种方案均能实现很好的补偿效果。

表1 经验PPF参数Tab.1 Parameters of PPF

图3 PPF阻抗特性Fig.3 Impedance characteristic of PPF

HAPF的成本主要由两部分构成：PPF中的电感电容和APF中的开关管。开关管的成本由其电压电流应力决定，由于APF是一个单端口网络，输入输出分频共用同一端口，因此对其电压电流应进行时域分析。以100 kW负载为例，仅考虑主要次谐波，APF端口电流和电压时域曲线如图4所示。由于设计无功补偿能力相同，APF端口电流基本相同，但电压差别较大，单、双支路所需端口电压峰值分别为43.3 V和34.1 V。由此可见，在相同的端口电流下，双支路比单支路开关管电压应力小；在相同电压应力条件下，双支路方案的电流应力小于单支路。目前开关管价格主要由电流决定，因此，双支路方案APF成本低。但对于PPF部分，双支路方案成本体积必然高于单支路方案。因此，应用中应根据具体情况核算成本并考虑体积要求来选择，本文针对单支路进行参数优化设计。

图4 APF端口电流和电压曲线Fig.4 Current and voltage curves of APF

2.2 PPF参数优化

由式（1）可知，相同K值下，ZPh越小滤波效果越好，其值还会直接影响有源部分电压电流，从而间接影响系统体积及成本。单调谐滤波器电感、电容、电阻值分别为LP，CP，RP，影响其阻抗特性的主要为电感电容。电感电容相同时，RP越小阻抗越小，但RP的微小区别，对滤波效果影响并不大。因此，实际中可结合体积要求，考虑散热问题，估计RP限值，确保设计满足限值要求。以下分析均基于一个假定的RP限值，对LP、CP进行分析设计。单调谐滤波器谐振频率ω与品质因数Q分别为

对LP、CP的设计即为对Q、ω的设计。在分析其选值对电路其他参数影响时，假定系统完全补偿，同时由于APF开关频率限制，接下来的优化设计只考虑主要次谐波。

2.2.1 ω和Q对开关管电压应力的影响分析

PPF在n次谐波频率处的阻抗ZP，n为

式中，ω1为基波频率。故忽略系统谐波电压时，APF输出端谐波电压uAup为

式中φ为阻抗角。因此，开关管电压应力Udc为

利用mathcad可得关系曲线，如图5所示。图5（a）为LC谐振频率对Udc的影响。ω不变时，Udc随着Q的增大而增大；Q不变时，Udc在ω的可行区间内存在最小值。由图5（b）可见，Udc在（ω，Q）的可行域内存在最小值，全域最小值点为最小Q值下的ω最小值点。由此可知，为了减小Udc，需要尽可能减小Q值，并找到最小值点处的ω。

图5 开关管电压应力与ω、Q的关系曲线Fig.5 Relationships between maximum voltage of power switches and ω,Q

2.2.2 ω和Q对滤波支路电流的影响分析

本系统滤波支路电流If包括基波和谐波电流，其时域表达式为

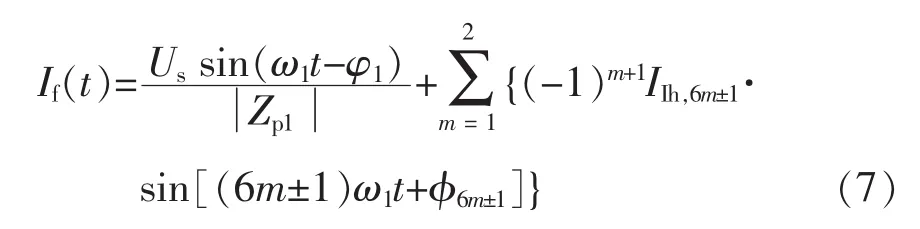
则滤波支路电流峰值If_pk为

利用mathcad计算工具，可得LC谐振频率对滤波支路电流的影响曲线，如图6所示。图6（a）中，当ω不变时，If_pk随着Q的增大而减小；Q不变时，If_pk随着ω的增大而减小。由图 6（b）可见，If_pk在（ω，Q）的可行域内存在最小值，全域最小值点在ω和Q的最大值处。由此可知，为了减小If_pk需要尽可能增大Q值和ω值。

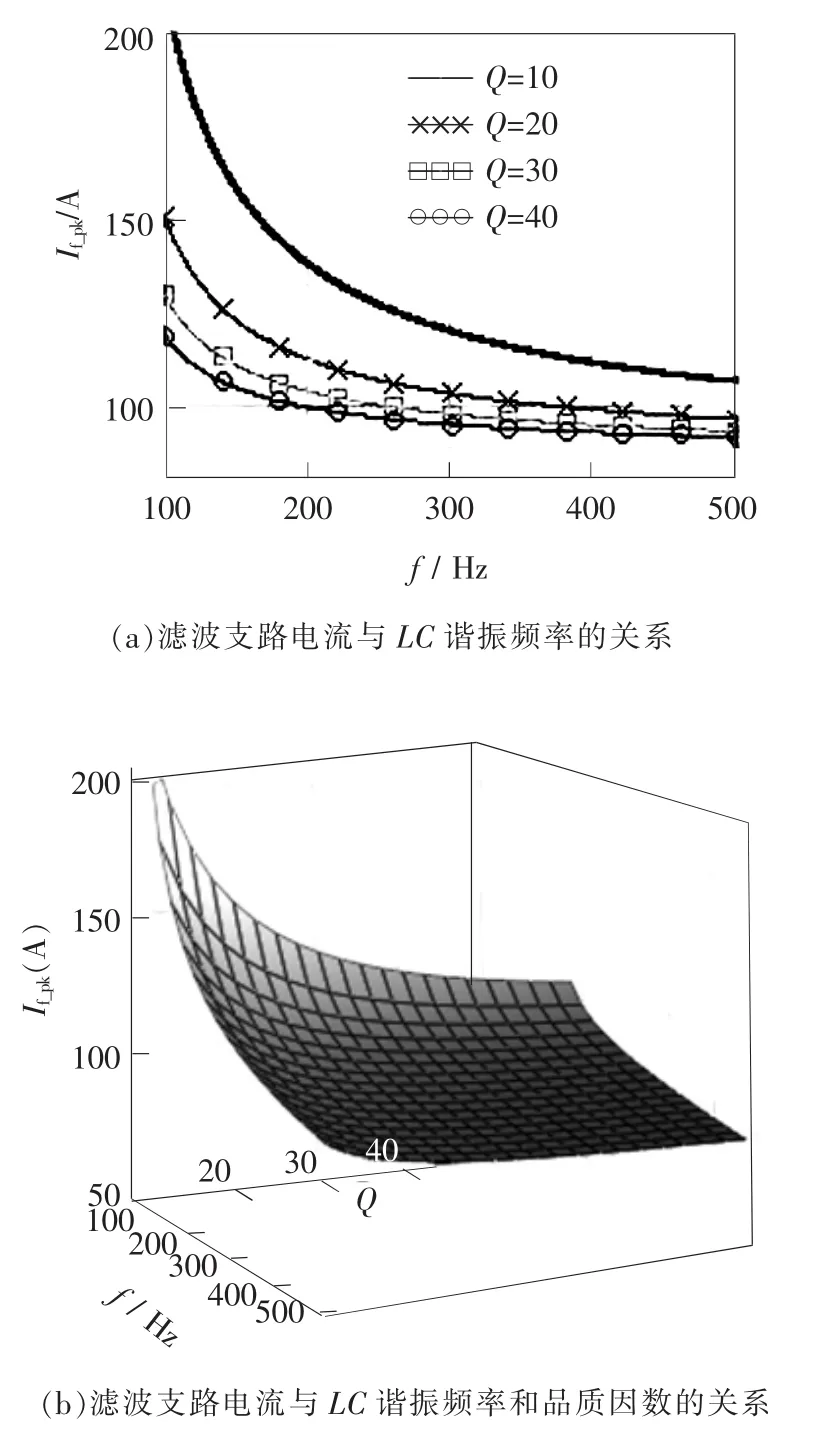
图6 滤波支路电流与ω、Q的关系曲线Fig.6 Relationships between filter branch current and ω,Q

2.2.3 ω和Q的优化设计

由以上分析可知，If_pk与Udc对Q的要求相反，但本补偿装置的目的在于补偿主要次谐波，只辅助提供少量无功，在相同补偿效果时，影响补偿支路电流大小的为基波电流的大小。而实际应用中，受无功补偿容量与系统体积成本限制，基波电流的大小存在限制，即Q值不能太小；随着Q值每增大10，滤波支路电流变化较小，但开关管电压需求约有200 V的升高，故Q值不能太大。因此，可将基波电流峰值ip1_pk选为限制条件Ip1_lim，用以限制Q值，将开关管电压应力Udc作为优化目标，从而得到最优设计结果，具体优化方程为

3 仿真与实验

为验证以上设计，对此HAPF进行仿真和实验，结构如图1所示。主要参数为：电网线电压幅值380 V，频率50 Hz；负载容量100 kW；变换器直流侧电容为2 200 μF；PPF经验参数为：电感2.3 mH，电容100 μF，电阻0.25 Ω，优化参数为：电感1.55 mH，电容184 μF，电阻0.15 Ω。

图7为负载电流iLa及相同APF直流侧电压条件下采用经验参数的网侧电流istra和采用优化参数网测电流isopt的仿真波形，表2为各电流的总谐波畸变率THD（total harmonic distortion）和各次谐波含量（以基波电流为基准）。由表2可知，采用优化参数对5次谐波电流的滤波效果有较大改善，并且网侧电流THD比采用经验参数降低了2.1%，提高了总体滤波效果。

图7 不同THD参数下iLa，istra，isopt仿真电流Fig.7 Simulation waveforms of iLa，istraand isoptwith different THD

表2 负载及电网电流的THD及各次谐波含量Tab.2 THD of load and grid current and harmonics of esimulation %

搭建10 kVA实验系统，其实验波形如图8所示。为提高工作可靠性，IGBT驱动采用了退饱和检测及过流保护技术。由图可见，在相同APF直流侧电压条件下，采用经验PPF参数，网侧电流THD由补偿前28.86%降至8.85%，采用优化PPF参数，THD进一步降至5.34%,实验结果与理论分析和仿真结果相符，验证了本文优化方法的可行性。

图8 不同THD参数下iLa、istra、isopt实验波形Fig.8 Experimental waveforms of iLa，istraand isoptwith different THD

4 结语

本文介绍了一种由PPF和APF直接串联构成的并联混合型有源电力滤波器，并分析了其工作原理，利用时域分析方法推导出了PPF参数对有源部分的影响，提出了一种实用的PPF参数的优化设计方法。通过Matlab仿真和10 kVA实验系统验证了该优化方法的有效性，表明：在相同APF直流侧电压条件下，优化的PPF参数能够有效提高HAPF的谐波补偿性能；在保证相同补偿效果时，优化的参数可降低有源部分的容量。

［1］王兆安,杨君,刘进军.谐波抑制与无功功率补偿［M］.第2版.北京:机械工业出版社,2002.Wang Zhaoan,Yang Jun,LIU Jinjun.Harmonics suppression and reactive power compensation［M］.Second edition.Bejing:China Machine Press,2002（in Chinese）.

［2］Shuai Zhikang,Luo An,Zhu Wenji,et al.Study on a novel hybrid active power filter applied to a high-voltage grid［J］.IEEE Trans on Power Delivery,2009,24（4）:2344-2352.

［3］Y M Chen.Passive filter design using genetic algorithms［J］.IEEE Trans.Power Syst.,2003,50（1）:202-207.

［4］Y P Chang,C J Wu.Optimal multiobjective planning of largescale passive harmonic filters using hybrid differential evolution method considering parameter and loading uncertainty［J］.IEEE Trans.Power Del.,2005,20（1）:408-416.

［5］Huang Lina,He Na,Xu Dianguo.Optimal design for passive power filters in hybrid power filter based on particle swarm optimization［C］.Proceedings of the IEEE International Conference on Automation and Logistics,Jinan, 2007:1468-1472.

［6］B Duro,V S Ramsden,P Muttik.Minimization of active filter rating in high power hybrid filter system［C］.Proc.IEEE Int.Conf.Power Electron Drive Syst.,Hong Kong, 1991:1043-1048.

［7］He Na,Xu Dian Guo,Huang L.The application of particle swarm optimization to passive and hybrid active power filter design［J］.IEEE Trans on Industrial Electronics,2009,56（8）:2841-2851.

［8］时晓洁，王智强，张军明，等.单调谐并联混合有源电力滤波器控制策略研究［J］.电机与控制学报，2012,16（4）: 64-71.Shi Xiaojie,Wang Zhiqiang,Zhang Junming,et al.Study on the control strategy for single-tuned hybrid active power filters［J］.Electric Machines and Control,2012,16（4）:64-71（in Chinese）.

［9］Srianthumrong S,Akagi H.A medium-voltage tansformerless AC/DC power conversion system consisting of a diode rectifier and a shunt hybrid filter［C］.Industry Applications Conference,2002:78-85.

Design and Optimization of Passive Power Filter in Shunt Hybrid Active Power Filter

WANG Lingling,ZHOU He,CHEN Huiming,WANG Zhengshi
（College of Electrical Engineering,Zhejiang University,Hangzhou 310027,China）

This paper presents a distributed shunt hybrid active power filter for medium-power nonlinear devices’net harmonic current compensation.Research on the optimization of passive power filter is made and a practical design method is proposed.The effects of passive filter parameters on the switch voltage pressure and current of compensation approach are analyzed and the time domain analytical expressions are got.Based on this optimization method,passive filter parameters are designed for rectifier load system.Compared to traditional empirical design method,new optimization method improves the effect of filter significantly.Simulation and experimental results demonstrate the effectiveness of this optimization method.

hybrid;active power filter;passive power filter;optimization

王玲玲

王玲玲（1990-），女，硕士研究生，研究方向：有源电能质量控制技术，E-mail：wanglljs@163.com；

周贺（1991-），男，硕士研究生，研究方向：有源电能质量控制技术、高性能DC-DC变换器，E-mail：zhouhejl@163.com；

陈辉明（1963-）通信作者，男，博士，教授，研究方向：高频感应加热、半导体技术、电力电子在节能与新能源中的应用，E-mail：huiming@zju.edu.cn；

王正仕（1965-），男，博士，副教授，研究方向：高性能开关电源、逆变功率电源、电力电子在节能与新能源中的应用，E-mail：wzs@zju.edu.cn。

10.13234/j.issn.2095-2805.2015.2.52

：TM 402

：A

2014-11-13

863计划资助项目（2012AA053601）

Project Supported by 863 Plan（2012AA053601）