基于航天测控通信系统LT码的应用研究

缪鹏飞，周 帅，姜洪伟，卫 芬

（1.上海航天技术研究院，上海 201109；2.北京理工大学 信息与电子学院，北京 100081；3.上海空间电源研究所，上海 200245）

0 引言

航天测控通信系统中由于信号传输距离遥远，接收信噪比较低，这必然增加了通信过程出现数据差错的概率。信道编译码技术有较高的编码增益，可提高信号接收能力，成为了保证信息可靠传输的有效手段之一［1］。目前，广泛用于航天测控通信系统中的信道编译码主要是Turbo码和LDPC码，两者均具备逼近Shannon极限的优异译码性能，CCSDS已提出了航天任务中的相关标准［2－3］。最新的VSAT卫星系统及火星科学实验号等航天任务即分别采用了Turbo乘积码和LDPC码作为差错控制技术，为用户提供可靠的数据通信服务。Turbo译码存在译码复杂度较高，且只能适于传输数据率较低场合等缺点［4］。LDPC码因编码矩阵的构造对其应用造成了一定的限制。

LUBY在1998年首次提出了泉技术［5］。随着数字喷泉码的快速发展，喷泉码（LT码和Raptor码）在航天测控通信系统中应用的优势逐渐显现。喷泉码是一种非固定码率的编码，发送端可发送任意数量的数据包，而无需反馈信道，简化了通信协议中的握手过程，缩短了传输时延。同时其译码过程采用了简单的模二和运算，编译码计算复杂度低，具有良好的可扩展性和对异质用户支持，利于未来航天通信网的构建和运行，且影响喷泉码译码性能只有数据包数量和编码构造，这样利于抵抗复杂的航天测控通信电磁环境中可能引起的突发性错误。

目前，喷泉码研究工作焦点主要是地面站Internet网及无线通信，在航天测控通信系统中的应用研究较少，后者需要喷泉编译码具备更优的编译码性能［6］。文献［7］研究了深空通信中的喷泉编译码技术，但重点是喷泉编码和通信协议的结合以减少重传过程，缩短传输时延，并未对误码率需求进行分析。文献［8］基于数字喷泉编码也仅对中继信道的功率分配进行了研究。文献［9－10］虽然从通信可靠性角度研究了LT－LDPC，LT－RS等编译码级联方案，但未给出具体的理论分析，也没有对其进行适应性优化。

本文以LT码为研究对象，针对航天测控通信应用背景，对一种适用的LT编译码方案进行了研究。

1 LT编译码原理

LT码作为一种通用的喷泉码，是第一类码率不受限码。LT码的度分布定义为一个输出数据节点的度为d的概率ρ（d），编码算法步骤如图1所示。

图1 LT编码过程Fig.1 LT encoding

a）取一个度分布，根据度分布选取编码数据包的度数d；

b）从待编码数据的数据包中随机地选取d个；

c）将这d个数据包进行模二和运算，生成编码数据包。

d）选择不同的d，重复步骤a）～c），可得编码数据包t2，t3，…，tn。

LT码的编码可用分组码生成矩阵的方法表述。令x为示输入符号集，vi为第i个编码符号系数向量，定义LT码生成矩阵

则LT编码就是由输入符号集根据编码生成矩阵GLT进行线性运算的过程，即

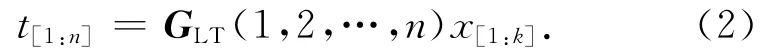
式中：k，n分别为待编码和编码后数据数。

对LT码的译码来说，若可重构Tanner图，即译码器知道给定的输出编码是由何不同原始输入数据异或而得的，则当译码器接收到K个（K常略大于k）输出数据就能译码。LT码的译码如图2所示。其中：顶层节点和底层节点分别对应原始数据包和编码数据包。

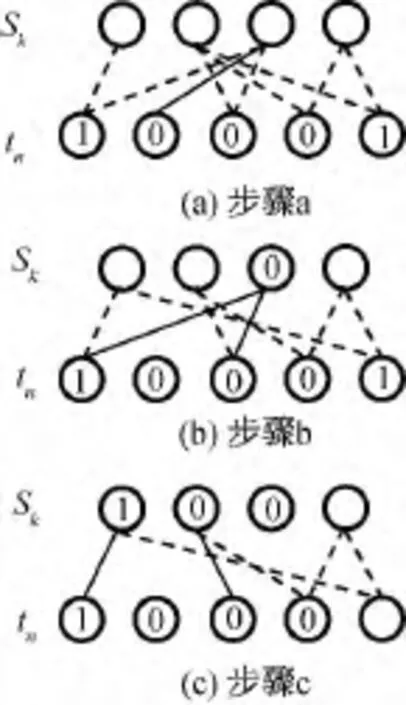
图2 LT码译码Fig.2 LT decoding

a）在接收到的编码数据包中找到度值为1的数据包，即某一个连接数为1的tn，如无此数据包，继续接收直至找到为止，如图2（a）所示。

b）由tn可得与其相连的原始输入数据Sk，即Sk＝tn，如图2（b）所示。

c）对应与Sk连接的其他数据包与其异或，将Sk与编码数据包间的连接线删除，相当于对数据包进行更新，对应度值减1，即ti＝Sk⊕ti，i≠n，如图2（c）所示。

d）重复步骤a）～c）直至全部Sk得以恢复，则译码成功；否则，译码失败，须接收更多的编码数据包才能继续译码。

实际上，LT码的译码过程为式（2）的反过程，即有

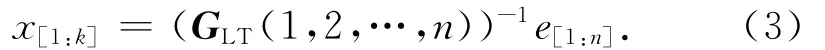
式中：e［1：n］为经信道传输受噪声干扰的编码数据包。只要矩阵G满秩，式（3）就能计算。

2 度分布函数分析与优化

航天测控通信系统需具备良好的译码性能，而度分布函数是影响译码性能的关键，因此，构造一好的度分布函数对LT码有重要的意义。

2.1 最优度分布理论模型

由前文分析可知，最优度分布函数一方面要求尽量少的编码数据包数，这样能通过m个（m略大于k）编码数据包覆盖所有的输入原始数据分组，减少译码开销，另一方面又要求尽量小的编码数据包平均度数，这样可降低生成每个编码数据包所需的运算量，降低编译码代价。

本文对最优度分布函数进行理论推导。由文献［11］可得编码数据包释放概率

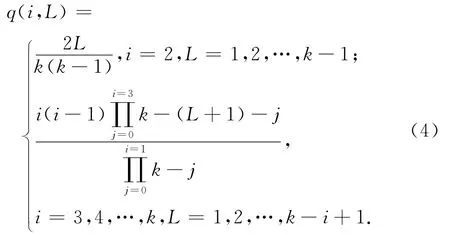
式中：q（i，L）为在还有L个原始数据包未处理的条件下，度为i的编码数据包释放概率。当i＝1时，有q（i，k）＝1。

编码数据包总释放概率r（i，L）表示度为i的编码数据包在还有L个原始数据分组未处理时选中同时释放概率，即r（i，L）＝ρ（i）q（i，L）。r（L）表示某一编码数据包在L个原始数据包未处理时释放的概率，有

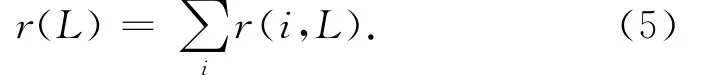
给出预处理集的定义，译码过程中对所有度为1的编码数据包进行释放，恢复出其对应的原始数据包，称被恢复出但还未被处理的原始数据包集合为预处理集。

设预处理集中原始数据分组为R＋1个，如有L个原始数据分组未被处理，为保证预处理集中原始数据分组个数不变，处理完第k－L个原始数据分组后，须添加一个新的原始数据分组到预处理集之中。一个被释放编码数据包所对应原始数据分组不落在原有预处理集概率为（L－R）／L，为保证增加一个新的原始数据分组到预处理集中，需平均释放编码数据包个数

因在还有L个原始数据分组未被处理，一个编码数据包被释放的概率

因此，当编码数据包总数为E时，则第k－L步处理后平均释放编码数据包个数

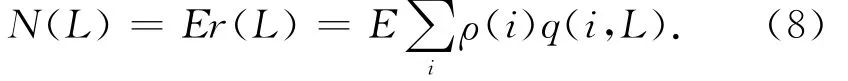
由M（L）＝N（L）可得

综合式（4）、（9），有

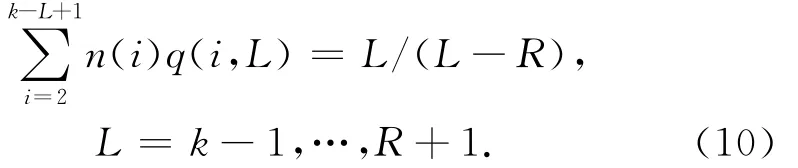
式中：n（i）＝Eρ（i）；E（（1）＋n（2）＋…＋n（k－R）＝E。由式（4）可求得系数矩阵。令ρ（1）＝（R＋1）／k，以保证预处理集的初始大小为R＋1，由式（10）可得最优分布函数

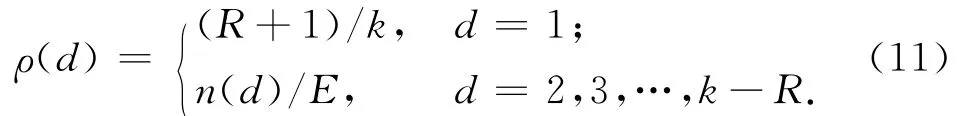
实际应用中，当原始数据分组数k较大时，系数矩阵对角线上大部分元素趋于0，造成运算量急剧增加，变量ρ（i）很难被求出，严重限制了具体应用。因ρ表示一个度分布函数中度数为i的概率，若不能确定ρ（i）的表达式，则LT编码时就不能获知编码结果来自何待编码数据模二和，这限制了其应用。

2.2 混合型度分布函数

目前，实际应用的度分布主要有鲁棒孤立子分布和二进制指数分布，其中鲁棒孤立子分布是在理想孤立子分布中引入参数c，δ［12－13］。对c，δ赋予合适的值，使译码过程中度为1的编码数据包期望个数约为

式中：δ为译码中未恢复全部原始数据包的概率；c为介于0到1之间的常数。

给出函数定义

然后，τ与理想孤子分布ρ相加，即

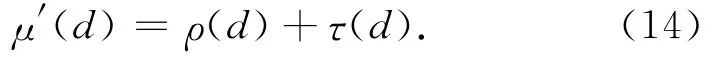
归一化鲁棒孤子分布后可得

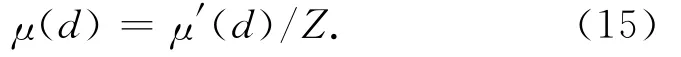
二进制指数分布通过增加较小度数的概率，可缓解上述不足，分布表达式为

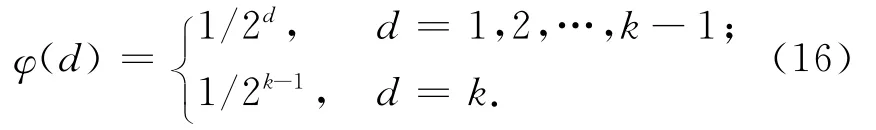
式中：d为各编码数据包的度；k为编码时原始数据包数食粮；φ（d）为二进制指数分布条件下编码数据包中度为d的概率。

基于上述分析，本文采用将鲁棒孤立子分布和二进制指数分布这两种度分布函数组合的方法，给出一种LT编码混合型度分布函数

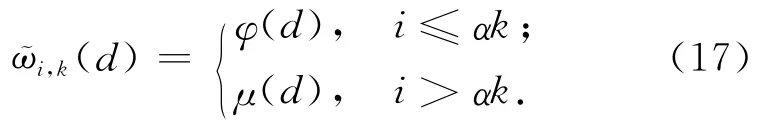
3 性能仿真

3.1 概率分布

对鲁棒孤立子分布和二进制指数分布的概率分布进行仿真分析。设源数据长度k＝100，常数c＝0.1，译码失败概率δ＝0.2，则s＝6，k／s＝16。两种分布的概率如图3所示。

由两种分布的概率可知：鲁棒孤立子分布中d为2的值所占比例较低，而d为16的值所占比例较高，这是为了实现原始数据分组的良好覆盖，但可能会存在译码中断问题；二进制指数分布中概率较高的区域主要集中于编码度值d＜9的范围内，这样小编码度值的大量存在可有效保证译码的顺利进行，但由于覆盖度问题，同时也会产生一定的译码冗余度。

与单一度分布函数不同，采用本文提出的混合型度分布函数的LT编码器的前k个喷泉编码数据包的度服从φ（d），保证初始阶段译码器接收到充足的度很小的编码数据包，便于启动译码，而此后的喷泉编码数据包的度服从μ（d），主要是为减少冗余数据的传输，提高译码效率。

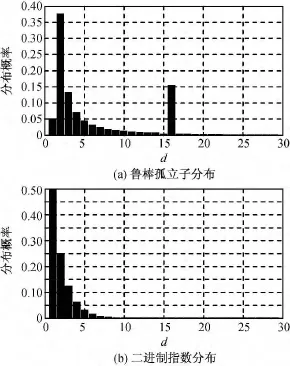
图3 鲁棒孤立子分布及二进制指数分布概率Fig.3 Robust solution and binary exponential distribution

3.2 分割点确定

分割点值α对混合型度分布函数有重要影响。分析基于蒙特卡洛仿真α的取值，取值依据是在源数据包被全部恢复的条件下译码器接收到的编码数据包最少时的α值。

设α的取值步长为0.05，且每个源数据包数量为k条件下，编码器发送的编码数据包的数量由50次蒙特卡洛仿真的平均值求得。源数据包全部被恢复条件下，k分别为300，400，500时对应的发送编码数据包数量。其中：鲁棒孤立子分布中的c＝0.05，δ＝0.1。

由图4可知：当α＝0时，对应的是鲁棒孤立子分布下编码器发送的编码数据包数量；随着α取值的增大，编码器发送的编码数据包数有先降低后增加的趋势，当且仅当α＝0.1时编码器发送的编码数据包数量为最少，由仿真归纳可得此值为最佳分割点。

3.3 译码性能

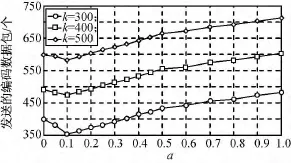
图4 编码器发送编码数据包数Fig.4 Code data under variousα

对LT码的译码效率和误码率性能进行仿真分析。在k＝1 000时，采用3种不同的度分布进行LT编码，译码器成功译码的源数据包的比率与正确接收的编码数据包的数量间的关系如图5所示［14］。

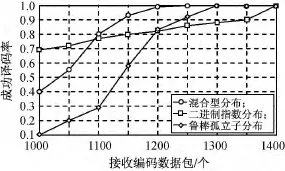
图5 成功译码比率与接收的编码数据包关系Fig.5 Relation between encoded data and decoding ratio

混合型度分布与鲁棒孤立子分布相比，当译码器正确接收到的编码数据包较少时，对应的译码器成功译出的源数据包比率更大，即译码器能译出更多的源数据包。虽然与二进制指数分布相比，在接收到较少编码数据包时，译码器成功译码的源数据包的比率较低，但随着接收到编码数据包数的增加，其比率值上升更快，译码效率提高了（1 400－1 200）／1 200＝16.67%。

将改进后的LT码用于文献［15］提出的适于航天测控通信系统中的LT－LDPC级联码方案中，分析误码率，结果如图6所示。

由图6可知：译码器误码率为达到10－5时，Turbo码、LT－LDPC级联码与RS卷积级联码需要的信噪比分别高于0.53，1.31，1.60dB。LT－LDPC级联码的译码性能优于RS卷积级联码，虽略低于Turbo码约0.78dB，但其性能仍能满足一般航天测控通信系统的需求，同时远小于Turbo码的计算复杂度利于实现设计。

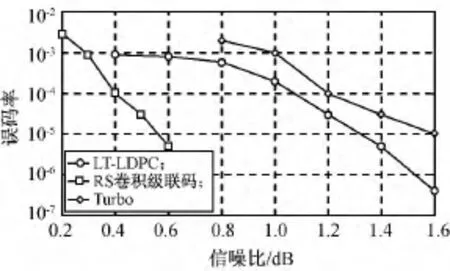
图6 LT－LDPC码RS卷积级联码及Turbo码误码率Fig.6 BER of LT－LDPC，RS－Convolution and Turbo

4 结束语

本文以航天测控通信为研究背景，对一种适用的LT编译码方案进行了研究。采用新的混合型度分布函数，有效提高了译码效率，在接收到同样多的正确喷泉码数据包后可译出更多的原始数据。蒙特卡洛仿真和系统性能分析结果表明：在航天测控通信条件下，改进后的LT码与LDPC码级联方式不仅具备了接近于Turbo码的优异译码性能，并且编译码计算复杂度低，利于星载平台的实现，满足系统应用需求。

［1］ 杨友福，刘建伟，张其善，等.卫星信道编码技术及新发展［J］.通信学报，2008，41（7）：30－36.

［2］ LI L，ROBERT G M，BASHIR M A，etal.A lowcomplexity Turbo decoder architecture for energy－efficient wireless sensor networks［J］.IEEE Transactions on Very Large Scale Integration System，2013，21（1）：14－22.

［3］ UENG Y L，YANG B J，YANG C J，etal.An efficient multi－standard LDPC decoder design using hardware－friendly shuffled decoding［J］.IEEE Transactions on Circuits and Systems，2013，60（3）：743－755.

［4］ WONG C C，CHANG H C.High－efficiency processing schedule for parallel Turbo decoders using QPP interleaver［J］.IEEE Transactions on Circuits and Systems，2011，58（6）：1412－1420.

［5］ KENTA K，DAVID D，KOHICHI S.Fountain coding via multiplicatively repeated non－binary LDPC codes［J］.IEEE Transactions on Communications，2012，60（8）：2077－2083.

［6］ LEE S K，LIU Y C，CHIU H L，etal.Fountain codes with PAPR constraint for multicast communications［J］.IEEE Transactions on Broadcasting，2011，57（2）：319－325.

［7］ 李 晖，姚文顶，张乃通.深空通信中的喷泉编译码技术［J］.电讯技术，2008，4（48）：8－12.

［8］ CAO R，YANG L Q.Decomposed LT codes for cooperative relay communications［J］.IEEE Journal on Selected Areas in Communications，2012，30（2）：407－414.

［9］ 姚文顶，李 晖，陈立甲，等.深空通信中喷泉码技术研究［J］.系统工程与电子技术，200，31（1）：40－44.

［10］ WANG Z，LUO J.Fountain communication using concatenated codes［J］.IEEE Transacions on Communications，2013，61（2）：443－454.

［11］ 朱宏鹏，张更新，谢智东.喷泉码中LT码的次优度分布［J］.应用科学学报，2009，27（1）：6－11.

［12］ PANG K，LIN Z H，BARTOLOMEU FU，etal.Distributed network coding for wireless sensor networks based on rateless LT codes［J］.IEEE Wireless Communications Letters，2012，1（6）：561－564.

［13］ ANYA A，CLAIRE G，KATIA J R，etal.Toward increasing packet diversity for relaying LT fountain codes in wireless sensor networks［J］.IEEE Communications Letters，2011，15（1）：52－54.

［14］ SHAO H Q，XU D Z，ZHANG X F.Asymptotic analysis and optimization for generalized distributed fountain codes［J］.IEEE Communications Letters，2013，17（5）：988－991.

［15］ 焦 健，张钦宇，李安国.面向深空通信的喷泉编码技术［J］.宇航学报，2010，31（4）：1156－1161.