一类基于改进的当前统计模型的目标跟踪算法研究

戚 靖，刘成成，郭伟龙，蔡云泽

（1.贵州航天天马机电科技有限公司，贵州 遵义 563003；2.上海交通大学 系统控制与信息处理教育部重点实验室，上海 200240）

0 引言

近些年来，对目标跟踪已经进行了深入研究，尤其是对广泛用于军用和民用领域的机动目标跟踪技术，提出了多种不同算法。一般，两类不确定问题影响了目标跟踪的性能，一是目标机动性的难以确定，另一是量测来源难以确定。对机动目标模型的研究，就是关于目标机动不确定性的研究。

与传统模型相比，通过充分考虑之前的运动状态和环境影响，“当前”统计模型已能较好地适应过程噪声［1］。特别是与之前的Singer模型相比，“当前”统计模型能更准确地描述目标机动强度的调整和范围的变化，是较好的实用跟踪模型。虽然“当前”统计模型的应用在一定程度上提高了目标跟踪算法的精确性和运行性能，但该模型存在局限性和缺点。模型中引入了参数机动频率，传统的“当前”统计模型将其取为常值，不能实时自适应调整［2］。显然这与实际目标运动不相符，且目标机动时滤波误差会不可避免地增大。为此，本文对一种在线调整方法进行了研究，分析Singer，CS模型后提出了一种改进的匀速运动模型，以提高目标在弱机动时的跟踪精度。

1 当前统计模型及其改进

“当前”统计模型是一种非零均值时间相关模型。它假设目标加速度a（t）满足

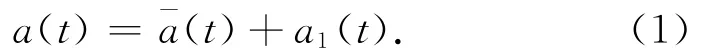
式中；（t）为当前时刻加速度的均值；a1（t）为零均值的一阶马尔可夫过程，且

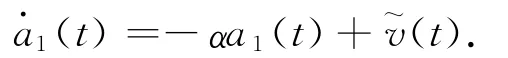
此处：α为机动频率；（t）为零均值的高斯白噪声。由此可得连续时间下目标加速度满足

将式（3）离散化，可得“当前”统计模型的一维离散状态方程为

U（k）为输入控制阵，且

此处：α为参数机动频率；T为采样周期。设（k）在每个采样周期内不变，且“当前”时刻加速度均值为前一个时刻加速度的估值X（k＋1｜k）。

对均值为零的离散时间白噪声序列（t），噪声序列方差

式中：q11，q12，…，q33以机动频率和采样周期为参数；（σk）2为机动目标的加速度的方差，且

由式（6）～（8）可知：“当前”统计模型的自适应性表现在依据机动目标的当前时刻的加速度，对机动加速度方差进行调整，从而自适应调整状态估计噪声协方差阵。进一步分析，可将“当前”统计模型理解为过程噪声方差自适应调整的匀加速度模型［3］。

当跟踪两维、三维运动目标时，只需对公式进行扩维即可。

对雷达、红外等非线性观测方程，在目标的跟踪和状态滤波估计中，广泛采用扩展卡尔曼滤波算法，滤波方程为

很明显，当T以及观测噪声方差R（k）确定后，自适应调整的过程噪声方差对滤波结果有重要影响。由式（8）、（10）可知：其取值与α和最大正负机动加速度有关系。典型的“当前”统计模型将这两个参数取为常值，在滤波过程中不作自适应调整。因为机械特性，实际目标在机动过程中加速度存在极限值，故将最大加速度取值为常数在一定程度上是符合实际的，但目标在机动过程中，机动特性不可能始终不变，因此将机动频率取值为常数并不符合实际，需要改进算法对其进行自适应调整。

定义新息变量

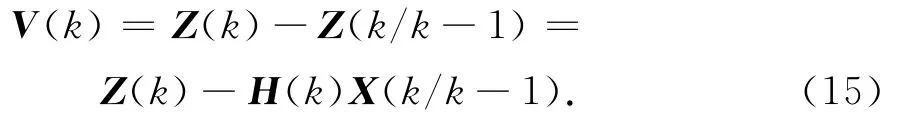
新息即是观测值与预测观测值的残差。根据机动目标统计特性可知，新息向量服从正态分布，即

式中：σ2，u分别为新息向量的方差和均值。令

观测值到预测观测值的马氏距离

定义统计距离

注1：当机动发生时，原机动频率将不再适用，应进行调整，且D将发生较大变化。因此，可根据D的变化判断机动的发生。

已证明机动检测算法有时延的缺点，自适应调整机动频率具有一定的实际意义。因为D的取值与新息的协方差C有关，因此可将式（19）定义的统计距离用于机动频率的自适应调整。

设初始机动频率α＝α0，自适应调整机动频率的策略为

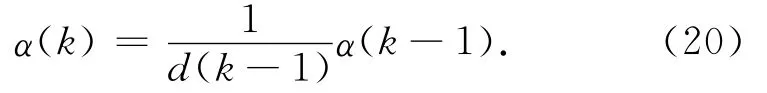
2 匀速模型及其改进

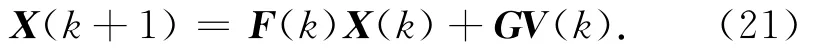
3 基于改进CV、CS的交互式多模型算法

传统算法中，基于实际工程考虑，会采用不同的跟踪模型，每种模型对应一种运动状态。但每个时刻仅有一个模型作用，根据观测数据与滤波结果间的统计分析，实现不同滤波模型的转换。

模型切换是机动目标跟踪中的难点。变维滤波等传统算法多以硬切换为主，即使用不同的跟踪模型，以对应运动状态变化的机动目标。显然，这将不可避免地造成一定滞后。交互式多模型（IMM）算法采用一种基于软切换的机制，有效克服了传统方法中硬切换缺点［6］。

交互式多模型方法中，滤波器根据目标不断变化的运动状态，应用相应的跟踪模型，通过计算模型概率，构造估计状态的线性组合，实现各子模型滤波器交互作用。各模型间以一个马尔可夫链为基准进行模式变换。该算法通过各模型滤波器间的输入输出交互，将获得各模型估计值合并后的加权估计作为综合估计，是一种十分有效的多模型算法。

设整个过程存在r个跟踪模型

式中：Wj（k）为高斯白噪声序列；j＝1，…，r。由马尔可夫链可达到对所有模型软切换的协调控制，马尔科夫转移矩阵

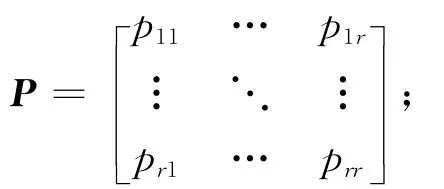
测量模型为

IMM算法步骤可归纳如下。

a）输入交互

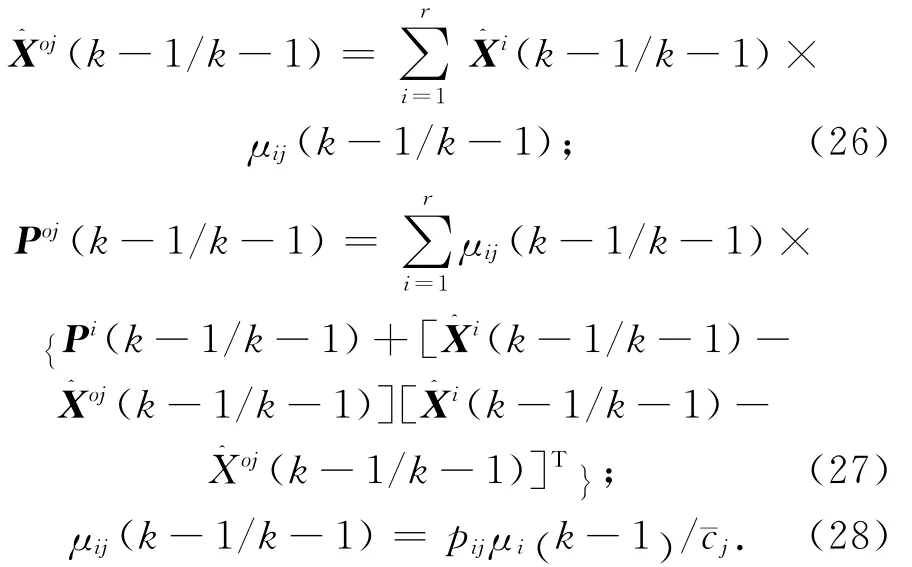
式中：pij为模型i转至模型j的转移概率；为归一化常数，且

b）模型条件滤波

对应本文，分别采用改进的CV，CS两个滤波模型。

c）模型概率更新

此处：

d）输出交互

4 仿真

为检验本文设计的CV－IACAM－EKF算法的有效性，用Monte Carlo仿真进行检验。对实验结果，取相应的方差数据作为评价指标：进行扩展卡尔曼滤波后，机动目标的状态估值和目标运动的实际轨迹最小均方误差。采用本文改进后的速度自适应模型（IACAM）和改进后的匀速模型，通过交互式多模型（IMM）算法组合，与匀速－匀加速模型的EKF滤波算法比较。在进行时空配准后，雷达和红外的采样时间T均为1s，Monte Carlo仿真30次，仿真总步数为60。设目标的模拟轨迹为：初始位置，X向0km，Y向1km处；X向初始速度30m／s，加速度0m／s2，Y向初始速度30m／s，加速度0m／s2。0～30s保持初始状态作匀速运动，30～60s，X向加速度5m／s2，Y向加速度6m／s2，作匀加速直线运动。仿真结果如图1～6所示。

图1 机动目标运动轨迹Fig.1 Motion trajectory of maneuvering target

图2 X向位置跟踪误差Fig.2 Position tracking error in Xdirection

图3 Y向位置跟踪误差Fig.3 Position tracking error in Y direction

由仿真结果可知：本文设计的改进CV－IACAM模型的距离估计和速度估计均优于传统CV－CA模型。在匀速阶段，交互模型中经改进的匀速模型具有对时变噪声的自适应调整的能力，滤波的精度有较大的提高，误差小于同时段的原模型；在匀加速阶段，在自适应加速度模型的调整跟踪中，能较好地识别加速度大小变换或方向变化，以进行跟踪，滤波误差亦低于传统模型。尤其在模型转换时，改进CV模型的跟踪效果优于原模型，显著减小了匀速段的跟踪误差，使机动发生时的误差累积较小，由此模型转换时的跳变也相对减小。

图4 Y向速度跟踪误差Fig.4 Velocity tracking error in Y direction

图5 CV－IACAM模型概率Fig.5 Probability of CV－IACAM model

图6 CV－CA模型概率Fig.6 Probability of CV－CA model

5 结束语

在机动目标的运动轨迹较为复杂时，传统的匀速模型误差累积较大，不能及时矫正，导致匀加速模型工作时的误差累积很大，模型转换时的跳变也较大。本文设计改进的匀速－改进的自适应加速度模型较好地解决了这一问题。通过仿真实验进行了分析和比较，对工程应用有一定的指导意义。本文尚缺少严格的数学推导证明，后续将从理论上对本文方法进行证明。

［1］ 周宏仁，敬忠良，王培德.机动目标跟踪［M］.北京：国防工业出版社，1991.

［2］ 潘 泉.机动目标跟踪双滤波器模型及自适应算法［J］.控制理论与应用，1995，12（4）：482－486.

［3］ 钱华明，陈 亮，满国晶，等.基于“当前”统计模型的机动目标自适应跟踪算法［J］.系统工程与电子技术，2011，33（10）：2154－2158.

［4］ 陈 勇，董永强.基于“当前”统计模型的模糊自适应滤波算法［J］.火力与指挥控制，2010，35（8）：177－179.

［5］ 罗笑冰，王宏强，黎 湘，等.非线性“当前”统计模型及自适应算法［J］.系统工程与电子技术，2008，30（3）：397－403.

［6］ BLOM H A P，BAR－SHALOM Y.The interacting multiple model algorithm for systems with markovian switching coefficients［J］.IEEE Trans Automatic Control，1988，33（8）：790－783.