三相电压型PWM整流器的双滑模控制方案研究

郑宏伟，饶益花，陈文光

（1.南华大学电气工程学院，湖南衡阳 421000；2.南华大学数理学院，湖南衡阳421000）

引言

三相PWM电压型整流器输入电流谐波小、输出电压稳定、能实现单位功率因数运行和能量双向传输，具有很好的工业应用价值。但由于PWM整流器是一个强非线性系统，故采用常规的线性控制方式（如PI调节器）难以达到理想的控制效果，动态性能差且参数调节复杂。滑模控制是解决非线性系统控制问题的重要方法之一，因抗干扰能力强、动态响应速度快等优点受到各国控制研究学会的广泛关注[1]。滑模控制在本质上是一种不连续控制，它要求快速地切换系统的控制状态，具有高频开关特性。这与PWM整流器开关器件工作在高频 “开―关”模式相对应，因此滑模控制很适合应用于PWM整流器系统的控制。

大部分基于滑模控制的三相PWM整流器，电压外环采用滑模控制，电流内环采用非滑模控制的线性或非线性控制方法[2-12]，并采用空间向量脉宽调制（SVPWM）技术对输入信号进行调制以产生开关器件控制脉冲，设计和实现较为复杂，且对系统整体的动态响应速度和鲁棒性造成影响。本文提出电压外环、电流内环均采用滑模控制的双滑模控制方案，以简化设计和实现，并保证整个系统具有良好的鲁棒性和动态性能。运用Matlab中的Simulink和SimPowerSystems搭建了系统仿真模型，对双滑模控制方案和电压外环采用滑模控制、电流内环采用PI控制方案进行对比仿真，结果验证了双滑模控制方案的可行性与优越性。

1 三相电压型PWM整流器数学模型

三相电压型PWM整流器的主电路拓扑结构如图1所示。R和L为交流侧电感等效参数，C为直流侧支撑电容，RL为直流侧负载电阻。 其中，ua、ub、uc为PWM三相控制电压。

假设ea、eb、ec为三相对称交流电源，应用基尔霍夫定理可得三相电压型PWM整流器在三相静止坐标系下的数学模型为

式中，Sa、Sb、Sc分别表示三相桥臂开关管的开关函数。其中：S=1，代表对应的上桥臂开关管导通，下桥臂开关管关断；S=0，代表对应的下桥臂开关管导通，上桥臂开关管关断。通过“等功率”坐标变换，将三相静止坐标系中的变量变换到两相旋转d-q坐标系中，数学模型改为

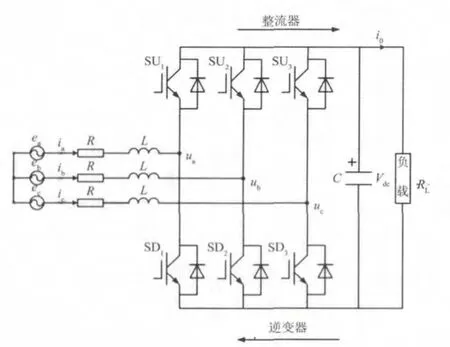
图1 三相电压型PWM整流器的主电路拓扑结构

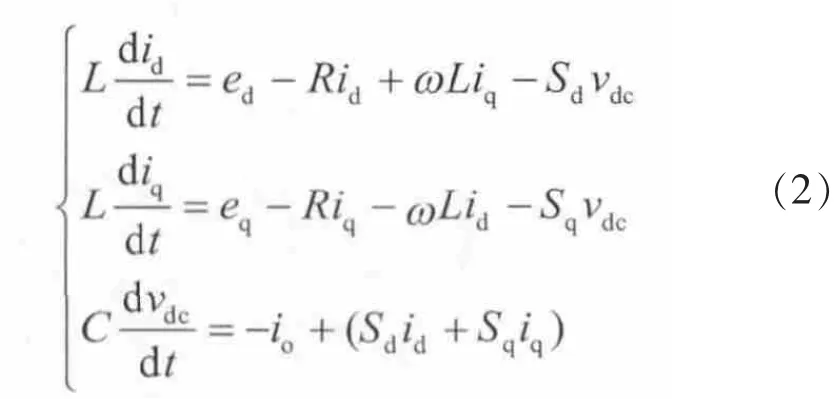
式中：Sd、Sq分别表示三相桥臂开关管在d-q坐标系下的开关函数；ed、eq和id、iq分别为电网侧交流电压和电流的d、q分量；ω为角频率。

2 滑模控制系统的设计

2.1 基于滑模控制的电压外环设计

三相电压型PWM整流器有两个自由度Sd、Sq。其中，Sd用于控制直流侧输出电压vdc；Sq用于控制输入功率因数。对输入功率因数的控制可转换成对输入无功电流iq的控制，当控制iq=0时，PF=1。滑模控制的目标是整流器输入单位功率因数（即输入无功电流跟踪给定无功电流i*q=0）和输出电压vdc跟踪给定电压，属于非线性系统的跟踪问题。根据文献[1-3,13]设计滑模面

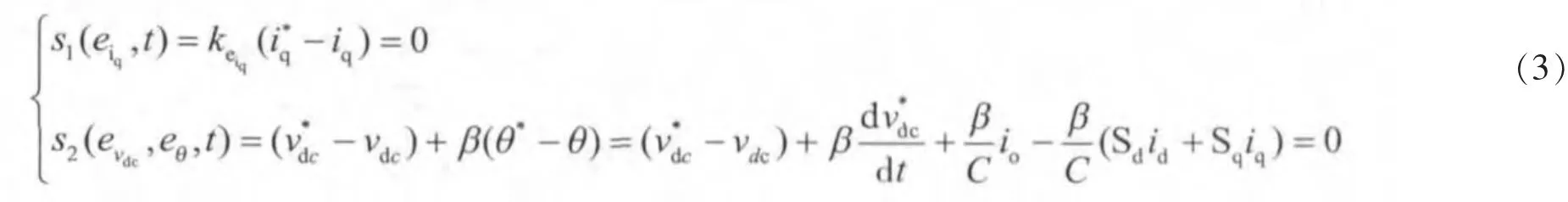
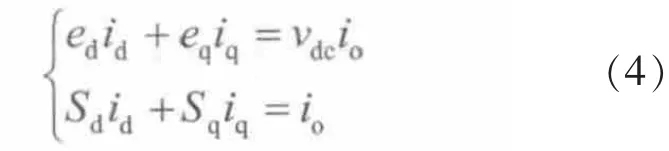
将式（5）代入滑模函数 s2(evdc，eθ，t)得

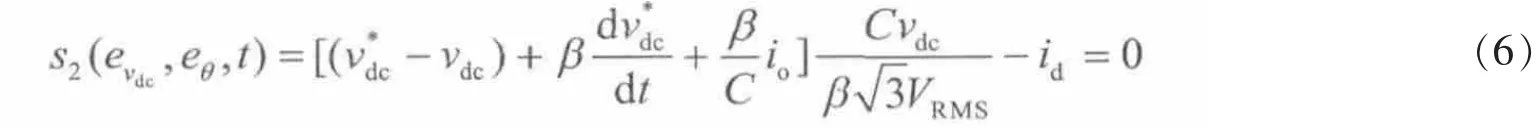
结合式（3）、式（5），得到系统的滑模函数为

其中

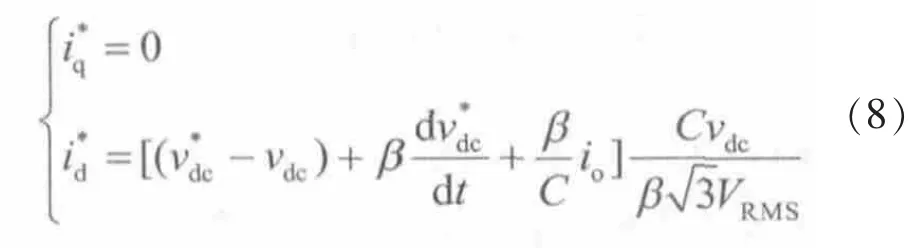
2.2 基于滑模控制的电流内环设计

根据参考文献[14]，可定义电流内环的滑模函数为

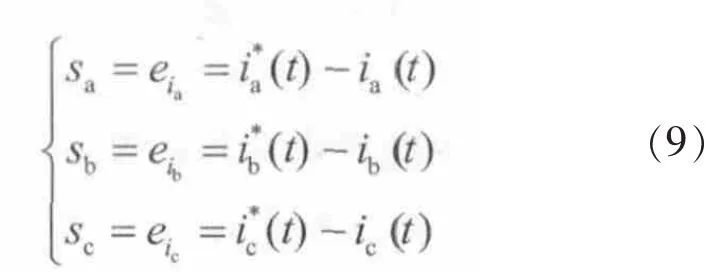
其中，ia、ib、ic为交流侧各相电流；为交流侧各相电流参考值，由电压外环滑模控制得到的通过两相旋转d-q坐标系向三相静止坐标系变换得到；eid、eib、eic为跟踪误差电流。根据滑模控制可达性条件 ss＞0[15]和式（1）、式（9）有

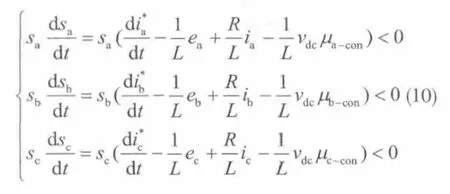
其中，μx-con（x=a,b,c）分别为 a、b、c 三相的控制作用，使所有运动轨迹于有限时间内到达滑模面[16]。

电流内环采用滑模变结构控制的等速趋近律[15]

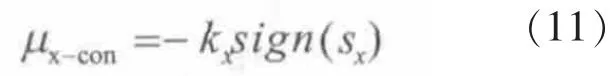
kx为电流环滑模控制系统的设计参数，只需满足

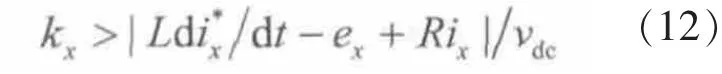
即能保证系统满足滑模控制可达性条件。假设滑模函数满足 sa＜0，sb＜0，sc＞0，由式（1）、式（10）和式（11）得

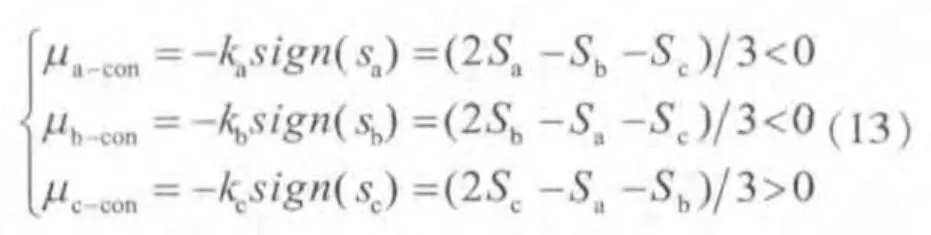
满足以上不等式方程组的开关模式只有（1，1，0）。依此类推，可以得到不同情况的滑模函数组合对应的开关模式，如表1所示。当系统进入滑动模态时，开关可根据需要适当工作在零矢量 （0，0，0）或（1，1，1）模式，以减少开关切换次数。 同时，考虑采用变趋近律的滑模控制方式（如指数趋近律、幂次趋近律[15]），让运动点在离滑模面较远时，采用较大的趋近律，缩短调节时间，提高动态响应速度；在接近离滑模面时,采用较小的趋近律或零趋近律，从而大大降低系统进入滑动模态时开关的切换频率。综合采用上述方法，既可有效减少开关损耗，提高系统工作效率；又可减弱滑模控制系统的“抖振”现象[15]，提高系统的可靠性。

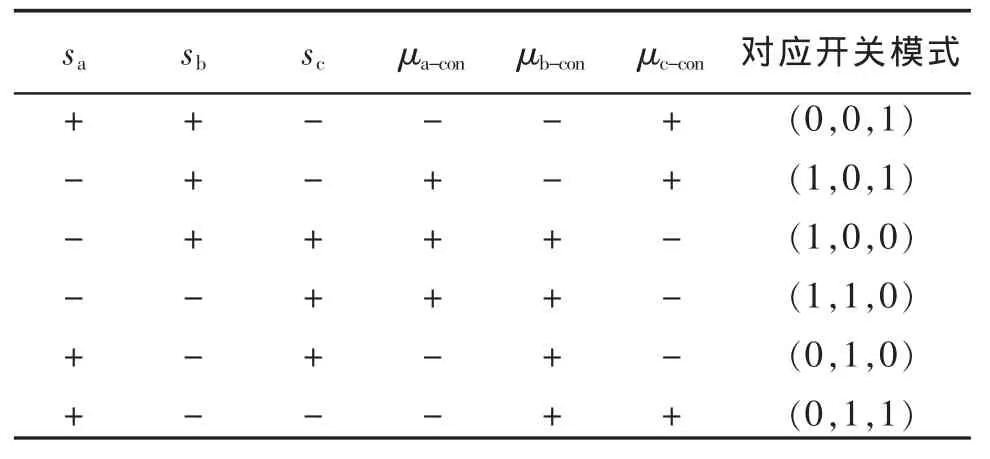
表1 滑模控制规律

3 仿真结果及分析

本文在Matlab/Simulink环境下搭建的三相PWM整流器系统的仿真模型如图2所示。其中，output_voltage_control_loop模块是电压外环控制模块，根据第3.1节设计的滑模控制算法搭建；input_current_control_loop模块是电流内环控制模块，分别采用第3.2节设计的滑模控制算法和PI控制算法搭建，以进行对比仿真。系统整体控制原理图分别如图3、4所示。设计系统主要参数为：直流电压700 V，交流三相电压380 V，功率等级为7.5 kW，开关频率为10 kHz，网侧滤波电感9.5 mH，直流支撑电容1 000 μF，β=0.01。电流内环采用PI控制时，设置kp=500，ki=100。进行仿真并比较、分析仿真结果。

采用双滑模控制时，仿真可得到电流内环滑模函数sa的曲线以及对应的A相上桥臂开关管的控制脉冲，用以分析滑模控制工作原理。由图5、6可知，当t在0.01 s附近时，系统进入滑动模态。此时，滑模函数在滑模面附近作高频运动，对应生成开关器件的高频控制脉冲，按滑模控制规律快速切换开关器件的“开”、“关”状态，从而实现对PWM整流器网侧输入电流以及直流侧输出电压的实时控制。

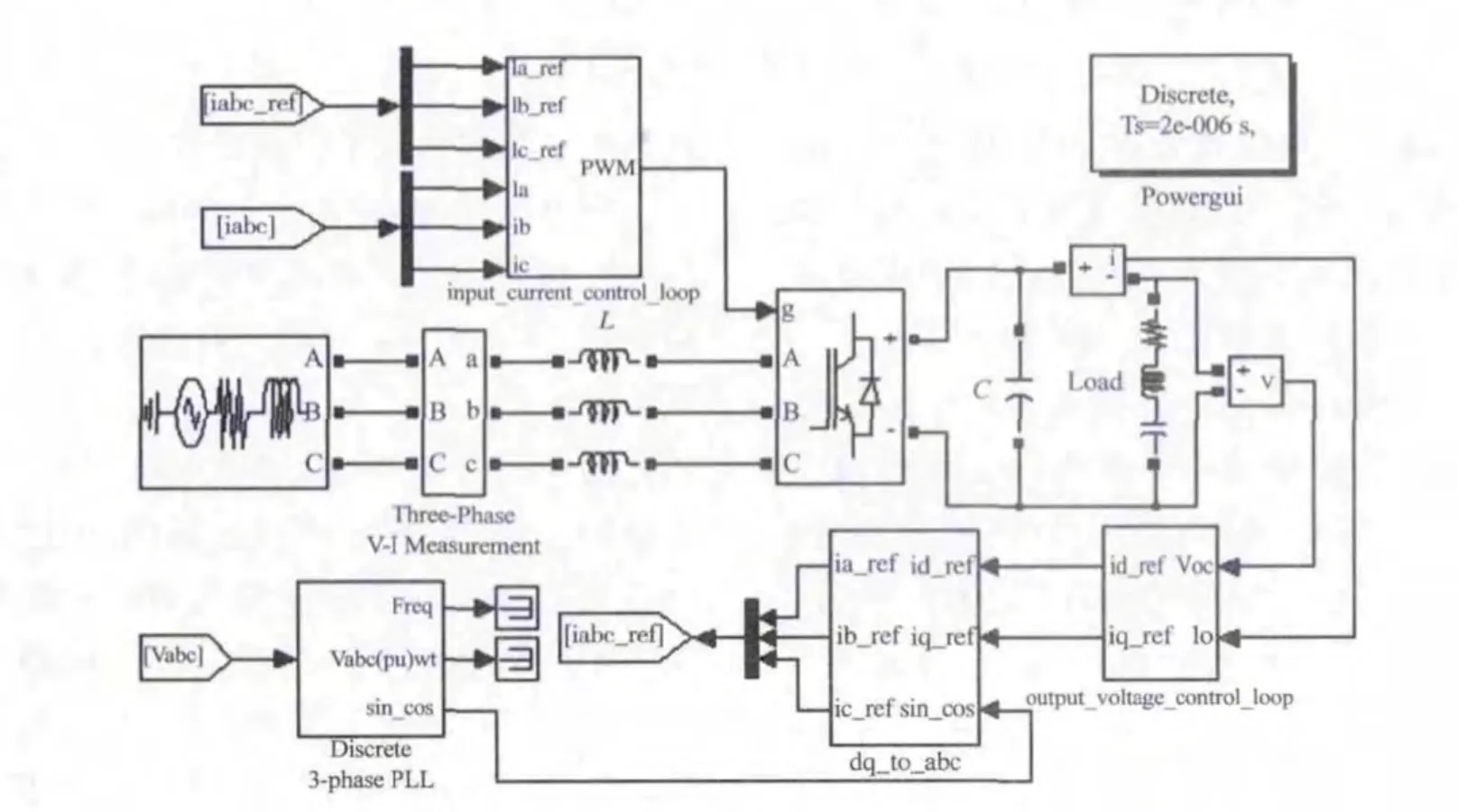
图2 三相电压型PWM整流器系统模型

图3 三相电压型PWM整流器控制原理图（双滑模控制）

图4 三相电压型PWM整流器控制原理图（电流内环采用PI控制）

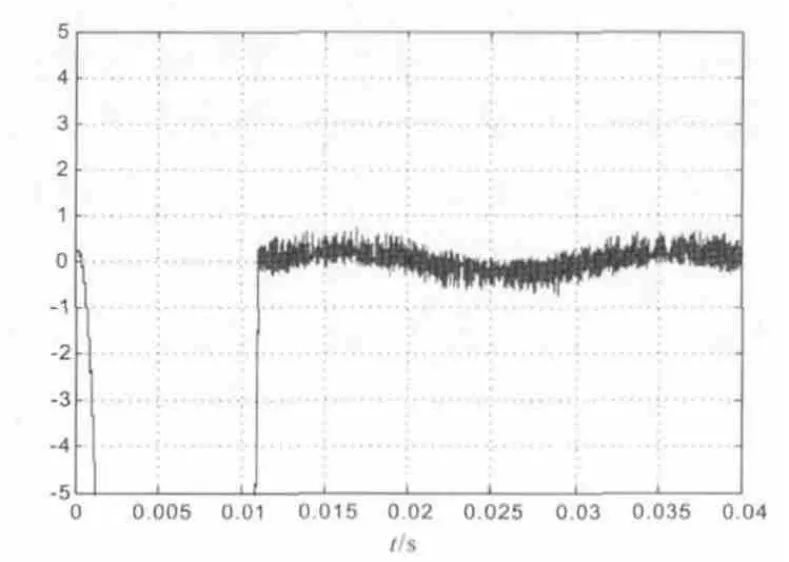
图5 滑模函数sa的曲线

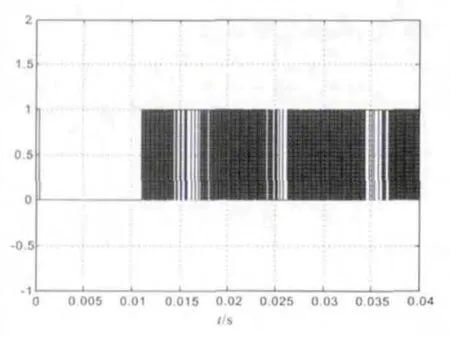
图6 A相上桥臂开关管控制脉冲

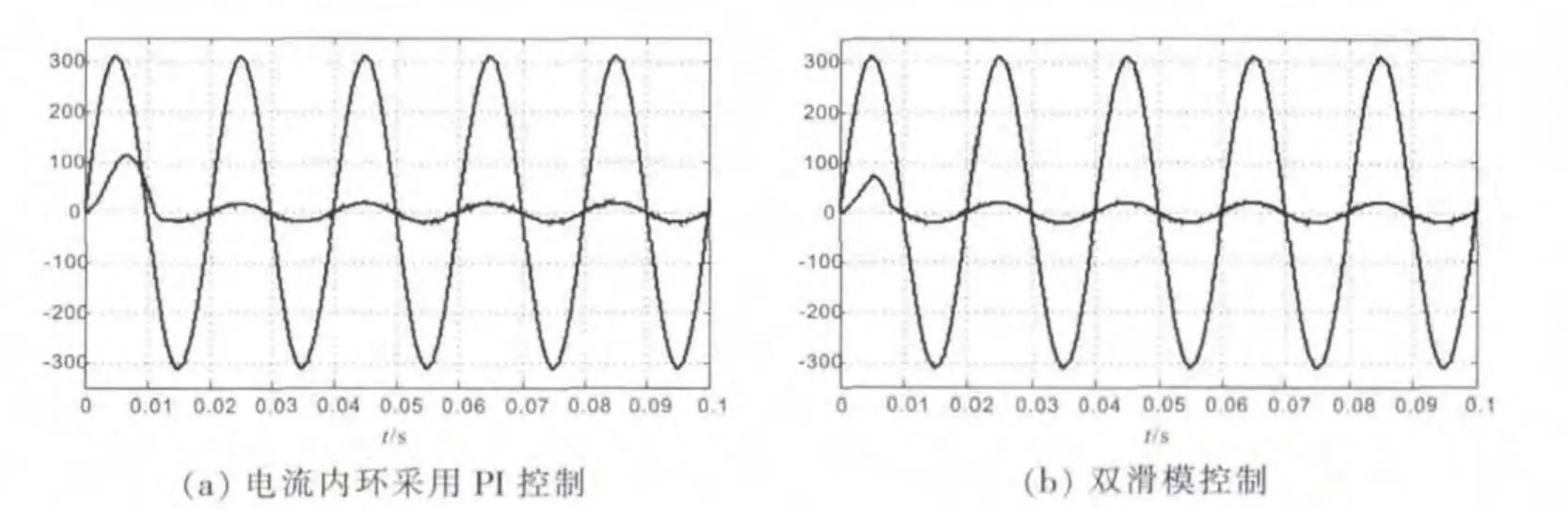
图7 A相电压和电流波形

图7 为A相电压和电流波形。比较图7（a）、（b）可知，采用双滑模控制可提高交流侧电流跟踪电压的速度，降低系统未进入滑动模态时交流侧电流峰值，这对降低开关器件参数要求、节约成本有利。

图8 为A相电流谐波含量分布图。由图7可知，交流侧电流均能够完全跟踪电压，位移因子cosα=1。 由图 8（a）可知，A 相电流总谐波畸变 THD=4.42%，功率因数由图8（b）可知，A相电流总谐波畸变THD=0.67%，功率因数，几乎为 1，实现网侧电流单位功率因数控制。

图9 为直流侧电压动态响应波形。比较图9（a）、（b）可知，采用双滑模控制时，输出电压动态响应快速，在t=0.01 s时已达到稳定状态，无超调量且无稳态误差。

图10 为网侧电压由额定电压变为150%额定电压时直流电压的动态响应波形（t=0.2 s），图11为直流电压指令由700 V变为600 V时直流电压的动态响应波形（t=0.2 s）。比较图 10（a）、（b）和图 11（a）、（b）可知，采用双滑模控制时，直流侧电压波动小，恢复稳定状态所需时间短，证明双滑模控制的PWM整流器系统具有更优越的鲁棒性和动态性能。

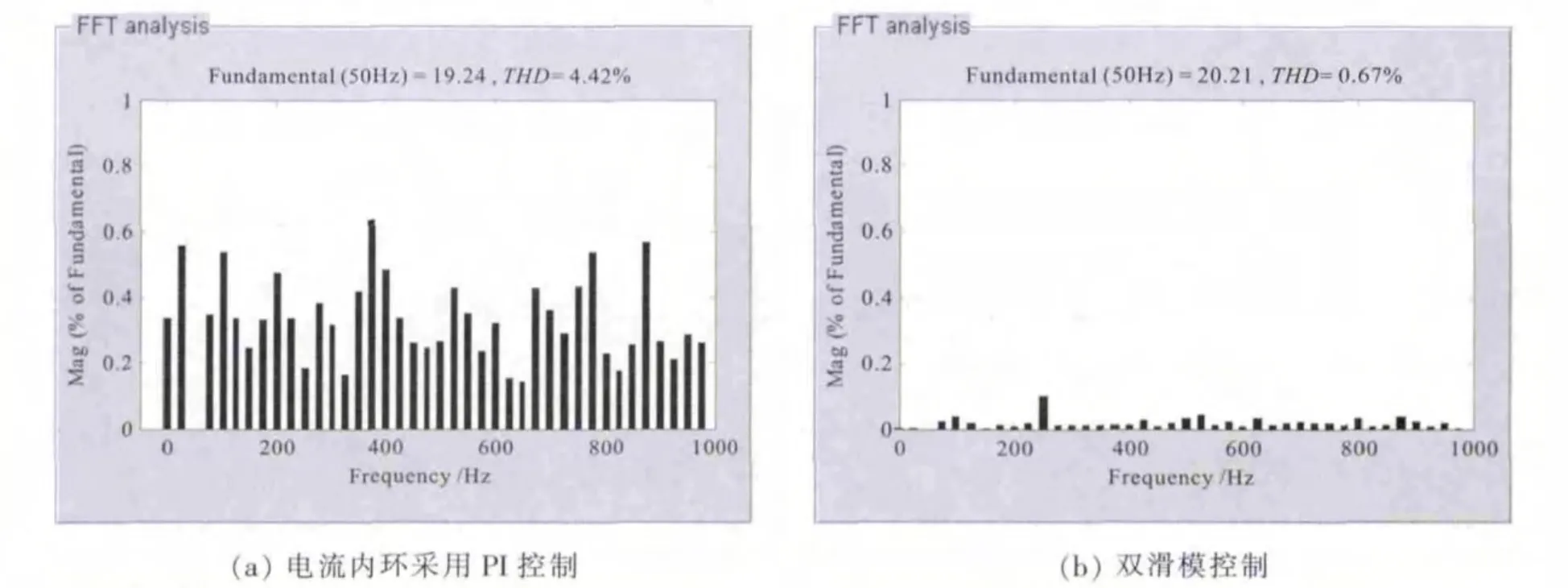
图8 A相电流谐波含量分布图

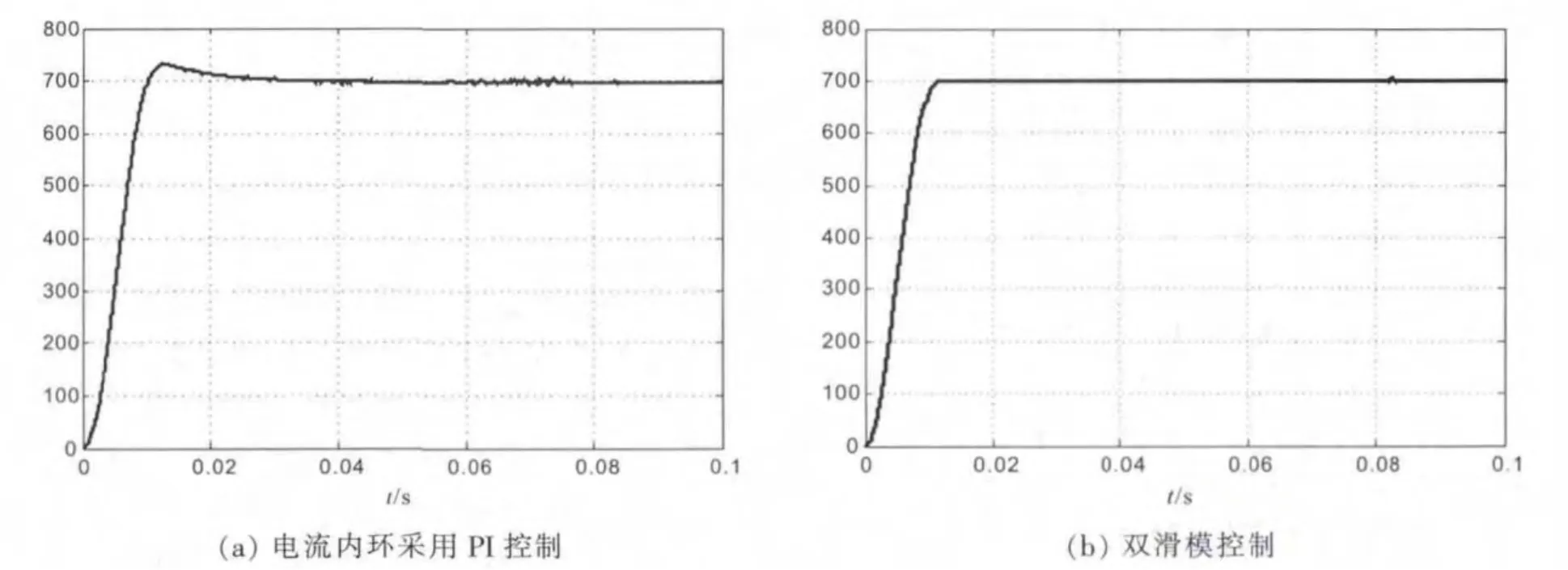
图9 直流侧电压动态响应波形

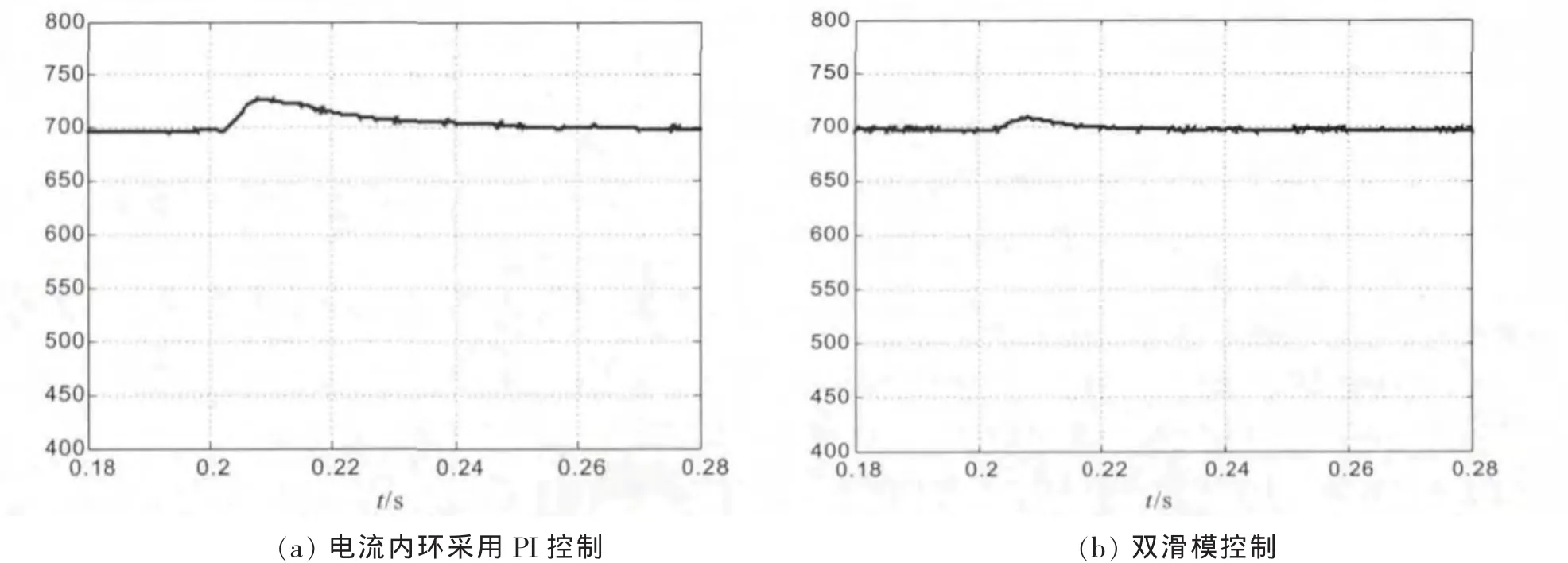
图10 网侧电压由额定电压变为150%额定电压时直流电压的动态响应波形（t=0.2 s）

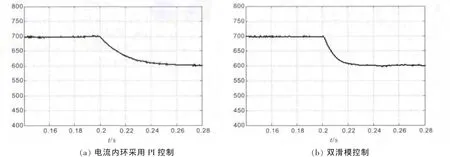
图11 直流电压指令由700 V变为600 V时直流电压的动态响应波形（t=0.2 s）

4 结论

为简化三相电压型PWM整流器的设计和实现，提高整体系统的动态性能和鲁棒性，本文提出了一种电压外环、电流内环均采用滑模控制的双滑模控制方案，并详细介绍了滑模控制系统的设计过程。最后，在Matlab/Simulink中搭建了系统仿真模型，对双滑模控制方案和电压外环采用滑模控制、电流内环采用PI控制方案进行对比仿真。仿真结果验证了双滑模控制方案的可行性与优越性，具有工业应用价值。

[1]Young K D,Utkin V I,Ozguner U.A control engineer's guide to sliding mode control[C].IEEE International Workshop on Variable Structure Systems,1996：1-14.

[2]Silva J F.Sliding mode control of voltage sourced boosttype reversible rectifiers[C].IEEE International Symposium on Industrial Electronics,1997,2：329-334.

[3]Silva J F.Sliding-mode control of boost-type unity-powerfactor PWM rectifiers[J].IEEE Transactions on Industrial Electronics,1999,46(3)：594-603.

[4]Zhang Z,Xie Y,Le J,et al.Decoupled State-Feedback and Sliding-Mode Control for Three-Phase PWM Rectifier[C].Power and Energy Engineering Conference,2009 Asia-Pacific.IEEE,2009：1-5.

[5]Wang W,Yin H,Guan L.A direct power control scheme for three-phase PWM rectifiers based on sliding-mode variable structure control theory[C].IEEE International Conference on Power Electronics and Drive Systems.2009：837-842.

[6]HUANG K,WANG W,WANG X.Modeling and Simulation of PWM Rectifier Based on Sliding-Mode Control[J].Power System Technology,2009,8：005.

[7]Fan W,Bao G.PWM rectifier research based on sliding mode variable structure control[C].Control and Decision Conference,2011 Chinese.IEEE,2011：675-679.

[8]Kim J H,Jou S T,Choi D K,et al.Direct Power Control of Three-Phase Boost Rectifiers Using a Sliding-Mode Scheme[J].Journal of Power Electronics,2012,12(4).

[9]汪万伟,尹华杰,管霖.三相电压型PWM整流器的反馈线性化和滑模控制[J].华南理工大学学报 (自然科学版),2009,37(11)：83-87.

[10]帅定新,谢运祥,王晓刚.三相 PWM整流器混合非线性控制研究[J].中国电机工程学报,2009(12)：30-35.

[11]洪庆祖,谢运祥.基于滑模控制的 PWM整流器的研制[J].电力电子技术,2012,46(1)：35-36.

[12]黄辉先,汤湘宁.基于模糊滑模控制的三相 PWM整流器仿真[J].电源技术,2013,37(005)：836-839.

[13]Silva J F.Sliding Mode Design of Control and Modulator Electronics for Power Converters[J].Journal of Circuits,Systems,and Computers,1995,5(03)：355-371.

[14]周卫平,吴正国,刘大明,等.有源电力滤波器变趋近律滑模变结构控制[J].中国电机工程学报,2005,25(23)：91-94.

[15]高为炳.变结构控制的理论及设计方法[M].北京：科学出版社,1996.

[16]张兴,张崇巍.PWM整流器及其控制[M].北京：机械工业出版社,2003.