新型单周期控制的无桥Boost PFC变换器

温向宇，赵丽平，李健华，吴志坚

（西南交通大学电气工程学院 ，四川 成都 610031）

引言

近年来，一种新的控制方式——单周期控制(OCC)技术[1-2]得到广泛关注，与传统的控制算法相比，单周控制不需要乘法器，采样电路简单且抗干扰能力强。但工作于连续导电模式CCM(Continuous Conduction Mode)的单周控制PFC变换器电感尺寸过大，二极管存在反向恢复问题；工作于断续导电模式DCM(Discontinuous Conduction Mode)的单周控制PFC变换器电流应力大，电磁干扰严重。上述问题限制了系统功率因数进一步的提升。

文中将混合模式HCM (Hybrid Conduction Mode)下的改进型单周控制应用到无桥Boost PFC电路中，很好的解决了二极管反向恢复和电磁干扰(EMI)问题，进一步提高了系统功率因数，同时控制电路设计简单，便于日后工程应用。

1 控制策略及工作原理

工作于HCM下的单周控制方程是在CCM模式和DCM模式控制方程的基础上经过数学推导、整合得到，在此，先需了解CCM和DCM模式的工作原理。

1.1 CCM工作模式

该模式下的控制方程为：

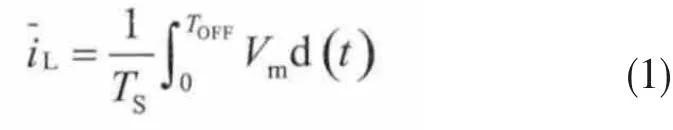
式中：Vm为控制变量Vm=VO/Re；iL为平均输入电流；Re为变换器输入电阻；TS为开关周期。考虑到IG=VG/Re，则：

式中：VO为输出电压；VG为输入电压；IG为输入电流。Vm与输入电流成正比关系，通过电流传感器可以实现对电流的实时检测。

1.2 DCM模式

DCM模式下的基本型控制方程为

d 为占空比；其中

式中：fs为开关频率；L为升压电感。由式(3)可知，该模式控制电路的实现需要借助于电压传感器，这与借助电流传感器实现的CCM模式控制电路是截然不同的，因此，要想实现两种模式的整合，需要对式(3)，即DCM模式的控制方程进行适当的变形[3]。考虑到

将式(4)和(5)带入式(3)得到

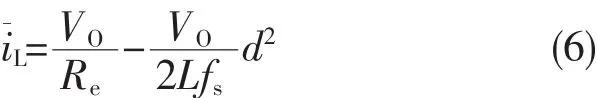
式(6)化简为：

其中，Vm=VO/Re，Vn=VO/(2LfS)=KVVO此时的控制变量Vm和CCM模式下的控制变量完全相同，即此时的Vm与输入电流成正比关系。

DCM模式新的控制方程如式(6)所示。它的主要特点是用电流传感器代替电压传感器实现对控制电路输入的采样，同时为下一步DCM和CCM模式的整合创造了条件。

1.3 HCM模式

（1） 理论依据

由以上分析可知，DCM和CCM模式的控制变量均与输入电流成正比关系，且都需要使用电流传感器，因此便可以整合以上两种工作模式形成全新的HCM模式单周控制策略[4]。该模式包含的两个控制变量Vm相同，因此可以使用相同的输出电压PI控制器。HCM单周控制无桥Boost PFC电路如图1。

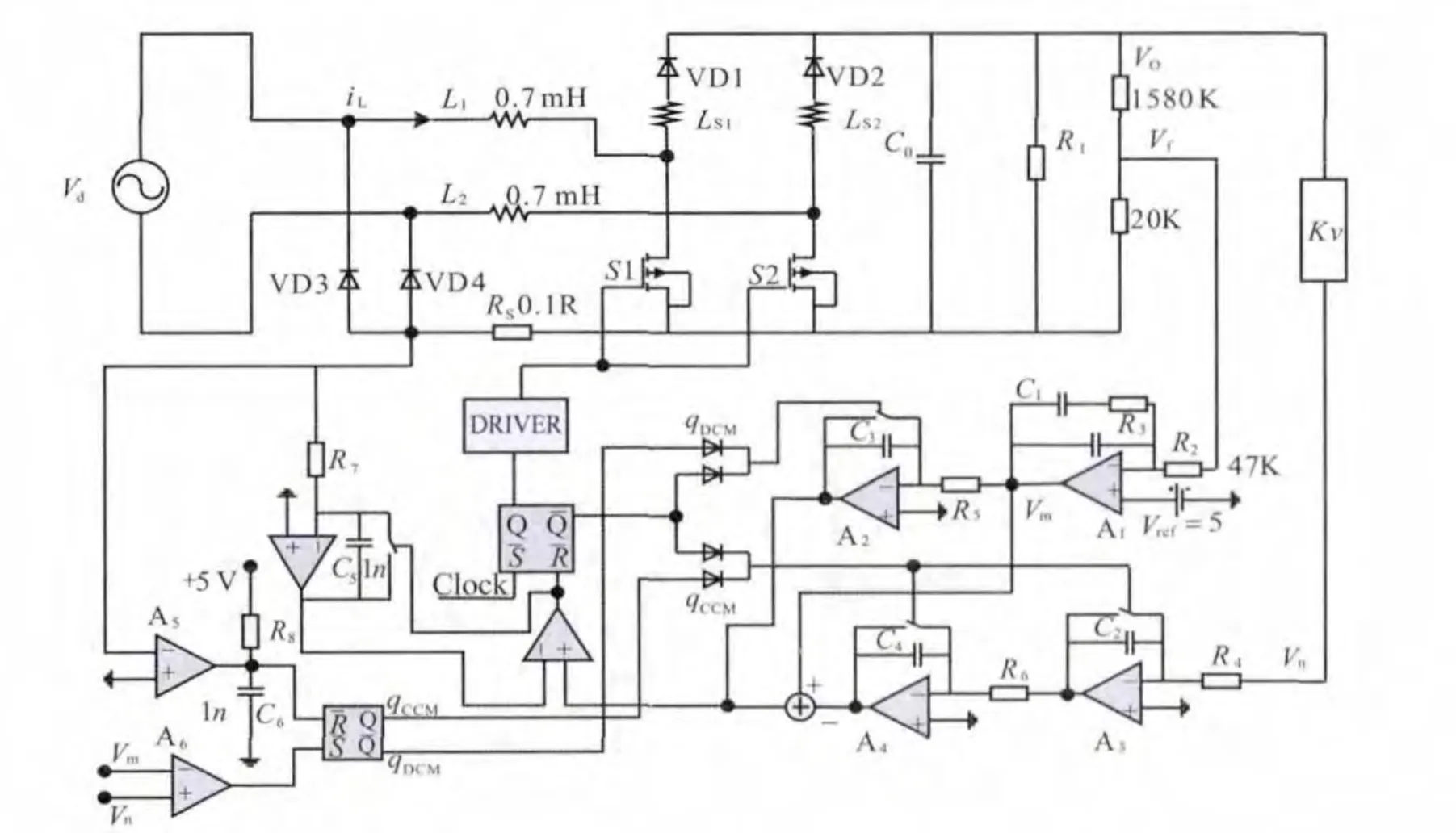
图1 HCM模式下的单周控制原理图

（2）工作原理

在时钟信号的作用下，一开始开关管导通，在此期间，载波输出大于电流传感器的检测值，在TON的末端，电流检测值等于载波输出，A7输出为‘0’，触发器复位，开关管关断。若在TON期间，检测到输入电流为零或负值，A5输出为‘0’qDCM=1，进入DCM模式，若无，则维持CCM模式；若检测到Vm大于Vn时，A6输出为‘0’，qDCM=1,进入 CCM模式。 工作模式的切换仅发生在开关管导通期间，其工作模式的切换是通过检测二极管的反向恢复电流实现的。

1.4 二极管反向恢复问题的抑制

高频功率二极管在电力电子装置中的应用极其广泛，但二极管在由导通变为截止状态过程中，存在反向恢复现象，这会引起二极管损耗增大，电路效率降低以及EMI增加等问题，这一问题在大功率电源中更加突出。若将电路工作在DCM模式下，当开关管S开通时，二极管的电流已经下降到零，这时不存在反向恢复电流流入开关管，但是DCM模式下PFC电感上电流脉动很大，其峰值电流为平均电流的两倍，增加了开关管和输出二极管的电压应力。本文采用HCM单周控制和串联饱和电抗器相结合的方法来解决这一问题，工作过程如图2所示。第Ⅰ阶段，通过D的电流很大，电抗器LS饱和，电感值很小；第Ⅱ阶段，当二极管电流开始下降时，LS仍很小；第Ⅲ阶段，二极管电流反向，此时变换器被切换至DCM模式，反向恢复过程开始，LS值很快增大，抑制了反向恢复电流的增大，这样就使电流变成di/dt较小的软恢复，使二极管的损耗减小，同时抑制了一个重要的噪声源；第Ⅳ阶段二极管反向恢复结束；第Ⅴ阶段二极管再次导通，由于电流增大，LS很快饱和。从图3所示可以看到在开关开通前二极管上的电流已基本恢复到零，二极管的方向恢复电流得到抑制，与前面理论分析相符。

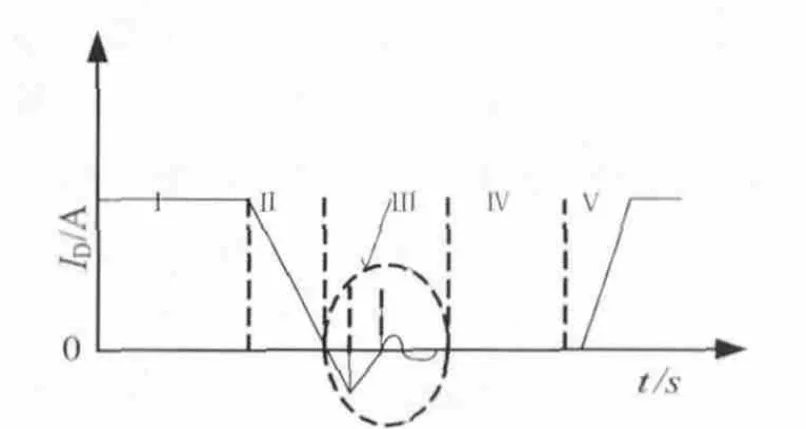
图2 反向恢复电流

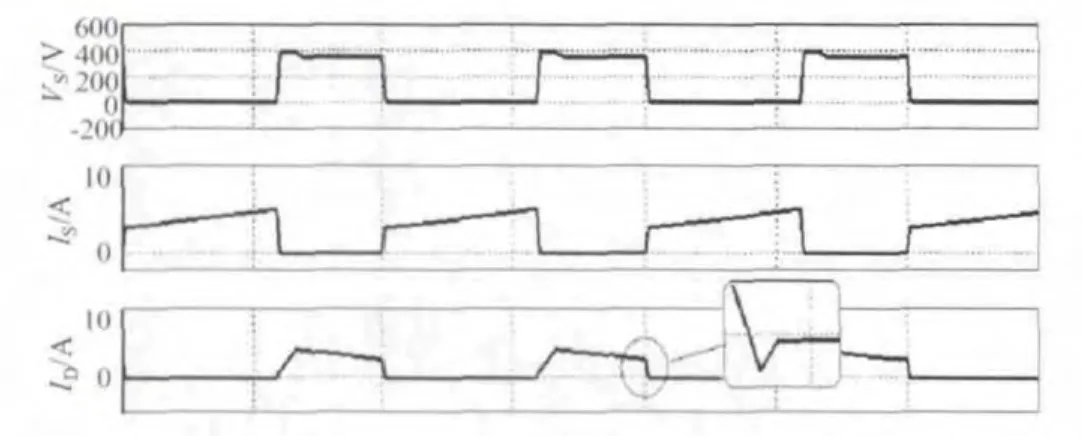
图3 反向恢复过程波形图

2 稳定性分析

提高系统稳定性的关键在于电压反馈环节的设计。电压反馈环原理框图如图4所示。

（1）开环增益

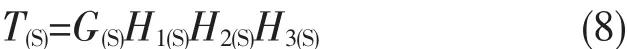
（2）输出分压传递函数

对于恒定功率负载时，传递函数G(S)H3(S)为：

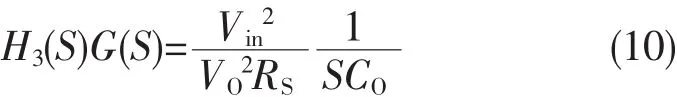
（3）误差传递函数

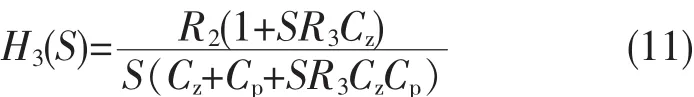
H2(S)是为了提供足够的相位裕度和带宽限制，一般把H2(S)的零点频率设置为小于10 Hz以便得到足够的相位裕度极点设置为1 kHz（远低于开关频率）以避免开关噪声的影响[5]。

系统的开环传递函数为：

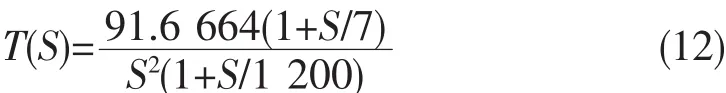
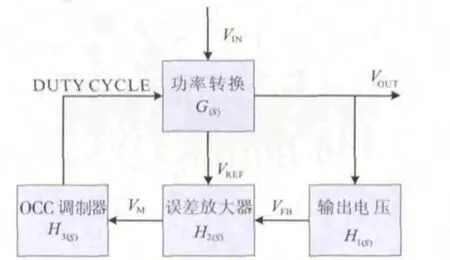
图4 电压反馈环原理图

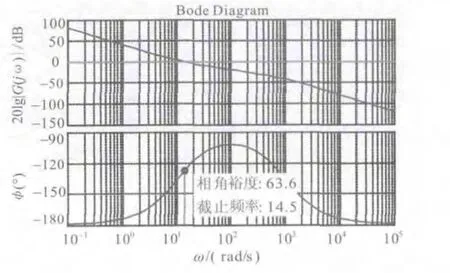
图5 系统开环Bode图

系统的开环Bode图如图5所示。由于此系统开环传递函数的特征根全部位于S平的左半部分，所以开环稳定。根据Bode图和奈氏判据可知在开环对数幅频特性大于0 dB所有频段里，对数相频特性曲线φ(ω)与-180°线的正负穿越次数相等，都为零，所以该系统闭环仍是稳定的[6-7]。

3 仿真结果

采用Matlab/SIMULINK对HCM单周控制的无桥PFC电路进行了建模仿真。输入电压Vin为85～264 V，升压电感 L=750 μH，输出电压 VO=385 V，输出电容CO=1 000 μF/450 V，工作频率为100 kHz,输出功率300 W。

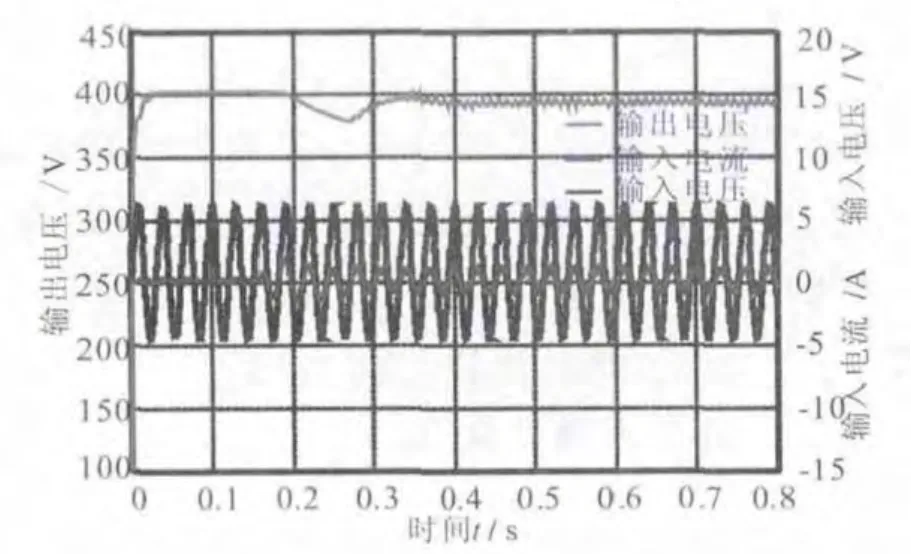
图6 空载到满载跳变波形

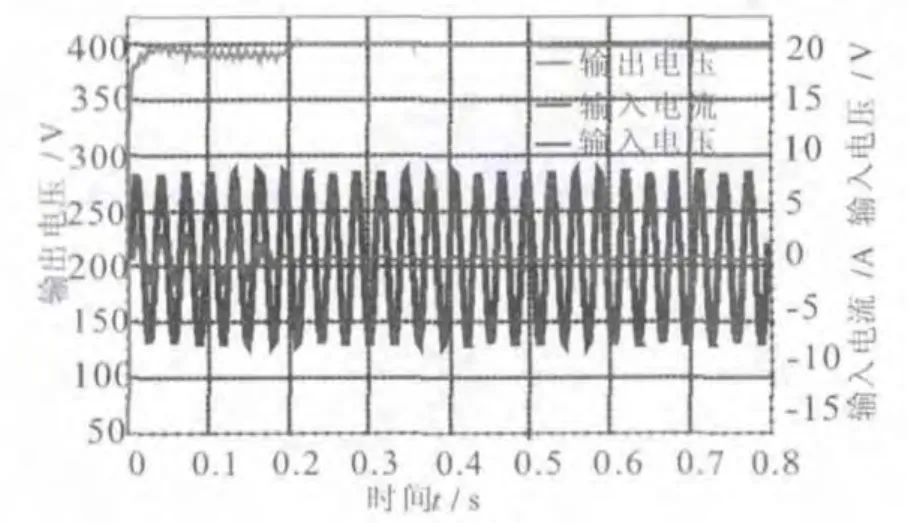
图7 满载到空载跳变波形

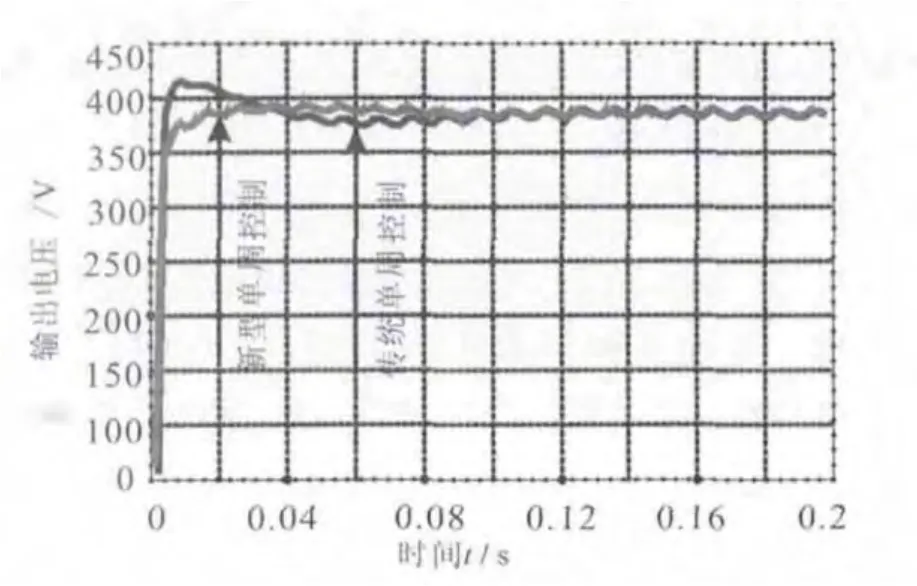
图8 控制算法输出响应对比波形

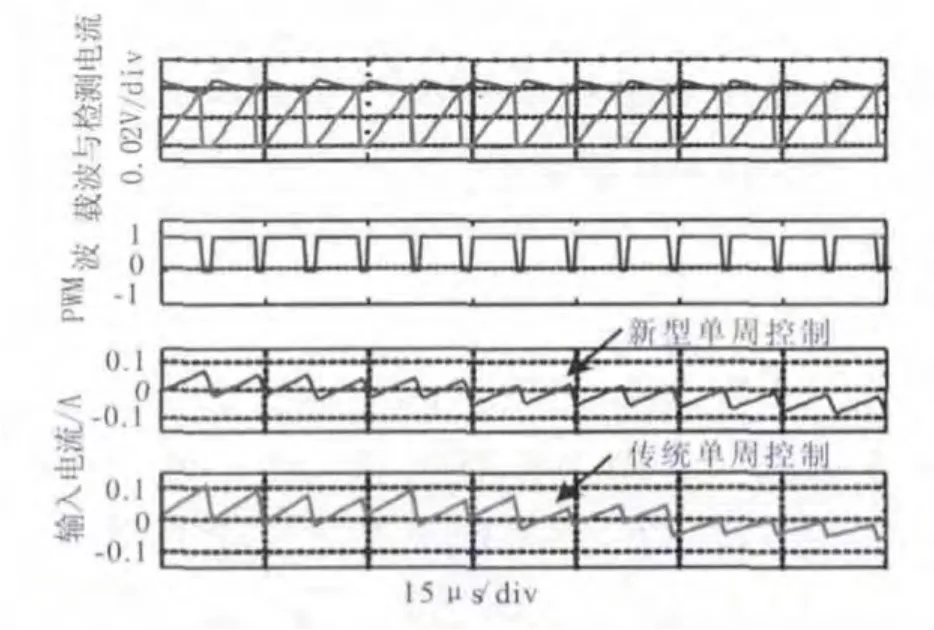
图9 控制算法输入电流过零对比波形

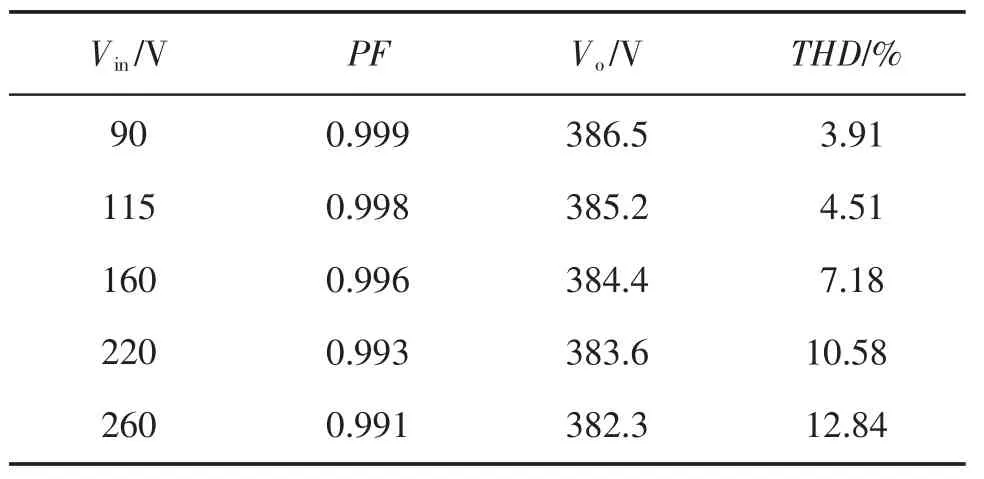
表1 目标参数与网压关系

主要对系统满载时的电压、电流，及满载到空载、空载到满载的跳变进行仿真。从图6、图7可以看出：在负载变化比较大时，回路调整到稳定的时间较短，且电路最终都能把输出电压调整到额定值附近，说明整个电路收敛，最终都能稳定工作；从图8可以看出改进型单周控制比传统控制算法具备更快的输出响应，从图9可以看出传统控制算法存在输入电流过零畸变问题，新型单周控制下输入电流波形平滑过渡，削弱了二极管反向恢复问题。

当负载为满载300 W、开关频为100 kHz时，输入电压和总谐波畸变率(THD)的测试结果见表1，可以看出在输入电压为AC 115 V、满载输出时，THD＜5%，且此时的功率达到0.998，表明系统的EMI问题得到了很好的抑制，抗干扰能力强。

4 结论

分析了新型单周期控制的无桥Boost APFC电路的基本工作原理，在此原理基础上搭建模型，并对设计电路进行了仿真。仿真结果表明：基于新型单周期控制的APFC电路与传统单周控制电路相比，动态响应更快，无二极管反向恢复问题，且抗干扰能力强。

[1]Smedley K M,Cuk S.One-Cycle Control of Switching Converters[J].IEEE Transactions on Power Electronics,1995,10(6)：625-633.

[2]Lai Zheren,Smedley K M.Time Qantityone-Cycle Control for Power Factor Correctors[J].IEEE Transactions on Power Electronics,1997,12(2)：369-375.

[3]Edison Roberto,Melo Bento.Hybrid One Cycle Controller for Boost PFC Rectifier[J].IEEE Transactions on industry application.2009,45(1)：268-277.

[4]Bing Lu,Ron Brown.Bridgeless PFC Implementation Using One Cycle Control Technique[J].IEEE Transactions on Power Electronics,2005,5(3)：812-817.

[5]刘桂花,刘永光,王卫.无桥Boost PFC技术的研究[J].电子器件,2007,10(5)：1918-1921.

[6]皇金锋.全桥式DC/AC/DC变换器的建模与仿真[J].计算机仿真,2013,30(4)：336-338.

[7]罗海波.PID控制器设计与仿真研究[J].计算机仿真,2012,29(2)：345-348.