小波分析在低压负荷预测数据处理中的应用

冷建伟，傅祥廉

(天津理工大学自动化学院，天津 300384)

引言

随着智能电网的提出及实施，低压用户对于电能可靠性和经济性的关注日益增长。由此，对低压电力负荷短期预测的研究应运而生，通过负荷预测可帮助用户对电能有效利用制定规划。

小波变换作为近10多年来迅速发展的一种信号处理方法在各工程领域中受到了广泛的重视[1]。小波变换在时间、频率两域都具有表征信号局部特征的能力，适合探测正常信号中夹带的瞬间反常现象并展示其成分，而且在对含有白噪声的波形进行阈值滤波，能有效处理历史数据，为负荷预测模型提供可靠的数据。

1 小波变换原理

小波变换是一种积分变换，它实质是加窗的Fourier变换(WFT)的发展与演变，它比加窗的Fourier变换更优越[2]。加窗Fourier变换的思想是：选择一个时频局部化的窗函数，假定分析窗函数g(t)在一个短时间间隔内是平稳的，移动窗函数，使f(t)g(t)在不同的有限时间宽度内是平稳信号，从而计算出各个不同时刻的功率谱。由此可知，一旦窗函数其分辨率也就确定了，若需改变分辨率则需要重新选择窗函数。小波变换使用一个窗函数，即小波函数，时频窗面积不变，但形状可改变，小波函数根据需要调整时间与频率分辨率，具有多分辨率分析的特点。同时小波变换由于能够任意选取变换的窗口函数，变换、重构后的数据点和原信号点为一一对应，其中可通过合适的阈值选取进行有效去噪。

1.1 离散小波变换

在小波分析中，如果ψ(t)∈L2(R)，其中Fourier变换为(ω)满足容许性条件

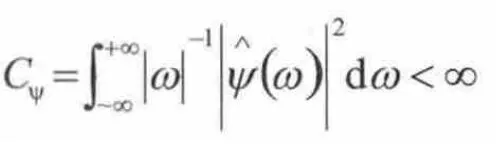
即 Cψ有界，则称ψ为一个基小波，将基小波经过伸缩和平移后，就可以得到一个小波序列

其中，a，b∈R 且 a≠0。

在实际应用中，通常采集数据为离散形式，所以采用离散小波变换（DWT）。此时，通常取a=a0m，b=nb0a0m，m,n∈Z，则

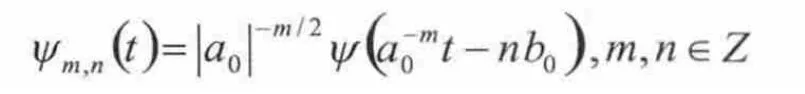
相应离散小波变换为：

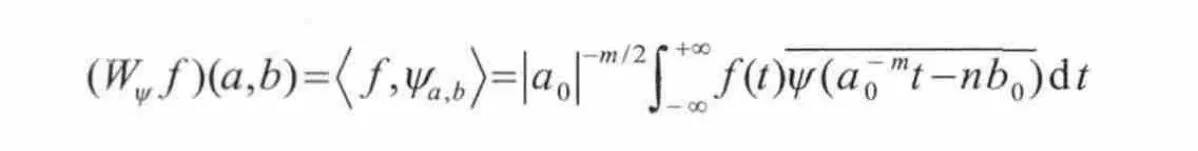
1.2 小波变换阀值消噪

在小波变换中，对信号去噪实质上是抑制信号中无用的部分，即小波分解高频系数的阈值量化。阈值去噪是对各个分解尺度下的高频系数选择一个阈值进行量化处理。在文献[3]中详细介绍了阈值消噪的原理及实现方法。其中，以硬阈值方法及软阈值方法为主要去噪方法。对于一个带白噪声的一维离散信号模型：

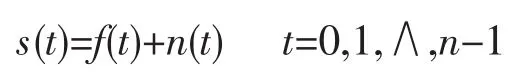
式中：s(t)为原始含噪声信号；f(t)为有用信号，n(t)为噪声信号。

在对含噪信号s(t)进行离散小波变换后，得到各尺度小波系数后，对各尺度小波系数wj,k进行阈值处理，得出估计小波系数尽量小。 其中硬阈值方法中使用的估计小波系数的方法为：

软阈值方法中使用的估计小波系数的方法为：

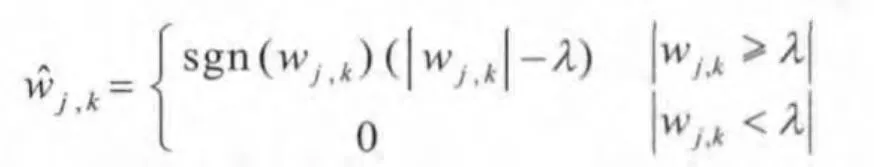
2 实例分析

在天津一大型企业中建立能源检测系统，因电表计量采用RS485串口采集用电量数据，所以采用串口服务器准确采集电量数据。实现以分钟为单位计量用电量数据。

使用该系统进行电量数据采集后，对该厂某车间用电量进行负荷预测前期数据处理。该车间用电负荷除照明外亦有大功率电磁设备工作，采用该车间2013年3月用电量数据，以1 h为单位共720 h，即720个数据点如图1所示：

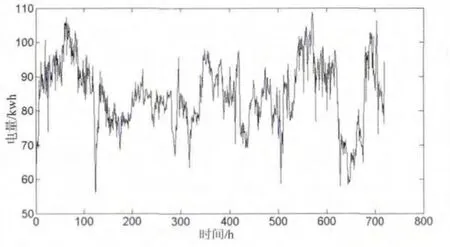
图1 原始信号波形

由图1可知，该原始信号中含有大量白噪声，且为非平稳信号波形。通过分析图中波形，该波形具有以下特征：

（1）波形呈一定的规律性，结合该企业试验记录，在三月有三次大型设备检测用电负荷明显上升，周末因休息用电负荷明显减少。符合本用电负荷原始信号曲线基本走势。

（2）针对电量负荷分配有60%的用电量为大型试验设备消耗，其他负荷为照明负荷。大型试验设备消耗显示于低频分量的改变，照明导致有高频分量。

（3）每日损耗形成的曲线根据不同时间而变化，通过局部放大波形可看出，在试验设备停止工作的夜间，用电负荷相对白天负荷下降不少。

针对该波形，为避免普通离散小波不具有时移不变性而具有平移敏感性，选用平稳离散小波变换。对于平稳离散小波变换，原始信号需要能够平分为2^K份，所以必须对信号长度进行延拓以适应平稳离散小波变换需要。其延拓后波形如图2所示：

图2 拓展后波形

利用db3小波奇函数对信号执行三层小波分解，如图3所示，

为使阈值除噪效果更好且不失真，分别尝试软阈值与硬阈值去噪对比。

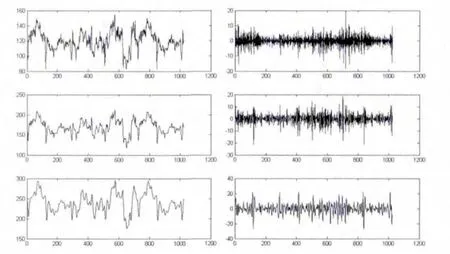
图3 三层小波分解及杂波信号

对于非平稳波形，使用硬阈值去噪情况下滤去各小波分解频段中的低频噪声后无法有效解决高频噪声造成的影响，如图3所示：

而使用软阈值处理能对非平稳波形具有良好的消除噪声作用，且保留了能反映原始波形特征的峰值点。如图4所示：

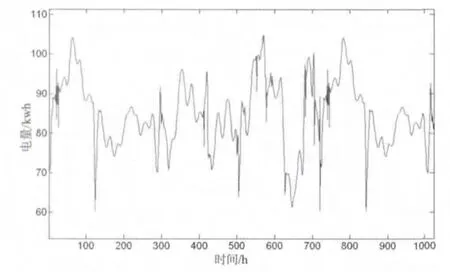
图3 硬阈值去噪后波形

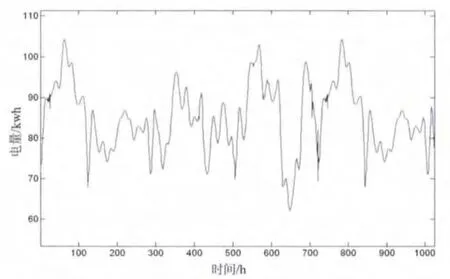
图4 软阈值去噪后波形

3 结论

通过以上分析，小波变换能有效分解出原始信号中有用的信号部分以及含噪声的突变部分。通过对硬软阈值处理对比，发现软阈值能够使估计信号实现最大均方误差最小化，降低了少数噪声的干扰，对于非平稳波形具有良好的消除噪声效果，且能保留原波形中有效的峰值点不失真。经过小波分析后得出的曲线为负荷预测模型选取提供良好的依据。

本文仅根据历史负荷数据通过小波变换进行数据处理，但完善的负荷预测数据处理还需要结合实际气象、季节等对负荷使用影响较大的条件。在数据处理中可将这些条件进行模糊化处理为负荷预测提供更可靠的数据支持。

[1]宋超，黄民翔，叶建斌.小波分析方法在电力系统短期负荷预测中的应用[J].电力系统及其自动化学报，2002（6）：8-12.

[2]张熙.小波变换在电力系统负荷状态监视和故障诊断中的应用[J].电工电气，2010（10）：47-49.

[3]向晓燕,谭子尤,张书真.基于小波的阈值消噪方法讨论及实现[J].电子技术，2007（17）：172-173.

[4]陈志业，牛东晓，张英怀.电网短期电力负荷预测系统的研究[J].中国电机工程学报，1995,15(1)：30-35.

[5]Donoho D L,John stonel.Wavelet Shrinkage Asymptopia[J].Journal of Royal St-Atistical,Society,1995,57(2)：30-36.