模态试验过程控制研究

姜 睿 王 婧 赵凤飞

（沈阳发动机设计研究所，辽宁 沈阳 110015）

0 前言

燃气涡轮发动机作为当今社会重要的动力提供者之一，在航空、船舶以及电力等领域都有着广泛的应用。燃气涡轮发动机通过转子的高速旋转，吸入并压缩空气，然后通过燃烧驱动涡轮以达到提供动力的目的[1]。高速旋转必然带来振动问题。气流在经过高速旋转的转子之后会形成一种周期性激振力作用于发动机构件上（如转、静子叶片、机匣等），当激振力频率与构件的某阶固有频率接近或吻合时，就可能导致该构件发生共振，从而导致该构件出现高循环疲劳失效。据统计，疲劳是燃气涡轮发动机最主要的失效模式，基本占据发动机失效模式的一半，而其中又有一半左右的失效模式为高循环疲劳失效模式（见图1）。

图1 燃气涡轮发动机失效模式及其比例[2]

随着燃气涡轮发动机技术的发展，其推重比越来越高，随之而来的则是越来越高的压气机增压比、涡轮前温度以及越来越轻的结构重量。这些改进往往恶化了发动机的工作条件，提高了发动机构件的应力水平。这就要求在新一代发动机结构设计中更加重视关键部位的设计细节，以确保发动机的可靠性和耐久性[3]。

综上所述，研究发动机某些关键构件的固有振动特性，分析其在发动机工作时所可能出现的高循环疲劳失效对于提高发动机的可靠性和耐久性是十分必要的。

模态是构件的的固有振动特性，一般包括固有频率以及相对应的固有振型与阻尼系数。所谓模态分析就是将线性定常系统振动微分方程中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，以便求出系统的固有频率、固有振型、阻尼系数等模态参数[4-5]。

目前，国内外针对发动机结构件的固有振动特性分析主要有理论模态分析与试验模态分析。这两种分析应用于发动机研制的不同阶段。理论模态分析主要应用于发动机初始设计阶段，可在前期设计阶段规避所可能出现的结构件高循环疲劳失效风险；试验模态分析应用于发动机研制试验验证阶段，在理论模态分析基础上，对发动机真实结构件进行动特性分析，进一步规避其高循环失效风险并可有效应用于有限元模型修正，提高理论模态分析的准确性。

二十几年来，随着计算机技术，FFT分析仪，高速数据采集系统以及振动传感器激振器等技术的发展，模态试验及分析技术得到了很快的发展，受到了机械、电力、建筑、水利、航空、航天等许多领域的高度重视。进行一个模态试验，要想取得最佳的试验结果，仅仅懂得试验过程和试验分析的步骤是远远不够的，在试验中很多对细节的控制都会对试验的结果好坏有很大影响。研究模态试验中如何通过一些细节的控制对优化试验结果有着重要的实际意义[6]。

1 试验对象、试验方法及试验系统简介

本文模态试验对象为某型燃气涡轮发动机风扇机匣组件。

机匣是航空发动机及地面燃机的主要承力件[7]，与发动机转子以及承力轴承等共同组成了转子－支承－机匣系统[8]，是支承整个发动机传力的重要组成部分；同时，机匣也是形成发动机流道的主要构件。受流道内气体激励、转子不平衡等作用，机匣都可能产生振动。因此对机匣进行模态试验分析，得到其固有振动特性是必要的。

常用的模态试验方法主要有三种，分别为单输入多输出（SIMO）、多输入多输出（MIMO）以及多输入单输出（MISO）[9]。由于风扇机匣为金属构件，刚性尚可，考虑试验复杂程度及周期，选择单输入多输出方法进行试验。试验过程中采用2302-10型力锤进行激励，信号拾取采用B&K 4508B智能型ICP传感器，后端数据采集和处理采用B&K公司PLUSE数据管理系统和ME’scope模态参数分析系统。模态试验系统简图见2。

图2 模态试验系统简图

2 不同锤头对试验结果的影响

力锤作为激励系统，其锤头的选择对于试验结果存在重大影响。不同类型的锤头激振频率范围是不同的。通常来说，硬度越高的锤头所能激励的频率范围就越大。由于在采用锤击法进行模态试验时，需要进行数百次甚至数千次的敲击，锤头过硬就可能存在破坏试验件的风险，因此锤头的选择在确保所激励的频率范围足够的基础上应越软越好。

以风扇一级机匣为例，采用钢锤头与铝锤头分别进行模态试验，试验分析带宽为6.4kHz，试验频响函数见图3。

图3 钢（上）铝（下）锤头激励频响函数

从试验结果可以看出，在6.4kHz频率范围内，采用钢锤头和铝锤头得到的试验结果是一致的，因此对于该试验，采用铝制锤头即可，既不影响频率分析范围，还可降低敲击导致破坏机匣的风险。

3 模型网格点数对试验结果的影响

机匣作为薄壁圆筒件，其标准固有振型为沿周向出现的梅花瓣形，且瓣数（m）通常随着频率的升高而增加。为了得到机匣的高阶振型（瓣数较多），用于模态试验的模型所需的网格点数应非常多。但网格点数不是越多越好，因为网格点数越多，试验周期就会越长，且当网格点数达到一定程度，两个网格点之间的距离就会很小，这就导致在传感器附近的网格点，其激励信号难以控制（激励太大将超过传感器量程，激励太小则无法有效激励试验件）。因此，网格点数的选择对于模态试验结果也很关键。

同样以风扇一级机匣为例，分别建立周向网格点数为23和92的线模型进行模态试验，分析带宽为1.6kHz，表1列出了部分频率结果，图4为采用这两种模型得到的3阶典型振型图。

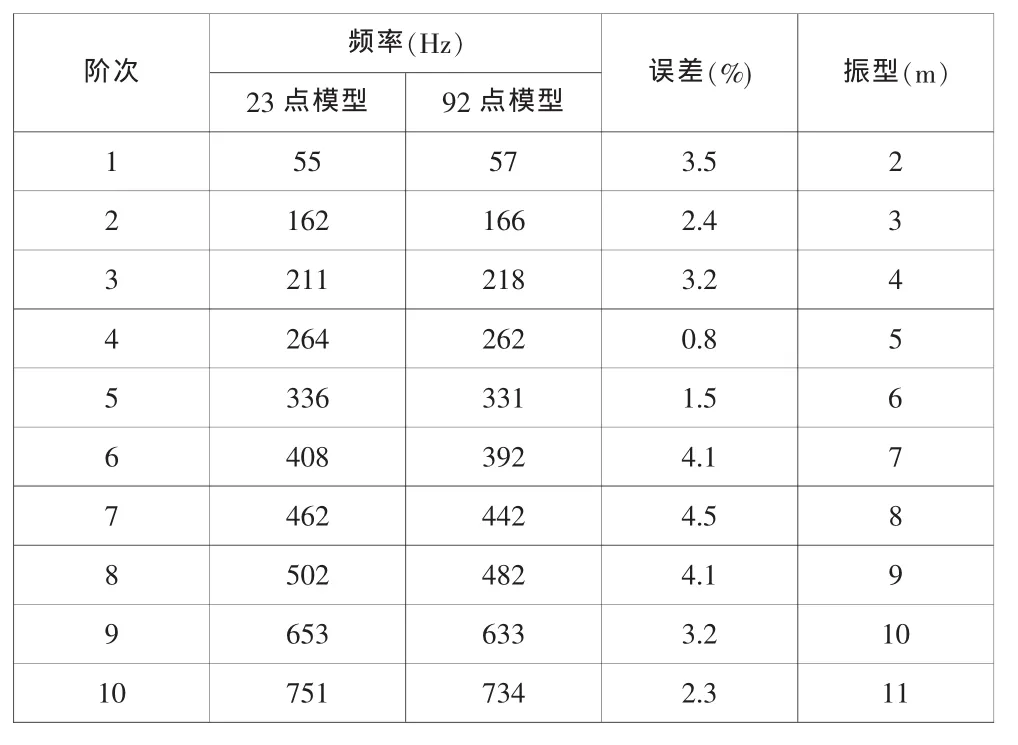
表1 前10阶模态试验结果

从该试验结果可以看出，网格点数的不同对机匣的固有频率结果并无太大影响（误差在5%以内），但对振型结果影响较大。从图4来看，瓣数少于11的振型（图4左、中），通过两种不同模型所得到的结果是一致的；对于瓣数为12的振型（图4右），通过23个网格点的模型无法有效得到。

根据该试验结果可以得到如下试验结论：对于机匣类的薄壁圆筒形试验件，用于模态试验模型的周向网格点数最少必须大于瓣数的2倍。换而言之，若所需得到的试件振型具有N个梅花瓣，那么在建模时，模型周向网格点数必须大于2N。

图4 23点（上）与92点（下）模型同阶振型图

4 模型简化对试验结果的影响

整体机匣试验件不仅直径较大而且轴向长度也较长。针对这类试验件，如果采用整体建模进行模态试验，不仅试验周期长，而且对于高阶振型，往往识别效果很差。

以风扇整体机匣为例，以圆柱面为基础建立其整体模型，周向网格点92个，轴向网格点10个，共计920个网格点，模型图见图5。

图5 风扇机匣整体模型图

采用锤击法进行模态试验，部分试验结果见表2。

表2 整体模型部分典型模态试验结果

从试验结果来看，由于试验件尺寸较大，因此利用力锤无法充分激励该试验件，导致高阶振型无法分辨。

面对这种情况，可以考虑采用简化模型、多次试验，最终综合试验结果的方法来解决。

仍以风扇整体机匣为例，它由风扇1、2、3级机匣通过安装边连接而成。对于每一段机匣而言，由于其轴向长度与直径的比值较小，可以假设其在轴向各截面不会出现不同梅花瓣数的振型。基于上述假设，对风扇整体机匣进行3次周向模态试验，分别对应风扇1～3级机匣，最后进行整体轴向模态试验。最终对这4个模态试验的结果进行综合分析。

对于风扇1～3级机匣周向模态试验，选取机匣中部一圈建立网格点数为92的线模型，对于整体机匣轴向模态试验，沿机匣轴向建立一条网格点数为20的线模型。所有模型网格点数相加仅为296点。采用锤击法分别进行模态试验，部分典型试验结果见表3。

以固有频率为331Hz左右的振型为例，根据整体模型所得到的振型见图6（其中3级机匣在上，1级机匣在下），根据简化模型得到的振型见图7（从左到右分别为1、2、3级机匣周向和整体机匣轴向振型）。

表3 简化模型部分典型模态试验结果

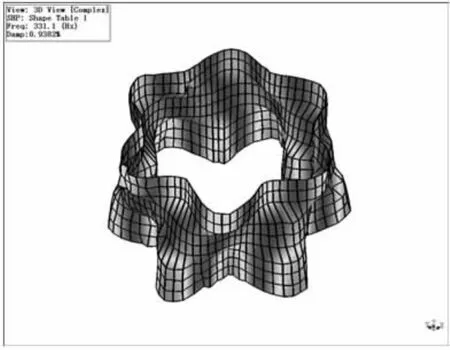
图6 风扇机匣振型图（整体模型）

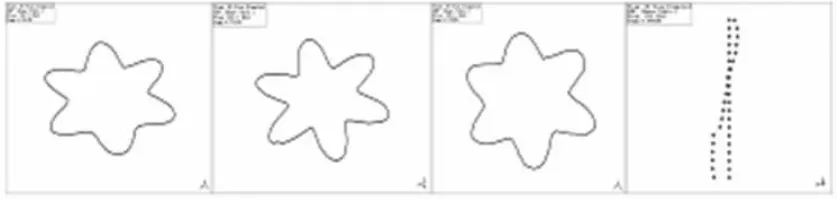
图7 风扇机匣振型图（简化模型）

从图6可以看出，该阶振型为复合振型，其中轴向节线应在2级机匣上，1、2、3级机匣的波瓣数为6。而综合图7中的四个模态试验结果也可以得到相同的结论。

据此可以推断，表3中频率为730Hz左右所对应的振型应为1级机匣周向11个瓣，2级机匣周向10个瓣，3级机匣周向12个瓣，且沿轴向有2个节点。而该频率所对应的振型通过整体模型无法有效获得（见表 2）。

5 结论

（1）对于风扇一级机匣，在6.4kHz频率范围内，采用钢制锤头与铝制锤头所得到的模态试验结果一致，因此可以采用铝制锤头进行试验。

（2）对于薄壁圆筒形构件，试验模型的周向网格点数至少应超过所关心振型瓣数的2倍以上，否则无法有效得到高阶振型；但点数多少并不影响频率结果。

（3）对于尺寸较大且直径与轴向长度比值较小的薄壁圆筒形构件，可以考虑采用简化模型后多次试验并最终综合所有试验结果的方法来获得较为精确的高阶振型并缩短试验周期。从本文试验结果来看，对频率范围在1.6kHz以内的振型还是适用的。如果所关心振型的频率超过1.6kHz，由于薄壁圆筒形构件的固有频率非常密集，想在分别进行的模态试验结果中找到代表相同振型的频率就会变得非常困难。这种情况下，采用激振器代替力锤进行激励可能会得到更好的结果。

［1］Pericles Pilidis,J.R.Palmer(2012).Gas Turbine Theory and Performance[D].Cranfield University.

［2］ S.Suresh.Fatigue of Materials[M].2nd ed.Cambridge University Press,1998.

［3］高德平,等.航空涡喷、涡扇发动机结构设计准则（研究报告）:第四册[Z].北京:中国航空工业总公司发动机系统工程局，1997.

［4］沃德·海伦,斯蒂芬·拉门兹,波尔·萨斯.模态分析理论与实验[M].北京:北京理工大学出版社,2001.

［5］傅志方,华宏星.模态分析理论与应用[M].上海:上海交通大学出版社,2000.

［6］王婧.某燃机涡轮后机匣试验模态分析研究[C]//中国航空学会第八届轻型燃气轮机学术交流会.2013.

［7］航空发动机结构设计手册:第17册 载荷及机匣承力件强度分析[M].北京：航空工业出版社，2001.

［8］郑旭东，张连祥，刘廷毅.航空发动机整机振动特性及应变能计算与分析[J].航空发动机，2000(2)：42-46.

［9］张新玉，张文平，李全,等.圆柱形薄壳结构的试验模态分析方法研究[J].哈尔滨工程大学学报，2006，27(1):20-25.