基于载波平滑的电离层误差技术研究

吕超李斌

(中国电子科技集团公司 第二十研究所，陕西 西安710068)

0 介绍

GPS系统作为高精度的全球导航定位系统，已经成为军用、民用导航、测量定位的主要技术手段，但是在应用GPS技术进行高精度导航定位测量中，地球电离层对GPS导航电文造成的时间延迟在最恶劣的条件下可达到300ns左右。为了消除电离层的影响，通常采用的方法有：数学模型估计电离层延迟、载波平滑码伪距结合差分技术等等，数学模型消除电离层影响通常用于单点绝对定位，可粗略的消除电离层延迟误差，而载波平滑伪距差分技术可大大降低电离层延迟误差的影响，但是在平滑过程中将会引入额外的算法误差，此误差量级在1～2米。本文首先简单介绍数学模型经验公式和差分法消除电离层延迟，然后通过数学推演计算出额外的算法误差的数学表达式，并在传统的差分技术中予以消除，以提高定位精度。

本文由五部分组成，第一节给出应用背景和现有研究的介绍，第二节给出非差电离层修正模型，第三节给出单频差分电离层修正算法，包括静态差分电离层修正和动态差分电离层修正，并分析分析载波平滑和运动速度对电离层修正值的影响，本文结论将在第四节予以总结。

1 非差电离层修正

对于单点绝对定位，当使用单频接收机时，由于单频接收机无法利用观测量的值解算出两个频点上的电离层延迟，因此只能借助一些数学模型来估算、校正电离层延迟。单频接收机垂直方向电离层延迟模型的数学表达式为：

倾斜方向的电离层延迟为：

2 单频差分电离层修正

2.1 静态差分电离层修正

其中：Δx表示基准站A与用户站B对应的刺穿点之间的距离。当用户站从自己的伪距中消除掉基准站播发的修正值后，在将上述残余电离层延迟消除掉。

图1 差分系统原理

2.2 动态载波平滑电离层修正

2.2.1 载波平滑算法

载波相位平滑码伪距的主要目的是利用低噪声的载波相位观测量来降低码伪距的多路径和热噪声。

对每个接收机通道（接收机u和卫星i），在历元k，使用具有时间常数τ的滤波器，采样间隔T：

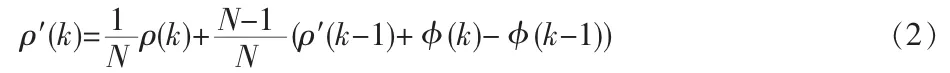
其中：

N=τ/T，ρ′表示平滑伪距。

将（2）载波平滑公式改写为下式：

2.2.2 载波平滑后电离层延迟

由于基准站在发送修正值前以及用户站在使用伪距定位前都需对伪距进行上述载波相位平滑，而上述载波相位平滑后的电离层延迟与未平滑的原始伪距不同，深层次的原因是载波相位和码伪距的电离层延迟符号相反，因此在差分单点定位中，需进行考虑。

设载波平滑伪距方程式为：

原始伪距观测方程式为：

其中，R(k)表示真实几何距离，接收机钟差，卫星钟差，对流层延迟，星历误差之和，θ(k)表示由于载波相位平滑所引起的电离层延迟改变量，ε^(k)表示载波平滑伪距的多路径，热噪声误差，ε(k)表示原始伪距的多路径热噪声误差。

由于载波相位的多路径及热噪声误差相对于伪距很小，可以忽略。故（6）中没写出。

为了分析 θ(k)的大小及影响方式，将式（4）、（5）、（6）代入式（3），可得：

整理可得：

令：

设移动用户在k时刻处于a点对应的电离层为Ia(k)，k+Δt时刻处于b点，对应的电离层为Ib(k+Δt)，这样式（9）可变换为：

（10）式两边令Δt→0取极限，可得载波平滑后电离层变化量的微分方程式：

这是一个非齐次一阶为非方程，采用待定系数法求解，得到平滑误差：

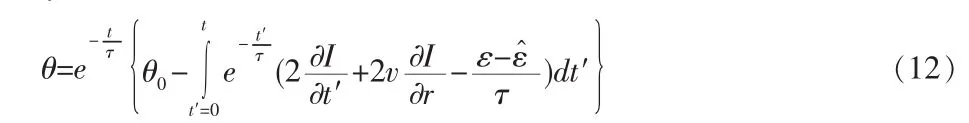
设电离层时间梯度为k1，即：

我们忽略其他因素的的影响包括多路径热噪声、空间梯度和解的初始值。依据公式（10）得到时间梯度在载波平滑过程中引起的电离层额外误差，该误差可表示为：

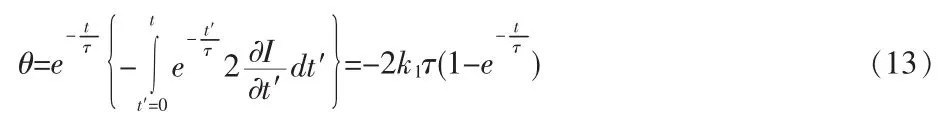
随着时间的推移，该公式表示此额外误差会趋近于一个常数，该常数为负的两倍电离层时间梯度和时间常数的乘积，到达稳态时，该误差为：

平滑后的电离层误差残差随时间的变化如图 2，其中电离层时间梯度为5mm/s.，其中空间梯度为0.

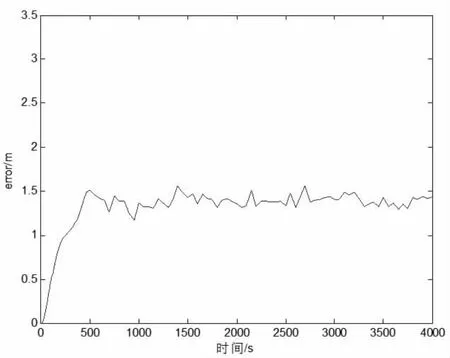
图2 τ=200s平滑后电离层误差残差随时间的变化,其中空间梯度为0

下面我们分析电离层空间梯度的影响。设电离层空间梯度为：

同样的，我们忽略其他因素包括多路径热噪声、时间梯度和解的初始值。根据公式（12）得到空间在载波平滑过程中引起的电离层额外误差，该误差可表示为：

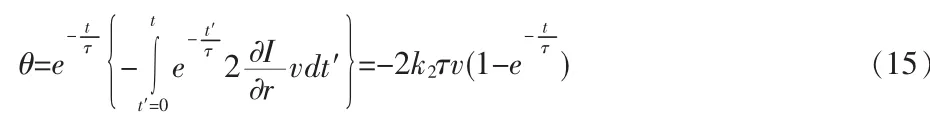
到达稳定状态时此额外误差可表示为：

平滑后的电离层误差残差随时间的变化如图 3，其中电离层空间梯度为1.25cmm/km，用户速度为300m/s，时间梯度为0。

图3 平滑后电离层误差残差随时间的变化,其中时间梯度为0

从该公式中可以看出，电离层空间梯度对高速用户的影响更大，而对于静止用户没有影响。

综合以上分析我们可得运动用户采用载波相位平滑伪距修正时，由于载波相位所引起的残余电离层误差总的表达式为

其中，Fpp表示倾斜因子，将垂直电离层延迟转化为倾斜电离层延迟，具体表达式为：

R为地球椭球体半径取6378.1363km，h为电离层平均高度取350km，见图 4。

图4 区域电离层关系示意图

3 结论

通过本文算法研究可见，非差分的电离层延迟一般通过经验公式估计得出，而静态差分后电离层延迟误差将大大减小，其值与电离层空间梯度和基准站和移动站的相对距离有关。对于动态载波相位平滑伪距后，其电离层修正量的值与载波平滑的滤波时间和用户运动速度有关。

［1］薛瑞.GBAS算法研究报告[M].北京：北京航空航天大学.

［2］谢刚.GPS原理与接收机设计[M].北京：电子工业出版社，2011，07.

［3］王刚，姬剑锋，冯来平，等.EGNOS电离层延迟改正数分析[J].西安：西安测绘研究所卫星导航定位实验室，2004，06.

［4］Jock R.I.Christie,Ping-Ya Ko,Andrew Hansen etc.The Effects of Local Ionospheric Decorrelation on LAAS:Theory and Experimental Results[C]//ION NTM-99.California January 1999.

［5］余明，郭标明，过静珺.GPS电离层延迟Klobuchar模型与双频数据的解算值的比较与分析[J].测绘通报，2004(06).