基于数据融和的差分技术研究

路阳李斌

（中国电子科技集团公司 第二十研究所，陕西 西安710068）

0 介绍

在全球卫星导航定位系统中，为了提高定位精度，设计了LAAS局域增强算法，其核心是差分处理技术，差分算法的大概处理过程是通过地面将差分处理结果通过广播链路（VDB）发送到机载接收机中，机载接收机利用该修正信息完成本机位置、时间和速度参数的解算，达到改善定位精度和完好性指标等目的。它通过地面部分的增强处理实现对卫星导航信号的增强，主要的作用方式是地面接收卫星导航信号，依据地面站的准确位置形成各导航卫星伪距和载波相位的精确修正，连同卫星完好性和进近参数的处理共同形成差分修正信息。

1 差分系统原理

在平滑后，地面站将生成的针对每颗可见卫星的差分信息。首先，地面站计算参考接收机g到卫星i的几何距离。

其中，xi是从导航电文获得的卫星位置，xg是接收机的精确三维位置坐标。差分改正值可以计算为：

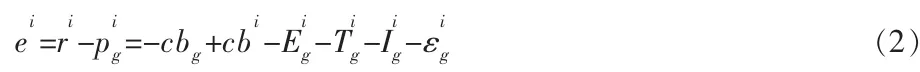
然后用户将使用该改正值修正自己的平滑伪距，修正后的用户平滑伪距可以表示为：

在该式中，由于用户与地面站相距很近（几十公里内），因此用户与地面站的星历误差之差可以忽略，从而得到

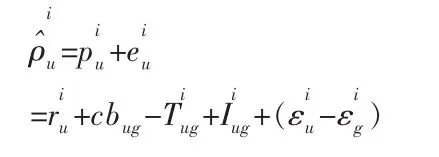
2 算法设计

2.1 差分算法思路

1）利用星历，计算当前时间点的卫星位置。

2）计算各个接收机的伪距差分修正量。

3）采用3.1.1中描述的算法对差分修正量进行融和处理。

4）利用处理后的差分修正量对伪距进行修正。

5）利用修正后的伪距进行差分定位。

接收机误差融和处理算法：

此算法的思想是利用不同信道产生的伪距差分来调整接收机的误差，具体做法为：假设对地面站存在M个无故障接收机和N颗可视卫星，令ρsc,i,j表示卫星i到接收机j视距上的伪距校正值。对于某一接收机到所有的卫星的观测量之中都含有同样的接收机钟差，因此，一个消除这种钟差的方法就是利用所有的伪距校正值估计该接收机钟差，并在改正值中减去该估计得到不含接收机钟差的伪距校正值ρsca,i,j从而再进行以下接收机之间的运算：

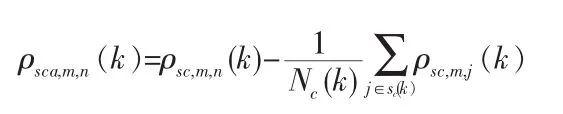
其中，sc代表最大可用的测距源个数

2.2 定位算法描述

定位算法采用的是最小二乘法迭代进行计算。

定位算法就是求解以下一个四元非线性方程组：

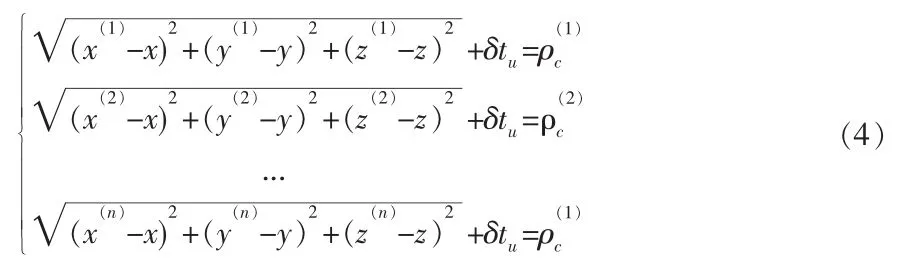
2.2.1 准备数据和设置初始解

设置当前位置坐标初始估计值为x0=计算差分修正后的伪距测量值 ρ（n）c-n为所有可见卫星。

2.2.2 非线性方程组线性化

接收机到卫星的几何距离：

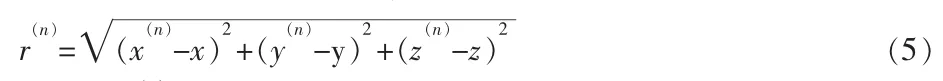
求函数 r（n）对 x 的偏导，得：

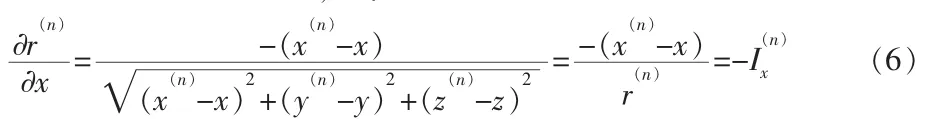
类似的对函数 r（n）对 y，z求偏导，即有：

2.2.3 求解线性方程组

套用最小二乘法的求解公式：

2.2.4 最后判断迭代的收敛性：计算位移向量 的长度：

3 数据实验验证

差分定位误差分析图如下：

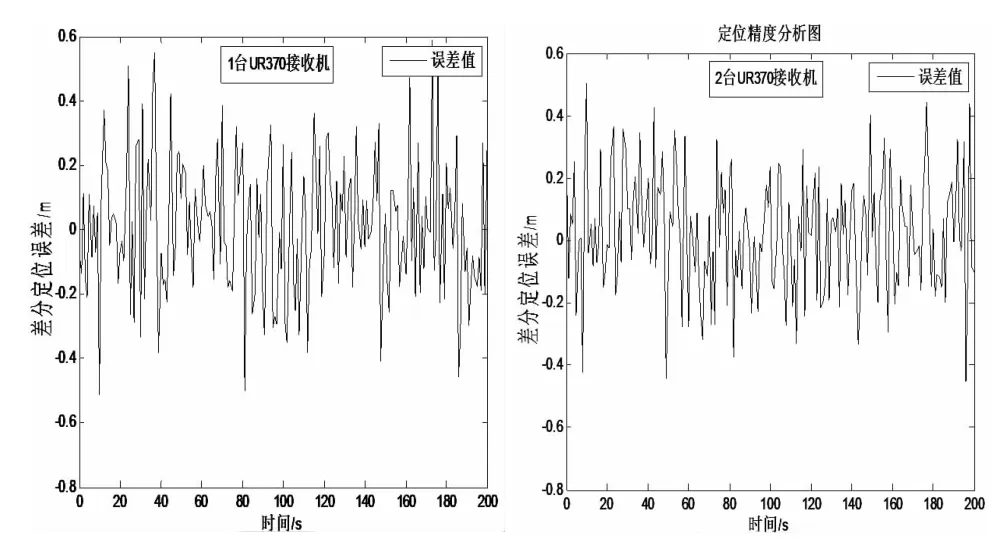
定位误差如下表所示：

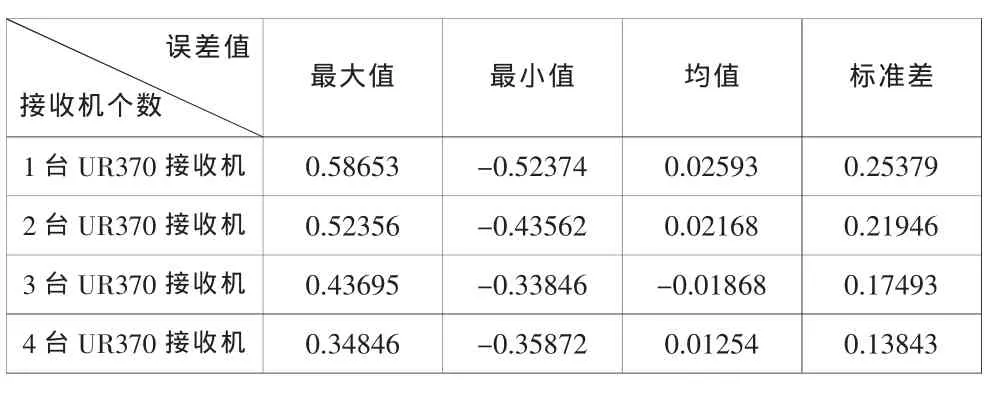
表1 差分定位误差结果分析

4 结论

本文通过实验数据测试结果可得定位误差与接收机个数相关，究其原因，在于多个接收机存在时，差分修正量在加权平均作用下，热噪声将会降低，而且当多个接收机工作时，系统可允许其中之一接收机故障，但不影响系统正常工作，增加了系统的稳定性。

［1］薛瑞.GBAS算法研究报告[D].北京：北京航空航天大学.

［2］谢刚.GPS原理与接收机设计[M].北京：电子工业出版社，2011,07.

［3］周忠谟，易杰军，周琪.GPS卫星测量原理与应用[M].北京：测绘出版社，1997.

［4］李庆扬，王能超，易大义.数值分析[J].北京：清华大学出版社，2001.

［5］刘经南，叶世榕.GPS非差相位精密单点定位技术探讨[J].武汉大学学报:信息科学版，2002（03）.