高速飞行器巡航飞行的姿态预测控制器设计

张天翼，周军，郭建国，王国庆

(1.西北工业大学精确制导与控制研究所，陕西西安710072;2.中国运载火箭技术研究院研究发展中心，北京100076)

0 引言

2010年，以超燃冲压发动机为动力的X-51A高超声速飞行器飞行试验［1］的进行，加快了世界高超声速飞行器的研究步伐，高超声速飞行器具有反应速度快、突防能力强、毁伤能力高等特点［2］。

预测控制理论是20世纪70年代出现在工业控制领域中的一类新型计算机控制算法。预测控制算法具有在不确定环境下进行优化控制的共性机理，其应用范围已延伸至航空航天领域。文献［3-4］中运用预测控制理论设计了飞行器的姿态控制器，仿真结果表明其具有良好的动态特性与鲁棒性。高超声速飞行器在巡航段的飞行时间较长，飞行器的飞行速度与飞行高度的变化相对缓慢，因此这为预测控制的应用提供了有利条件。本文针对高超声速飞行器巡航段的控制问题［5］，基于飞行器数学模型，设计了飞行器姿态预测控制器。

1 飞行器姿态控制模型

飞行器数学模型如下［6］:

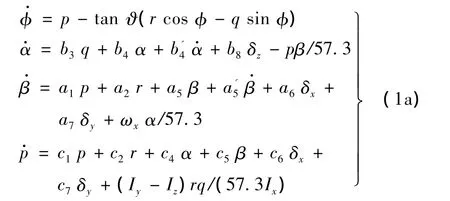
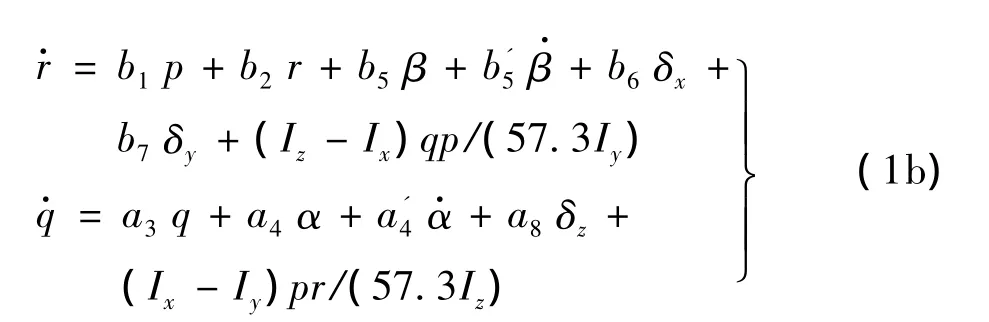
式中，相关参数定义见文献［6］。

以高超声速飞行器的俯仰通道为例，飞行器参考模型为［7］:

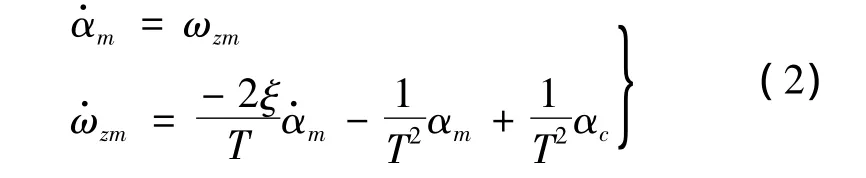
构造新的状态变量:

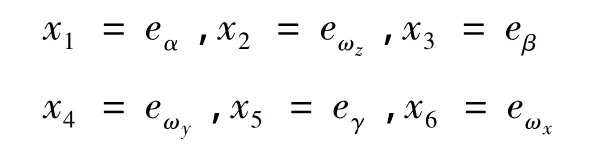
控制量 u=［δx，δy，δz］T，当系统存在参数摄动与干扰时，高超声速飞行器的姿态控制模型可化简为:

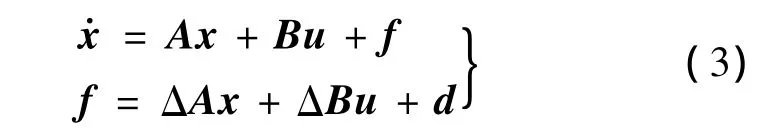
式中，ΔA，ΔB为飞行器气动参数的摄动;f为系统中的外界干扰。

2 飞行器姿态控制器设计

2.1 非线性干扰观测器设计

设非线性系统的状态方程为:

式中，x，d∈Rn;f(x)∈Rn;u∈Rm;G，H 为相应维数矩阵。非线性干扰观测器设计如下［8］:

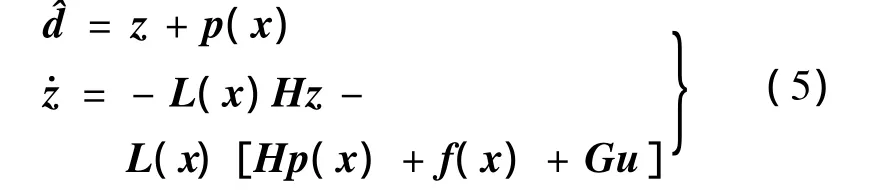
构造Lyapunov函数:

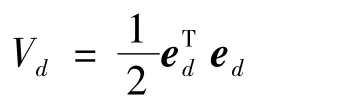
对函数Vd求导可得:

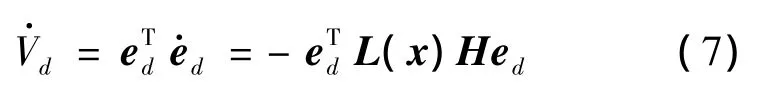
由式(7)可知，当满足L(x)H＞0条件时，干扰观测误差可全局稳定，因此可以根据H选择合适的p(x)，使得飞行器干扰观测器的观测误差全局稳定。

2.2 飞行器预测控制律设计

设有一小正数h＞0，函数fp(x)的表达式与预测值fp(x+h)如下所示:

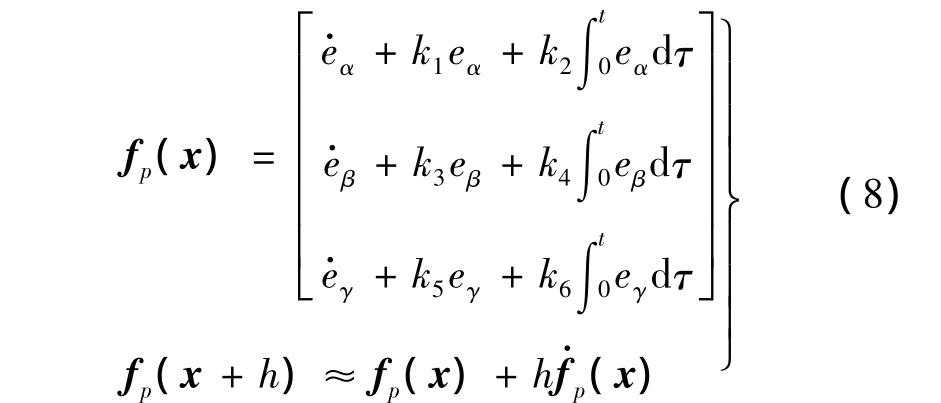
性能指标J设计为:

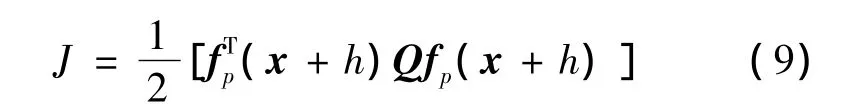
式中，Q为正定阵，其中:

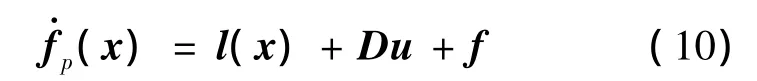
当性能指标J满足条件∂J/∂u=0时，控制律u为:

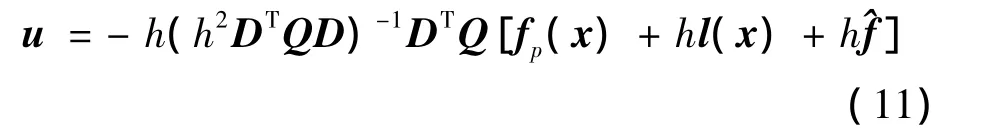
定理:在飞行器巡航段的飞行条件下，针对高超声速飞行器的姿态控制模型式(3)，假设飞行器外界干扰满足条件，飞行器在式(11)所描述的控制律u的控制作用下，系统的状态可渐近稳定。

证明:将控制律u代入式(10)中化简可得:

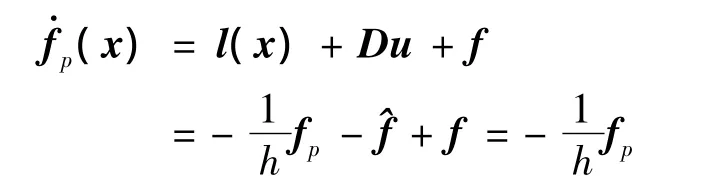
根据式(8)中函数fp的定义，以飞行器俯仰通道为例，可得关系式:

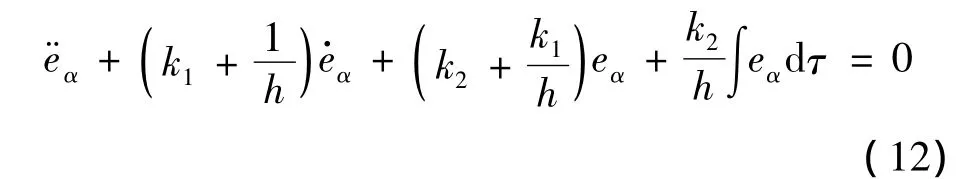
其中:

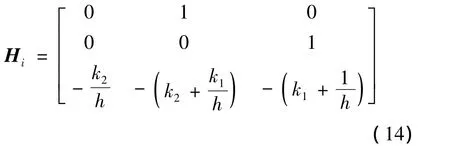
将飞行器三通道方程列写，则有状态方程:

其中:

同时定义非线性干扰观测器的观测误差为eob，则整个系统的状态扩张向量可定义为Σ =，定义 Lyapunov 函数:

式中，P=diag［Pi，I6×6］;Pi(i=1，2，3)满足 Riccati方程为正定对称矩阵，其最小特征值满足条件λ(Qi)min(i=1，2，3)=μ。对函数Vc求导可得:

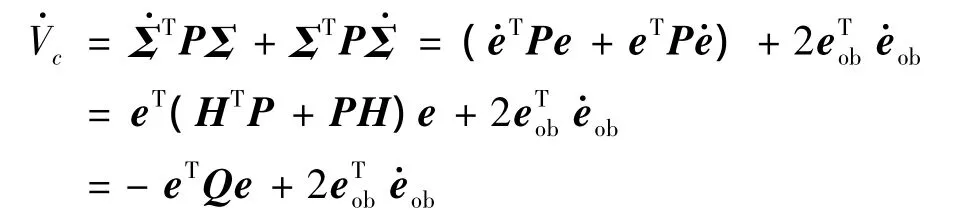
3 飞行器巡航段数字仿真

仿真的数学模型直接引用文献［6］中的结果，飞行器巡航段的飞行速度Ma=6，仿真时间100 s。同时考虑在气动参数标称、正向拉偏与负向拉偏三种情形下对飞行器巡航段进行仿真计算，其中气动力系数偏差±20%，气动力矩系数偏差±40%。

仿真中飞行器参考模型的时间常数T=0.3，阻尼系数ξ=0.7;飞行器预测控制器参数大小分别为:Q=diag［30，30，30］，k1=20，k2=100，k3=10，k4=25，k5=20，k6=40。飞行器非线性干扰观测器参数 p(x)与 L(x)分别设计为:p(x)=［10x1，10x2，10x3，10x4，10x5，10x6］T;L(x)=diag［10，10，10，10，10，10］。数字仿真结果分别如图1～图4所示。

由图1的仿真结果可以看出，飞行器迎角的动态响应在姿态控制器作用下可较好地适应飞行器气动参数的变化，迎角的变化范围可满足控制要求。

由图2和图3的仿真结果可以看出，飞行器侧滑角与滚转角的响应可稳定在0°附近，但由于飞行器三通道之间存在强烈的耦合作用，使得飞行器侧滑角与滚转角的响应均出现了微小的抖动，抖动的幅度大小可以稳定保持在0.2°以内。

由图4的仿真结果可以看出，飞行器在巡航段的飞行过程中，外界干扰(d)的变化较为缓慢，而应用非线性干扰观测器所获得的干扰观测值(d1)可稳定跟踪干扰真值的大小，由局部放大图也同时可以看出干扰观测值可由初值快速跟踪上真值的大小。

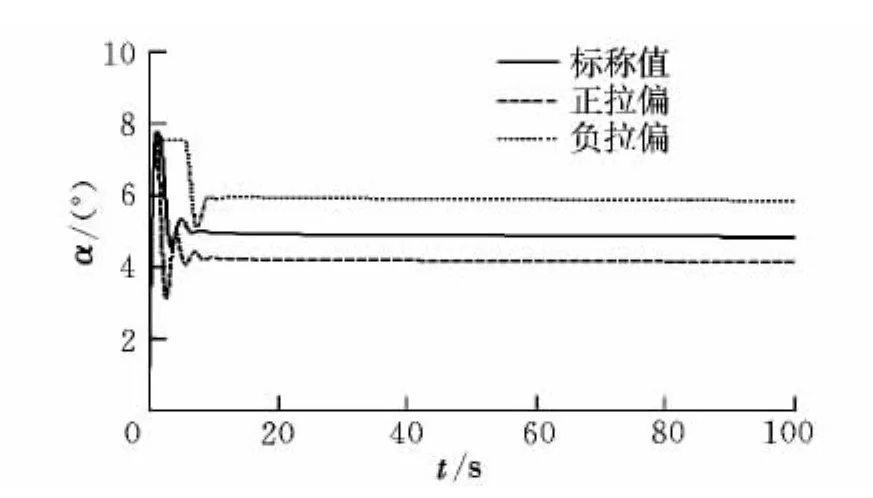
图1 飞行器迎角变化曲线Fig.1 Variation of AOA

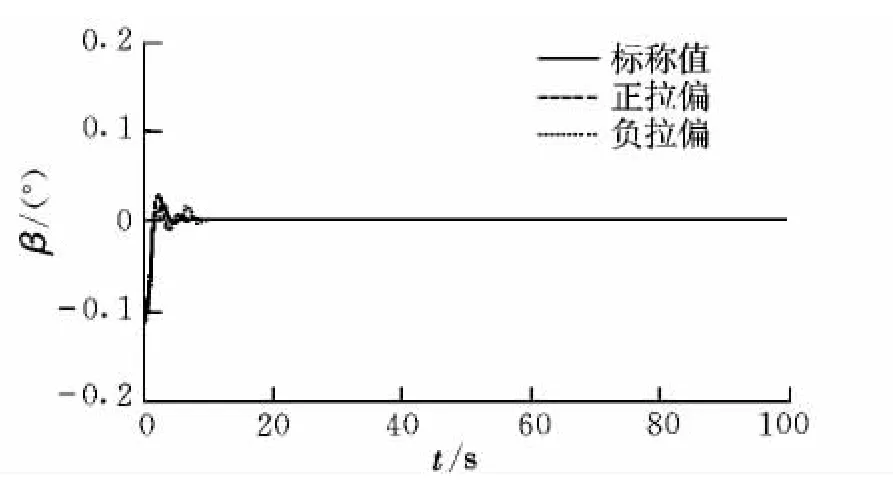
图2 飞行器侧滑角变化曲线Fig.2 Vehicle sideslip angle curve

图3 飞行器滚转角变化曲线Fig.3 Vehicle roll angle curve

图4 飞行器俯仰通道外界干扰变化曲线Fig.4 Variation of pitch channel under the external disturbance

综上所述可以看出，飞行器姿态角响应的性能指标均满足飞行器巡航段的控制要求，仿真结果也验证了本文控制方案设计的正确性。

4 结束语

针对高超声速飞行器巡航段的控制问题，提出了一种基于非线性干扰观测器的飞行器姿态预测控制器设计方法。将控制器用于高超声速飞行器巡航段的控制中，仿真结果表明，飞行器的姿态角均可实现稳定控制，控制器对于气动参数的摄动同时也具有较强的鲁棒性。

［1］ 刘冠男，周浩，陈万春.高超声速飞行器再入多段导引方法研究［J］.飞行力学，2012，30(4):337-340.

［2］ Tyler JV，Jonathan A M.A hypersonic vehicle model generator for MASIV［R］.AIAA-2012-4563，2012.

［3］ Tang W Q，Cai Y L.Predictive functional control:based missile autopilot design ［J］.Journal of Guidance，Control，and Dynamics，2012，35(5):1450-1455.

［4］ Frank F，Mark L.Model predictive control of agile projectiles［R］.AIAA-2012-4860，2012.

［5］ 朱纪立，刘向东，王亮，等.巡航段高超声速飞行器的高阶指数时变滑模飞行控制器设计［J］.宇航学报，2011，32(9):1945-1952.

［6］ 周凤岐，王延，周军.高超声速飞行器耦合系统变结构控制设计［J］.宇航学报，2011，32(1):66-71.

［7］ 周军.不确定性系统的变结构自适应控制理论及其应用［D］.西安:西北工业大学，1993.

［8］ 孙兆伟，邬树楠，李晖.带有干扰观测器的凝视航天器姿态变结构控制［J］.哈尔滨工业大学学报，2010，42(9):1374-1377.