欠驱动VTOL飞行器鲁棒动态面控制

袁瑞侠，刘金琨

(北京航空航天大学自动化科学与电气工程学院，北京100191)

0 引言

垂直起降飞行器(VTOL)的控制系统有三个自由度，因为两个控制输入的欠驱动为非最小相位系统，所以其控制系统的设计极具挑战性。

在过去的几十年里，根据不同的目标和侧重点，国内外学者有针对性地提出许多控制方法。早期VTOL飞行器控制［1-3］中忽略了输入滚转力和推力之间存在的耦合项，采用反馈线性化技术使系统稳定。但实际中耦合项并不能忽略，这种控制方法不能保证零动态是稳定的。文献［4］在考虑耦合项的情况下，通过反馈和坐标变换把参数不确定非线性系统近似为输入输出线性化系统，在此基础上设计的控制器可实现闭环系统的渐进稳定，且能把跟踪误差限制在一定范围内。但这种方法对于耦合项很大的情况仍不能得到很好的控制效果。文献［5］通过对状态变量进行坐标变换，使变换后的系统中不含有零动态，利用静态反馈很方便地实现了飞行器的稳定性和输入有界问题。文献［6］首先利用输入-输出线性化对VTOL系统全局坐标变换，然后对系统进行了分解，很方便地采用了滑模控制器，但只能保证闭环系统是局部稳定的。随着研究的深入，文献［7］中给出了VTOL飞行器镇定和轨迹跟踪的控制规范准则。

反演设计(Backstepping)为非匹配不确定非线性系统控制提供了一种有效的方法。文献［8］首先利用全局坐标变换使新系统符合下三角的形式，然后采用反演法完成控制律的设计，最后使飞行器可以全局渐进跟踪一个由参考模型产生的参考轨迹。然而，由于需要对非线性函数重复求导，反演设计得到的控制律复杂，这即是所谓的“微分爆炸”现象。另外，为了保证系统全局稳定性，Lyapunov函数和参数的选取条件较为苛刻。为了克服上述缺点，本文采用文献［8-9］提出的动态面控制(Dynamic Surface Control)，在反演设计的基础上引入一阶低通滤波器，使得每一步控制律设计与前一级设计基本解耦，从而使控制律的复杂程度大大下降，根本上避免了微分爆炸现象，在完成航迹跟踪的同时简化了Lyapunov函数的选取，并拓宽了控制律中参数的选取条件。

1 系统描述

利用机理分析法可建立VTOL动力学平衡方程为［1］:

式中，u1和u2为控制输入，即飞行器底部推力力矩和滚动力矩;g为重力加速度;ε0为描述u1和u2之间耦合关系的系数;Δ1(t)，Δ2(t)和Δ3(t)为外界干扰力矩，且对于正数 δ1，δ2，δ3满足 |Δ1(t)|≤δ1，

采用文献［5］中的全局坐标变换，可将控制系统变换为下三角结构的系统。另外，变换后的系统输出是平坦的，也就避免了原系统零动态不稳定的问题。令 z1=x1－ ε0sin θ，z2=x2－ ε0ω cos θ，w1=y1+ε0cos θ，w2=y2－ ε0ω sin θ，ξ1= θ，ξ2= ω，则变换后的系统为:

假设1:系统(2)中所有状态变量均可得到并用于反馈。

假设2:理想轨迹xd有界，其一阶、二阶导数存在并对正数χ1满足理想轨迹yd有界，其一阶、二阶导数存在并对正数χ2满足理想轨迹θd有界，其一阶、二阶导数存在并对正数χ3满足

2 动态面控制设计

仿照传统反演控制的“递进式”设计方法，自适应动态面控制的设计分为4步:

第1步:定义

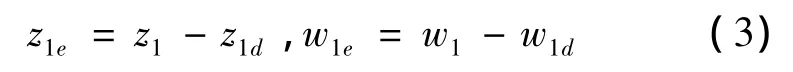
式中，z1d=x1d－ε0sin θd;w1d=y1d+ε0cos θd。设计虚拟控制:

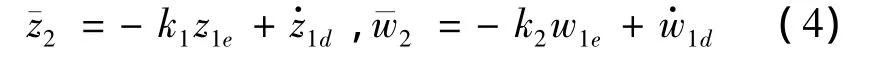
式中，k1，k2为待定正常数。

将¯z2，¯w2输入到如下时间常数为τ2z，τ2w的低通滤波器，得到新的状态变量z2d，w2d:

第2步:定义两个误差面为:

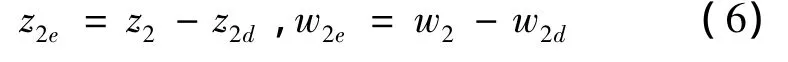
设计虚拟控制:

式中，k3，k4为待定正常数;和为非线性阻尼项，用于克服 Δ1(t)，Δ2(t)和 Δ3(t)。

解式(7)可设计虚拟控制为:

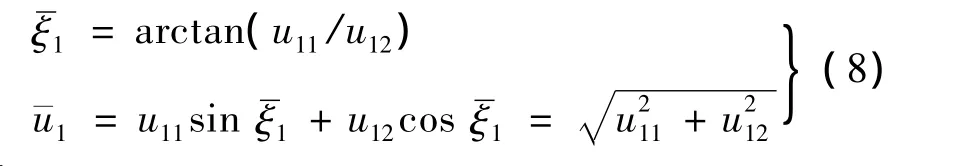
其中:

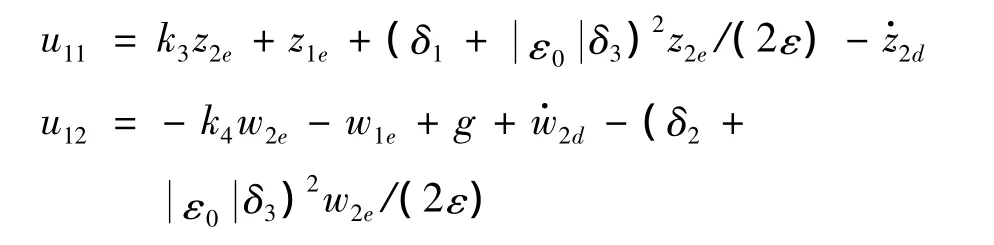
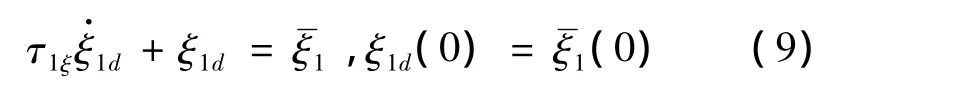
第3步:定义

设计虚拟控制:

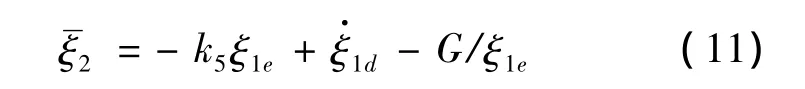
式中，k5为待定正常数。

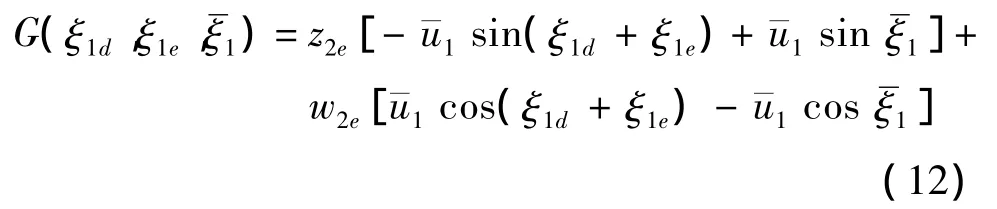
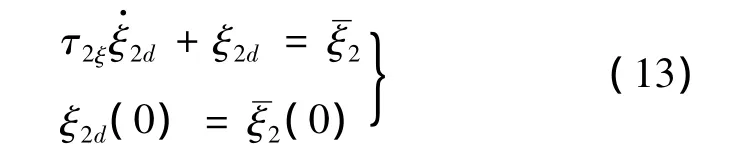
第4步:定义

设计控制律:

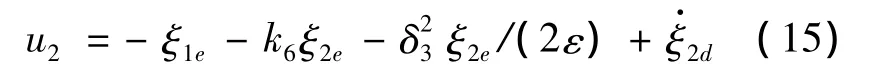
式中，k6为待定正常数为非线性阻尼项，用于克服干扰Δ3(t)。

3 稳定性分析

动态面控制器设计简单，但是由于引入低通滤波器，稳定性分析较为复杂。定义边界层误差为:

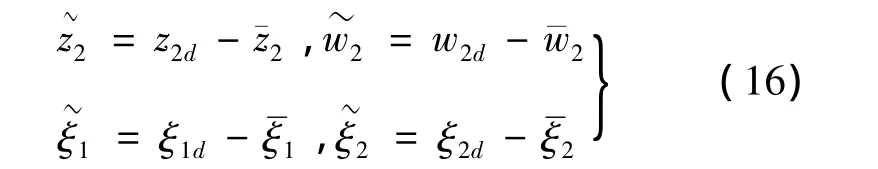
从式(5)、式(9)、式(13)得到:

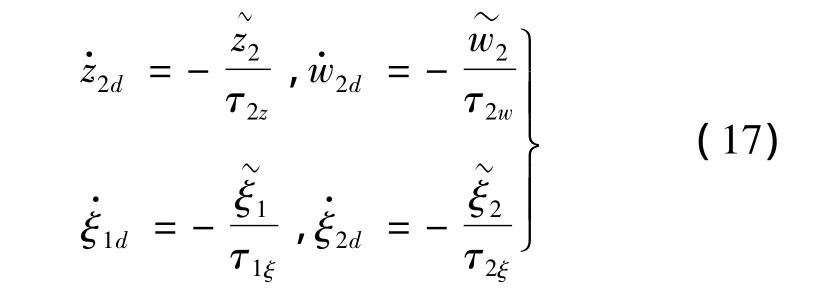
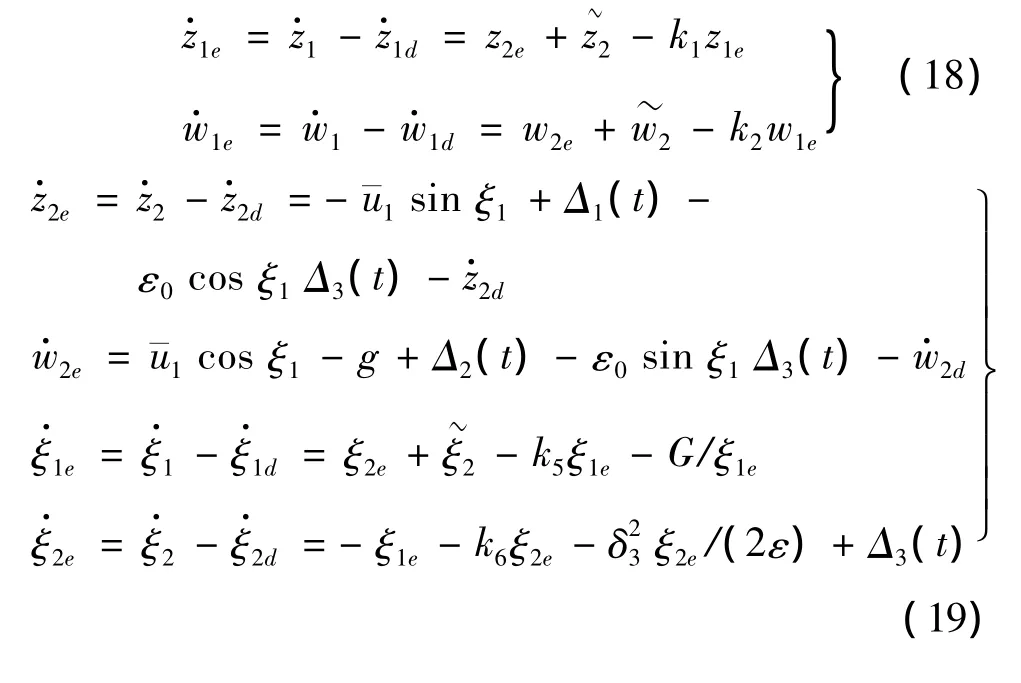
对边界层误差求导得到:

定义整个闭环系统的Lyapunov函数为:

其中:

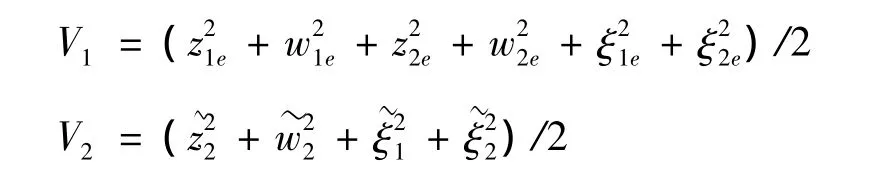
存在非负连续函数 B2z，B2w，B1ξ，B2ξ，使得:

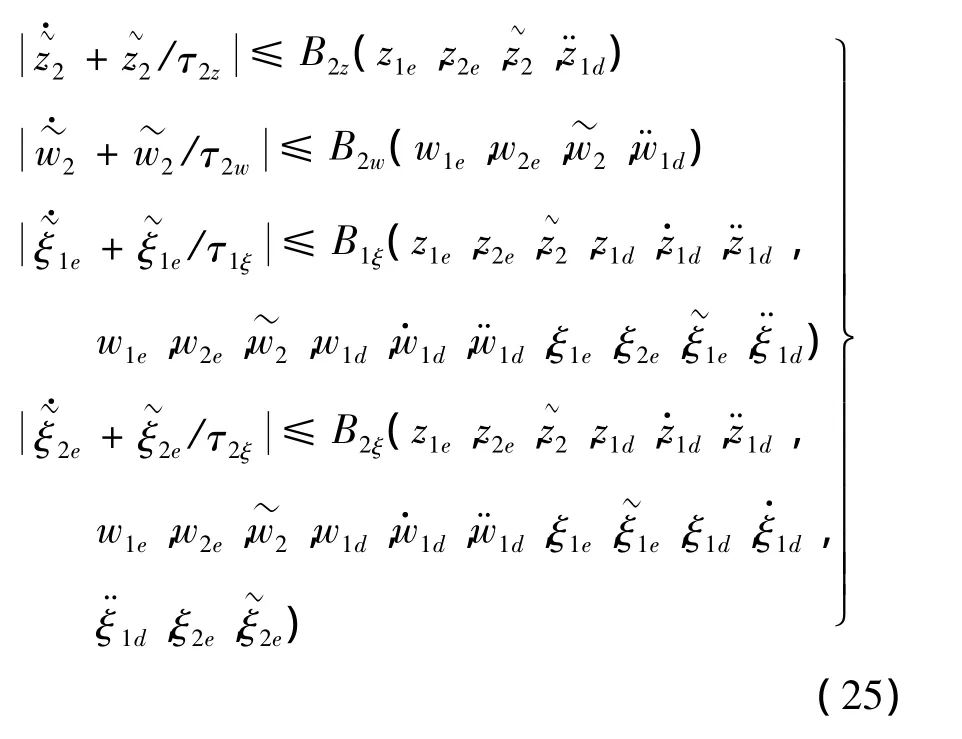
由式(25)容易得到如下不等式:

定理1:考虑由对象式(2)与实际控制器式(8)和式(15)组成的闭环系统，如果满足假设1和假设2并且初始条件满足V(0)≤p(p为任意正数)，则存在调节参数 ki(i=1，2，…，6)，τ2z，τ2w，τ1ξ，τ2ξ和ε，使得闭环系统所有信号半全局一致有界，系统跟踪误差可以收敛到任意小残集内。

证明:在V≤p成立的时刻，可考虑紧集:

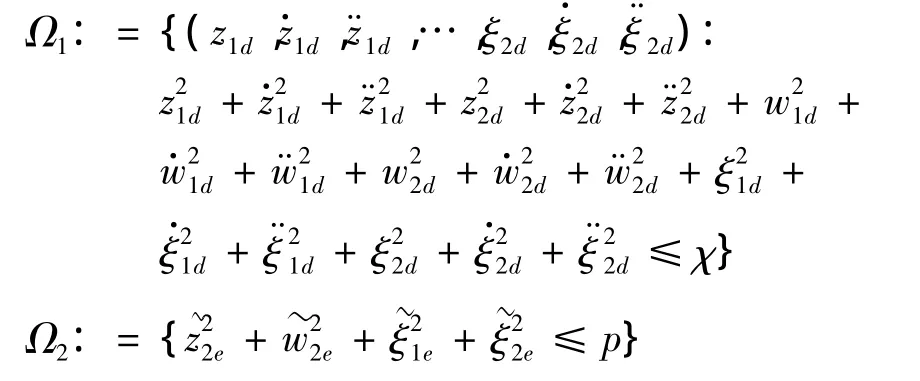
易知，此时Ω1×Ω2也是紧集。由此说明，在V≤p 成立时，B2z，B2w，B1ξ和 B2ξ在 Ω1× Ω2上有最大值，记为 M2z，M2w，M1ξ，M2ξ。

对V1求导，可得:

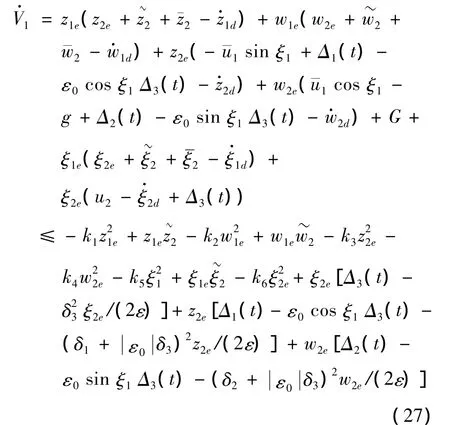
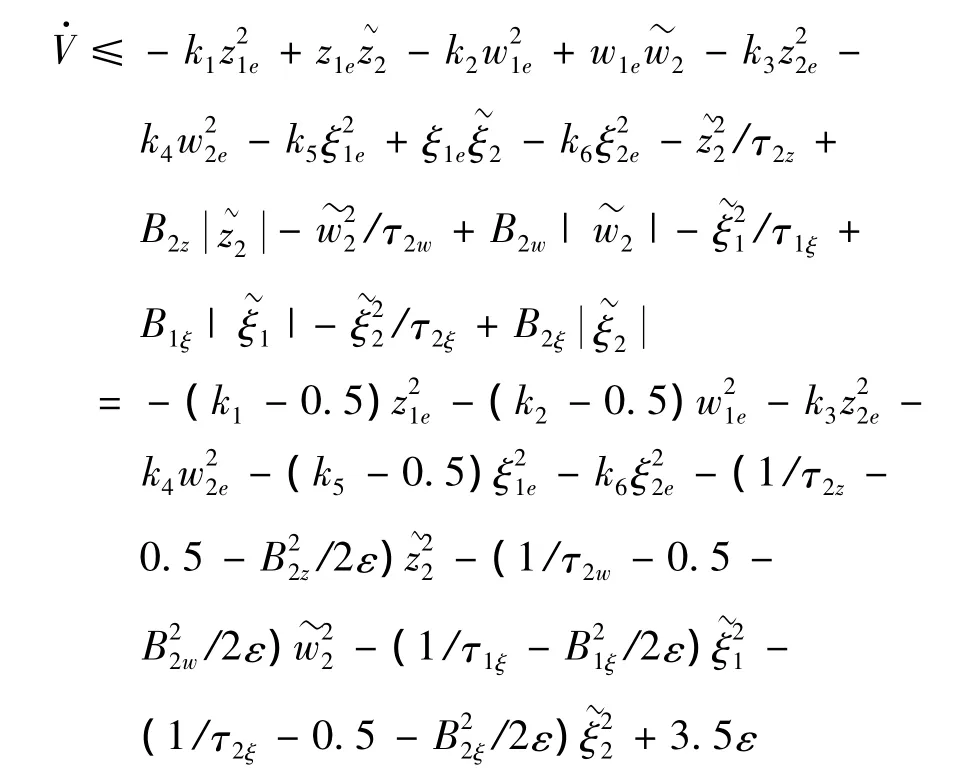
控制参数选取如下:

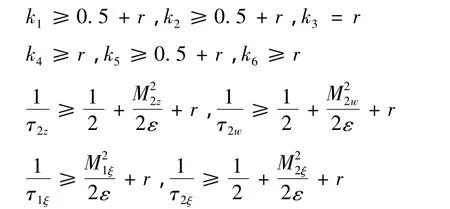
式中，r为待设计正数。则:

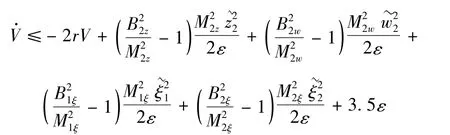
选取r≥3.5ε/(2p)。由于当 V=p时，Bi≤Mi成立，所以当 V=p时。由此可知V≤p是一个不变集，即如果V(0)≤p，则对所有t＞0均有V(t)≤p。由于有条件V(0)≤p，所以有:

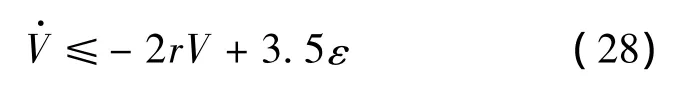
解上式得到:

显然，闭环系统所有信号半全局有界，并且有:

这意味着可以通过调节参数 ki(i=1，2，…，6)，B2z，B2w，B1ξ，B2ξ和 ε 使得 r任意大，即跟踪误差任意小。证明完毕。

4 仿真试验

仿真中，取动态面控制的参考航迹为x1d=3.5，y1d=4+cos t。假设外界干扰为 Δ1=0.1 sin t，Δ2=0.1 cos t和 Δ3=0.1 sin t，g 取9.8 m/s2。设定初始状态 x1(0)=5，x2(0)=0.1，y1(0)=3，y2(0)=0.2，φ(0)=0.1为了完成跟踪目标，根据在保证控制量大小合理的同时尽量减小跟踪误差的调参原则，取 ki=1(i=1，2，…，6)，τ2z= τzw= τ1ξ=τ2ξ=0.01，并取 ε =0.01。

仿真结果如图1～图4所示。

图1 横向跟踪效果图Fig.1 Lateral trajectory tracking effect

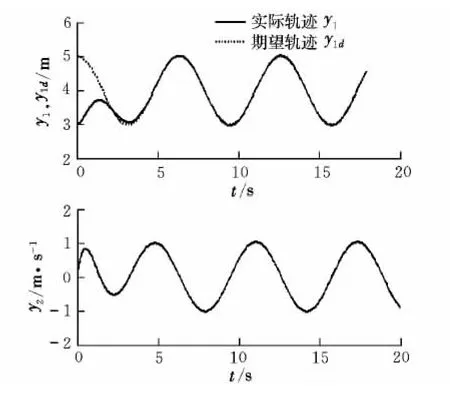
图2 垂向跟踪效果图Fig.2 Vertical trajectory tracking effect

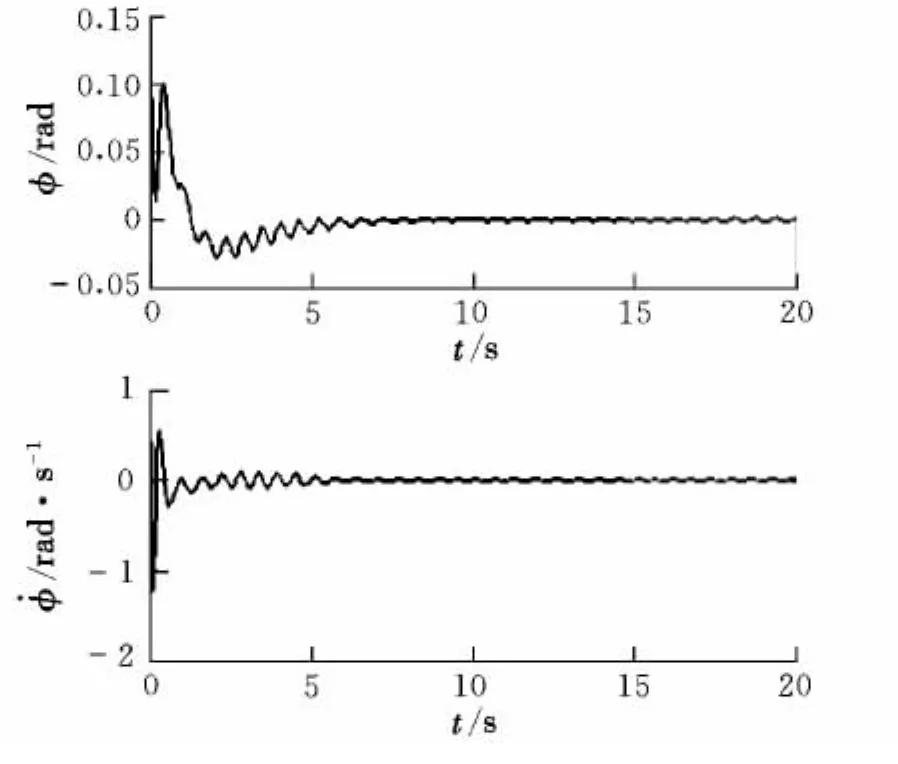
图3 滚转角及其角速度Fig.3 Roll angle and its angular speed

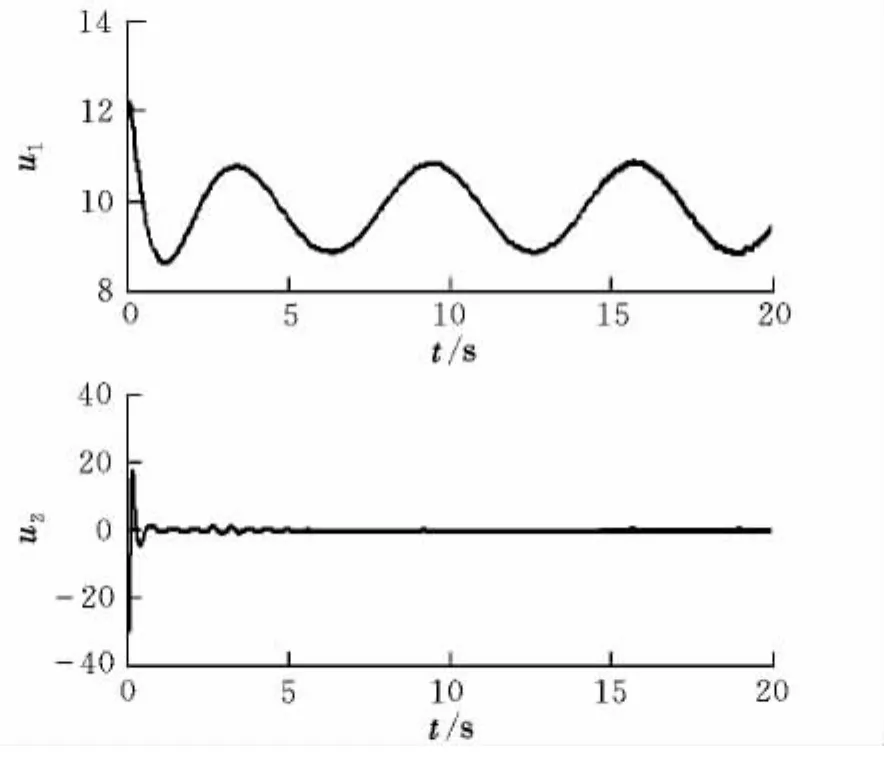
图4 控制输入Fig.4 Control input

由仿真结果可以看出，在控制输入的作用下，飞行器实际位置轨迹快速收敛于参考位置轨迹，且滚转角及其角速度是有界的。相比文献［8-9］中的Backstepping控制方法，证明闭环系统稳定性的Lyapunov函数的选取在简单的同时也降低了控制参数选取的难度。

5 结束语

针对带有外界干扰的VTOL飞行器系统，提出一种鲁棒动态面跟踪控制。通过引入低通滤波器避免了反复求导，消除了传统Backstepping方法存在的“微分爆炸”现象。通过引入非线性阻尼项克服了外界干扰，保证了系统的鲁棒性，满足实际工程要求。该策略能够保证闭环系统的半全局一致稳定，VTOL飞行器的位置信号能快速准确跟踪理想轨迹，同时保证滚转角有界。

［1］ Hauser J，Sastry S，Meyer G.Nonlinear control design for slightly non-minimum phase systems:application to V/STOL aircraft［J］.Automatic，1992，28(4):665-679.

［2］ Huang C S，Yuan K.Output tracking of a non-linear nonminimum phase PVTOL aircraft based on non-linear state feedback control［J］.International Journal of Control，2002，75(6):466-473.

［3］ Martin P，Devasia S，Paden B.A different look at output tracking:control of a VTOL aircraft［J］.Automatica，1996，32(1):101-107.

［4］ Ghanadan R，Blankenship G L.Adaptive approximate tracking and regulation of nonlinear systems［C］//Proceedings of the 32th IEEE Conference on Decision and Control.San Antonio，1993:2654-2659.

［5］ Olfati-Saber R.Global configuration stabilization for the VTOL aircraft with strong input coupling ［J］.IEEE Transactions on Automatic Control，2002，47(11):1949-1952.

［6］ Wang Xinhua，Liu Jinkun，Cai Kaiyuan.Tracking control for a velocity-sensorless VTOL aircraft with delayed outputs［J］.Automatica，2009，45(12):2876-2882.

［7］ Spanoudakis P，Tsourveloudis N C，Valavanis K P.Design specifications for an unmanned VTOL［C］//Proceedings of the 32th IEEE Conference on Robotics and Automation.New Orleans，2004:3616-3621.

［8］ Do K D，Jiang Z P，Pan J.On global tracking control of a VTOL aircraft without velocity measurements［J］.IEEE Transactions on Automatic Control，2003，48(12):2212-2217.

［9］ Zhu B，Wang X，Cai K Y.Tracking control for angularrate-sensorless vertical take-off and landing aircraft in the presence of angular-position measurement delay［J］.Control Theory and Applications，2010，4(6):957-969.