波尔共振仪实验的不确定度分析

全红娟，潘 渊，朱 婧，魏俊波，丁 健

(长安大学，陕西 西安 710064)

共振现象普遍存在于力学、电磁学、光学及分子、原子物理等物理学领域。共振虽然有时会给人们带来危害，但利用共振的特点也带来许多便利，如电磁共振、核磁共振等，所以有必要详细地了解共振现象。在高校实验教学中，波尔共振仪常用于研究摆轮的自由振动、阻尼振动和受近振动，用来巩固学生对机械振动理论部分知识的理解，笔者对该实验内容结果的测量不确度进行了讨论，并分析了影响结果的可能因素。

1 实验原理

当摆轮受到周期性策动力矩L=L0cosωt的作用，并在有空气阻尼和电磁阻尼的媒质中运动时(阻尼力矩为 －b，其运动方程为

式中:J是摆轮的转动惯量，－kθ为弹性力矩，L0为策动力矩的幅值，ω为策动力的圆频率。令ω20则式(1)变为

式(2)的通解为

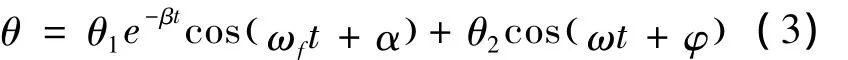
第一项表示减幅的阻尼振动;第二项表示与策动力频率相同的稳定的简谐振动。当第一项衰减为零后，受迫振动可以表示为:

解得振幅为

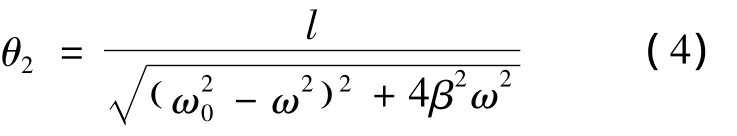
与策动力矩之间的相位差φ为

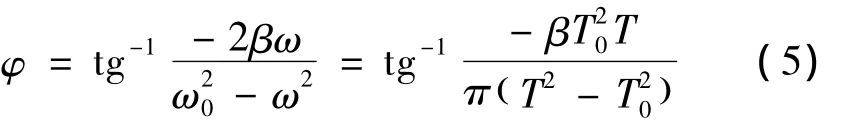
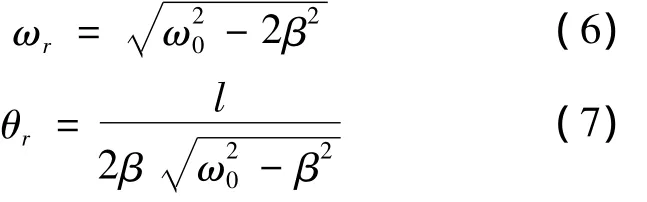
式(6)和式(7)表明，发生共振时频率ωr并不等于系统的固有频率ω0，而与系统的阻尼β有关。β越小，ωr越接近ω0，振幅θr也越大，图1表示出不同β时受迫振动的幅频特性和相频特性。

2 实验结果的测量不确度分析

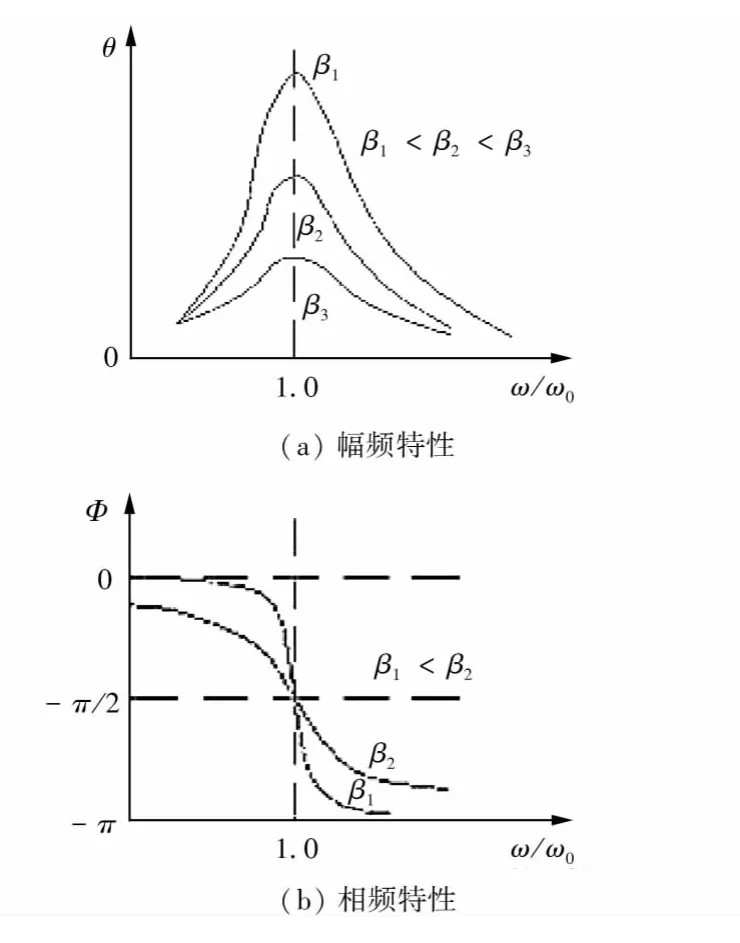
图1 受迫振动的幅频特性和相频特性

波尔共振实验仪可以进行自由振荡周期、阻尼系数和受迫振动幅频特性和相频特性的测量。下面将对自由振荡和阻尼振荡的测量结果，进行了不确定的分析，对于受迫振动，给出了幅频特性和相频特性的计算结果，见表1。

2.1 自由振荡

该模式下，阻尼档位为1，测量摆轮的固有频率。自由振荡通常认为是无阻尼状态，但实际上还会有空气阻尼、系统内部的耗散力等存在，正因为如此，表1中的测量数据(取16组测量结果的一部分)才会出现随着时间的推移，摆轮的振幅变小的现象。

表1 自由振荡下的摆轮周期和振幅的测量记录表

测量满足均匀分布，最小分辨力δx=0.001，则B类标准不确定度为

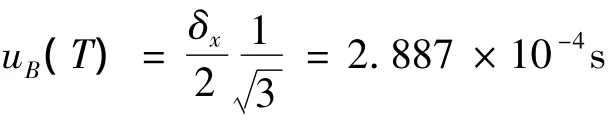
则合成标准不确定度为:

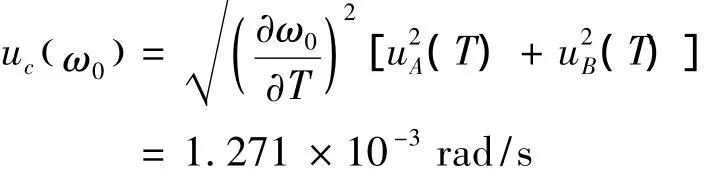
扩展不确定度为:

摆轮的固有频率为:

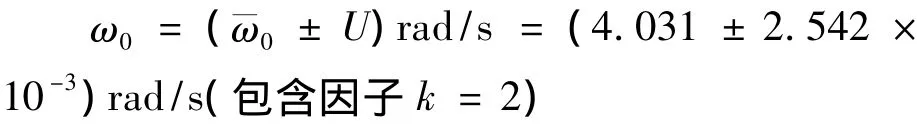
结果表明，摆轮的自由振荡频率真值以一定的概率落在了上面的区间内。

2.2 阻尼系数的测定

该模式下，阻尼档位为2，给摆轮的振动加上一定的电磁阻尼，这样实际振动总是受到阻力的影响，由于要克服阻力做功，摆轮的振幅逐渐减小。测量结果如表2所示(16组数据取11组)，这里采用逐差法处理数据。

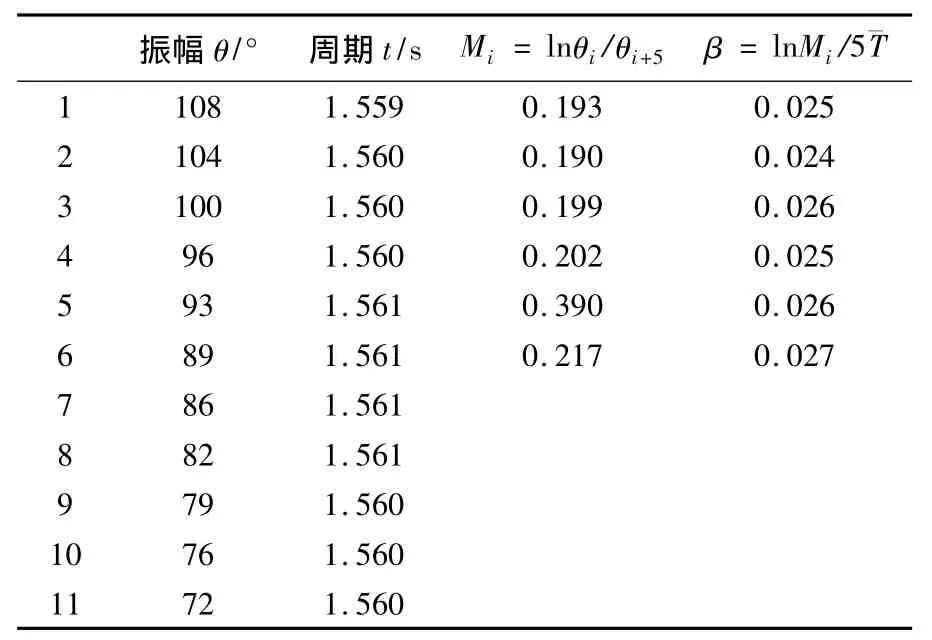
表2 阻尼振荡下的摆轮周期和振幅的测量记录表

可得周期¯T=1.560 s，¯M=1.241。阻尼系数¯β =0.028s－1。求得 A 类标准不确定度为测量满足均匀分布，最小分辨力δx=0.001，B类标准不确定度为

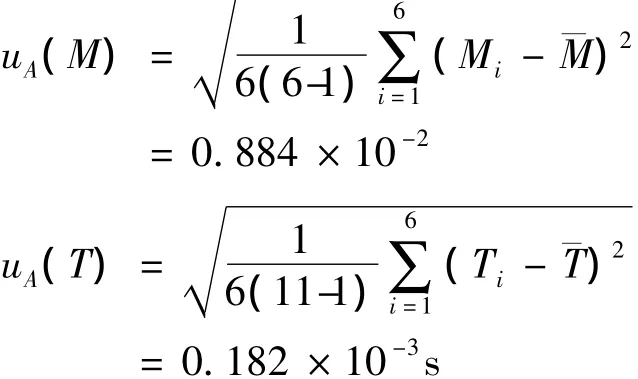
由β=ln M/5T，求得灵敏系数

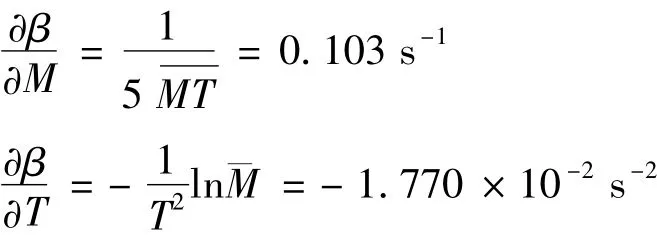
合成标准不确定度为

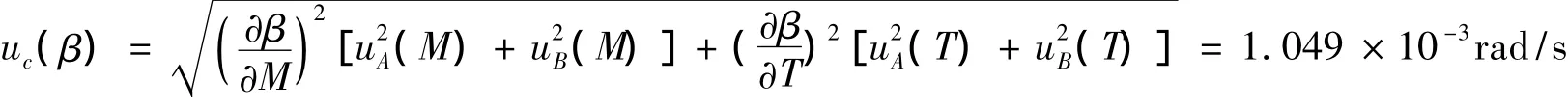
扩展标准不确定度为

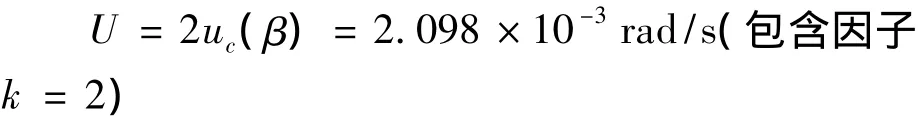
最终测量结果表达

结果表明，摆轮阻尼振荡的阻尼系数真值以一定的概率落在了上面的区间内。

2.3 受迫振动幅频特性和相频特性的测定

摆轮做受迫振动时的频率等于驱动力的频率，当驱动力的频率等于摆轮的固体频率时，摆轮振幅最大(共振)。该模式下，阻尼状态仍为2，测量数据如表3。

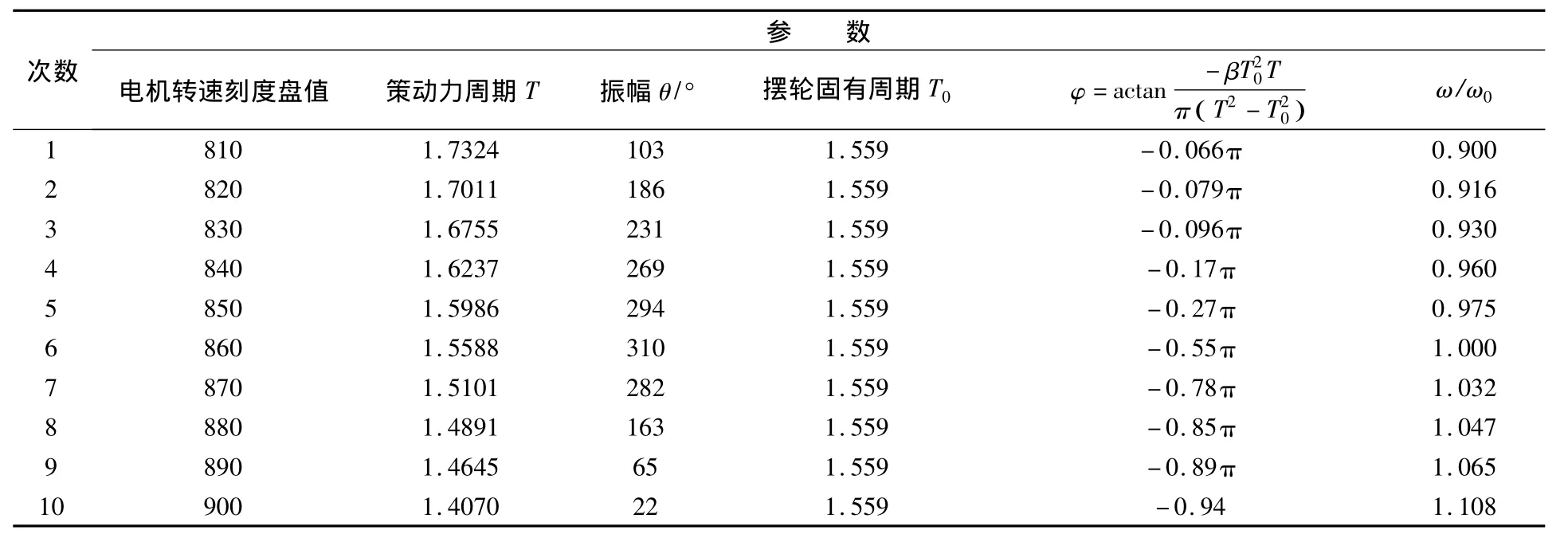
表3 摆轮做受迫振动的参数测量记录表

从表3的结果可以看出，摆轮做受迫振动的振幅由驱动力频率和物体的固有频率共同决定:两者越接近，受迫振动的振幅越大;两者相差越大，受迫振动的振幅越小。

3 影响测量结果的因素分析

实验过程中，由于轴承摩擦、弹簧非线性效应、电机转速不稳定的影响，受近振动的幅频特性测量常会出现扭摆不稳定的现象，导致有的测量数据会出现异常，所以需要完全领悟受迫振动的含义才能正确分析。在自由振动和阻尼振动的测量时，考虑到轴承的摩擦效应，摆轮的角度尽量介于120°～150°之间，才能保证阻尼系数基本为一个稳定值。此外，在实验操作中，尽量遵循“先定性观察，再定最测量”的原则，以使测量的结果更准确。

［1］董霖，王涵，朱洪波.波尔共振实验“异常现象”的研究［J］.大学物理，2010，29(2):57-60.

［2］李建设.波耳共振实验被测量相互验证技术研究［J］.新乡学院学报:自然科学版，2010，27(2):28-30.

［3］马学坤.线性受迫阻尼振动发生共振的条件及特征［J］.大学物理，2001，20(2):3-7.